31
2.1. Основные теоретические сведения
Критерии надежности резервированных невосстанавливаемых систем те же, что и нерезервированных невосстанавливаемых систем.
Основными видами резервирования являются: общее постоянное, общее замещением, раздельное постоянное, раздельное замещением. Структурные схемы резервированных систем приведены на рис. 2.1.
Рис. 2.1. Структурные схемы резервированных систем: общее резервирование с постоянно включенным резервом (а), раздельное резервирование с постоянно включенным резервом (б), общее резервирование замещением (в), раздельное резервирование замещением (г)
32
Приведем основные соотношения для показателей надежности резервированных сис-
тем.
2.1.1. Общее резервирование с постоянно включенным резервом
Пусть Pi(t) – вероятность безотказной работы i-го элемента за время t; Qi(t) – вероятность отказа i-го элемента за время t; f(t) – плотность распределения времени до отказа i-го элемента в момент времени t. Тогда вероятность безотказной работы, плотность распределения времени безотказной работы и интенсивность отказов системы с кратностью резервирования m определяется соотношениями:
|
T |
|||||||
|
Pc (t) =1−∏(1− Pi (t)), |
(2.1) |
||||||
|
i=0 |
|||||||
|
m |
|||||||
|
fc (t) = ∑(1− P0 (t))… fi (t)…(1− Pm (t)), |
(2.2) |
||||||
|
i=0 |
|||||||
|
m |
m |
||||||
|
∑ f j (t)∏Qi (t) |
|||||||
|
λ |
(t) |
= |
j=0 |
i≠ j |
. |
(2.3) |
|
|
c |
m |
||||||
|
1− |
∏Qi (t) |
i=0
В частности, для экспоненциальных распределений времени до отказа элементов с одинаковыми параметрами λ имеют место равенства:
|
P (t) =1−(1−e−λt )m+1 , |
|||||
|
c |
|||||
|
fc (t) = (m +1)λe−λt (1−e−λt )m , |
|||||
|
λc (t) = |
(m + |
1)λe−λt (1−e−λt )m |
. |
||
|
1 |
−(1−e−λt )m+1 |
||||
Среднее время безотказной работы системы определяется выражением:
|
1 |
m+1 |
1 |
|||
|
T1 = |
∑ |
. |
|||
|
λ k =1 |
k |
Формулы справедливы для случая, когда нерезервированная система рассматривается как один элемент, показатели надежности которого известны. В действительности любая система состоит из большого числа элементов, каждый из которых имеет показатель надежности, самостоятельно учитываемый при расчете. В таком случае формула для вероятности безотказной работы имеет вид:
|
m |
n |
|
|
Pc (t) =1−∏(1−∏Pij (t)) , |
(2.8) |
|
|
i=0 |
j=1 |
где n – число элементов нерезервированной системы, Pij(t) – вероятность безотказной работы элемента с номером (i,j).
2.1.2. Общее резервирование замещением
Вероятность безотказной работы, плотность распределения времени до отказа и среднее время безотказной работы системы определяются выражениями:
|
m |
|||
|
Pc (t) = P0 (t) + ∑ f0 f1 … fi−1 Pi (t), |
(2.9) |
||
|
i=1 |
|||
|
fc (t) = f0 |
f1 … fm (t). |
(2.10) |
|
|
Если все элементы равнонадежны, то: |
|||
|
m |
1 |
||
|
Pc (t) = ∑ f *(i ) P(t) =1− ∫ f *(m+1)(x)dx. |
(2.11) |
||
|
i=0 |
0 |
Формулы содержат свертки функций, обозначенные символом (*). Свертка функций f(t) и g(t), заданных при t ≥ 0, определяется соотношением:
33
|
f g(t) = ∫1 |
f (t − x)g(x)dx = ∫1 |
f (x)g(t − x)dx. |
(2.12) |
|
0 |
0 |
Выражение fc (t) = f0 f1 … fm (t).представляет собой i-кратную свертку функции f(t).
1442443
i
Если интенсивность отказов элементов постоянна и равна λ , то формулы для вероятности и среднего времени безотказной работы системы имеют вид:
|
m |
(λt) |
j |
|||
|
Pc (t) = ∑ |
e−λt , |
(2.13) |
|||
|
j! |
|||||
|
j=0 |
|||||
|
T = |
1 |
(m +1). |
(2.14) |
||
|
λ |
|||||
|
c |
2.1.3. Раздельное резервирование
Пусть исходная система состоит из т элементов. Тогда казной работы безотказной системы при раздельном резервировании выражаются следующими формулами:
– раздельное резервирование с постоянно включенным резервом:
|
n |
m |
||
|
Pc (t) = ∏(1−∏(1− Pij (t))), |
(2.15) |
||
|
j=1 |
i=0 |
||
|
– раздельное резервирование замещением: |
|||
|
n |
m |
||
|
Pc (t) = ∏∑ f0 j |
f1 j … fi−1, j Pij (t). |
(2.16) |
|
|
j=1 |
i=0 |
В формулах приняты следующие обозначения: Pij(t) – вероятность безотказной работы элемента с номером (i,j), fij(t) – плотность распределения времени до отказа элемента, i = 0,1, 2,…, m; j = 1, 2,…, n .
2.1.4. Резервирование с дробной кратностью
Приведем формулы для показателей надежности мажоритарных систем (систем с дробной кратностью резервирования), в которых n – общее число элементов, (n – m) основных и m резервных элементов. Отказ такой системы наступает при отказе (m + 1)-го элемента.
Показатели надежности мажоритарной системы при условии, что все элементы имеют одинаковую надежность, вычисляются по формулам:
|
m |
|||
|
Pc (t) = ∑Cni Qi (t)Pn−i (t), |
(2.17) |
||
|
i=0 |
|||
|
fc (t) = (n − m)CnmQm (t)Pn−m (t) f (t), |
(2.18) |
||
|
λc (t) = |
(n − m)CnmQm (t)Pn−m (t) |
λ(t). |
(2.19) |
|
m |
|||
|
∑Cni Qi (t)Pn−i (t) |
i=0
2.1.5. Скользящее резервирование
Скользящее резервирование представляет собой резервирование замещением с кратностью m/(n – m), где n – общее число элементов, m – число резервных элементов, (n – m) – число основных резервируемых элементов.
Вероятность безотказной работы системы со скользящим резервом при условии, что все элементы системы имеют одинаковую надежность, равна
|
m |
m |
|
|
Pc (t) = ∑ |
∑ f *(k1 ) P(t) f *(k2 ) P(t)… f *(kn−m ) P(t). |
(2.20) |
k =0 k1 +k2 +…+kn−m =k
Если элементы системы имеют экспоненциальное распределение вероятности времени до отказа с параметром λ , то вероятность безотказной работы, интенсивность отказов и среднее время безотказной работы системы соответственно равны:

Pc (t)
λc (t)
2.2. Примеры решения задач
34
|
m |
((n |
− m)λt) |
k |
|||||||
|
= ∑ |
e−(n−m)λt , |
|||||||||
|
k! |
||||||||||
|
k =0 |
||||||||||
|
((n − m)λt)m |
||||||||||
|
= (n − m)λ |
m! |
, |
||||||||
|
m |
k |
|||||||||
|
∑ |
((n − m)λt) |
|||||||||
|
k =0 |
k! |
|||||||||
|
T |
= |
m +1 |
T . |
|||||||
|
1c |
n − m |
1 |
Примеры и задачи для самостоятельного решения требуют использования компьютерных технологий. Применение универсальных математических программных средств позволит получить решение в короткое время без особого труда. В некоторых случаях решение удается получить в аналитическом виде. В примерах приводятся компьютерные технологии решения задач с применением систем Derive 5 и Excel. Отметим, что систему Derive 5 необходимо использовать всегда, где требуется получить решение в аналитическом виде.
Пример 2.1. Дана резервированная система с постоянным резервом кратности m = 2. Элементы системы имеют постоянную интенсивность отказа λ = 0,05 час-1. Найти показатели надежности системы: вероятность безотказной работы, плотность распределения времени до отказа, интенсивность отказа, среднее время безотказной работы.
Решение. Воспользуемся формулами (2.4)–(2.6). Тогда получим:
|
P (t) =1 |
−(1 |
−e−λt )m+1 =1−(1 |
−e−0.05t )3 , |
|||||||
|
c |
||||||||||
|
fc (t) = (m +1)λe−λt (1−e−λt )m |
= 3* 0.05λe−0.05t (1−e−0.05t )2 , |
|||||||||
|
λc (t) = |
(m +1)λe−λt (1−e−λt )m |
= |
1.15λe−0.05t (1−e−0.05t )2 |
= |
0.15(1−e−0.05t )2 |
. |
||||
|
1 |
−(1−e−λt )m+1 |
1−(1−e−0.05t )3 |
3 |
−3e−0.05t + e−0.1t |
||||||
Табулируя функции, найдем искомые показатели надежности, представленные в табл.
2.1.
Наиболее просто табулирование выполнить с помощью функции VECTOR системы Derive. Технология табулирования на экране монитора имеет вид:

f (t)
35
Пользователь вводит выражение вероятности безотказной работы (строка #1). Функции f(t) и λ (t) получены в соответствии с формулами:
f (t) = −P(t), λ(t) = P(t) .
Производная получена с помощью кнопки Find Derivative панели инструментов (строки #2 и #3). Интенсивность отказа (строка #4) получена в результате выполнения операции #3/#1. Функция табуляции представляется в следующем виде:
VECTOR([t,#1,#3,#4],t,0,100,5)
С помощью кнопки Sub панели инструментов вводятся исходные данные задачи. После щелчка мыши по кнопке Approximate на экране появиться решение в виде табл. 2.1.
Таблица 2.1
Показатели надежности резервированной системы с постоянно подключенным резервом и кратностью резервирования m = 2
|
t, час |
Рс(t) |
Fc(t) |
λ c(t) |
|
0 |
1 |
0 |
0 |
|
5 |
0,989177 |
0,005716 |
0,005778 |
|
10 |
0,939084 |
0,014085 |
0,014499 |
|
15 |
0,853108 |
0,19726 |
0,023122 |
|
20 |
0,747420 |
0,022049 |
0,029501 |
|
25 |
0,636777 |
0,021878 |
0,034357 |
|
30 |
0,531138 |
0,020200 |
0,038031 |
|
35 |
0,435977 |
0,017794 |
0,040814 |
|
40 |
0,353538 |
0,015177 |
0,042930 |
|
45 |
0,284042 |
0,012653 |
0,044546 |
|
50 |
0,226594 |
0,010374 |
0,045784 |
|
55 |
0,179785 |
0,008402 |
0,046736 |
|
60 |
0,142048 |
0,006743 |
0,047469 |
|
65 |
0,111871 |
0,005374 |
0,048036 |
|
70 |
0,087884 |
0,004260 |
0,048475 |
|
75 |
0,068907 |
0,003364 |
0,048815 |
|
80 |
0,053947 |
0,002648 |
0,049079 |
|
85 |
0,042185 |
0.002079 |
0,049283 |
|
90 |
0,032958 |
0.001630 |
0,049442 |
|
95 |
0,025731 |
0,001275 |
0,049566 |
|
100 |
0,020078 |
0,000997 |
0,049662 |
Графическая иллюстрация результатов дана на рис. 2.3. Согласно (2.7), среднее время безотказной работы системы будет равно:
|
1 |
m+1 |
1 |
1 |
1 |
|||||
|
T1c = |
∑ |
= 20(1+ |
+ |
) = 36,7 час. |
|||||
|
k |
2 |
3 |
|||||||
|
λ k =1 |
Пример 2.2. Требуется определить кратность резервирования системы с постоянным резервом, обеспечивающим вероятность безотказной работы 0,96 в течение времени t = 150 час. Элементы системы равнонадежны и имеют экспоненциальное распределение со средним временем безотказной работы T = 300 час. Найти также кратность резервирования для системы, элементы которой имеют распределение Рэлея с тем же средним.
Решение. Кратность резервирования может быть определена по формуле:
m= ln(1− Pc (t)) −1, ln(1− P (t))

36
где Р(t) – вероятность безотказной работы элемента в течение времени t, Pc(t) = 0,96 – вероятность безотказной работы системы в течение времени t.
Рис. 2.2. Вероятность безотказной работы
Рис. 2.3. Интенсивность и плотность распределения до отказа
Для экспоненциального распределения P1 (t) = e−λ1t ,
элемента.
Для распределения Рэлея P2 (t) = e−λ2t 2 , где λ2 = 4πT 2
В течение времени t = 150 час получим:
– для экспоненциального закона:
где λ1 = T1 – интенсивность отказа
– параметр распределения.
−1
P1 (t) = e−λ1t = e T = e0.5 = 0,606531;
– для закона Рэлея:
37
|
πt2 |
||||||||||
|
P (t) = e−λ2t 2 |
= e− |
= e |
π1502 |
= 0,821725. |
||||||
|
4T 2 |
||||||||||
|
e |
4 3002 |
|||||||||
|
Подставляя значения и P1(t), и Р2(t) в формулу для кратности резервирования т, полу- |
||||||||||
|
чим: |
||||||||||
|
– для экспоненциального распределения: |
||||||||||
|
m = |
ln(1−0,966) |
−1 = 2,45; |
||||||||
|
1 |
ln(1−0,606531) |
|||||||||
|
– для распределения Рэлея: |
ln(1−0,966) |
|||||||||
|
m2 |
= |
−1 = 0,87. |
||||||||
|
ln(1−0,821725) |
||||||||||
Округляя до целых чисел в большую сторону, получим m1 = 3, m2 = 1. Таким образом, для достижения заданной надежности в первом случае потребуется 3 резервных элемента, а во втором случае – только один.
Из примера видно, что надежность системы определяется не только ее структурой и временем работы, но также законом распределения времени до отказа элементов.
Пример 2.3. В условиях предыдущего примера необходимо обеспечить заданную надежность системы в течение времени t = 450 час. Решение.
Решение. Определим вероятность безотказной работы элемента в течение времени t = 450 час для экспоненциального распределения и распределения Рэлея:
|
−1 |
450 |
||||||||
|
P (t) = e−λ1t = e T |
= e |
300 |
= 0,22313; |
||||||
|
1 |
|||||||||
|
P (t) = e−λ2t2 = e− |
πt 2 |
π 4502 |
|||||||
|
4T 2 |
= e |
4*3002 |
= 0,17082. |
||||||
|
e |
|||||||||
|
Найдем кратность резервирования: |
|||||||||
|
– для экспоненциального распределения: |
|||||||||
|
m = |
ln(1−0,966) |
−1 =11,7; |
|||||||
|
1 |
ln(1−0,22313) |
||||||||
|
– для распределения Рэлея: |
ln(1−0,966) |
||||||||
|
m2 = |
−1 =16,2. |
||||||||
|
ln(1−0,17082) |
|||||||||
Округление до целых чисел дает требуемую кратность m1 = 12, m2 = 17. Если система работает время t = 450 час, то для достижения заданной надежности необходимо иметь 12 резервных элементов в первом случае и 17 резервных элементов во втором случае.
Из расчета следует, что структурное резервирование не может обеспечить вероятность безотказной работы системы 0,96 в течение 450 часов. Кратность резервирования настолько высока, что ее практическая реализуемость вряд ли возможна.
Пример 2.4. Структурная схема системы представляет собой дублированную систему с постоянно включенным резервом. Элементы системы имеют разные законы распределения времени до отказа: экспоненциальный с интенсивностью отказа λ = 2·10-3 час-1 и Вейбулла с параметрами α = 4, β = 500 час. Необходимо определить: вероятность безотказной работы
системы Pc(t), среднее время безотказной работы T1с, интенсивность отказов λ c(t). Решение получить в виде формул, таблиц и графиков.
Решение. В строках #1 и #2 представлены выражения вероятности безотказной работы системы при экспоненциальном законе распределения времени до отказа, а в строках #3 и #4
– при распределении Вейбулла (графическая интерпретация приведена на рис. 2.4). В строках #5 и #6 находятся выражения вероятности отказа и вероятности безотказной работы системы при общем резервировании с постоянно включенным резервом в виде следующих фор-
мул: Qc(t) = (1 – Pl(t))(1 – P2(t)), Pc(t) = l – Qc(t).

38
Встроке #7 находится производная от вероятности отказа системы, а в строке #8 – плотность распределения времени до отказа, полученная по формуле f(t) = Q′(t).
Врезультате интегрирования вероятности безотказной работы (строка #9) получено среднее время безотказной работы системы (строка #10), которое равно примерно 662 часам.
В строке #11 находится выражение для интенсивности отказа системы, полученное по формуле:
f (t)
λc (t) = Pc (t) .
c
Табулирование функции Pc(t) осуществлено в строке #12, а его результаты сведены в таблицу (строка #13).

39
На рис. 2.5 приведены зависимости от времени вероятностей безотказной работы элементов. Из графиков видно, что вероятность безотказной работы системы с законом распределения времени до отказа Вейбулла больше в области малых значений t и меньше при больших t.
Рис. 2.4. Вероятность безотказной работы элементов системы с законом распределения времени до отказа: экспоненциальным (кривая I ) и Вейбулла (кривая 2 )
Интересным, с точки зрения теории надежности, является график интенсивности отказов резервированной системы, построенный системой Derive по выражению #13 (рис. 2.5). Согласно теории интенсивность отказа резервированной системы при t = 0 равна нулю и с ростом t приближается к интенсивности отказа наиболее надежного элемента резервированной системы.
В нашем случае при больших t более надежной является система с экспоненциальным законом распределения времени до отказа, имеющей интенсивность отказа λ = 0,002 час-1. Из рис. 2.5 видно, что это условие идеально выполняется.
Рис. 2.5. Интенсивность отказа системы

40
Рис. 2.6. Вероятность безотказной работы при различной кратности резервирования
Пример 2.5. Дана резервированная система с постоянным резервом кратности m, все элементы которой равнонадежны и имеют усеченный нормальный закон распределения времени до отказа с параметрами m0 = 400 час и δ = 200 час. Определить все показатели надежности системы. Результаты представить в виде таблиц и графиков. Принять m = 0, 1, 2.
Решение. Для равнонадежных элементов формулы (2.1)–(2.3) показателей надежности принимают вид:
|
P (t) =1 |
−(1 |
−e−λt )m+1 , |
|||
|
c |
|||||
|
fc (t) = (m +1)λe−λt (1−e−λt )m , |
|||||
|
λc (t) = |
(m + |
1)λe−λt (1−e−λt )m |
. |
||
|
1 |
−(1−e−λt )m+1 |
||||
Плотность распределения времени до отказа и вероятность безотказной работы для усеченного нормального распределения равны соответственно:
|
(t −m |
)2 |
0.5 −Φ |
0 |
( |
t − m0 |
) |
||||||||||||||||
|
1 |
e− |
0 |
δ0 |
|||||||||||||||||||
|
f (t) = |
2δ0 |
, P(t) = |
, |
|||||||||||||||||||
|
δ |
0 |
2π (0.5 |
+ Φ |
0 |
( |
m0 |
)) |
0.5 + Φ |
0 |
( |
m0 |
) |
||||||||||
|
δ |
0 |
δ |
0 |
|||||||||||||||||||
где Ф0(t) – функция Лапласа. Для исходных данных задачи получим:
|
f (t) = |
1 |
e− |
2*200 |
2 |
, P(t) = |
0.5 −Φ0 ( |
t − 400 |
) . |
||
|
200 |
||||||||||
|
(t −400) |
||||||||||
|
200 |
2π (0.5 + Φ0 (2)) |
0.5 + Φ0 (2) |
Значения вероятности безотказной работы системы Pc(t) для кратности резервирования m = 0, 1, 2 содержатся в табл. 2.2. Соответствующие графики приведены на рис. 2.6.
Следует иметь в виду, что при больших значениях t вероятность безотказной работы настолько мала, что нет смысла эксплуатировать систему. Таблица необходима только для иллюстрации результатов решения задачи, представления решения в графическом виде и вычисления среднего времени безотказной работы системы методом Симпсона.
Из графиков следует, что Pc(t) возрастает при увеличении кратности резервирования, причем этот эффект тем сильнее, чем меньше m.
На основе данных табл. 2.2 приближенно вычислим среднее время безотказной работы системы для значений m = 0, 1, 2. Воспользуемся формулой Симпсона:

|
41 |
||||
|
h |
n−1 |
|||
|
T1 |
= |
(1+ ∑(3 + (−1)k )Pc (kh)), |
||
|
3 |
k =1 |
в которой шаг интегрирования примем равным h = 50 час, n = 20. Расчеты показывают, что
|
при m = 0 T1 ≈ 411час, при m = 1 T1 ≈ 518 час, при m = 2 |
T1 ≈ 573 час. |
|||||
|
Таблица 2.2 |
||||||
|
Вероятность безотказной работы резервированной системы |
||||||
|
t, час |
m = 0 |
m = 1 |
m = 2 |
|||
|
0 |
1,00000 |
1,00000 |
1,00000 |
|||
|
50 |
0,98229 |
0,99969 |
0.99999 |
|||
|
100 |
0,95492 |
0,99797 |
0,99991 |
|||
|
150 |
0,91517 |
0,99280 |
0,99939 |
|||
|
200 |
0,86093 |
0,98066 |
0,99731 |
|||
|
250 |
0,79138 |
0,95648 |
0,99092 |
|||
|
300 |
0.70756 |
0,91448 |
0,97499 |
|||
|
350 |
0,61264 |
0,84996 |
0,94188 |
|||
|
400 |
0,51164 |
0,76150 |
0,88353 |
|||
|
450 |
0,41064 |
0,65265 |
0,79528 |
|||
|
500 |
0,31572 |
0,53176 |
0.67959 |
|||
|
550 |
0,23190 |
0,41003 |
0,54684 |
|||
|
600 |
0,16235 |
0,29834 |
0,41225 |
|||
|
650 |
0,10811 |
0,20453 |
0,29053 |
|||
|
700 |
0,06836 |
0,13205 |
0,19139 |
|||
|
750 |
0,04099 |
0,08030 |
0,11800 |
|||
|
800 |
0,02328 |
0,04602 |
0,06823 |
|||
|
850 |
0,01251 |
0,02486 |
0,03706 |
|||
|
900 |
0,00635 |
0,01267 |
0,01894 |
|||
|
950 |
0,00305 |
0,00609 |
0,00912 |
|||
|
1000 |
0,00138 |
0,00276 |
0,00414 |
В табл. 2.3 содержатся значения плотности распределения вероятностей fс(t) для той же кратности резервирования. Графики fc(t) приведены на рис. 2.7.
Рис. 2.7. Плотность распределения времени до отказа при различной кратности резервирования

42
|
Таблица 2.3 |
|||
|
Плотность распределения времени до отказа |
|||
|
t, час |
m = 0 |
m = 1 |
m = 2 |
|
0 |
0,00028 |
0,00000 |
0,00000 |
|
50 |
0,00044 |
0,00002 |
0,00000 |
|
100 |
0,00066 |
0,00006 |
0,00000 |
|
150 |
0,00093 |
0,00016 |
0,00002 |
|
200 |
0,00154 |
0,00034 |
0,00007 |
|
250 |
0,00180 |
0,00064 |
0,00020 |
|
300 |
0,00198 |
0,00105 |
0,00046 |
|
350 |
0,00204 |
0,00153 |
0,00089 |
|
400 |
0,00198 |
0,00199 |
0,00146 |
|
450 |
0,00180 |
0.00233 |
0,00206 |
|
500 |
0,00154 |
0,00247 |
0,00253 |
|
550 |
0,00124 |
0,00237 |
0,00273 |
|
600 |
0,00093 |
0,00207 |
0,00261 |
|
650 |
0,00066 |
0,00167 |
0,00223 |
|
700 |
0,00044 |
0,00123 |
0,00173 |
|
750 |
0,00028 |
0,00085 |
0,00122 |
|
800 |
0,00016 |
0,00054 |
0,00079 |
|
850 |
0,00009 |
0,00032 |
0,00048 |
|
900 |
0,00005 |
0,00018 |
0,00027 |
|
950 |
0,00002 |
0,00009 |
0,00014 |
|
1000 |
0,00154 |
0,00005 |
0,00007 |
При m = 0 имеем график плотности усеченного нормального распределения времени до отказа основной системы. С увеличением кратности резервирования увеличивается среднее время безотказной работы и уменьшается дисперсия. Указанные факторы более ощутимы для системы с меньшей кратностью резервирования.
Интенсивности отказа системы для различных кратностей т имеют значения, приведенные в табл. 2.4. Соответствующие графики показаны на рис. 2.8.
Рис. 2.8. Интенсивность отказа системы при различной кратности резервирования
Из графиков следует, что большей кратности резервирования соответствует меньшая интенсивность отказов.

43
Таблица 2.4 Интенсивность отказа резервированной системы
|
t, час |
m = 0 |
m = 1 |
m = 2 |
|
0 |
0,00028 |
0,00002 |
0,00000 |
|
50 |
0,00045 |
0,00006 |
0,00000 |
|
100 |
0,00069 |
0,00016 |
0,00000 |
|
150 |
0,00102 |
0,00035 |
0,00000 |
|
200 |
0,00144 |
0,00067 |
0,00002 |
|
250 |
0,00195 |
0,00115 |
0,00007 |
|
300 |
0,00255 |
0,00180 |
0,00020 |
|
350 |
0,00323 |
0,00262 |
0,00047 |
|
400 |
0,00399 |
0,00357 |
0,00095 |
|
450 |
0,00482 |
0,00464 |
0,00165 |
|
500 |
0,00571 |
0,00577 |
0,00259 |
|
550 |
0,00664 |
0,00695 |
0,00372 |
|
600 |
0,00763 |
0,00815 |
0,00499 |
|
650 |
0,00864 |
0,00935 |
0,00632 |
|
700 |
0,00969 |
0,01054 |
0,00768 |
|
750 |
0,01077 |
0,01173 |
0,00902 |
|
800 |
0,01187 |
0,01290 |
0,01032 |
|
850 |
0.01298 |
0,01407 |
0,01159 |
|
900 |
0,01411 |
0,01524 |
0,01282 |
|
950 |
0,01526 |
0,01640 |
0,01402 |
|
1000 |
0,01641 |
0,00000 |
0,01521 |
Пример 2.6. Определить вероятность безотказной работы и плотность распределения времени до отказа мажоритарной системы, состоящей из n = 5 элементов с постоянной интенсивностью отказа λ = 0,004 час-1 при числе резервных элементов m = 1, 2, 3.
Решение. Для постоянной интенсивности отказов элементов P(t) = e−λt и Q(t) = 1 – e−λt . В соответствии с формулами (2.16) и (2.17) получим
m
Pc (t) = ∑Cn1 (1−e−λt )i e−λ(n−i)t , fc (t) = (n − m)λCn!m (1−e−λt )m e−λ(n−m)t . i=0n
Формула для Pc(t) представляет собой накопленные суммы биномиального распределе-
ния вероятностей с параметрами n = 5 и p = 1 – e−λt .
Вычисления по этим формулам в системе Derive настолько просто, что нет необходимости приводить здесь решение. Такие формулы также удобно программируются в Excel. В колонку А запишем значения t от 0 до 500 часов с шагом 20 часов. В ячейки В1 : F1 поместим кратность резервирования m. В ячейку В2 запишем формулу:
В2 = БИНОМРАСП(В$1;5;1–ЕХР(–0,004*$А2);1),
которую скопируем на остальные ячейки блока В2 : F27. В результате получим табл. 2.5. Таблица составлена при m = 0, 1, 2, 3, 4. Следует при этом иметь в виду, что при m = 0 и
m = 4 схема не является мажоритарной.
Графики Pc(t) при различном числе резервных элементов приведены на рис. 2.9 (номера кривых соответствуют числу резервных элементов). Из рисунка следует, что с ростом кратности резервирования надежность системы существенно увеличивается.
Плотность fс(t) без постоянного коэффициента (n – m) λ есть формула Бернулли для вычисления вероятностей биномиального распределения в зависимости от кратности резер-
вирования с параметрами n = 5 и р = 1 – e−λt . Поместим в колонку G время, а кратность резервирования в ячейки H1 : L1. В ячейку Н2 запишем формулу:
Н2 = (5–Н$1)*0,004*БИНОМРАСП(Н$1; 5; 1–ЕХР(–0,004*$А2); 0),

44
Таблица 2.5 Вероятность безотказной работы системы с дробной кратностью резервирования
|
A |
B |
C |
D |
E |
F |
|
|
1 |
t, час |
1 |
1 |
2 |
3 |
4 |
|
2 |
0 |
0,6703 |
1 |
1 |
1 |
1 |
|
3 |
20 |
0,4493 |
0,9495 |
0,9960 |
0,9998 |
1,0000 |
|
4 |
40 |
0,3012 |
0,8391 |
0,9744 |
0,9979 |
0,9999 |
|
5 |
60 |
0,2019 |
0,7097 |
0,9313 |
0,9914 |
0.9996 |
|
6 |
80 |
0,1353 |
0,5826 |
0,8697 |
0,9780 |
0,9985 |
|
7 |
100 |
0,0907 |
0,4681 |
0,7955 |
0,9565 |
0,9961 |
|
8 |
120 |
0,0608 |
0,3702 |
0,7145 |
0,9266 |
0,9919 |
|
9 |
140 |
0,0408 |
0,2891 |
0,6317 |
0,8890 |
0,9855 |
|
10 |
160 |
0,0273 |
0,2235 |
0,5511 |
0,8448 |
0,9764 |
|
11 |
180 |
0,0183 |
0,1714 |
0,4752 |
0,7955 |
0,9644 |
|
12 |
200 |
0,0123 |
0,1305 |
0,4056 |
0,7428 |
0,9494 |
|
13 |
220 |
0.0082 |
0,0989 |
0,3433 |
0,6881 |
0,9314 |
|
14 |
240 |
0.0055 |
0,0745 |
0,2883 |
0,6329 |
0,9105 |
|
15 |
260 |
0,0037 |
0,0560 |
0,2406 |
0,5782 |
0,8870 |
|
16 |
280 |
0,0025 |
0,0419 |
0,1995 |
0,5251 |
0,8612 |
|
17 |
300 |
0,0017 |
0,0312 |
0,1647 |
0,4742 |
0,8334 |
|
18 |
320 |
0,0011 |
0,0232 |
0,1353 |
0,4262 |
0,8039 |
|
19 |
340 |
0,0007 |
0,0172 |
0,1107 |
0,3812 |
0,7730 |
|
20 |
360 |
0,0005 |
0,0128 |
0,0902 |
0,3396 |
0,7413 |
|
21 |
380 |
0,0003 |
0,0094 |
0,0733 |
0,3014 |
0,7089 |
|
22 |
400 |
0,0002 |
0,0070 |
0,0594 |
0,2666 |
0,6762 |
|
23 |
420 |
0,0002 |
0,0051 |
0,0480 |
0,2351 |
0,6434 |
|
24 |
440 |
0,0001 |
0,0038 |
0,0387 |
0,2067 |
0,6109 |
|
25 |
460 |
0,0001 |
0,0028 |
0,0311 |
0,1813 |
0,5788 |
|
26 |
480 |
0,0000 |
0,0020 |
0,0250 |
0,1586 |
0,5474 |
|
27 |
500 |
1 |
0,0015 |
0,0200 |
0,1384 |
0,5167 |
Рис. 2.9. Вероятность безотказной работы мажоритарной системы

45
которую скопируем на остальные ячейки блока Н2 : L27. В результате получим табл. 2.6, которая содержит значения плотности fс(t) при различных m и t.
Табулирование функции fс(t) в системе Derive осуществляется с помощью Функции VECTOR, которая представляется в следующем виде:
VECTOR([t,fl(t),f2(t),f3(t),f4(t)],t,0,500,20).
Это наиболее простой способ представления решения в табличном виде. Графики плотностей изображены на рис. 2.10.
|
Таблица 2.6 |
||||||
|
Плотность распределения времени безотказной работы системы |
||||||
|
G |
H |
I |
J |
K |
L |
|
|
1 |
t, час |
0 |
1 |
2 |
3 |
4 |
|
2 |
0 |
0,02000 |
0,00000 |
0,00000 |
0,00000 |
0,00000 |
|
3 |
20 |
0,01341 |
0,00447 |
0,00056 |
0,00003 |
0,00000 |
|
4 |
40 |
0,00899 |
0,00624 |
0,00162 |
0,00019 |
0,00001 |
|
5 |
60 |
0,00602 |
0,00654 |
0,00266 |
0,00048 |
0,00003 |
|
6 |
80 |
0,00404 |
0,00609 |
0,00345 |
0,00087 |
0,00008 |
|
7 |
100 |
0,00271 |
0,00532 |
0,00393 |
0,00129 |
0,00016 |
|
8 |
120 |
0,00181 |
0,00447 |
0,00413 |
0,00170 |
0,00026 |
|
9 |
140 |
0.00122 |
0,00365 |
0,00411 |
0,00206 |
0,00039 |
|
10 |
160 |
0,00082 |
0,00292 |
0,00393 |
0,00235 |
0,00053 |
|
11 |
180 |
0,00055 |
0,00230 |
0,00365 |
0,00256 |
0,00068 |
|
12 |
200 |
0,00037 |
0,00180 |
0,00330 |
0,00270 |
0,00083 |
|
13 |
220 |
0,00025 |
0,00139 |
0,00293 |
0,00276 |
0,00097 |
|
14 |
240 |
0,00016 |
0,00106 |
0,00257 |
0,00276 |
0,00111 |
|
15 |
260 |
0,00011 |
0,00081 |
0,00222 |
0,00270 |
0,00124 |
|
16 |
280 |
0,00007 |
0,00061 |
0,00189 |
0,00260 |
0,00134 |
|
17 |
300 |
0,00005 |
0,00046 |
0,00160 |
0,00248 |
0,00144 |
|
18 |
320 |
0,00003 |
0,00035 |
0,00134 |
0,00233 |
0,00151 |
|
19 |
340 |
0,00002 |
0,00026 |
0.00112 |
0,00216 |
0,00157 |
|
20 |
360 |
0,00001 |
0,00019 |
0,00093 |
0,00200 |
0,00161 |
|
21 |
380 |
0,00001 |
0,00014 |
0,00077 |
0,00183 |
0,00163 |
|
22 |
400 |
0,00001 |
0,00011 |
0,00063 |
0,00166 |
0,00164 |
|
23 |
420 |
0,00000 |
0,00008 |
0,00051 |
0,00150 |
0,00163 |
|
24 |
440 |
0,00000 |
0,00006 |
0,00042 |
0,00134 |
0,00162 |
|
25 |
460 |
0,00000 |
0,00004 |
0,00034 |
0,00120 |
0,00159 |
|
26 |
480 |
0,00000 |
0,00003 |
0,00028 |
0,00107 |
0,00156 |
|
27 |
500 |
0,00000 |
0,00002 |
0,00022 |
0,00095 |
0,00151 |
Кривая 0 соответствует плотности распределения времени до отказа нерезервированной системы, состоящей из 5 элементов. Кривая 4 представляет собой плотность распределения времени до отказа резервированной системы с одним основным и четырьмя резервными элементами.
Пример 2.7. Дана резервированная система с резервом замещением кратности m = 2. Элементы системы имеют постоянную интенсивность отказа , λ = 0,05 час-1. Определить вероятность безотказной работы и среднее время безотказной работы системы. Сравнить Pc(t) с постоянно включенным резервом.
Решение. По формуле (2.13) получим:
Pc (t) = (λtj!) j e−λt = (1+ λt + (λ2t)2 )e−λt .

46
Рис. 2.10. Плотность распределения времени безотказной работы мажоритарной системы
Рассчитанные Pc(t) при различных значениях t сведены в табл. 2.7. Для сравнения в таблицу помещены также значения Pc(t) для постоянно включенного резерва.
График вероятности безотказной работы для обоих видов резервирования оказан на рис. 2.11.
Среднее время безотказной работы для резерва замещением по формуле (2.11) равно T1c = 3T1c = 3·20 = 60 час. Для постоянного резерва, как было показано в примере 2.1, это время составляет 36,7 часа.
Таблица 2.7 Вероятность безотказной работы системы при различных видах резервирования
|
t, час |
Резерв замещением |
Постоянный резерв |
|
0 |
1 |
1 |
|
10 |
0,985612 |
0,939084 |
|
20 |
0.919699 |
0,74742 |
|
30 |
0,808847 |
0,531138 |
|
40 |
0,676676 |
0,353538 |
|
50 |
0,543813 |
0,226594 |
|
60 |
0,42319 |
0,142048 |
|
70 |
0,320847 |
0,087884 |
|
80 |
0,238103 |
0,053947 |
|
90 |
0,173578 |
0,032958 |
|
100 |
0,124652 |
0,020078 |
|
110 |
0,088376 |
0,01221 |
|
120 |
0,061969 |
0,007418 |
|
130 |
0,043036 |
0,004504 |
|
140 |
0,029636 |
0,002733 |
|
150 |
0,020257 |
0.001658 |
|
160 |
0,013754 |
0,001006 |
|
170 |
0,009283 |
0,00061 |
|
180 |
0,006232 |
0,00037 |

47
Рис. 2.11. Вероятность безотказной работы для резерва замещением (кривая 1) и для постоянно включенного резерва (кривая 2)
Пример 2.8. Даны 3 системы с кратностями резервирования m = 0, 2, 4 (резерв замещением). Элементы системы равнонадежны и имеют гаммараспределение времени до отказа с параметрами α = 3, β =100 часам. Определить показатели надежности систем: вероятность
безотказной работы, плотность и среднее время безотказной работы. Привести таблицы и графики.
Общее число элементов в системах равно n = 1, 3, 5 соответственно.
Решение. Воспользуемся формулами (2.10)–(2.12). Если f(t) – плотность гаммараспределения с параметрами α и β , то n-кратная свертка f*(n)(t) также имеет гамма-
распределение с параметрами nα и β . Поэтому плотность распределения времени до отказа и вероятность безотказной работы выражаются равенствами:
|
t nαa−1 |
e− |
1 |
, |
||||||
|
fc (t) = f *(n) (t) = |
β |
||||||||
|
β nα Γ(nα) |
|||||||||
|
− t |
t nαa−1 |
e− |
x |
||||||
|
P (t) =1 |
β |
dx. |
|||||||
|
c |
∫0 |
β nα Γ(nα) |
|||||||
Плотность и функция гамма-распределения легко вычисляются в Excel. Для этого на листе Excel в графе А поместим время t, изменяющееся от О До 2000 часов с шагом 100 часов. Вторую строку таблицы заполним формулами:
В2 = ГАММАРАСП(А2;1*3;100;0), С2 = ГАММАРАСП(А2;3*3;100;0), 02 = ГАММАРАСП(А2;5*3;100;0),
Е2 = 1 – ГАММАРАСП($А2;1*3;100;1), F2 = 1 – ГАММАРАСП($А2;3*3;100;1), G2 = 1 – ГАММАРАСП($А2;5*3;100;1).
В ячейках В2 : D2 содержатся значения плотности гамма-распределения (последний аргумент равен 0) с параметром формы, соответствующим числу элементов 1, 3, 5. В ячейках Е2: G2 содержатся значения функции гаммараспределения (последний аргумент равен 1) с такими же параметрами формы.
Копируя эти формулы на блок ячеек ВЗ : G22, получим табл. 2.8.

48
Таблица 2.8 Плотность и вероятность безотказной работы для различной кратности резервирования
|
A |
B |
C |
D |
E |
F |
G |
|
|
1 |
t |
f(t), m = 0 |
f(t), m = 2 |
f(t), m = 4 |
P(t), m = 0 |
P(t), m = 2 |
P(t), m = 4 |
|
2 |
0 |
0 |
0 |
0 |
1 |
1 |
I |
|
3 |
100 |
0,00184 |
0,00000 |
0,00000 |
0,9197 |
1,0000 |
1,0000 |
|
4 |
200 |
0,00271 |
0,00001 |
0,00000 |
0,6767 |
0,9998 |
1,0000 |
|
5 |
300 |
0,00224 |
0,00008 |
0,00000 |
0,4232 |
0,9962 |
1,0000 |
|
6 |
400 |
0,00147 |
0,00030 |
0,00000 |
0,2381 |
0,9786 |
1,0000 |
|
7 |
500 |
0,00084 |
0,00065 |
0,00000 |
0,1247 |
0,9319 |
0,9998 |
|
8 |
600 |
0,00045 |
0,00103 |
0,00002 |
0,0620 |
0,8472 |
0,9986 |
|
9 |
700 |
0,00022 |
0,00130 |
0,00007 |
0,0296 |
0,7291 |
0,9943 |
|
10 |
800 |
0,00011 |
0,00140 |
0,00017 |
0,0138 |
0,5925 |
0,9827 |
|
11 |
900 |
0,00005 |
0,00132 |
0,00032 |
0,0062 |
0,4557 |
0,9585 |
|
12 |
1000 |
0,00002 |
0,00113 |
0,00052 |
0,0028 |
0,3328 |
0,9165 |
|
13 |
1100 |
0,00001 |
0,00089 |
0,00073 |
0,0012 |
0,2320 |
0,8540 |
|
14 |
1200 |
0,00000 |
0,00066 |
0,00090 |
0,0005 |
0,1550 |
0,7720 |
|
15 |
1300 |
0,00000 |
0,00046 |
0,00102 |
0,0002 |
0,0998 |
0,6751 |
|
16 |
1400 |
0.00000 |
0,00030 |
0,00106 |
0,0001 |
0,0621 |
0,5704 |
|
17 |
1500 |
0,00000 |
0,00019 |
0,00102 |
0.0000 |
0,0374 |
0,4657 |
|
18 |
1600 |
0,00000 |
0,00012 |
0,00093 |
0,0000 |
0,0220 |
0,3675 |
|
19 |
1700 |
0,00000 |
0,00007 |
0,00080 |
0,0000 |
0,0126 |
0,2808 |
|
20 |
1800 |
0,00000 |
0,00004 |
0,00065 |
0,0000 |
0,0071 |
0,2081 |
|
21 |
1900 |
0,00000 |
0,00002 |
0,00051 |
0,0000 |
0,0039 |
0,1497 |
|
22 |
2000 |
0,00000 |
0,00001 |
0,00039 |
0,0000 |
0,0021 |
0,1049 |
По колонкам Е, F, G таблицы можно построить графики вероятности безотказной работы для кратностей резервирования m = 0, 2, 4 (рис. 2.12).
Рис. 2.12. Вероятность безотказной работы системы с резервом замещением
По колонкам В, С, D можно построить графики плотности распределения времени безотказной работы для тех же кратностей резервирования (рис. 2.13).
Среднее время безотказной работы резервированной системы вычислим по формуле (2.11): T1c = nT1, где T1 = αβ = 300 час – среднее время безотказной работы одного элемента.

49
Для системы с заданными кратностями резервирования соответственно получим T1c = T1 = 300 час, T1с = 3T1 = 900 час, T1c = 5T1 = 1500 час.
Рис. 2.13. Плотность распределения времени до отказа системы с резервом замещением
Пример 2.9. Вычислить среднее время безотказной работы системы при общем резервировании с постоянно включенным резервом и нормальном законе распределения времени до отказа нерезервированной системы.
Решение получить в аналитическом виде и в виде таблицы при следующих значениях исходных данных: кратность резервирования k = 1…10, параметры нормального закона распределения m = 100, δ = 20.
Решение. Далее приведена технология решения задачи в системе Derive (см. ниже).

50
В строках #1 и #2 определены области изменения переменных. В строке #3 приводится выражение плотности нормального закона распределения времени до отказа. Интеграл (строка #4) от плотности является вероятностью отказа системы (строка #5). В строке #6 определяется выражение вероятности безотказной работы резервированной системы с кратностью k. В строках #7 и #8 находятся выражения среднего времени безотказной работы резервированной системы. Табулирование функции осуществлено с помощью функции VECTOR (строка #9), а ее результаты приведены в строке #10.
Пример 2.10. Дана резервированная система со скользящим резервом, состоящая из 4-х элементов: два основных и два резервных (n = 4, m = 2). Время безотказной работы каждого элемента имеет нормальное распределение с математическим ожиданием Т = 500 час и средним квадратическим отклонением δ = 100 час. Найти вероятность безотказной работы, аналогичным показателем для экспоненциального распределения.
Решение. Раскрывая формулу (2.19) при n = 4, m = 2, получим
Рс(е) = Р2(t) + 2f *P(t)P(t) + 2f*(2)*Р(t)P(t)+ (f*P(t))2 ,
где P(t) – вероятность безотказной работы, а f(t) – плотность распределения времени до отказа одного элемента. Поскольку сумма к независимых нормально величин имеет нор-
мальное распределение с параметрами kT и 
|
f *(k ) P(t) = Φ0 (t − kT ) −Φ0 (t −(k +1)T ), |
|||||||||||||||
|
где Ф0(t) – функция Лепласа. Тогда: |
kδ |
k +1δ |
|||||||||||||
|
при k = 0: |
t −T |
||||||||||||||
|
P(t) = 0.5 + Φ |
0 |
( |
); |
||||||||||||
|
при k = 1: |
δ |
||||||||||||||
|
t −T |
t − 2T |
||||||||||||||
|
f |
* P(t) = Φ |
0 |
( |
) −Φ |
0 |
( |
); |
||||||||
|
при k = 2: |
δ |
2δ |
|||||||||||||
|
t − 2T |
t −3T |
||||||||||||||
|
f *2 * P(t) = Φ0 ( |
) −Φ0 ( |
). |
|||||||||||||
|
2δ |
3δ |
Функция Лапласа просто вычисляется в Excel. Оформим рабочий лист, как показано в табл. 2.9. В колонку А запишем значения t от 0 до 1800 часов с шагом 100 часов. Значения Т
δи поместим в ячейки G1 и H1 соответственно.
Вячейки В2 : Е2 запишем формулы, соответствующие вычислению функций P(t), f*P(t), f*(2)*Р(t) и Pc(t):

51
Из (2.20) получим вероятность безотказной работы с элементами, имеющими экспоненциальное время до отказа:
Pc, э (t) = (1+ 2λt) + 2(λt)2 e−2λt ,
где λ = T1 . В ячейку F2 поместим соответствующую формулу:
F2 = (1 + 2*А2/$М$1 + 2*(А2/$М$1)^2) * EXP(-2*A2/$M$1).
В результате копирования формул на ячейки ВЗ:F20 получим табл. 2.9.
Таблица 2.9
Расчеты вероятности безотказной работы для нормального и экспоненциального распределений
|
А |
В |
С |
D |
Е |
F |
|
|
1 |
t |
P(t) |
f*P(t) |
f(2)*P(t) |
Pc,n (t) |
Pc,n (t) |
|
2 |
0 |
1 |
2.87104Е-07 |
8J4349E-13 |
1,0000 |
1,0000 |
|
3 |
100 |
0,999968 |
3,16859Е-05 |
8J4349E-13 |
1,0000 |
0,9921 |
|
4 |
200 |
0.99865 |
0,001349959 |
8J4238E-13 |
1,0000 |
0,9526 |
|
5 |
300 |
0,97725 |
0,02274969 |
8,13349Е-13 |
1,0000 |
0,8795 |
|
6 |
400 |
0,841345 |
0,158644207 |
8.07798Е-13 |
1,0000 |
0,7834 |
|
7 |
500 |
0,5 |
0,499796482 |
7,93920Е-13 |
0,9996 |
0,6767 |
|
8 |
600 |
0,158655 |
0,839005810 |
7,80154Е-13 |
0,9953 |
0,5697 |
|
9 |
700 |
0,02275 |
0,960302572 |
7,74825Е-13 |
0,9664 |
0,4695 |
|
10 |
800 |
0,00135 |
0,920000380 |
7,73936Е-13 |
0,8489 |
0,3799 |
|
11 |
900 |
3,17Е-05 |
0,760218327 |
7J3936E-13 |
0,5780 |
0,3027 |
|
12 |
1000 |
2,87Е-07 |
0,499999713 |
7.73936Е-13 |
0,2500 |
0,2381 |
|
13 |
1100 |
9,9Е-10 |
0,239749986 |
7J3936E-13 |
0,0575 |
0,1851 |
|
14 |
1200 |
1Д9Е-12 |
0,078649653 |
7,73936Е-13 |
0,0062 |
0,1425 |
|
15 |
1300 |
0 |
0,016947366 |
7.73936Е-13 |
0,0003 |
0,1088 |
|
16 |
1400 |
0 |
0,002338930 |
7J3936E-13 |
0,0000 |
0,0824 |
|
17 |
1500 |
0 |
0,000203518 |
7,73936Е-13 |
0,0000 |
0,0620 |
|
18 |
1600 |
0 |
1.10526Е-05 |
7.73936Е-13 |
0,0000 |
0,0463 |
|
19 |
1700 |
0 |
3,72109Е-07 |
7J3936E-13 |
0,0000 |
0,0344 |
|
20 |
1800 |
0 |
7,73015Е-09 |
7,73936Е-13 |
0,0000 |
0,0255 |
Из таблицы видно, что функция f*(2)*P(t) практически не влияет на надежность всей системы. На основе колонок Е и F построены графики вероятностей безотказной работы Pc,н(t) и Pc,э(t) для нормального и экспоненциального случаев. Они представлены на рис. 2.14.
Графики вероятностей безотказной работы системы со скользящим резервом для рассмотренных законов распределения очень сильно отличаются друг от друга. В случае нормального распределения (с малой дисперсией) в течение отельного времени работы система практически абсолютно надежна, но в течение короткого времени она теряет ресурс и быстро становится ненадёжной.

52
Рис. 2.14. Вероятность безотказной работы системы при нормальном (кривая 1) и экспоненциальном (кривая 2) распределениях
2.3. Задачи для самостоятельного решения
2.1. Техническая система представляет собой дублированную систему с постоянно включенным резервом. Вероятность безотказной работы основной и резервной подсистем в течение t = 200 час равна 0,8. Найти вероятность безотказной работы и вероятность отказа системы в течение времени t. Найти среднее время безотказной работы системы при условии, что ее подсистемы имеют постоянную интенсивность отказа.
Ответ: Pc(t) = 0,96, Qс(t) = 0,04, T1c = 1344 час.
2.2. Интенсивность отказа элементов системы λ = 0,0025 час-1. Требуется определить кратность резервирования системы с постоянно включенным резервом, построенную из этих элементов, которая обеспечивает среднее время безотказной работы системы T1c = 800 час.
Ответ: m = 3 .
2.3. Найти показатели надежности резервированной системы с постоянным резервом кратности m = 3, элементы которой имеют интенсивности отказа λ 0 = 0,004 час-1, λ 1 = 0,007 час-1, λ 2 = 0,002 час-1, λ 3 = 0,001 час-1. Время непрерывной работы системы t = 120 час.
2.4.Определить показатели надежности мажоритарной системы, состоящей из 6 равнонадежных элементов, время до отказа которых равномерно распределено на интервале от 0 до 1000 часов. Количество резервных элементов равно 2. Получить аналитическое и графическое представления показателей надежности системы.
2.5.Получить формулу для вероятности безотказной работы мажоритарной системы, состоящей из элементов разной надежности при n = 4, m = 2.
2.6. Интенсивность отказа одного элемента λ = 0,0035 час-1. Требуется определить кратность резервирования системы (резерв замещением), построенную из этих элементов, которая обеспечивает среднее время безотказной работы системы Т1с = 800 час.
Ответ: m = 2.
2.7. Найти показатели надежности Pc(t), Tс, λ c(t) резервированной системы (резерв замещением) кратности m = 3, элементы которой имеют интенсивности отказа λ 0 = 0,04 час-1, λ 1 = 0,07 час-1, λ 2 = 0,02 час-1 , λ 3 = 0,1 час-1. Решение получить в виде формул, таблиц и графиков.
53
2.8.Для резерва замещением кратности m получить формулу вероятности безотказной работы, если элементы системы равнонадежны и имеют гамма-распределение времени до отказа с параметрами α иβ .
2.9.Для резерва замещением кратности m получить формулу плотности распределения времени безотказной работы при условии, что элементы системы равнонадежны и имеют нормальное распределение с параметрами m и β (δ < m / 3) .
2.10.Даны две системы со скользящим резервом. Первая система состоит из n = 7 элементов, из которых m = 3 резервных. Вторая система состоит из n = 5 элементов с m = 2 ре-
зервными. Определить более надежную систему по критерию вероятности безотказной работы. Элементы обеих систем имеют постоянную интенсивность отказа λ = 0,01 час-1.
2.11.Дана последовательно-параллельная система размером 3х5 (5 элементов нерезервированной системы, 3 резервных подсистемы) с постоянно включенным резервом. Все элементы имеют одинаковую надежность, время до отказа элементов имеет распределение Рэлея с математическим ожиданием Т = 50 час. Требуется определить вероятность безотказной работы системы при общем и раздельном резервировании. Провести сравнение по критерию
Рс(t).
Указание: воспользоваться формулами (2.8) и (2.14).
2.12.Дана последовательно-параллельная система размером 3×5 (5 элементов нерезер-
вированной системы, 3 резервных подсистемы), резервированная методом замещения. Все элементы имеют одинаковую интенсивность отказа λ = 0,02 час-1. Требуется определить вероятность безотказной работы системы при общем и раздельном резервировании. Провести
сравнение по критерию Pc(t).
Указание: воспользоваться формулами (2.9) и (2.15).
2.13.Элементы резервированной системы с постоянно включенным резервом имеют распределение Вейбулла времени работы до отказа. Найти выражение для среднего времени безотказной работы системы при кратности резервирования m = 0, 1, 2, 3, 4, 5 . Вычислить среднее время безотказной работы при параметрах закона распределения α = 2,5, β = 20.
Решение представить в виде таблицы.
2.14. Элементы резервированной системы с постоянно включенным резервом имеют усеченно-нормальное распределение времени до отказа. Найти выражение для среднего времени безотказной работы системы при кратности резервирования m = 0, 1, 2, 3, 4, 5. Вычислить значение среднего времени безотказной работы при параметрах закона распределения m0 = 380, δ 0 = 200. Решение представить в виде таблицы.
Указание: воспользоваться программными средствами символьной математики, напри-
мер Derive 5.
2.15. Даны две системы с постоянно включенным резервом с дробной кратностью резервирования m = 1/2 и m = 2/3 соответственно. Определить показатели надежности систем Pc(t), Tc, λ с(t). Решение представить в виде формул, графиков и таблиц. Известны следующие исходные данные для числового анализа: время работы системы t = 0…500 час, среднее время безотказной работы нерезервированной системы T = 550 час, основная и все резервные системы равнонадежны и имеют экспоненциальное распределение времени до отказа. Определить, какая из систем имеет более высокие показатели надежности.
2.16. Даны две системы, описанные в задаче 2.15. Определить критическое время tкр, свыше которого резервирование с дробной кратностью не целесообразно. Определить значение вероятности P(tкр). Решение получить в аналитическом и численном виде.
2.17. Даны две системы, описанные в задаче 2.15. Определить аналитические выражения интенсивностей отказов резервированных систем и найти предел lim λ c(t). Представить функцию λ c(t) в виде графика и объяснить полученный результат.
54
Ответ: 2 λ и 3 λ .
2.18. Резервированная система с постоянно включенным резервом состоит из двух подсистем, имеющих различные законы распределения времени до отказа. Необходимо вычислить Рс(t), Т1с, λ с(t). Решение получить в аналитическом виде, в виде графиков и таблиц. Графики представить в диапазоне t = 0..500 час. Исходные данные содержатся в табл. 2.10.
|
Законы распределения времени до отказа |
Таблица 2.10 |
|||||
|
Вариант |
Закон |
Вариант |
Закон |
Вариант |
Закон |
|
|
распределения |
распределения |
распределения |
||||
|
1 |
Ехр(0,005) |
6 |
W(1,2; 200) |
11 |
Ехр(0,0015) |
|
|
R(0,0002) |
TN(400; 180) |
TN(350; 180) |
||||
|
2 |
Ехр(0,004) |
7 |
N(360; 110) |
12 |
R(0,0001) |
|
|
N(400; 120) |
Г(4;95) |
TN(390; 190) |
||||
|
3 |
Ехр(0,007) |
8 |
N(410; 130) |
13 |
W(2; 100) |
|
|
Г(4; 120) |
R(0,0006) |
N(360; 100) |
||||
|
4 |
W(3; 50) |
9 |
R(0,0004) |
14 |
N(420; 140) |
|
|
R(0,0005) |
Г(3,2; 220) |
TN(380; 200) |
||||
|
5 |
W(l,5; 150) |
10 |
Ехр(0,001) |
15 |
TN(400;215) |
|
|
Г(2,5; 145) |
W(l,l; 160) |
Exp(0,002) |
||||
Указание: решение целесообразно получить с помощью систем символьной Математики, например Derive 5.
Практика
1. Расчет показателей безотказности
1.1 Вероятность безотказной работы
1.2 Вероятность отказа
1.3 Частота отказа
1.4 Интенсивность отказа
1.5 Средняя наработка до отказа
1.6 Среднее значение параметра потока отказов
1.7 Пример расчета показателей безотказности
2. Примеры расчета показателей надежности для различных законов распределения случайных величин
2.1 Экспоненциальный закон распределения
2.2 Закон распределения Вейбулла-Гнеденко
2.3 Закон распределения Рэлея
3. Примеры расчета показателей надежности сложных систем
3.1 Основное соединение элементов
3.2 Резервное соединение
1.1 Вероятность безотказной работы
Вероятностью безотказной работы называется вероятность того, что при определенных условиях эксплуатации, в пределах заданной наработки не произойдет ни одного отказа.
Вероятность безотказной работы обозначается как P(l), которая определяется по формуле (1.1):
где N0 – число элементов в начале испытания; r(l) – число отказов элементов к моменту наработки.Следует отметить, что чем больше величина N0, тем с большей точностью можно рассчитать вероятность P(l).
В начале эксплуатации исправного локомотива P(0) = 1, так как при пробеге l = 0 вероятность того, что ни один элемент не откажет, принимает максимальное значение – 1. С ростом пробега l вероятность P(l) будет уменьшаться. В процессе приближения срока эксплуатации к бесконечно большой величине вероятность безотказной работы будет стремиться к нулю P(l→∞) = 0. Таким образом в процессе наработки величина вероятности безотказной работы изменяется в пределах от 1 до 0. Характер изменения вероятности безотказной работы в функции пробега показан на рис. 1.1.
Рис.2.1. График изменения вероятности безотказной работы P(l)в зависимости от наработки
Основными достоинствами использования данного показателя при расчетах является два фактора: во-первых, вероятность безотказной работы охватывает все факторы, влияющие на надежность элементов, позволяя достаточно просто судить о его надежности, т.к. чем больше величина P(l), тем выше надежность; во-вторых, вероятность безотказной работы может быть использована в расчетах надежности сложных систем, состоящих из более чем одного элемента.
1.2 Вероятность отказа
Вероятностью отказа называют вероятность того, что при определенных условиях эксплуатации, в пределах заданной наработки произойдет хотя бы один отказ.
Вероятность отказа обозначается как Q(l), которая определяется по формуле (1.2):
В начале эксплуатации исправного локомотива Q(0) = 0, так как при пробеге l = 0 вероятность того, что хотя бы один элемент откажет, принимает минимальное значение – 0. С ростом пробега l вероятность отказа Q(l) будет увеличиваться. В процессе приближения срока эксплуатации к бесконечно большой величине вероятность отказа будет стремиться к единице Q(l→∞) = 1. Таким образом в процессе наработки величина вероятности отказа изменяется в пределах от 0 до 1. Характер изменения вероятности отказа в функции пробега показан на рис. 1.2.Вероятность безотказной работы и вероятность отказа являются событиями противоположными и несовместимыми.
Рис.2.2. График изменения вероятности отказа Q(l) в зависимости от наработки
1.3 Частота отказов
Частота отказов – это отношение числа элементов в единицу времени или пробега отнесенного к первоначальному числу испытуемых элементов. Другими словами частота отказов является показателем, характеризующим скорость изменения вероятности отказов и вероятности безотказной работы по мере роста длительности работы.
Частота отказов обозначается как 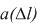
где – 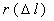
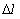
Данный показатель позволяет судить по его величине о числе элементов, которые откажут на каком-то промежутке времени или пробега, также по его величине можно рассчитать количество требуемых запасных частей.
Характер изменения частоты отказов в функции пробега показан на рис. 1.3.
Рис. 1.3. График изменения частоты отказов в зависимости от наработки
1.4 Интенсивность отказов
Интенсивность отказов представляет собой условную плотность возникновения отказа объекта, определяемую для рассматриваемого момента времени или наработки при условии, что до этого момента отказ не возник. Иначе интенсивность отказов – это отношение числа отказавших элементов в единицу времени или пробега к числу исправно работающих элементов в данный отрезок времени.
Интенсивность отказов обозначается как 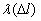
где
Как правило, интенсивность отказов 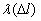
На рис. 1.4. представлен теоретический характер изменения интенсивности отказов в функции пробега.
Рис. 1.4. График изменения интенсивности отказов в зависимости от наработки
На графике изменения интенсивности отказов, изображенном на рис. 1.4. можно выделить три основных этапа отражающих процесс экс-плуатации элемента или объекта в целом.
Первый этап, который также называется этапом приработки, характеризуется увеличением интенсивности отказов в начальный период эксплуатации. Причиной роста интенсивности отказов на данном этапе являются скрытые дефекты производственного характера.
Второй этап, или период нормальной работы, характеризуется стремлением интенсивности отказов к постоянному значению. В течение этого периода могут возникать случайные отказы, в связи с появлением внезапной концентрации нагрузки, превышающей предел прочности элемента.
Третий этап, так называемый период форсированного старения. Характеризуется возникновением износовых отказов. Дальнейшая эксплуатация элемента без его замены становится экономически не рациональной.
1.5 Средняя наработка до отказа
Средняя наработка до отказа – это средний пробег безотказной работы элемента до отказа.
Средняя наработка до отказа обозначается как L1 и определяется по формуле (1.5):
где li – наработка до отказа элемента; ri – число отказов.
Средняя наработка до отказа может быть использована для предварительного определения сроков ремонта или замены элемента.
1.6 Среднее значение параметра потока отказов
Среднее значение параметра потока отказов характеризует среднюю плотность вероятности возникновения отказа объекта, определяемая для рассматриваемого момента времени.
Среднее значение параметра потока отказов обозначается как Wср и определяется по формуле (1.6):
1.7 Пример расчета показателей безотказности
Исходные данные.
В течение пробега от 0 до 600 тыс. км., в локомотивном депо произведен сбор информации по отказам ТЭД. При этом количество исправных ТЭД в начале периода эксплуатации составляло N0 = 180 шт. Суммарное количество отказавших ТЭД за анализируемый период составило ∑r(600000) = 60. Интервал пробега принять равным 100 тыс. км. При этом количество отказавших ТЭД по каждому участку составило: 2, 12, 16, 10, 14, 6.
Требуется.
Необходимо рассчитать показатели безотказности и построить их зависимости изменения во времени.
Сначала необходимо заполнить таблицу исходных данных так, как это показано в табл. 1.1.
Таблица 1.1.
Исходные данные к расчету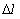 , тыс. км , тыс. км |
0 — 100 | 100 — 200 | 200 — 300 | 300 — 400 | 400 — 500 | 500 — 600 |
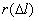 |
2 | 12 | 16 | 10 | 14 | 6 |
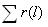 |
2 | 14 | 30 | 40 | 54 | 60 |
Первоначально по уравнению (1.1) определим для каждого участка пробега величину вероятности безотказной работы. Так, для участка от 0 до 100 и от 100 до 200 тыс. км. пробега вероятность безотказной работы составит:
Далее, используя зависимость (1.2) произведем расчет вероятности отказа ТЭД.
Произведем расчет частоты отказов по уравнению (1.3).
Далее по уравнению (1.4) произведем расчет интенсивности отказов ТЭД в зависимости от наработки.
Первоначально рассчитаем среднее количество работоспособных ТЭД на участке от 0 до 100 тыс. км. пробега:
Тогда интенсивность отказов на участке 0-100 тыс.км. будет равна:
Аналогичным образом определим величину интенсивности отказов для интервала 100-200 тыс. км.
По уравнениям (1.5 и 1.6) определим среднюю наработку до отказа и среднее значение параметра потока отказов.
Систематизируем полученные результаты расчета и представим их в виде таблицы (табл. 1.2.).
Таблица 1.2.
Результаты расчета показателей безотказности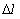 , тыс.км. , тыс.км. |
0 — 100 | 100 — 200 | 200 — 300 | 300 — 400 | 400 — 500 | 500 — 600 |
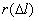 |
2 | 12 | 16 | 10 | 14 | 6 |
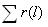 |
2 | 14 | 30 | 40 | 54 | 60 |
| P(l) | 0,989 | 0,922 | 0,833 | 0,778 | 0,7 | 0,667 |
| Q(l) | 0,011 | 0,078 | 0,167 | 0,222 | 0,3 | 0,333 |
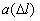 10-7, 1/км 10-7, 1/км |
1,111 | 6,667 | 8,889 | 5,556 | 7,778 | 3,333 |
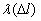 10-7, 1/км 10-7, 1/км |
1,117 | 6,977 | 10,127 | 6,897 | 10,526 | 4,878 |
Приведем характер изменения вероятности безотказной работы ТЭД в зависимости от пробега (рис. 1.5.). Необходимо отметить, что первой точкой на графике, т.е. при пробеге равном 0, величина вероятности безотказной работы примет максимальное значение – 1.
Рис. 1.5. График изменения вероятности безотказной работы в зависимости от наработки
Приведем характер изменения вероятности отказа ТЭД в зависимости от пробега (рис. 1.6.). Необходимо отметить, что первой точкой на графике, т.е. при пробеге равном 0, величина вероятности отказа примет минимальное значение – 0.
Рис. 1.6. График изменения вероятности отказа в зависимости от наработки
Приведем характер изменения частоты отказов ТЭД в зависимости от пробега (рис. 1.7.).
Рис. 1.7. График изменения частоты отказов в зависимости от наработки
На рис. 1.8. представлена зависимость изменения интенсивности отказов от наработки.
Рис. 1.8. График изменения интенсивности отказов в зависимости от наработки
2.1 Экспоненциальный закон распределения случайных величин
Экспоненциальный закон достаточно точно описывает надежность узлов при внезапных отказах, имеющих случайный характер. Попытки применить его для других типов и случаев отказов, особенно постепенных, вызванных износом и изменением физико-химических свойств элементов показали его недостаточную приемлемость.
Исходные данные.
В результате испытания десяти топливных насосов высокого давления получены наработки их до отказа: 400, 440, 500, 600, 670, 700, 800, 1200, 1600, 1800 ч. Предполагая, что наработка до отказа топливных насосов подчиняется экспоненциальному закону распределения.
Требуется.
Оценить величину интенсивности отказов , а также рассчитать вероятность безотказной работы за первые 500 ч. и вероятность отказа в промежутке времени между 800 и 900 ч. работы дизеля.
Во-первых, определим величину средней наработки топливных насосов до отказа по уравнению:
Затем рассчитываем величину интенсивности отказов:
Величина вероятности безотказной работы топливных насосов при наработке 500 ч составит:
Вероятность отказа в промежутке между 800 и 900 ч. работы насосов составит:
2.2 Закон распределения Вэйбулла-Гнеденко
Закон распределения Вейбулла-Гнеденко получил широкое распространение и используется применительно к системам, состоящим из рядов элементов, соединенных последовательно с точки зрения обеспечения безотказности системы. Например, системы, обслуживающие дизель-генераторную установку: смазки, охлаждения, питания топливом, воздухом и т.д.
Исходные данные.
Время простоя тепловозов в неплановых ремонтах по вине вспомогательного оборудования подчиняется закону распределения Вейбулла-Гнеденко с параметрами b=2 и a=46.
Требуется.
Необходимо определить вероятность выхода тепловозов из неплановых ремонтов после 24 ч. простоя и время простоя, в течение которого работоспособность будет восстановлена с вероятностью 0,95.
Найдем вероятность восстановления работоспособности локомотива после простоя его в депо в течение суток по уравнению:
Для определения времени восстановления работоспособности локомотива с заданной величиной доверительной вероятности также используем выражение:
2.3 Закон распределения Рэлея
Закон распределения Рэлея используется в основном для анализа работы элементов, имеющих ярко выраженный эффект старения (элементы электрооборудования, различного рода уплотнения, шайбы, прокладки, изготовленные из резиновых или синтетических материалов).
Исходные данные.
Известно, что наработки контакторов до отказа по параметрам старения изоляции катушек можно описать функцией распределения Рэлея с параметром S = 260 тыс.км.
Требуется.
Для величины наработки 120 тыс.км. необходимо определить вероятность безотказной работы, интенсивность отказов и среднюю наработку до первого отказа катушки электромагнитного контактора.
3.1 Основное соединение элементов
Система, состоящая из нескольких независимых элементов, связанных функционально таким образом, что отказ любого из них вызывает отказ системы, отображается расчетной структурной схемой безотказной работы с последовательно соединенными событиями безотказной работы элементов.
Исходные данные.
Нерезервированная система состоит из 5 элементов. Интенсивности их отказов соответственно равны 0,00007; 0,00005; 0,00004; 0,00006; 0,00004 ч-1
Требуется.
Необходимо определить показатели надежности системы: интенсивность отказов, среднее время наработки до отказа, вероятность безотказной работы, частота отказов. Показатели надежности P(l) и a(l) получить в интервале от 0 до 1000 часов с шагом в 100 часов.
Вычислим интенсивность отказа и среднюю наработку до отказа по следующим уравнениям:
Значения вероятности безотказной работы и частоты отказов получим, используя уравнения приведенные к виду:
Результаты расчета P(l) и a(l) на интервале от 0 до 1000 часов работы представим в виде табл. 3.1.
Таблица 3.1.
Результаты расчета вероятности безотказной работы и частоты отказов системы на интервале времени от 0 до 1000 ч.| l, час | P(l) | a(l), час-1 |
| 0 | 1 | 0,00026 |
| 100 | 0,974355 | 0,000253 |
| 200 | 0,949329 | 0,000247 |
| 300 | 0,924964 | 0,00024 |
| 400 | 0,901225 | 0,000234 |
| 500 | 0,878095 | 0,000228 |
| 600 | 0,855559 | 0,000222 |
| 700 | 0,833601 | 0,000217 |
| 800 | 0,812207 | 0,000211 |
| 900 | 0,791362 | 0,000206 |
| 1000 | 0,771052 | 0,0002 |
Графическая иллюстрация P(l) и a(l) на участке до средней наработки до отказа представлена на рис. 3.1, 3.2.
Рис. 3.1. Вероятность безотказной работы системы.
Рис. 3.2. Частота отказов системы.
3.2 Резервное соединение элементов
Исходные данные.
На рис. 3.3 и 3.4 показаны две структурные схемы соединения элементов: общего (рис. 3.3) и поэлементного резервирования (рис. 3.4). Вероятности безотказной работы элементов соответственно равны P1(l) = P ’1(l) = 0,95; P2(l) = P’2(l) = 0,9; P3(l) = P ’3(l) = 0,85.
Требуется.
Необходимо рассчитать надежность двух систем.
Рис. 3.3. Схема системы с общим резервированием.
Рис. 3.4. Схема системы с поэлементным резервированием.
Вероятность безотказной работы блока из трех элементов без резервирования рассчитаем по выражению:
Вероятность безотказной работы той же системы при общем резервировании (рис. 3.3) составит:
Вероятности безотказной работы каждого из трех блоков при поэлементном резервировании (рис. 3.4) будут равны:
Вероятность безотказной работы системы при поэлементном резервировании составит:
Таким образом, поэлементное резервирование дает более существенное увеличение надежности (вероятность безотказной работы возросла с 0,925 до 0,965, т.е. на 4%).
Исходные данные.
На рис. 3.5 представлена система с комбинированным соединением элементов. При этом вероятности безотказной работы элементов имеют следующие значения: P1=0,8; Р2=0,9; Р3=0,95; Р4=0,97.
Требуется.
Необходимо определить надежность системы. Также необходимо определить надежность этой же системы при условии, что резервные элементы отсутствуют.
Рис.3.5. Схема системы при комбинированном функционировании элементов.
Для расчета в исходной системе необходимо выделить основные блоки. В представленной системе их три (рис. 3.6). Далее рассчитаем надежность каждого блока в отдельности, а затем найдем надежность всей системы.
Рис. 3.6. Сблокированная схема.
Надежность системы без резервирования составит:
Таким образом, система без резервирования является на 28% менее надежной, чем система с резервированием.
Надежность автоматизированной системы является комплексной характеристикой системы и состоит из нескольких показателей, основными из которых являются безотказность и ремонтопригодность. Безотказность численно характеризуется средней наработкой до отказа (MTTF — «Mean Time to Failure»), обозначается буквой , или интенсивностью отказов
(«Average probability of failure per hour»), а также вероятностью безотказной работы
в течение заданного времени
.
Ремонтопригодность характеризуется средним временем восстановления после отказа (MTTR — «Mean Time To Repair») или вероятностью восстановления в течение заданного времени.
Для расчета показателей надежности сложных систем, состоящих из большого количества элементов, используют метод декомпозиции (расчет надежности по частям). Если показатели надежности отдельных элементов (в том числе резервированных) заданы или рассчитаны, то вероятность безотказной работы системы рассчитывают следующим образом. Событие, состоящее в безотказной работе -того элемента системы, обозначают символами
, а противоположное событие (отказ элемента) обозначают как
. Отказ системы без резервирования наступает при отказе хотя бы одного элемента. Поэтому событие, состоящее в безотказной работе системы
, равно произведению событий
, т. е.
, где
— количество элементов в системе. Вероятность произведения независимых событий равна произведению вероятностей событий. Поэтому вероятность работоспособного состояния системы равна
|
(8.9) |
Учитывая зависимость вероятности безотказной работы элементов от времени (8.5) для каждого -того элемента, предыдущее выражение можно записать в виде
где
|
(8. 11) |
— интенсивность отказа всей системы;
— интенсивность отказа
-того элемента.
Поскольку в эксплуатационной документации обычно указывают среднюю наработку до отказа, которая связана с интенсивностью отказов соотношением (8.8), то, пользуясь выражением (8.11), наработку до отказа всей системы можно представить в виде
|
|
(8.12) |
где — наработка до отказа
-того элемента.
В частности, для системы из одинаковых элементов с наработкой
=
|
(8.13) |
т. е. наработка на отказ системы обратно пропорциональна количеству ее элементов.
Резервированный элемент (контроллер, датчик и др.) при расчете надежности можно рассматривать как один элемент системы, если для него найдены показатели надежности.
Поскольку в системах автоматизации используются, как правило, только два вида резервирования: горячее резервирование замещением и резервирование методом голосования, то при расчете их показателей безотказности можно обойтись без аппарата цепей Маркова [Александровская], ограничившись алгеброй случайных событий и теорией вероятностей. При расчете вероятности отказа «теплое» резервирование не отличается от горячего.
В случае горячего резервирования два элемента (например, два ПЛК) находятся постоянно во включенном состоянии и при отказе одного из них в работу включается второй. Если считать, что общие элементы, обеспечивающие процесс резервирования, абсолютно надежны, то безотказная работа резервированной системы , состоящей из двух ПЛК, будет обеспечена, если работоспособен хотя бы один из них. Обозначим событие, состоящее в безотказной работе 1-го элемента как
, 2-го как
, а противоположные им события (отказы элементов) как
и
. Тогда событие, состоящее в работоспособности резервированной системы (в данном примере система состоит из двух ПЛК), будет иметь место, если работоспособен первый ПЛК и одновременно работоспособен второй (
) ИЛИ работоспособен первый и отказал второй (
) ИЛИ отказал первый и работоспособен второй: (
), т.е.
Найдем теперь вероятность работоспособности системы , пользуясь тем, что события
,
и
несовместны (т.е. не могут иметь место в одно и то же время), следовательно, вероятность суммы событий равна сумме вероятностей каждого из них, а вероятность произведения событий равна произведению вероятностей:
Здесь использовано также свойство .
Поскольку элементы в резервированной системе идентичны, то и, обозначая
, получим
|
(8.16) |
Подставляя сюда вместо его зависимость от времени (8.5), получим вероятность безотказной работы системы при горячем резервировании в виде
|
(8.17) |
где — интенсивность отказов элемента без резервирования.
Плотность распределения времени до отказа (частота отказов) согласно (8.6) равна
|
(8.18) |
а среднее время наработки до отказа
|
(8.19) |
где — средняя наработка на отказ одного контроллера. Интеграл в (8.19) берется по частям.
Рассуждая аналогично, можно получить вероятность безотказной работы системы из трех элементов, например, трех контроллеров, в схеме голосования 2оо3. Обозначим события, состоящие в работоспособности трех элементов соответственно и
, а противоположные им события (отказы) — как
и
. Тогда резервированная система будет работоспособной, если работоспособны первый И второй И отказал третий контроллер ИЛИ работоспособен первый И третий И отказал второй контроллер ИЛИ работоспособен второй И третий И отказал первый контроллер ИЛИ работоспособны все три контроллера одновременно, т.е.
|
(8. 20) |
Переходя от событий к их вероятностям и учитывая, что слагаемые в (8.20) являются событиями несовместными, а также считая, что все контроллеры идентичны, т.е. , получим:
поэтому
|
(8. 22) |
Графики зависимостей (8.17) и (8.22) показаны на (рис. 8.21-а).
Плотность распределения времени до отказа (частота отказов) согласно (8.6) равна
|
(8.23) |
а среднее время наработки до отказа
|
(8.24) |
где — средняя наработка на отказ одного контроллера.
Обратим внимание, что средняя наработка до отказа у системы с голосованием получилась ниже, чем у нерезервированной системы. Это объясняется тем, что система с тремя контроллерами и голосованием по схеме 2оо3 не является троированной, а имеет дробную кратность резервирования 1:2, т.е. в ней резервный элемент — один, а резервируемых — два, поскольку в схеме голосования только наличие двух работоспособных контроллеров обеспечивает работоспособность системы. Поэтому эффект снижения безотказности вследствие нарастания числа элементов в системе (8.13) при больших наработках оказывается сильнее эффекта резервирования. График вероятности безотказной работы для системы с голосованием (рис. 8.21-б) идет ниже, чем у системы без резервирования, начиная с некоторого значения наработки, а средняя наработка до отказа получается меньше.
|
|
|
|
а) |
б) |
|
Рис. 8.21. Вероятность безотказной работы ПЛК с |
Сравнение систем только по средней наработке до отказа может вводить в заблуждение так же, как «средняя температура по больнице». Такое сравнение эффективно только для случаев, когда функциональные зависимости элементов имеют одинаковый вид. Для систем с резервированием это условие не выполняется. Поэтому следует делать сравнение по более информативному показателю — вероятности безотказной работы, которая у системы с голосованием в течение практически всего времени эксплуатации значительно больше, чем у системы без резервирования (рис. 8.21-а и -б).
Графики, приведенные на рис. 8.21, иллюстрируют вероятность безотказной работы системы, в которой после отказа одного из элементов не выполняется его замена или ремонт. Если же замена элемента производится сразу, то понятие вероятности безотказной работы теряет значение, поскольку после замены вероятность отказа без замены элемента реализоваться не может. Актуальной становится длительность перехода на резерв, а также продолжительность выполнения горячей замены или восстановления после отказа. Поэтому для обслуживаемых систем автоматизации целью резервирования является обеспечение непрерывности процесса управления или увеличение коэффициента готовности, но не увеличение вероятности безотказной работы. По этим же характеристикам система с голосованием превосходит все остальные.
Проделанный выше сравнительный анализ двух методов резервирования не может быть использован для систем безопасности, в которых вероятности опасного и безопасного отказов различны. Если в системах 2оо3, где требуется безотказность, после отказа двух элементов наступает отказ всей системы, то в системах безопасности опасный отказ наступает только после того, как исчерпаны все варианты деградации (например, 2оо3 — 1оо2 — 1001 — 0). Таким образом, для анализа вероятности опасного отказа система 2оо3 имеет кратность резерва не 2:1, а 1:2, т.е. она является троированной; после отказа одного элемента становится дублированной, после отказа двух элементов становится не резервированной и только после отказа всех трех элементов наступает отказ системы. Кроме того, для анализа систем, связанных с безопасностью, важна не вероятность отказа, а вероятность отказа при наличии запроса [МЭК] которая рассчитывается иным путем.
Поскольку автоматизированная система выполняет множество самостоятельных задач (функций), то параметры надежности по ГОСТ 24.701-86 [ГОСТ] оцениваются не для всей системы, а для каждой выполняемой функции отдельно.
При количественных оценках параметров надежности, а также при интерпретации полученных результатов следует учитывать достоверность исходных данных. Существующие методы экспериментальной оценки показателей надежности [ГОСТ, ГОСТ] были разработаны во времена, когда наработка на отказ вычислительных машин (EC-1061, «Электроника Д3-28» и др.) составляла от нескольких часов до нескольких суток. Экспериментальный материал по отказам, собранный в течение месяца, был достаточен не только для оценки наработки на отказ, но даже для построения функций распределения, изучения зависимостей параметров надежности от условий эксплуатации (температуры, вибрации, влажности и т. п.).
С тех пор ситуация изменилась коренным образом. Появилась технология поверхностного монтажа, увеличилась степень интеграции микросхем, были разработаны новые материалы для монтажа и изготовления печатных плат. Надежность электронных изделий возросла настолько, что экспериментальные данные невозможно накопить в достаточном количестве не только при стендовых испытаниях у изготовителя, но даже путем анализа отказов изделий, возвращенных потребителями в течение гарантийного срока (такая методика используется фирмой GE Fanuc [Programmable]). Так, из 30 тыс. модулей ввода-вывода RealLab! серии NL [Денисенко], проданных фирмой RealLab!, в течение гарантийного срока не было ни одного возврата по причине аппаратного отказа.
Кроме того, ПЛК не относятся к изделиям массового производства и поэтому за период между сменой их поколений количество отказавших изделий может оказаться недостаточным для расчета наработки на отказ. Получить же зависимость показателей надежности от условий эксплуатации еще более проблематично.
Ускоренные испытания [Федоров], широко применяемые в полупроводниковом производстве, неприменимы к ПЛК из-за невозможности экспериментального или расчетного определения коэффициентов подобия.
В то же время органы сертификации, в соответствии с существующими стандартами, требуют обязательного указания параметров надежности в ТУ и эксплуатационной документации на изделие. Одним из реально осуществимых методов оценки показателей надежности является использование статистических данных объектов-аналогов по ГОСТ 27.301-95 [ГОСТ]. Поскольку аналоги, как правило, являются изделиями, изготовленными по устаревшей технологии, показатели надежности оказываются заниженными, по крайне мере, на порядок.
Рассмотрим, например, вероятность безотказной работы процессора CPU 313C-2DP фирмы Siemens, на который изготовителем указывается наработка на отказ (MTBF) =16,9 лет [Product]. В соответствии с (8.4) и (8.5), вероятность отказа процессора в течение гарантийного срока 18 мес. будет равна
=0,08. Поскольку оценка вероятности отказа рассчитывается как доля отказавших изделий в испытуемой партии, то, например, из 1000 находящихся в эксплуатации процессоров в течение гарантийного срока должны отказать в среднем 80 шт. и только 920 шт. остаться исправными. Однако любой пользователь продукции Siemens скажет, что эта цифра отличается от реальной, по крайней мере, на порядок. Можно было бы предположить, что наработка на отказ занижена потому, что при ее экспериментальном определении условия испытаний были выбраны предельными. Однако документ «Reliability Consulting» («Консультация по надежности»), расположенный рядом с таблицей наработок на отказ [Reliability] указывает только одно условие: температура при испытаниях составляет 40 °С, и не дает методики пересчета для других условий эксплуатации. Выглядит странным также указание наработки на отказ тремя значащими цифрами, что по теории погрешностей должно означать, что приведенные данные отличаются от действительных не более чем на 1%.
Наличие большого числа парадоксов наводит на мысль, что показатели надежности, указываемые производителями электронных средств автоматизации, определяются политическими, а не техническими факторами, и по мере совершенствования технологии производства мы будем наблюдать только снижение достоверности этих показателей. В этих условиях о надежности изделий лучше судить по общей репутации фирмы и наличии системы управления качеством на базе стандартов ISO 9001 или ISO 9014, но не по наработке на отказ.
Продолжая использовать наш сайт, вы даете согласие на обработку файлов cookies и персональных данных в соответсвии с политикой. Окей, не возражаю

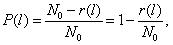
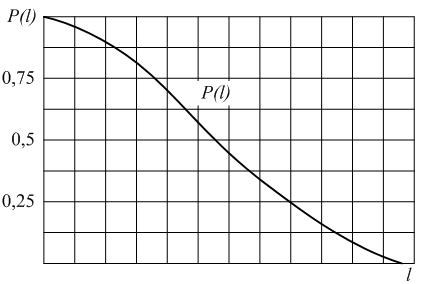
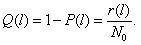
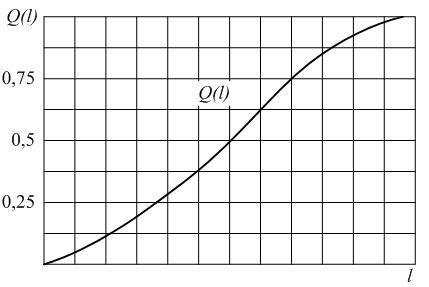
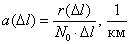
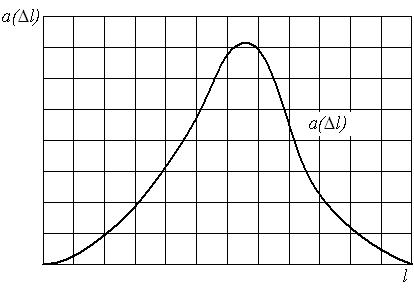
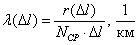
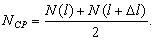
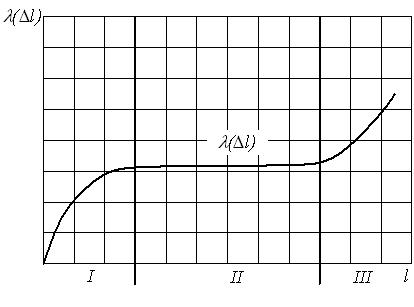
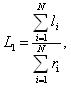
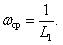
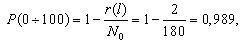
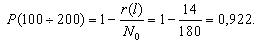
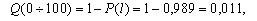
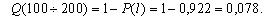
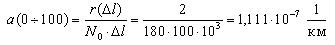
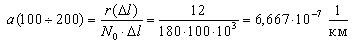
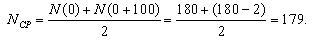
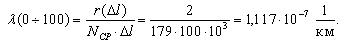
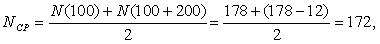
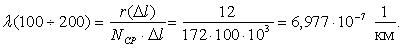
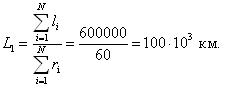
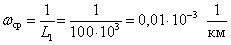
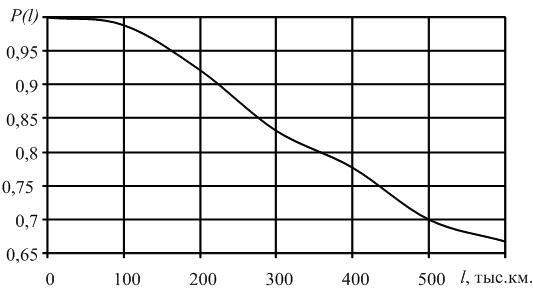
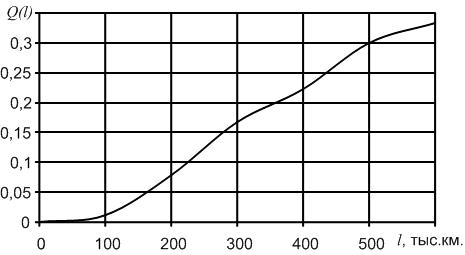
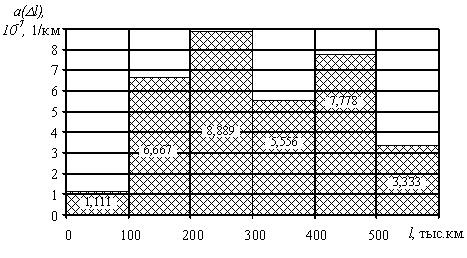
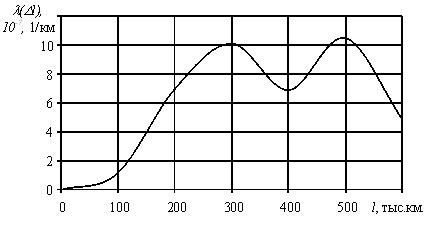
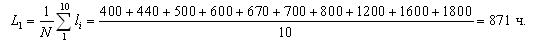
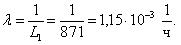
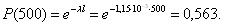
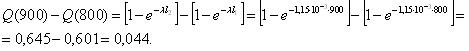
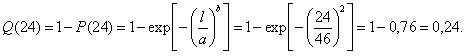
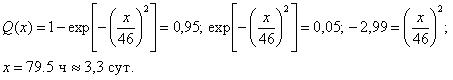
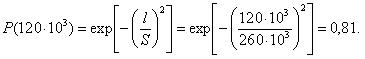
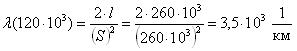
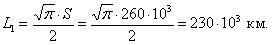
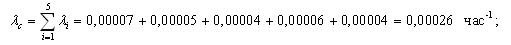
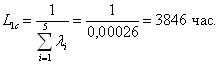
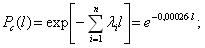
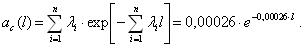
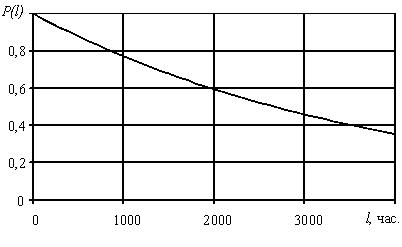
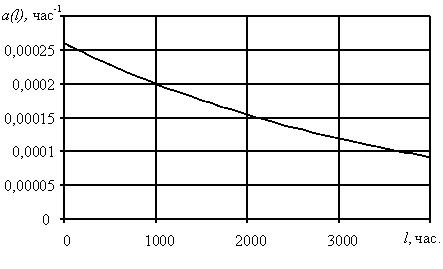
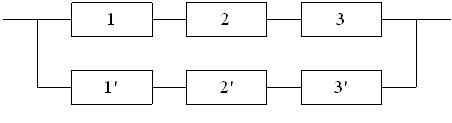
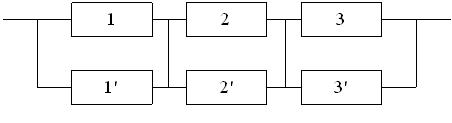
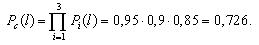
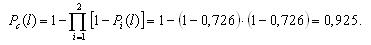
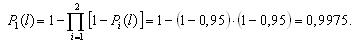
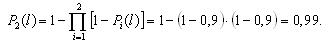
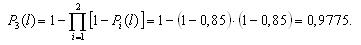
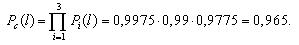
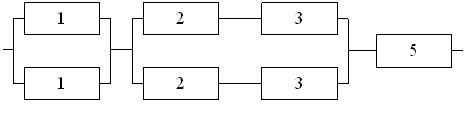
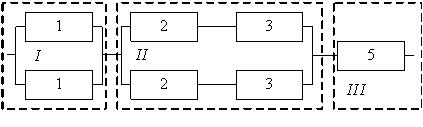
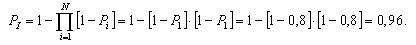
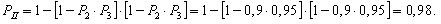
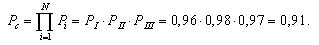
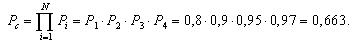
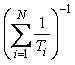 ,
,