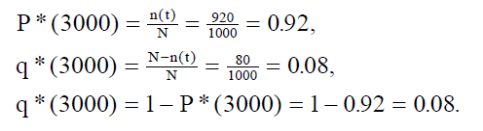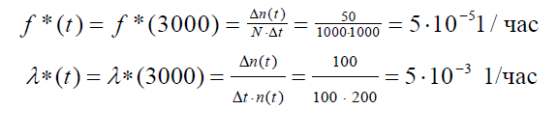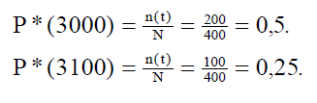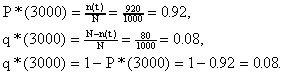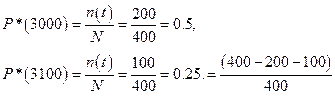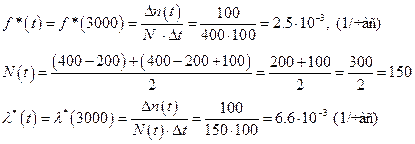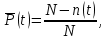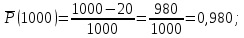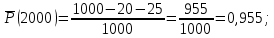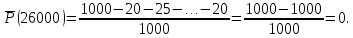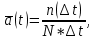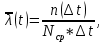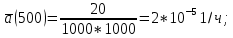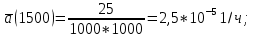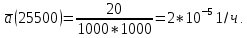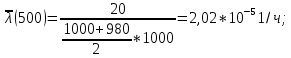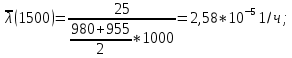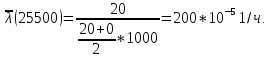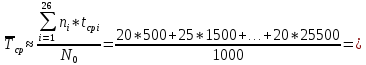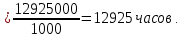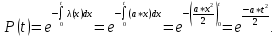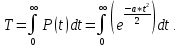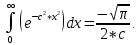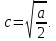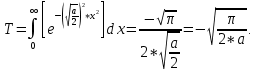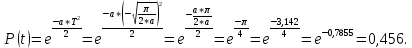Расчет показателей надежности технических систем
Методические
указания по выполнению практических
работ
по
дисциплине «Надежность систем»
221400.62
«Управление качеством»
профиль
«Управление качеством в
производственно-технологических
системах»
Курск
Практическая
работа №1
Определение
количественных характеристик надежности
по
статистическим данным об отказах изделия
Вероятность
безотказной работы
по статистическим данным об отказах
оценивается выражением
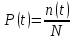
где
n(t)
число изделий, не отказавших к моменту
времени t;
Nчисло
изделий, поставленных на испытания;
Р(t)
статистическая оценка вероятности
безотказной работы изделия.
Для
вероятности
отказа
по статистическим данным справедливо
соотношение
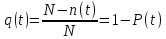
где
N—n(t)
число изделий, отказавших к моменту
времени t;
q(t)
— статистическая оценка вероятности
отказа изделия.
Частота
отказов
по статистическим данным об отказах
определяется выражением

где
Δn(t)
– число отказавших изделий на участке
времени (t,
t+Δt);
f(t)
– статистическая оценка частоты отказов
изделия; Δt
– интервал времени.
Интенсивность
отказов
по статистическим данным об отказах
определяется формулой
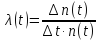
где
n(t)
– среднее число изделий, не отказавших
к моменту времени t;
Δn(t)
– число отказавших изделий на участке
времени (t,
t+Δt);
λ
(t)
– статистическая оценка интенсивности
отказов изделия.
Среднее
время безотказной работы
изделия по статистическим данным
оценивается выражением
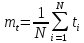
где
ti
– время безотказной работы i—
го изделия; N
– общее число изделий, поставленных на
испытания; mt
– статистическая оценка среднего
времени безотказной работы изделия.
Для
определения mt
по формуле (5) необходимо знать моменты
выхода из строя всех N
изделий.
Задача
1.
На испытание поставлено 1000 однотипных
электронных ламп, за 3000 час. отказало
80 ламп. Требуется определить P(t),
q(t)
при t
= 3000 час.
Решение.
В данном случае N=
1000; n(t)=1000-80=920;
N—n(t)=1000-920=80.
По формулам (1) и (2) определяем
Задача
2.
На испытание было поставлено 1000 однотипных
ламп. За первые 3000 час. отказало 80 ламп,
а за интервал времени 3000 — 4000 час. отказало
еще 50 ламп. Требуется определить
статистическую оценку частоты и
интенсивности отказов электронных ламп
в промежутке времени 3000 — 4000 час.
Решение.
В данном случае N=1000;
t=3000
час; Δt
=1000 час; Δn(t)=50;
n(t)=920.
По
формулам (3) и (4) находим
Задача
3.
На испытание поставлено N = 400 изделий.
За время t = 3000 час отказало 200 изделий,
т.е. n(t) = 400-200=200.За интервал времени (t,
t+Δt) , где Δt= 100 час, отказало 100 изделий,
т.е. Δn(t)= 100. Требуется определить Р*(3000),
P*(3100), f*(3000), λ*(3000).
Решение.
По формуле (1) находим
Используя
формулы (3) и (4), получим
Задача4.
На испытание поставлено 6 однотипных
изделий. Получены следующие значения
ti
(ti
время 6езотказной работы i—
го изделия) : t1
=280 час; t2
= 350 час; t3
=400 час; t4
=320 час; t5
=380 час; t6
=330 час.
Определить
статистическую оценку среднего времени
безотказной работы изделия.
Решение.
По формуле (5) имеем
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #


Подборка по базе: Тест с ответами Версия 13.1 от 17.11.2021. Временные методически, Тест с ответами по теме Методические рекомендации COVID-19 Верс, Тема 6. Г. Компьютерные технологии подготовки текстовых документ, Проектирование современного урока на основе системно-деятельност, Метод указания по курсовой работе ОП 05 ДО.pdf, Теоретические и методические основы физического воспитания и раз, Кейс на основе анализа собственного жизненного опыта.docx, Методические указания и темы контрольных работ.docx, _ 2 курс Методические рекомендации по подготовке и защите курсов, Экономическая безопасность. Методические указания по написанию к
- Предисловие
- Назначение методических указаний
Методические указания составлены на основе «Требований к разработке методических указаний для студентов по проведению лабораторных работ и практических занятий» и предназначены для обучающихся по специальности СПО 220703 Автоматизация технологических процессов и производств.
Выбор содержания и объем конкретного практического занятия обусловлен сложностью учебного материала для усвоения, междисциплинарными связями и учетом значения конкретного практического занятия для приобретения обучающимися соответствующих умений и компетенций, предусмотренных ФГОС.
- Требования к умениям и общим компетенциям
В результате выполнения заданий практических занятий обучающийся должен
уметь:
— рассчитывать надежность систем управления и отдельных модулей и
подсистем мехатронных устройств и систем;
— определять показатели надежности систем управления;
— осуществлять контроль соответствия устройств и функциональных блоков
мехатронных и автоматических устройств и систем управления;
— проводить различные виды инструктажей по охране труда;
Обучающийся должен овладеть профессиональными и общими компетенциями:
| Код | Наименование результата обучения |
| ПК 5.1. | Осуществлять контроль параметров качества систем автоматизации |
| ПК 5.2. | Проводить анализ характеристик надежности систем автоматизации |
| ПК 5.3. | Обеспечивать соответствие состояния средств и систем автоматизации требованиям надежности |
| ОК 2. | Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество |
| ОК 3. | Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность |
| ОК 4. | Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития |
| ОК 5. | Использовать информационно-коммуникационные технологии в профессиональной деятельности |
| ОК 6. | Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями |
| ОК 7. | Брать на себя ответственность за работу членов команды (подчиненных), результат выполнения заданий |
| ОК 8. | Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации |
| ОК 9. | Ориентироваться в условиях частой смены технологий в профессиональной деятельности |
| ОК 10. | Исполнять воинскую обязанность, в том числе с применением полученных профессиональных знаний (для юношей) |
2. Правила выполнения практических заданий
1. Прежде, чем приступить к выполнению заданий практического занятия, обучающийся должен подготовить ответы на теоретические вопросы к практическому занятию.
2. Перед началом каждой работы проверяется готовность обучающегося к практическому занятию.
3. После выполнения заданий практического занятия обучающийся должен представить отчет о проделанной работе в рабочей тетради и подготовиться к обсуждению полученных результатов и выводов.
4. Обучающийся, пропустивший практическое занятие по уважительной или неуважительной причинам, обязан выполнить работу в дополнительно назначенное время.
5. Оценка за работу обучающемуся выставляется с учетом предварительной подготовки к работе, доли самостоятельности при ее выполнении, точности и грамотности оформления отчета по работе:
— оценка «5» (отлично) ставится: задания практического занятия выполнены в полном объеме, в соответствии с заданием, с соблюдением последовательности выполнения, расчеты выполнены без ошибок, самостоятельно; работа оформлена аккуратно;
— оценка «4» (хорошо) ставится: задания практического занятия выполнены в полном объеме, в соответствии с заданием, с соблюдением последовательности выполнения, частично с помощью преподавателя, присутствуют незначительные ошибки в расчетах; работа оформлена аккуратно;
— оценка «3» (удовлетворительно) ставится: задания практического занятия выполнены в полном объеме, в соответствии с заданием, частично с помощью преподавателя, присутствуют ошибки при замерах и расчетах; по оформлению работы имеются замечания;
— оценка «2» (неудовлетворительно)ставится: обучающийся не подготовился к практическому занятию, при расчетах допустил грубые ошибки, по оформлению работы имеются множественные замечания.
Практическая работа №1
Тема: Определение вероятности безотказной работы.
Цель:
- рассмотреть основные показатели безотказной работы (вероятность безотказной работы и вероятность отказа).
Основные понятия:
- Показатели надежности
- Вероятность безотказной работы
- Вероятность отказа
Теоретические сведения
Работоспособность – это состояние изделия, при котором оно способно выполнять заданную функцию с параметрами, установленными требованиями технической документации, в течение расчётного срока службы.
Отказ – это нарушение работоспособности. Свойство элемента или системы непрерывно сохранять работоспособность при определённых условиях эксплуатации (до первого отказа) называется безотказностью.
Безотказность – свойство объекта сохранять работоспособное состояние в течение некоторого времени или наработки.
- Показатели надежности.
Показатели надежности – количественная характеристика одного или нескольких свойств, составляющих надежность объекта.
Для оценки, расчетов и исследования надежности технических устройств в процессе их проектирования и эксплуатации используются количественные характеристики (критерии надежности). Для показателей надежности используются две формы представления:
- Статистическая – при эксперементальном исследовании надежности технических систем
- Вероятностная – при априорных аналитических расчетах надежности.
В соответствии с ГОСТ 27.002 – 89 показатели надежности подразделяются на:
Классификация показателей надежности
Число характерезуемых свойств надежности
Единичный показатель надежности – показатель, характеризующий одно из свойств, составляющих надежность объекта. (Например, вероятность отказа, средний срок службы и т.п.).
Комплексный показатель надежности – показатель, характеризующий одновременно несколько свойств, составляющих надежность объекта. (Например, коэффициент готовности, удельная суммарная трудоемкость ремонтов и т.п.).
Свойство надежности
Безотказность
Долговечность
Сохраняемость
Ремонтопригодность
Метод получения
Расчетный показатель надежности – показатель, значения которого определяют расчетным методом.
Экспериментальный показатель надежности – показатель, точечную или интервальную оценку которого определяют по данным испытания.
Эксплуатационный показатель надежности – показатель, точечную или интервальную оценку которого определяют по данным эксплуатации.
Экстраполированный показатель надежности – показатель, точечную или интервальную оценку которого определяют на основании результатов расчетов, испытаний и (или) эксплуатационных данных путем экстраполирования на другую продолжительность эксплуатации и другие условия эксплуатации.
Область использования
Нормативный показатель, регламентированный в НТД
Оценочный показатель, используемый для различных сравнительных оценок при научно-исследовательских и проектно-технологических разработках
Область распространения
Групповой показатель надежности – служит для оценки надежности совокупности изделий данного типа.
Индивидуальный показатель надежности – предназначен для оценки надежности каждого изделия данного типа.
Вероятность безотказной работы по статистическим данным об отказах оценивается выражением
| (1.1) |
где N(t) — число изделий, не отказавших к моменту времени t; N0— число изделий, поставленных на испытания; Р(t) — статистическая оценка вероятности безотказной работы изделия.
Для вероятности отказа по статистическим данным справедливо соотношение
| (1.2) |
где n(t)- число изделий, отказавших к моменту времени t; Q(t) — статистическая оценка вероятности отказа изделия.
Частота отказов по статистическим данным об отказах определяется выражением
| (1.3) |
где Δn(Δt) — число отказавших изделий на участке времени (t, t+Δt); f(Δt) — статистическая оценка частоты отказов изделия; Δt — интервал времени.
Интенсивность отказов по статистическим данным об отказах определяется формулой
| (1.4) |
где n(Δt)- число отказавших изделий на участке времени (t-Δt/2-, t+Δt/2) ; N(t) – среднее число изделий, продолжающих исправно работать на участке времени (t, t+Δt), определяется по формуле 1.5; λ(t)- статистическая оценка интенсивности отказов изделия.
| (1.5) |
Где -количество исправных объектов через время ; — количество исправных объектов через время
Среднее время безотказной работы изделия по статистическим данным оценивается выражением
| (1.6) |
где ti— время безотказной работы i- го изделия; N— общее число изделий, поставленных на испытания; Тср — статистическая оценка среднего времени безотказной работы изделия.
Пример решения типовых задач
Задача 1.1. На испытание поставлено 1000 однотипных электронных ламп, за 3000 час. отказало 80 ламп. Требуется определить P*(t), q*(t) при t = 3000 час.Решeниe. В данном случае = 1000; N(t)=1000-80=920; n(t)= 80. По формулам (1.1) и (1. 2) определяем
Задача 1.2. На испытание было поставлено 1000 однотипных ламп. За первые 3000 час. отказало 80 ламп, а за интервал времени 3000 — 4000 час. отказало еще 50 ламп. Требуется определить статистическую оценку частоты и интенсивности отказов электронных ламп в промежутке времени 3000 — 4000 час.Решение. В данном случае N=1000; t=3000 час; =1000 час; n(t)=80; (t)=50.
По формулам (1.3) и (1.4) находим
час ;
;
Задача 1.3. На испытание поставлено = 400 изделий. За время t = 3000 час отказало 200 изделий, т.е. n(t) = 400-200=200.За интервал времени (t, t+ ) , где = 100 час, отказало 100 изделий, т.е. n(t)= 100. Требуется определить Р*(3000),
P*(3100), f*(3000), *(3000).
Решение. По формуле (1.1) находим
Используя формулы (1.3) и (1.4), получим
Задача1.4. На испытание поставлено 6 однотипных изделий. Получены следующие значения ti (ti — время безотказной работы i- го изделия) : t1 =280 час; t2 = 350 час; t3 =400 час; t4 =320 час; t5 =380 час; t6 =330 час.
Определить статистическую оценку среднего времени безотказной работы изделия.
Решение. По формуле (1.5) имеем час.
Варианты задач для самостоятельного решения
Задача 1. На испытание поставлено изделий. За время t час вышло из строя n(t) штук изделий. За последующий интервал времени вышло из строя изделий. Необходимо вычислить вероятность безотказной работы за время t и , частоту отказов
и интенсивность отказов
на интервале . Исходные данные для решения задачи приведены в таблице 1.
Таблица 1
Исходные данные для задачи 1
Задания для самостоятельной работы
Задача 1.1. На испытание поставлено 200 однотипных изделий. За 2000 ч отказало 50 изделий. За последующие 100 часов отказало ещё 5 изделий. Требуется определить:
1. статистическую оценку вероятности безотказной работы за время работы t1 = 2000 час и t2 = 2100 час;
2. статистическую оценку вероятности отказа за время работы t1 = 2000 час и t2 = 2100 час;
3. оценку плотности распределения отказов и интенсивности отказов в промежутке времени между t1 = 2000 час и t2 = 2100 час.
Задача 1.2. На испытание поставлено 100 однотипных изделий. За 4000 часов работы отказало 50 изделий. Определить статистические оценки вероятности безотказной работы и вероятности отказа за время работы 4000 часов.
Задача 1.3. На испытание поставлено 100 однотипных изделий. За 4000 часов работы отказало 50 изделий. За последующие 50 часов еще 5 изделий. Дать оценку плотности распределения отказов и интенсивности отказов в промежутке времени между t1 = 4000 час и t2 = 4050 час.
Задача 1.4. В течение 500 часов работы из 20 буровых насосов отказало 2. За интервал времени 500 – 520 часов отказал еще один буровой насос. Дать оценку плотности распределения отказов и интенсивности отказов в промежутке времени между t1 = 500 час и t2 = 520 час.
Задача 1.5. На испытание поставлено 2000 подшипников качения. За первые 3000 часов отказало 80 изделий. За интервал времени 3000 – 4000 часов отказало еще 50 подшипников. Требуется определить статистическую оценку вероятности безотказной работы за время 4000 часов.
Задача 1.6. В течение 500 часов работы из 20 буровых насосов отказало 2. За интервал времени 500 – 520 часов отказал еще один буровой насос. Требуется определить статистическую оценку вероятности отказа за время 520 часов.
Задача 1.7. На испытание поставлено 600 изделий. За время 1200 часов вышло из строя 125 штук изделий. За последующий интервал времени 1200 – 1250 часов вышло из строя еще 13 изделий. Необходимо определить статистическую оценку вероятности безотказной работы и вероятности отказа за время работы t1 = 1200 час и t2 = 1250 час; оценку плотности распределения отказов и интенсивности отказов в промежутке времени между t1 = 1200 час и t2 = 1250 час.
Задача 1.8. На испытание поставлено 10 однотипных изделий. Получены следующие значения времени безотказной работы: t1 = 580 час; t2 = 720 час; t3 = 860 час; t4 = 550 час; t5 = 780 час; t6 = 830 час; t7 = 910 час; t8 = 850 час; t9 = 840 час; t10 = 750 час. Определить статистическую оценку среднего времени безотказной работы изделия.
Контрольные вопросы:
1. Что такое безотказность?
2. Какие показатели надежности являются показателями безотказности?
3. Что такое вероятность безотказной работы?
4. Что такое вероятность отказа?
5. Как определяются статистические оценки вероятности безотказной работы и вероятности отказа?
6. Как определяется плотность распределения наработки?
7. Что такое интенсивность отказов?
8. Кривая зависимости интенсивности отказа во времени.
9. Дайте определение средней наработки до отказа и средней наработки до первого отказа.
Литература:
1. Острейковский В.А. Теория надежности: учебник для вузов. – 2-е изд., испр. – М.: Высшая школа, 2008. – 464 с.;
Практическая работа №2-4
Тема: Определение частоты отказов. Определение интенсивности отказов. Определение среднего времени безотказной работы.
Цель:
- рассмотреть основные показатели частоты отказов, интенсивности отказов, среднего времени безотказной работы.
Основные понятия:
- Частота отказов
- Интенсивность отказов
- Среднее время безотказной работы
Задача 1.
Допустим, что на испытании находилось 1000 однотипных изделий. Число отказавших ламп учитывалось через каждые 1000 часов работы. Данные об отказах ламп сведены в таблицу. Требуется определить вероятность безотказной работы, частоту отказов и интенсивность отказов в функции времени, построить графики этих функций. Необходимо также найти среднюю наработку до первого отказа.
| ti, час | n(ti) | ti, час | n(ti) | ti, час | n(ti) |
| 0–1 000 | 20 | 9 000–10 000 | 30 | 18 000–19 000 | 50 |
| 1 000–2 000 | 25 | 10 000–11 000 | 40 | 19 000–20 000 | 35 |
| 2 000–3 000 | 35 | 11 000–12 000 | 40 | 20 000–21 000 | 35 |
| 3 000–4 000 | 50 | 12 000–13 000 | 50 | 21 000–22 0C0 | 50 |
| 4 000–5 000 | 30 | 13 000–14 000 | 40 | 22 000–23 000 | 35 |
| 5 000–6 000 | 50 | 14 000–15 000 | 50 | 23 000–24 000 | 25 |
| 6 000–7 000 | 40 | 15 000–16 0С0 | 40 | 24 000–25 000 | 30 |
| 7 000–8 000 | 40 | 16 000–17 000 | 50 | 25 000–26 000 | 20 |
| 8 000–9 000 | 50 | 17 000–18 000 | 40 | – | – |
Решение:
Вероятность безотказной работы по статистическим данным об отказах оценивается выражением:
где 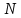
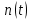
Получаем:
………………………..
Значения 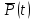
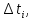
Таблица 1
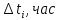 |
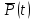 |
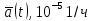 |
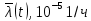 |
| 0-1000 | 0,980 | 2 | 2,02 |
| 1000-2000 | 0,955 | 2,5 | 2,58 |
| 2000-3000 | 0,920 | 3,5 | 3,73 |
| 3000-4000 | 0,870 | 5 | 5,59 |
| 4000-5000 | 0,840 | 3 | 3,51 |
| 5000-6000 | 0,790 | 5 | 6,13 |
| 6000-7000 | 0,750 | 4 | 5,19 |
| 7000-8000 | 0,710 | 4 | 5,48 |
| 8000-9000 | 0,660 | 5 | 7,30 |
| 9000-10000 | 0,630 | 3 | 4,65 |
| 10000-11000 | 0,590 | 4 | 6,56 |
| 11000-12000 | 0,550 | 4 | 7,02 |
| 12000-13000 | 0,500 | 5 | 9,52 |
| 13000-14000 | 0,460 | 4 | 8,33 |
| 14000-15000 | 0,410 | 5 | 11,49 |
| 15000-16000 | 0,370 | 4 | 10,26 |
| 16000-17000 | 0,320 | 5 | 14,49 |
| 17000-18000 | 0,280 | 4 | 13,33 |
| 18000-19000 | 0,230 | 5 | 19,61 |
| 19000-20000 | 0,195 | 3,5 | 16,47 |
| 20000-21000 | 0,160 | 3,5 | 19,72 |
| 21000-22000 | 0,110 | 5 | 37,04 |
| 22000-23000 | 0,075 | 3,5 | 37,84 |
| 23000-24000 | 0,050 | 2,5 | 40,00 |
| 24000-25000 | 0,020 | 3 | 85,71 |
| 25000-26000 | 0 | 2 | 200,00 |
Частоту отказов определяем по следующему выражению:
где 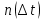
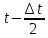
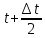
Интенсивность отказов определяем по следующему выражению:
где 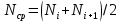
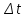
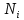
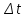
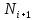
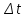
Получаем:
………………………..
………………………..
Отметим, что данные по частотам и интенсивностям отказов рассчитывались на основании середин интервалов. Значения 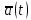
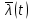
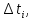
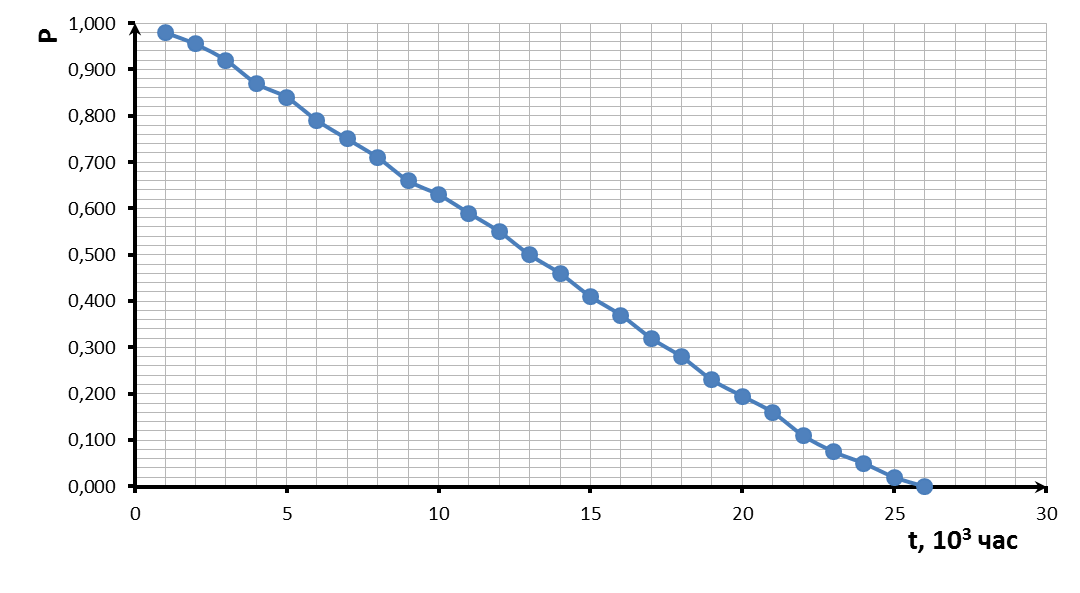
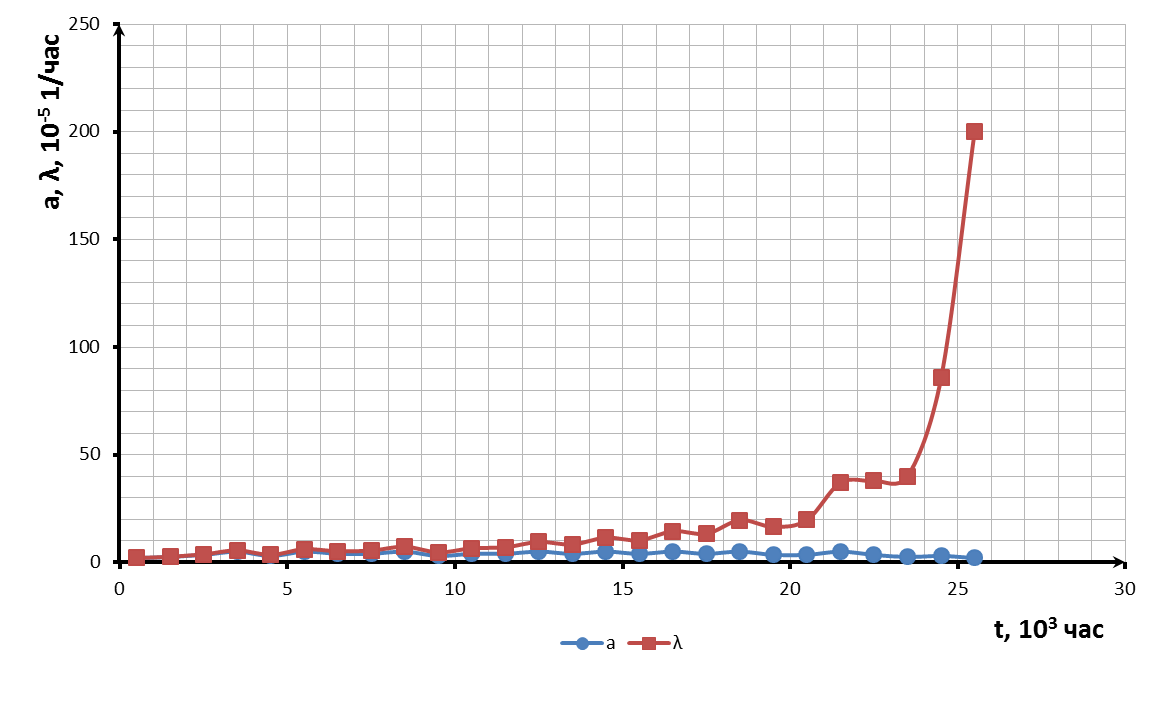
На рисунках 1 и 2 строим требуемые графические зависимости.
Рисунок 1. Вероятность безотказной работы
Рисунок 2. Частота и интенсивность отказов
Вычислим среднее время безотказной работы:
Задача 2.
Какова вероятность безотказной работы объекта в течение средней наработки до отказа, если аналитическое выражение интенсивности отказов имеет вид 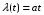
Решение:
По заданному выражению для интенсивности отказов определяем выражение для вероятности безотказной работы:
Для определения средней наработки на отказ воспользуемся следующим соотношением:
Известно, что:
Применительно к нашей задаче:
Таким образом, получаем:
Следовательно, вероятность безотказной работы исследуемой автоматизированной системы в течение средней наработки до отказа будет равна:
ЗАДАНИЕ. На основе представленных статистических данных провести расчет и анализ показателей надежности серии невосстанавливаемых объектов.
Пример выполнения задания
Исходные данные: Число изделий, поставленных на испытание, N = 1000 изделий. Испытания проводятся в течение 100 часов. Каждые сто часов определялось количество отказов изделий. Результаты испытаний представлены в таблице 2.1.
Средним временем безотказной работы называется математическое ожидание времени безотказной работы.
Эта характеристика надежности обозначается T. Как всякое математическое ожидание случайной величины среднее время безотказной работы определяется из выражения:
. (1.25)
Приведенное определение является вероятностным. Для определения среднего времени безотказной работы из статистических данных пользуются формулой:
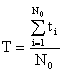
где ti— время безотказной работы i-го образца, N0— число образцов, над которыми проводится испытание.
Из выражения (1.26) видно, что для определения T необходимо знать моменты отказов всех образцов аппаратуры, над которыми проводится эксперимент. При большом числе образцов N0 это может сильно усложнить эксперимент.
Выражение (1.26) является статистическим определением среднего времени безотказной работы.
Среднее время безотказной работы является одной из наиболее наглядных количественных характеристик надежности. Однако этой характеристике надежности свойственны существенные недостатки. Как математическое ожидание случайной величины, она не может полностью характеризовать время работы аппаратуры. Необходимо еще знать, по меньшей мере, дисперсию времени отказов аппаратуры. Кроме того, T фактически не позволяет оценить надежность аппаратуры, время работы которой во много раз меньше среднего времени безотказной работы.
Из выражения (1.26) видно, что для вычисления T определяются времена отказов каждого из N0 образцов. В дальнейшем они в эксперименте не участвуют. Таким образом, среднее время безотказной работы характеризует надежность аппаратуры до первого отказа. Это означает, что T хорошо характеризует надежность аппаратуры разового использования, например, простейших элементов, которые после отказа не ремонтируются.
Величину T можно использовать и для оценки надежности сложных устройств. Однако в этом случае T характеризует надежность до первого их отказа.
У аппаратуры длительного использования, работающей в режиме смены отказавших элементов, среднее время безотказной работы до первого отказа может существенно отличаться от среднего времени между первым и вторым отказами, вторым и третьим и т.д. Это означает, что среднее время безотказной работы может характеризовать надежность такой аппаратуры только до первого отказа.
Поэтому надежность аппаратуры длительного использования оценивают, в отличие от среднего времени безотказной работы, так называемой наработкой на отказ.
Этой характеристике дают следующее определение: наработкой на отказ называется среднее значение времени между соседними отказами, при условии восстановления каждого отказавшего элемента.
Эта характеристика обозначается tср и определяется из статистических данных об отказах по формуле:
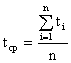
где ti – время исправной работы аппаратуры между (i – 1)-м и i-м отказами; n – число отказов аппаратуры за время t.
Из определения и формулы (1.27) видно, что наработка на отказ является средним временем между соседними отказами. Формулой (1.27) удобно пользоваться, если tср определяется по данным об отказах лишь одного образца аппаратуры. Если испытание проводится с несколькими образцами, то tср вычисляется по формуле:
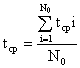
где tср.i — среднее время между соседними отказами i-го образца, вычисленное по формуле (1.27), N0 – число испытываемых образцов.
Найти связь среднего времени между соседними отказами с другими количественными характеристиками надежности проще всего через среднюю частоту отказов. Действительно, если известны средние частоты отказов элементов сложной системы, то среднее число отказов системы в любом промежутке времени определяется ее суммарной частотой отказов. Тогда среднее время между соседними отказами будет равно величие, обратной суммарной частоте отказов, т.е.
(1.29)
или
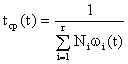
где r – число типов элементов.
Вероятность безотказной работы P(t), частота отказов α(t) (средняя частота отказов ), интенсивность отказов
и среднее время безотказной работы T (среднее время между соседними отказами tср) являются основными количественными характеристиками надежности. Каждая из них имеет свои достоинства и недостатки. Ни одна из них не является исчерпывающей характеристикой надежности. Только все они в совокупности во многих случаях могут характеризовать достаточно полно надежность аппаратуры в течение времени ее работы.