Компания выбирает место для строительства торгово‐развлекательного комплекса: на месте квартала старых одноэтажных домов в центре города или на окраине города. Стоимость прокладки 1 метра коммуникаций равна 6000 рублей. В аренду планируется сдавать 4000 м2 площади комплекса. Стоимость земли, цена строительства комплекса с учётом сноса старых зданий и предполагаемая стоимость сдачи даны в таблице.
| Место | Цена земли (млн руб.) |
Цена строительства (млн руб.) |
Длина коммуникаций (м) |
Стоимость аренды за 1 м2 (руб./месяц) |
|---|---|---|---|---|
| Центр | 64,4 | 176 | 200 | 1200 |
| Окраина | 11,2 | 168 | 3500 | 900 |
Обдумав оба варианта, компания выбрала местом для строительства центр города. Через сколько месяцев после начала сдачи в аренду торговых площадей построенного комплекса более высокая стоимость аренды компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций? Ответ округлите до целых.
На плане (см. рис.) изображён район города, в котором живёт Петя. Сторона каждой клетки на плане равна 10 м.
Дом, в котором живёт Петя, обозначен цифрой 6. Прямо напротив дома, где живёт Петя, через дорогу находится дом в форме буквы «Г», где живёт его друг Вася. Рядом с домом, где живёт Петя, расположен дом, где живёт одноклассница Таня, а напротив него через дорогу имеется здание банка площадью 600 м2. А с другой стороны дома, где живёт Таня, расположен детский сад. Недалеко от детского сада и дома, где живёт Петя, находится магазин. Также имеется автобусная остановка, обозначенная цифрой 4, а в десяти метрах от неё — квартал старых одноэтажных домов.
1
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Банк | Магазин | Дом, где живёт Таня |
Квартал старых домов |
|---|---|---|---|---|
| Цифры |
Источник: Тренировочный вариант № 231, усложнённая версия, Александр Ларин
2
Территорию стадиона необходимо засеять газонной травой. В одной упаковке газонной травы содержится 12 кг семян, при этом для засеивания 3 м2 земли необходимо 100 г семян. Какое минимальное количество упаковок газонной травы необходимо приобрести?
Источник: Тренировочный вариант № 231, усложнённая версия, Александр Ларин
3
Найдите суммарную площадь, которую занимают дома, где проживают Таня, Петя и Вася. Ответ дайте в м2.
Источник: Тренировочный вариант № 231, усложнённая версия, Александр Ларин
4
Найдите расстояние от дома, где живёт Петя, до автобусной остановки (расстояние между двумя ближайшими точками по прямой) в метрах.
Источник: Тренировочный вариант № 231, усложнённая версия, Александр Ларин
Спрятать решение
Решение.
Стоимость постройки ТРК в центре города равна
рублей.
Стоимость постройки ТРК на окраине города равна
рублей.
Разница в стоимости составляет
рублей.
Разница в стоимости аренды составляет
рублей.
Значит, более высокая стоимость аренды компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций через месяцев. Округляя, получаем ответ — 35 месяцев.
Ответ: 35.
Источник: Тренировочный вариант № 231, усложнённая версия, Александр Ларин
Фирма выбирает место для строительства гостиницы: в центре города или на его окраине. Стоимость прокладки 1 метра коммуникаций равна 5500 рублей. В гостинице планируется сдавать 500 номеров. Стоимость земли, цена строительства гостиницы и средняя стоимость номера даны в таблице.
| Место | Цена земли (млн руб.) |
Цена строительства (млн руб.) |
Длина коммуникаций (м) |
Стоимость номера (руб./сутки) |
|---|---|---|---|---|
| Центр | 58,2 | 136 | 200 | 3200 |
| Окраина | 11,3 | 128 | 2800 | 2800 |
Обдумав оба варианта, компания выбрала местом для строительства центр города. Через сколько суток после начала сдачи номеров (при условии полной загрузки гостиницы) более высокая стоимость номеров компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций?
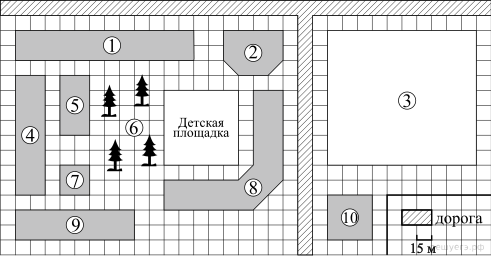
На плане (см. рисунок) изображён район города, в котором проживает Вика. Сторона каждой клетки на плане равна 15 м. Рядом с домом Вики, обозначенным на плане цифрой 4, находится одноэтажный магазин площадью 900 м2 и фитнес‐центр. В 15 м от магазина расположен дом, где живёт одноклассник Вики Артём. В 30 м от детской площадки находится дом, где живёт Олег. Если выйти из фитнес‐центра, пройти небольшой ельник, обозначенный цифрой 6, и детскую площадку, то приходишь к угловому дому, где живёт дедушка Вики. Рядом с ним находится мастерская по ремонту бытовой техники. Через дорогу от дома дедушки расположен рынок, а недалеко от него – мебельный центр площадью 2025 м2.
Решение.
Стоимость постройки гостиницы в центре города равна

Стоимость постройки гостиницы на окраине города равна

Разница в стоимости составляет

Разница в стоимости номера составляет

Значит, более высокая стоимость номеров компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций через 
Ответ: 203.
ОГЭ математика
126 вариант
1. Для объектов, указанных в таблице, определите, какими цифрами они
обозначены на схеме. Заполните таблицу, в ответ запишите последовательность
четырёх цифр.
|
Объекты |
Магазин |
Фитнес‐центр |
Мастерская |
Дом, где |
|
Цифры |
На плане (см. рисунок) изображён район города, в котором проживает
Вика. Сторона каждой клетки на плане равна 15 м. Рядом с домом Вики,
обозначенным на плане цифрой 4, находится одноэтажный магазин площадью
900 м2 и фитнес‐центр. В 15 м от магазина расположен
дом, где живёт одноклассник Вики Артём. В 30 м от детской площадки
находится дом, где живёт Олег. Если выйти из фитнес‐центра, пройти
небольшой ельник, обозначенный цифрой 6, и детскую площадку, то приходишь к
угловому дому, где живёт дедушка Вики. Рядом с ним находится мастерская по
ремонту бытовой техники. Через дорогу от дома дедушки расположен рынок, а
недалеко от него – мебельный центр площадью 2025 м2.
2. Детскую площадку решили покрыть резиновой плиткой размером
1 м × 1 м каждая. Плитка продаётся упаковками по 16 штук. Какое минимальное
количество упаковок плитки необходимо приобрести?
3. Найдите суммарную площадь, которую занимают магазин и
фитнес-центр. Ответ дайте в м2.
4. По периметру детской площадки планируется поставить забор. Найдите
его длину (в метрах).
5. Фирма выбирает место для строительства гостиницы: в центре города
или на его окраине. Стоимость прокладки 1 метра коммуникаций равна 5500 рублей.
В гостинице планируется сдавать 500 номеров. Стоимость земли, цена
строительства гостиницы и средняя стоимость номера даны в таблице.
|
Место |
Цена земли |
Цена |
Длина |
Стоимость |
|
Центр |
58,2 |
136 |
200 |
3200 |
|
Окраина |
11,3 |
128 |
2800 |
2800 |
Обдумав оба варианта, компания выбрала местом для строительства
центр города. Через сколько суток после начала сдачи номеров (при условии
полной загрузки гостиницы) более высокая стоимость номеров компенсирует
разность в стоимости земли, строительства и прокладывания коммуникаций?
6. Найдите значение выражения
7. На координатной прямой отмечены числа r, q и p.
Какая из разностей q − p, q − r, r − p положительна?
В
ответе укажите номер правильного варианта.
1) q − p
2) q − r
3) r − p
4) ни одна из них
8. Найдите значение выражения при
9. Решите уравнение .
10. Девятиклассники Петя, Катя, Ваня, Даша и Наташа бросили жребий,
кому начинать игру. Найдите вероятность того, что начинать игру должен будет
мальчик.
11. Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А)
Б)
B)
ГРАФИКИ
В таблице под каждой буквой укажите соответствующий номер.
12. Радиус описанной около треугольника окружности можно найти по
формуле , где
—
сторона треугольника, — противолежащий этой стороне
угол, а — радиус описанной около этого треугольника окружности. Пользуясь этой
формулой, найдите , если
, а
.
13. Укажите решение неравенства
1)
2)
3)
4)
14. При свободном падении тело прошло в первую секунду 5 м, а в каждую
следующую на 10 м больше. Найдите глубину шахты, если свободно падающее тело
достигло его дна через 5 с после начала падения.
15.
Найдите острый угол параллелограмма , если биссектриса
угла образует со стороной
угол, равный 41°. Ответ дайте в
градусах.
16. 
окружности равна 72, а расстояние от центра окружности до этой хорды равно 27.
Найдите диаметр окружности.
17. Сторона ромба равна 5, а диагональ равна 6. Найдите площадь ромба.
18.
На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный
треугольник. Найдите длину его большего катета.
19. Какие из следующих утверждений верны?
1. Через точку, не лежащую на данной прямой, можно провести
прямую, параллельную этой прямой.
2. В тупоугольном треугольнике все углы тупые.
3. Любой квадрат является прямоугольником.
В
ответ запишите номера выбранных утверждений без пробелов, запятых и других
дополнительных символов.
20. Найдите значение выражения если
21. Из городов А и В навстречу друг другу одновременно выехали
мотоциклист и велосипедист. Мотоциклист приехал в В на 42 минуты раньше, чем
велосипедист приехал в А, а встретились они через 28 минут после выезда.
Сколько часов затратил на путь из В в А велосипедист?
22. Найдите все значения , при которых неравенство
не имеет
решений.
23.
Найдите угол АСО, если его сторона СА касается
окружности, О — центр окружности, а дуга AD окружности,
заключённая внутри этого угла, равна 100°
24. В параллелограмме ABCD диагонали AC и BD пересекаются
в точке K. Докажите, что площадь параллелограмма ABCD в
четыре раза больше площади треугольника AKB.
25. На стороне BC остроугольного треугольника ABC (AB≠AC)
как на диаметре построена полуокружность, пересекающая высоту AD в
точке M, AD = 15, MD = 3, H —
точка пересечения высот треугольника ABC. Найдите AH.
Решение
1. Для объектов, указанных в таблице, определите, какими цифрами они
обозначены на схеме. Заполните таблицу, в ответ запишите последовательность
четырёх цифр.
|
Объекты |
Магазин |
Фитнес‐центр |
Мастерская |
Дом, где |
|
Цифры |
На плане (см. рисунок) изображён район города, в котором проживает
Вика. Сторона каждой клетки на плане равна 15 м. Рядом с домом Вики,
обозначенным на плане цифрой 4, находится одноэтажный магазин площадью
900 м2 и фитнес‐центр. В 15 м от магазина расположен
дом, где живёт одноклассник Вики Артём. В 30 м от детской площадки
находится дом, где живёт Олег. Если выйти из фитнес‐центра, пройти
небольшой ельник, обозначенный цифрой 6, и детскую площадку, то приходишь к
угловому дому, где живёт дедушка Вики. Рядом с ним находится мастерская по
ремонту бытовой техники. Через дорогу от дома дедушки расположен рынок, а
недалеко от него – мебельный центр площадью 2025 м2.
Решение.
Рядом с домом Вики, обозначенным на плане цифрой 4, находится
одноэтажный магазин площадью 900 м2 и фитнес‐центр. Значит,
магазин отмечен цифрой 7, а фитнес-центр — цифрой 5. 30 м от детской площадки
находится дом, где живёт Олег. Следовательно, дом, где живёт Олег, обозначен
цифрой 1. Если выйти из фитнес‐центра, пройти небольшой ельник, обозначенный цифрой 6, и детскую
площадку, то приходишь к угловому дому, где живёт дедушка Вики. Рядом с ним
находится мастерская по ремонту бытовой техники. Значит, мастерская отмечена
цифрой 2.
Ответ: 7521.
2. Детскую площадку решили покрыть резиновой плиткой размером
1 м × 1 м каждая. Плитка продаётся упаковками по 16 штук. Какое минимальное
количество упаковок плитки необходимо приобрести?
Решение.
Найдём площадь детской площадки:
м2.
Одна плитка имеет площадь 1 м2. Значит,
потребуется упаковок плитки.
Таким образом, необходимо приобрести 352 упаковки плитки.
Ответ: 352.
3. Найдите суммарную площадь, которую занимают магазин и
фитнес-центр. Ответ дайте в м2.
Решение.
Площадь, которую занимают магазин и фитнес-центр, равна
м2.
Ответ: 2700.
4. По периметру детской площадки планируется поставить забор. Найдите
его длину (в метрах).
Решение.
Найдём периметр детской площадки — это сумма длин четырех сторон,
по 5 клеток каждая:
м.
Ответ: 300.
5. Фирма выбирает место для строительства гостиницы: в центре города
или на его окраине. Стоимость прокладки 1 метра коммуникаций равна 5500 рублей.
В гостинице планируется сдавать 500 номеров. Стоимость земли, цена
строительства гостиницы и средняя стоимость номера даны в таблице.
|
Место |
Цена земли |
Цена |
Длина |
Стоимость |
|
Центр |
58,2 |
136 |
200 |
3200 |
|
Окраина |
11,3 |
128 |
2800 |
2800 |
Обдумав оба варианта, компания выбрала местом для строительства
центр города. Через сколько суток после начала сдачи номеров (при условии
полной загрузки гостиницы) более высокая стоимость номеров компенсирует
разность в стоимости земли, строительства и прокладывания коммуникаций?
Решение.
Стоимость постройки гостиницы в центре города равна
рублей.
Стоимость постройки гостиницы на окраине города равна
рублей.
Разница в стоимости составляет
рублей.
Разница в стоимости номера составляет
рублей.
Значит, более высокая стоимость номеров компенсирует разность в
стоимости земли, строительства и прокладывания коммуникаций через дня.
Ответ: 203.
6. Найдите значение выражения
Решение.
Вычислим:
Ответ: 5,25.
7. На координатной прямой отмечены числа r, q и p.
Какая из разностей q − p, q − r, r − p положительна?
В
ответе укажите номер правильного варианта.
1) q − p
2) q − r
3) r − p
4) ни одна из них
Решение.
Заметим, что r < q < p. Разность
положительна только в том случае, когда вычитаемое меньше уменьшаемого. Это
верно только для разности q − r.
Правильный ответ указан под номером: 2.
8. Найдите значение выражения при
Решение.
Упростим выражение
Подставим значения :
Ответ: -60
9. Решите уравнение .
Решение.
Умножим уравнение на 7, получим:
10. Девятиклассники Петя, Катя, Ваня, Даша и Наташа бросили жребий,
кому начинать игру. Найдите вероятность того, что начинать игру должен будет
мальчик.
Решение.
Из пятерых детей — мальчиков двое. Поэтому вероятность равна
Ответ: 0,4.
11. Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А)
Б)
B)
ГРАФИКИ
В таблице под каждой буквой укажите соответствующий номер.
Решение.
Определим вид графика каждой из функций:
А) —
уравнение параболы, ветви которой направлены вниз
Б) — уравнение
гиперболы
B) — уравнение
прямой
Найдём для каждого графика функцию: A — 3, Б — 2, В — 1.
Ответ: 321.
12. Радиус описанной около треугольника окружности можно найти по
формуле , где
—
сторона треугольника, — противолежащий этой стороне
угол, а — радиус описанной около этого треугольника окружности. Пользуясь этой
формулой, найдите , если
, а
.
Решение.
Выразим из формулы :
Подставляя, получаем:
Ответ: 0,4.
13. Укажите решение неравенства
1)
2)
3)
4)
Решение.
Последовательно получаем:
Правильный ответ указан под номером: 1.
Ответ: 1
14. При свободном падении тело прошло в первую секунду 5 м, а в каждую
следующую на 10 м больше. Найдите глубину шахты, если свободно падающее тело
достигло его дна через 5 с после начала падения.
Решение.
Составим математическую модель задачи: в первую секунду — 5 м, во
вторую секунду — 15 м, в третью секунду — 25 м, в четвертую секунду — 35 м, в
пятую секунду — 45 м.
Всего
за пять секунд — 5 + 15 + 25 + 35 + 45 = 125 (м).
Ответ: глубина шахты 125 м.
Приведем
другое решение.
Пути, пройденные телом за каждую секунду, представляют собой
арифметическую прогрессию с первым членом a1 = 5 и
разностью d = 10. Путь, пройденный телом за 5 секунд, найдем по
формуле суммы арифметической прогрессии при n = 5:
15.
Найдите острый угол параллелограмма , если биссектриса
угла образует со стороной
угол, равный 41°. Ответ дайте в
градусах.
Решение.

обозначения, как показано на рисунке. Углы и
равны
как накрест лежащие углы при параллельных прямых и
Поскольку
—
биссектриса угла
Сумма смежных углов
параллелограмма равна поэтому угол
равен
Таким образом, острый угол параллелограмма равен
Ответ: 82.
16. 
окружности равна 72, а расстояние от центра окружности до этой хорды равно 27.
Найдите диаметр окружности.
Решение.

построение и введём обозначения, как показано на рисунке. Рассмотрим
треугольники и
они
прямоугольные, — общая,
и
равны
как радиусы окружности, следовательно, эти треугольники равны, откуда По
теореме Пифагора найдём радиус окружности:
Диаметр равен двум радиусам, следовательно,
Ответ: 90.
17. Сторона ромба равна 5, а диагональ равна 6. Найдите площадь ромба.
Решение.
Диагонали ромба пересекаются под углом 90° и точкой пересечения
делятся пополам. Из прямоугольного треугольника, катетами которого являются
половины диагоналей ромба, а гипотенузой — сторона ромба, по теореме Пифагора
найдем половину неизвестной диагонали: Тогда
вся неизвестная диагональ равна 8.
Площадь ромба равна половине произведения диагоналей:
Ответ: 24.
18.
На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный
треугольник. Найдите длину его большего катета.
Решение.
Из рисунка видно, что длина катетов равна 5 и 6. Следовательно,
наибольший катет имеет длину 6.
Ответ: 6
19. Какие из следующих утверждений верны?
1. Через точку, не лежащую на данной прямой, можно провести
прямую, параллельную этой прямой.
2. В тупоугольном треугольнике все углы тупые.
3. Любой квадрат является прямоугольником.
В
ответ запишите номера выбранных утверждений без пробелов, запятых и других
дополнительных символов.
Решение.
Рассмотрим каждое из утверждений:
1. Через точку, не лежащую на данной прямой, можно провести
прямую, параллельную этой прямой — верно.
2. В тупоугольном треугольнике все углы тупые — неверно,
в тупоугольном треугольнике только один из углов тупой.
3. Любой квадрат является прямоугольником — верно,
квадрат есть частный случай прямоугольника.
Ответ: 13
20. Найдите значение выражения если
Решение.
Найдём значение выражения
Поэтому
Ответ: 1.
21. Из городов А и В навстречу друг другу одновременно выехали
мотоциклист и велосипедист. Мотоциклист приехал в В на 42 минуты раньше, чем
велосипедист приехал в А, а встретились они через 28 минут после выезда.
Сколько часов затратил на путь из В в А велосипедист?
Решение.
Пусть — скорость мотоциклиста,
—
скорость велосипедиста. Примем расстояние между городами за единицу.
Мотоциклист и велосипедист встретились через 28 минут, то есть через часа, после выезда,
поэтому Мотоциклист
прибыл в B на 42 минуты раньше, чем велосипедист в А, откуда Получаем
систему уравнений:
Скорость мотоциклиста не может быть отрицательной, поэтому
скорость велосипедиста равна , а
время, затраченное на весь путь равно 1,4 часа.
Ответ: 1,4.
22. Найдите все значения , при которых неравенство
не имеет
решений.
Решение.
График функции — парабола, ветви
которой направлены вверх. Значит, данное неравенство не имеет решений в том и
только том случае, когда эта парабола целиком расположена в верхней полуплоскости.
Отсюда следует, что дискриминант квадратного трёхчлена должен быть
отрицателен.
Найдем четверть дискриминанта: Полученный
квадратный трехчлен отрицателен при
Ответ:
23.
Найдите угол АСО, если его сторона СА касается
окружности, О — центр окружности, а дуга AD окружности,
заключённая внутри этого угла, равна 100°
Решение.
Проведём радиус в точку касания. Так как
—
радиус, а — касательная, то
Угол
— центральный, следовательно, он
равен величине дуги, на которую опирается, Угол
—
развёрнутый, следовательно,
Из треугольника
Ответ: 10°.
24. В параллелограмме ABCD диагонали AC и BD пересекаются
в точке K. Докажите, что площадь параллелограмма ABCD в
четыре раза больше площади треугольника AKB.
Решение.
Проведём высоту так, чтобы она проходила через
точку Углы
и
равны
друг другу как вертикальные. Вспомним также, что диагонали делятся точкой
пересечения пополам, следовательно, Рассмотрим
треугольники и
, они прямоугольные,
имеют равные углы и равные гипотенузы, следовательно, эти треугольники равны, а
значит равны отрезки и
. Таким образом,
Площадь параллелограмм равна а
площадь треугольника
25. На стороне BC остроугольного треугольника ABC (AB≠AC)
как на диаметре построена полуокружность, пересекающая высоту AD в
точке M, AD = 15, MD = 3, H —
точка пересечения высот треугольника ABC. Найдите AH.
Решение.

построения и введём обозначения как указано на рисунке. Угол —
вписанный, опирающийся на диаметр, поэтому он равен 90°. Значит, точка
пересечения прямых и
— точка пересечения
высот Продолжим высоту
до
пересечения с окружностью в точке Получаем, что
По
теореме о секущих получаем, что Треугольники
и
—
прямоугольные, угол — общий, следовательно, эти
треугольники подобны, откуда:
Ответ: 14,4.
Задача впр 5 класс математика про гостиницу
Задание 5 № 368425
Фирма выбирает место для строительства гостиницы: в центре города или на его окраине. Стоимость прокладки 1 метра коммуникаций равна 5500 рублей. В гостинице планируется сдавать 500 номеров. Стоимость земли, цена строительства гостиницы и средняя стоимость номера даны в таблице.
МестоЦена земли
| Центр | 58,2 | 136 | 200 | 3200 |
| Окраина | 11,3 | 128 | 2800 | 2800 |
(млн руб.)Цена
Строительства
(млн руб.)Длина
Коммуникаций
(м)Стоимость
Номера
(руб./сутки)
Обдумав оба варианта, компания выбрала местом для строительства центр города. Через сколько суток после начала сдачи номеров (при условии полной загрузки гостиницы) более высокая стоимость номеров компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций?
На плане (см. рисунок) изображён район города, в котором проживает Вика. Сторона каждой клетки на плане равна 15 м. Рядом с домом Вики, обозначенным на плане цифрой 4, находится одноэтажный магазин площадью 900 м 2 и фитнес‐центр. В 15 м от магазина расположен дом, где живёт одноклассник Вики Артём. В 30 м от детской площадки находится дом, где живёт Олег. Если выйти из фитнес‐центра, пройти небольшой ельник, обозначенный цифрой 6, и детскую площадку, то приходишь к угловому дому, где живёт дедушка Вики. Рядом с ним находится мастерская по ремонту бытовой техники. Через дорогу от дома дедушки расположен рынок, а недалеко от него – мебельный центр площадью 20250 м 2 .
Задание 1 № 368420
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
Объекты
| Магазин | Фитнес‐центр | Мастерская | Дом, где живёт Олег |
Цифры
Рядом с домом Вики, обозначенным на плане цифрой 4, находится одноэтажный магазин площадью 900 м 2 и фитнес‐центр. Значит, магазин отмечен цифрой 7, а фитнес-центр — цифрой 5. 30 м от детской площадки находится дом, где живёт Олег. Следовательно, дом, где живёт Олег, обозначен цифрой 1. Если выйти из фитнес‐центра, пройти небольшой ельник, обозначенный цифрой 6, и детскую площадку, то приходишь к угловому дому, где живёт дедушка Вики. Рядом с ним находится мастерская по ремонту бытовой техники. Значит, мастерская отмечена цифрой 2.
Задание 1 № 368420
Задание 5 № 368425
Цена строительства млн руб.
Oge. sdamgia. ru
22.08.2018 21:34:29
2018-08-22 21:34:29
Источники:
Https://oge. sdamgia. ru/problem? id=368425
ВПР–2022, математика–5: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Задача впр 5 класс математика про гостиницу
Задача впр 5 класс математика про гостиницу
Задача впр 5 класс математика про гостиницу

Задание 14 № 9155
В гостинице имеются одноместные, двухместные и трёхместные номера. Всего номеров 14, а всего мест во всех номерах 25. Одноместных номеров столько, сколько двухместных и трёхместных вместе. Сколько в гостинице трёхместных номеров?
По условию, половина всех номеров — одноместные, то есть 14 : 2 = 7 номеров. В остальных 7 номерах 25 − 7 = 18 мест. Пусть в гостинице X двухместных номеров, тогда трехместных — 7 − X. Решим уравнение 2X + (7 − X) · 3 = 18, откуда X = 3. Значит, в гостинице три двухместных номера и четыре трехместных.
Задание 14 № 9155
По условию, половина всех номеров одноместные, то есть 14 2 7 номеров.
Math5-vpr. sdamgia. ru
31.05.2019 8:31:41
2019-05-31 08:31:41
Источники:
Https://math5-vpr. sdamgia. ru/problem? id=9155
ВПР–2022, математика–5: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Задача впр 5 класс математика про гостиницу
Задача впр 5 класс математика про гостиницу
Задача впр 5 класс математика про гостиницу
Задание 14 № 2044
В гостинице имеются одноместные, двухместные и трёхместные номера. Всего номеров 12, а всего мест во всех номерах 23. Одноместных номеров столько, сколько двухместных и трёхместных вместе. Сколько в гостинице двухместных номеров?
Запишите решение и ответ.
Пусть одноместных — х номеров, двухместных — у номеров, трехместных — z номеров. Тогда имеем:
Отсюда получаем, что 2 · х = 12. Таким образом, х = 6 номеров одноместных. Значит, 23 − 6 = 17 мест в двухместных и трехместных номерах. Имеем:
Задание 14 № 2044
Тогда имеем.
Math5-vpr. sdamgia. ru
07.10.2018 9:57:26
2018-10-07 09:57:26
Источники:
Https://math5-vpr. sdamgia. ru/problem? id=2044
ПОДЕЛИТЬСЯ
Новый сентябрьский тренировочный вариант (тренировочная работа) №37446019 решу ОГЭ 2022 года по математике 9 класс с ответами и решением для подготовки к экзамену, вариант составлен по новой демоверсии ФИПИ.
Ссылка для скачивания варианта: задания (КИМ)
Ответы и решения для варианта: скачать
Решу ОГЭ 2022 по математике 9 класс тренировочный вариант №37446019
Ответы и решения для заданий ОГЭ 2022
На плане (см. рисунок) изображён район города, в котором проживает Вика. Сторона каждой клетки на плане равна 15 м. Рядом с домом Вики, обозначенным на плане цифрой 4, находится одноэтажный магазин площадью 900 м 2 и фитнес‐ центр. В 15 м от магазина расположен дом, где живёт одноклассник Вики Артём. В 30 м от детской площадки находится дом, где живёт Олег. Если выйти из фитнес‐центра, пройти небольшой ельник, обозначенный цифрой 6, и детскую площадку, то приходишь к угловому дому, где живёт дедушка Вики. Рядом с ним находится мастерская по ремонту бытовой техники. Через дорогу от дома дедушки расположен рынок, а недалеко от него – мебельный центр площадью 2025 м 2 .
Задание 1 №368420 Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
Правильный ответ: 7521
Задание 2 №368421 Детскую площадку решили покрыть резиновой плиткой размером 1 м × 1 м каждая. Плитка продаётся упаковками по 16 штук. Какое минимальное количество упаковок плитки необходимо приобрести?
Правильный ответ: 352
Задание 3 №368422 Найдите суммарную площадь, которую занимают магазин и фитнес-центр. Ответ дайте в м 2 .
Правильный ответ: 2700
Задание 4 №368424 По периметру детской площадки планируется поставить забор. Найдите его длину (в метрах).
Правильный ответ: 300
Задание 5 №368425 Фирма выбирает место для строительства гостиницы: в центре города или на его окраине. Стоимость прокладки 1 метра коммуникаций равна 5500 рублей. В гостинице планируется сдавать 500 номеров. Стоимость земли, цена строительства гостиницы и средняя стоимость номера даны в таблице. Обдумав оба варианта, компания выбрала местом для строительства центр города. Через сколько суток после начала сдачи номеров (при условии полной загрузки гостиницы) более высокая стоимость номеров компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций?
Правильный ответ: 203
Задание 10 №316354 Фирма «Вспышка» изготавливает фонарики. Вероятность того, что случайно выбранный фонарик из партии бракованный, равна 0,02. Какова вероятность того, что два случайно выбранных из одной партии фонарика окажутся небракованными?
Правильный ответ: 0,9604
Задание 14 №393946 Васе надо решить 434 задачи. Ежедневно он решает на одно и то же количество задач больше по сравнению с предыдущим днем. Известно, что за первый день Вася решил 5 задач. Определите, сколько задач решил Вася в последний день, если со всеми задачами он справился за 14 дней.
Правильный ответ: 57
Задание 15 №323537 Диагональ прямоугольника образует угол 51° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Правильный ответ: 78
Задание 16 №348379 Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 30°. Ответ дайте в градусах.
Правильный ответ: 60
Задание 17 №311480 Средняя линия трапеции равна 11, а меньшее основание равно 5. Найдите большее основание трапеции.
Правильный ответ: 17
Задание 18 №341709 На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его высоты, опущенной на сторону AC.
Правильный ответ: 4
Задание 19 №341332 Какое из следующих утверждений верно? 1) Диагонали параллелограмма равны. 2) Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне. 3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
Правильный ответ: 2
Задание 21 №338603 Первые 5 часов автомобиль ехал со скоростью 60 км/ч, следующие 3 часа — со скоростью 100 км/ч, а последние 4 часа — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Правильный ответ: 75
Задание 24 №333131 Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади параллелограмма.
Задание 25 №315126 Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Найдите длину стороны AC, если радиус описанной окружности треугольника ABC равен 7.
Правильный ответ: 14
Другие тренировочные варианты ОГЭ 2022 по математике 9 класс:
-
Тренировочный вариант №18 ОГЭ 2022 по математике 9 класс с ответами
-
Тренировочный вариант Ларина №290 ОГЭ 2022 по математике 9 класс
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Магазин | Фитнес‐центр | Мастерская | Дом, где живёт Олег |
|---|---|---|---|---|
| Цифры |
На плане (см. рисунок) изображён район города, в котором проживает Вика. Сторона каждой клетки на плане равна 15 м. Рядом с домом Вики, обозначенным на плане цифрой 4, находится одноэтажный магазин площадью 900 м2 и фитнес‐центр. В 15 м от магазина расположен дом, где живёт одноклассник Вики Артём. В 30 м от детской площадки находится дом, где живёт Олег. Если выйти из фитнес‐центра, пройти небольшой ельник, обозначенный цифрой 6, и детскую площадку, то приходишь к угловому дому, где живёт дедушка Вики. Рядом с ним находится мастерская по ремонту бытовой техники. Через дорогу от дома дедушки расположен рынок, а недалеко от него – мебельный центр площадью 2025 м2.
1
Детскую площадку решили покрыть резиновой плиткой размером 1 м × 1 м каждая. Плитка продаётся упаковками по 16 штук. Какое минимальное количество упаковок плитки необходимо приобрести?
Источник: Тренировочный вариант № 232, усложнённый, Александр Ларин
2
Найдите суммарную площадь, которую занимают магазин и фитнес-центр. Ответ дайте в м2.
Источник: Тренировочный вариант № 232, усложнённый, Александр Ларин
3
По периметру детской площадки планируется поставить забор. Найдите его длину (в метрах).
Источник: Тренировочный вариант № 232, усложнённый, Александр Ларин
4
Фирма выбирает место для строительства гостиницы: в центре города или на его окраине. Стоимость прокладки 1 метра коммуникаций равна 5500 рублей. В гостинице планируется сдавать 500 номеров. Стоимость земли, цена строительства гостиницы и средняя стоимость номера даны в таблице.
| Место | Цена земли (млн руб.) |
Цена строительства (млн руб.) |
Длина коммуникаций (м) |
Стоимость номера (руб./сутки) |
|---|---|---|---|---|
| Центр | 58,2 | 136 | 200 | 3200 |
| Окраина | 11,3 | 128 | 2800 | 2800 |
Обдумав оба варианта, компания выбрала местом для строительства центр города. Через сколько суток после начала сдачи номеров (при условии полной загрузки гостиницы) более высокая стоимость номеров компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций?
Источник: Тренировочный вариант № 232, усложнённый, Александр Ларин
Спрятать решение
Решение.
Рядом с домом Вики, обозначенным на плане цифрой 4, находится одноэтажный магазин площадью 900 м2 и фитнес‐центр. Значит, магазин отмечен цифрой 7, а фитнес-центр — цифрой 5. 30 м от детской площадки находится дом, где живёт Олег. Следовательно, дом, где живёт Олег, обозначен цифрой 1. Если выйти из фитнес‐центра, пройти небольшой ельник, обозначенный цифрой 6, и детскую площадку, то приходишь к угловому дому, где живёт дедушка Вики. Рядом с ним находится мастерская по ремонту бытовой техники. Значит, мастерская отмечена цифрой 2.
Ответ: 7521.
Источник: Тренировочный вариант № 232, усложнённый, Александр Ларин
6 декабря 2022 13:02
402
компания выбирает место для строительства торгово-развлекательного комплекса:на месте квартал старых одноэтажных домов в центре города или на окраине города.стоимость прокладки 1 метра коммуникации равна 6000 руб.в аренду планирует создавать 4000 кв.м.площади комплекса.стоимость земли цена строительства комплекса с учетом сноса старых зданий и предполагаемая стоимость сдачи в аренду в таблице.обдумав оба варианта компания выбрала место для строительства центр города.Через сколько месяцев после начала сдачи в аренду торговых площадей построенного комплекса более высокая стоимость аренды компенсирует разность в стоимости земли,строительство и прокладывания коммуникаций,если компания платит налог 13% стоимости,полученных за сдачу в аренду?Ответ округлите до целых.
Посмотреть ответы
1 млн = 1 000 000
1)
6 000 · 200 = 1 200 000 (руб.) — стоимость прокладки коммуникаций в центре;
1 200 000 руб. = 1,2 млн руб.;
64,4 + 176 + 1,2 = 241,6 (млн руб.) —
затраты на постройку ТРК в центре
.
2)
6 000 · 3 500 = 21 000 000 (руб.) — стоимость прокладки коммуникаций на окраине;
21 000 000 руб. = 21 млн руб.;
11,2 + 168 + 21 = 200,2 (млн руб.) —
затраты на постройку ТРК на окраине
.
3)
241,6 — 200,2 = 41,4 (млн руб.) —
разность в стоимости земли, строительства и прокладывания коммуникаций
.
4)
1 200 — 900 = 300 (руб./месяц) — разность в стоимости аренды за 1 м².
После уплаты налога в 13% аренда принесёт 100%-13%=87% от прибыли без налогов.
1% от чего-то составляет 0,01 долю от того же.
300 · 0,87 = 261 (руб./месяц) — разность в стоимости аренды за 1 м², с учётом уплаты налогов.
261 · 4 000 = 1 044 000 (руб./месяц) —
разность в стоимости аренды за 4 000 м², с учётом уплаты налогов
.
1 044 000 руб./месяц = 1,044 млн руб./месяц
5) (мес.) — время за которое компенсируется разность.
Ответ
: 40.
Еще вопросы по категории Математика
1 млн = 1 000 000
1)
6 000 · 200 = 1 200 000 (руб.) — стоимость прокладки коммуникаций в центре;
1 200 000 руб. = 1,2 млн руб.;
64,4 + 176 + 1,2 = 241,6 (млн руб.) — затраты на постройку ТРК в центре.
2)
6 000 · 3 500 = 21 000 000 (руб.) — стоимость прокладки коммуникаций на окраине;
21 000 000 руб. = 21 млн руб.;
11,2 + 168 + 21 = 200,2 (млн руб.) — затраты на постройку ТРК на окраине.
3)
241,6 — 200,2 = 41,4 (млн руб.) — разность в стоимости земли, строительства и прокладывания коммуникаций.
4)
1 200 — 900 = 300 (руб./месяц) — разность в стоимости аренды за 1 м².
После уплаты налога в 13% аренда принесёт 100%-13%=87% от прибыли без налогов.
1% от чего-то составляет 0,01 долю от того же.
300 · 0,87 = 261 (руб./месяц) — разность в стоимости аренды за 1 м², с учётом уплаты налогов.
261 · 4 000 = 1 044 000 (руб./месяц) — разность в стоимости аренды за 4 000 м², с учётом уплаты налогов.
1 044 000 руб./месяц = 1,044 млн руб./месяц
5)
(мес.) — время за которое компенсируется разность.
Ответ: 40.
Приложения: