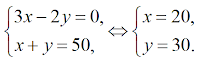Нефтяная компания бурит скважину для добычи нефти которая залегает по данным геологоразведки на 3 км

Спрятать решение

Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко. 2015 г.

Формулировка задачи: Нефтяная компания бурит скважину для добычи нефти, которая залегает, по данным геологоразведки, на глубине N км. В течение рабочего дня бурильщики проходят L метров в глубину, но за ночь скважина вновь «заиливается», то есть заполняется грунтом на K метров. За сколько рабочих дней нефтяники пробурят скважину до глубины залегания нефти?

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 20 (Задачи на смекалку).

Рассмотрим, как решаются подобные задачи на примере.

В
ЕГЭ базового уровня есть задача на
смекалку под №20. Большинство таких
задач решаются довольно просто.
Распределим задачи, представленные в
открытом банке ЕГЭ по типам и дадим им
условное название:

Тип 1. (про кузнечика) Тип 2. (про улитку) Тип 3. (с квартирами) Тип 4. (с монетами) Тип 5. (про работу) Тип 6. (про грибы) Тип 7. (про палку) Тип 8. (про лекарства)	Тип 9. (о продажах) Тип 10. (с глобусом) Тип 11. (с прямоугольником) Тип 12. (про числа) Тип 13. (с ящиками) Тип 14. (с таблицей) Тип 15. (про викторину) Тип 16. (про кольцевую дорогу)
Тип 17 (разные задачи на смекалку)

Рассмотрим
первые четыре типа.

Тип
1.  

Кузнечик прыгает
вдоль координатной прямой в любом
направлении на единичный отрезок за
один прыжок. Кузнечик начинает прыгать
из начала координат. Сколько существует
различных точек на координатной прямой,
в которых кузнечик может оказаться,
сделав ровно 11 прыжков?

Решение. Заметим,
что кузнечик в
итоге может
оказаться только в точках с нечётными
координатами, так как
количество прыжков, которое он делает,
нечётно. 

Максимально кузнечик может оказаться
в точках, модуль
которых не превышает
одиннадцати. Таким образом, кузнечик
может оказаться в точках: −11, −9, −7, −5,
−3, −1, 1, 3, 5, 7, 9 и 11; всего
12 точек.

Ответ:
12

Задачи
для самостоятельного решения.

• Заяц
  прыгает вдоль координатной прямой в
  любом направлении на единичный отрезок
  за прыжок. Сколько существует различных
  точек на координатной прямой, в которых
  заяц может оказаться, сделав ровно 6
  прыжков, начиная прыгать из начала
  координат?

• Воробей
  прыгает вдоль прямой в любом направлении.
  Длина прыжка равна единичному отрезку.
  Сколько существует точек, в которых
  воробей может оказаться, сделав 5 прыжков?

• Кузнечик
  прыгает вдоль координатной прямой в
  любом направлении на единичный отрезок
  за прыжок. Сколько существует различных
  точек на координатной прямой, в которых
  кузнечик может оказаться, сделав ровно
  12 прыжков, начиная прыгать из начала
  координат?

Тип
2.

Задача
1.Улитка за день заползает вверх по
дереву на 4 м, а за ночь сползает на 3 м.
Высота дерева 10 м. За сколько дней улитка
впервые доползёт до вершины дерева?

Решение.
За день улитка заползёт на 4 метра, а за
ночь — сползёт на 3 метра. Итого за сутки
она заползёт на метр. За шестеро суток
она поднимется на высоту шести метров.
И днём следующего дня она уже окажется
на вершине дерева.

Ответ:
7

Задача
2. Нефтяная компания бурит скважину для
добычи нефти, которая залегает, по данным
геологоразведки, на глубине 3 км. В
течение рабочего дня бурильщики проходят
300 метров в глубину, но за ночь скважина
вновь «заиливается», то есть заполняется
грунтом на 30 метров. За сколько рабочих
дней нефтяники пробурят скважину до
глубины залегания нефти?

Решение.
За день скважина увеличивается на 300 −
30 = 270 м. К началу одиннадцатого рабочего
дня нефтяники пробурят 2700 метров. За
одиннадцатый рабочий день нефтяники
пробурят ещё 300 метров, то есть дойдут
до глубины 3 км. 

Ответ: 11

Задача
3. В результате паводка котлован заполнился
водой до уровня 2 метра. Строительная
помпа непрерывно откачивает воду,
понижая её уровень на 20 см в час.
Подпочвенные воды, наоборот, повышают
уровень воды в котловане на 5 см в час.
За сколько часов работы помпы уровень
воды в котловане опустится до 80 см?

Решение.
За
час уровень воды в котловане уменьшается
на 20 − 5 = 15 см. Нужно откачать 2 · 100
− 80 = 120 см воды. Следовательно, уровень
воды в котловане опустится до 80 см за 120
: 15 = 8 часов.

Ответ:
8

Задача
4. В бак объёмом 38 литров каждый час,
начиная с 12 часов, наливают полное ведро
воды объёмом 8 литров. Но в днище бака
есть небольшая щель, и из неё за час
вытекает 3 литра. В какой момент времени
(в часах) бак будет заполнен полностью.

Решение.
К
концу каждого часа объём воды в баке
увеличивается на 8 − 3 = 5 литров. Через
6 часов, то есть в 18 часов, в баке будет
30 литров воды. В 18 часов в бак дольют 8
литров воды и объём воды в баке станет
равным 38 литров.

Ответ:
18

Решите
самостоятельно.

• Улитка
  за день заползает вверх по дереву на 4
  м, а за ночь сползает на 1 м. Высота дерева
  13 м. За сколько дней улитка впервые
  доползёт до вершины дерева?

• Улитка
  за день заползает вверх по дереву на 4
  м, а за ночь сползает на 2 м. Высота дерева
  26 м. За сколько дней улитка впервые
  доползёт до вершины дерева?

• Улитка
  за день заползает вверх по дереву на 3
  м, а за ночь сползает на 2 м. Высота дерева
  28 м. За сколько дней улитка впервые
  доползёт до вершины дерева?

Тип
3.

Задача
1. Саша пригласил Петю в гости, сказав,
что живёт в седьмом подъезде в квартире
№ 462, а этаж сказать забыл. Подойдя к
дому, Петя обнаружил, что дом семиэтажный.
На каком этаже живёт Саша? (На всех этажах
число квартир одинаково, номера квартир
в доме начинаются с единицы.)

Решение.
Поскольку в первых 7 подъездах не меньше
462 квартир, в каждом подъезде не меньше
462 : 7 = 66 квартир. Следовательно, на каждом
из 7 этажей в подъезде не меньше 9 квартир.

Пусть
на каждой лестничной площадке по 9
квартир. Тогда в первых семи подъездах
всего 9 · 7 · 7 = 441 квартира, и квартира
462 окажется в восьмом подъезде, что
противоречит условию.

Пусть
на каждой площадке по 10 квартир. Тогда
в первых семи подъездах 10 · 7 · 7 = 490
квартир, а в первых шести — 420. Следовательно,
квартира 462 находится в седьмом подъезде.
Она в нем 42-ая по счету, поскольку на
этаже по 10 квартир, она расположена на
пятом этаже.

Если
бы на каж­дой площадке было по 11
квартир, то в первых шести подъездах
оказалось бы 11 · 7 · 6 = 462 квартиры, то
есть 462 квартира в шестом подъезде, что
противоречит условию.

Значит
Саша живёт на пятом этаже.

Ответ:
5

Задача
2. Во всех подъездах дома одинаковое
число этажей, а на каждом этаже одинаковое
число квартир. При этом число этажей в
доме больше числа квартир на этаже,
число квартир на этаже больше числа
подъездов, а число подъездов больше
одного. Сколько этажей в доме, если всего
в нём 110 квартир?

Решение.
Число квартир, этажей и подъездов может
быть только целым числом.

Заметим,
что число 110 делится на 2, 5 и 11. Следовательно,
в доме должно быть 2 подъезда, 5 квартир
и 11 этажей.

Ответ:
11

Решите
самостоятельно.

• Саша
  пригласил Петю в гости, сказав, что живёт
  в восьмом подъезде в квартире № 468, а
  этаж сказать забыл. Подойдя к дому, Петя
  обнаружил, что дом 12-тиэтажный. На каком
  этаже живёт Саша? (На всех этажах число
  квартир одинаково, номера квартир в
  доме начинаются с единицы.)

• Саша
  пригласил Петю в гости, сказав, что живёт
  в двенадцатом подъезде в квартире №
  465, а этаж сказать забыл. Подойдя к дому,
  Петя обнаружил, что дом пятиэтажный. На
  каком этаже живёт Саша? (На всех этажах
  число квартир одинаково, номера квартир
  в доме начинаются с единицы.)

• Катя
  с подружкой Леной пошли в гости к Свете,
  зная, что она живёт в 364-й квартире в 6-ом
  подъезде. Подойдя к дому, они обнаружили,
  что дом 16-тиэтажный. На каком этаже живёт
  Света? (На всех этажах число квартир
  одинаковое, номера квартир начинаются
  с единицы).

• Игорь
  решил сделать домашнее задание по
  математике с Колей и пошёл к нему домой,
  зная, что он живёт рядом с доме, в пятом
  подъезде и в 206 квартире. Подойдя к дому,
  Игорь обнаружил, что он девятиэтажный.
  На каком этаже живёт Коля? (На всех этажах
  число квартир одинаковое, номера квартир
  в доме начинаются с единицы).

• Во
  всех подъездах дома одинаковое число
  этажей, а на каждом этаже одинаковое
  число квартир. При этом число этажей в
  доме больше числа квартир на этаже,
  число квартир на этаже больше числа
  подъездов, а число подъездов больше
  одного. Сколько этажей в доме, если всего
  в нём 170 квартир?

Тип
4. 

В обменном пункте можно совершить
одну из двух операций:

• за
  2 золотых монеты получить 3 серебряных
  и одну медную;

• за
  5 серебряных монет получить 3 золотых и
  одну медную.

У
Николая были только серебряные монеты.
После нескольких посещений обменного
пункта серебряных монет у него стало
меньше, золотых не появилось, зато
появилось 50 медных. На сколько уменьшилось
количество серебряных монет у Николая?

Решение.
Пусть Николай сделал сначала х операций
второго типа, а затем у операций
первого типа. Так как после нескольких
операций золотых монет не осталось, а
количество
медных монет увеличилось на 50, составим
и решим систему уравнений:

Тогда
серебряных монет стало на 3у -5х = 90 – 100
= -10 то есть на 10 меньше.

Ответ:
10

Решите
самостоятельно.

• В
  обменном пункте можно совершить одну
  из двух операций: за
  3 золотых монеты получить 4 серебряных
  и одну медную; за
  6 серебряных монет получить 4 золотых и
  одну медную. У
  Николая были только серебряные монеты.
  После посещений обменного пункта
  серебряных монет у него стало меньше,
  золотых не появилось, зато появилось
  35 медных. На сколько уменьшилось
  количество серебряных монет у Николая?

• В
  обменном пункте можно совершить одну
  из двух операций: за
  2
  золотые
  монеты получить 3
  серебряные
  и одну медную; за
  5
  серебряных монет получить 3
  золотые
  и одну медную. У
  Андрея
  были только серебряные монеты. После
  посещений обменного пункта серебряных
  монет у него стало меньше, золотых не
  появилось, зато появилось 100
  медных. На сколько уменьшилось количество
  серебряных монет у Андрея?

Слайд 1

Задания на смекалку ЕГЭ по математике базового уровня. Задания №20 Мысиковой Юлии Александровны, ученицы 11 «А» социально-экономического класса Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа №45»

Слайд 2

Улитка на дереве Решение. Улитка за день заползает вверх по дереву на 3 м, а за ночь спускается на 2 м. Итого, за сутки она продвигается на 3 – 2 = 1 метр. За 7 суток она поднимется на 7 метров. На восьмой день она заползёт вверх еще на 3 метра и впервые окажется на высоте 7 + 3 = 10 (м), т.е. на вершине дерева. Ответ: 8 Улитка за день заползает вверх по дереву на 3 м, а за ночь спускается на 2 м. Высота дерева 10 м. За сколько дней улитка доползёт от основания до вершины дерева?

Слайд 3

Бензоколонки Решение. Начертим окружность и расположим точки (бензоколонки)так, чтобы расстояния соответствовали условию. Заметим, что все расстояния между точками А, С и D известны. АС =20, АD=30, СD=20. Отметим точку А. От точки А по часовой стрелке отметим точку С, помним, что АС=20. Теперь будем отмечать точку D, которая лежит от А на расстоянии 30, это расстояние нельзя откладывать от А по часовой стрелке, так как тогда получится расстояние между С и D равно 10, а по условию СD= 2 0 . Значит от А до D надо двигаться против часовой стрелки, отмечаем точку D. Так как СD=20, то длина всей окружности равна 20+30+20=70. Так как АВ=35, то точка В диаметрально противоположна точке А. Расстояние от С до В будет равно 35-20=15. Ответ: 15. На кольцевой дороге расположены четыре бензоколонки: A, B, C и Д. Расстояние между A и B — 35 км, между A и C — 20 км, между C и Д —20 км, между Д и A — 30 км (все расстояния измеряются вдоль кольцевой дороги в кратчайшую сторону). Найдите расстояние между B и C. Ответ дайте в километрах.

Слайд 4

В кинозале Решение. 1 способ. Просто считаем сколько мест в рядах до восьмого: 1 – 24 2 – 26 3 – 28 4 – 30 5 – 32 6 – 34 7 – 36 8 – 38. Ответ: 38. В пер­вом ряду ки­но­за­ла 24 места, а в каж­дом сле­ду­ю­щем на 2 боль­ше, чем в преды­ду­щем. Сколь­ко мест в вось­мом ряду? 2 способ. Замечаем, что количество мест в рядах составляет арифметическую прогрессию с первым члено в 24 и разность равной 2. По формуле n — го члена прогрессии находим восьмой член а 8 = 24 + (8 – 1)*2 = 38. Ответ: 38.

Слайд 5

Грибы в корзине Решение. Из условия , что среди любых 27 гри­бов име­ет­ся хотя бы один рыжик следует – количество груздей не больше 26. Из второго условия, что среди любых 25 гри­бов хотя бы один груздь, следует — количество рыжиков не больше 24. Так как всего грибов – 50, то рыжиков 24, а груздей – 26. Ответ: 24. В кор­зи­не лежат 50 гри­бов: ры­жи­ки и груз­ди. Из­вест­но, что среди любых 27 гри­бов име­ет­ся хотя бы один рыжик, а среди любых 25 гри­бов хотя бы один груздь. Сколь­ко ры­жи­ков в кор­зи­не?

Слайд 6

Кубики в ряд Решение. Если пронумеровать все кубики числами от одного до шести (не учитывая, что имеются кубики разного цвета), то получим общее число перестановки кубиков: Р(6)=6*5*4*3*2*1=720 Теперь вспомним, что имеются 2 кубика красного цвета и перестановка их местами (Р(2)=2*1=2) не даст нового способа, поэтому полученное произведение надо уменьшить в 2 раза. Аналогично, вспоминаем, что у нас имеются 3 кубика зелёного цвета, поэтому придётся полученное произведение уменьшить ещё и в 6 раз (Р(3)=3*2*1=6) Итак, получим общее число способов расстановки кубиков 60. Ответ: 60. Сколь­ки­ми спо­со­ба­ми можно по­ста­вить в ряд два оди­на­ко­вых крас­ных ку­би­ка, три оди­на­ко­вых зелёных ку­би­ка и один синий кубик?

Слайд 7

На бе­го­вой до­рож­ке Тре­нер по­со­ве­то­вал Ан­дрею в пер­вый день за­ня­тий про­ве­сти на бе­го­вой до­рож­ке 15 минут, а на каж­дом сле­ду­ю­щем за­ня­тии уве­ли­чи­вать время, про­ведённое на бе­го­вой до­рож­ке, на 7 минут. За сколь­ко за­ня­тий Ан­дрей про­ведёт на бе­го­вой до­рож­ке в общей слож­но­сти 2 часа 25 минут, если будет сле­до­вать со­ве­там тре­не­ра? Решение. 1 способ. Замечаем, что надо найти сумму арифметической прогрессии с первым членом 15 и разность равной 7. По формуле суммы n первых членов прогрессии S n =(2a 1 +(n-1)d)*n/2 имеем 145=(2*15+(n–1)*7)*n/2, 290=(30+(n–1)*7)*n, 290=(30+7n–7)*n, 290=(23+7n)*n, 290=23n+7n 2 , 7n 2 +23n-290=0, n=5 . Ответ: 5. 2 способ. Более трудоёмкий. 1-15-15 2-22-37 3-29-66 4-36-102 5-43-145. Ответ: 5.

Слайд 8

Меняем монеты За­да­ние 20. В об­мен­ном пунк­те можно со­вер­шить одну из двух опе­ра­ций: за 2 зо­ло­тые мо­не­ты по­лу­чить 3 се­реб­ря­ные и одну мед­ную; за 5 се­реб­ря­ных монет по­лу­чить 3 зо­ло­тые и одну мед­ную. У Ни­ко­лая были толь­ко се­реб­ря­ные мо­не­ты. После не­сколь­ких по­се­ще­ний об­мен­но­го пунк­та се­реб­ря­ных монет у него стало мень­ше, зо­ло­тых не по­яви­лось, зато по­яви­лось 50 мед­ных. На сколь­ко умень­ши­лось ко­ли­че­ство се­реб­ря­ных монет у Ни­ко­лая? Решение. Пусть Николай сделал сначала х операций второго типа, а затем у операций первого типа. Тогда имеем: Тогда серебряных монет стало на 3у -5х = 90 – 100 = -10 т.е. на 10 меньше . Ответ: 10

Слайд 9

Хозяин договорился Решение. Из условия понятно, что по­сле­до­ва­тель­ность цен за каждый выкопанный метр является ариф­ме­ти­че­ской про­грес­сией с пер­вым чле­ном а 1 = 3700 и раз­но­стью d=1700 . Сумма пер­вых n чле­нов ариф­ме­ти­че­ской про­грес­сии вы­чис­ля­ет­ся по фор­му­ле S n = 0,5(2a 1 + (n – 1)d)n . Подставляя исходные данные, получаем: S 10 = 0,5(2*3700 + (8 – 1)*1700)*8 = 77200 . Таким образом, хо­зя­ин дол­жен будет за­пла­тить ра­бо­чим 77200 руб. Ответ: 77200. Хозяин договорился с рабочими, что они выкопают ему колодец на следующих условиях: за первый метр он заплатит им 3700 рублей, а за каждый следующий метр — на 1700 рублей больше, чем за предыдущий. Сколько денег хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 8 метров?

Слайд 10

Вода в котловане В ре­зуль­та­те па­вод­ка кот­ло­ван за­пол­нил­ся водой до уров­ня 2 метра. Стро­и­тель­ная помпа не­пре­рыв­но от­ка­чи­ва­ет воду, по­ни­жая её уро­вень на 20 см в час. Под­поч­вен­ные воды, на­о­бо­рот, по­вы­ша­ют уро­вень воды в кот­ло­ва­не на 5 см в час. За сколь­ко часов ра­бо­ты помпы уро­вень воды в кот­ло­ва­не опу­стит­ся до 80 см? Решение. В результате работы насоса и подтопления почвенными водами уровень воды в котловане понижается на 20-5=15 сантиметров за час. Чтобы уровень снизился на 200-80=120 сантиметров необходимо 120:15=8 часов. Ответ: 8.

Слайд 11

Бак с щелью В бак объёмом 38 литров каждый час, начиная с 12 часов, наливают полное ведро воды объёмом 8 литров. Но в днище бака есть небольшая щель, и из неё за час вытекает 3 литра. В какой момент времени (в часах) бак будет заполнен полностью? Решение. К концу каждого часа объём воды в баке увеличивается на 8 − 3 = 5 литров. Через 6 часов, то есть в 18 часов, в баке будет 30 литров воды. В 19 часов в бак дольют 8 литров воды и объём воды в баке станет равным 38 литров. Ответ: 19.

Слайд 12

Скважина Неф­тя­ная ком­па­ния бурит сква­жи­ну для до­бы­чи нефти, ко­то­рая за­ле­га­ет, по дан­ным гео­ло­го­раз­вед­ки, на глу­би­не 3 км. В те­че­ние ра­бо­че­го дня бу­риль­щи­ки про­хо­дят 300 мет­ров в глу­би­ну, но за ночь сква­жи­на вновь «за­или­ва­ет­ся», то есть за­пол­ня­ет­ся грун­том на 30 мет­ров. За сколь­ко ра­бо­чих дней неф­тя­ни­ки про­бу­рят сква­жи­ну до глу­би­ны за­ле­га­ния нефти? Решение. Учитывая заиливание скважины, в течении суток проходят 300-30=270 метров. Значит за 10 полных суток будет пройдено 2700 метров и за 11-й рабочий день будет пройдено ещё 300 метров. Ответ: 11.

Слайд 13

Глобус На по­верх­но­сти гло­бу­са фло­ма­сте­ром про­ве­де­ны 17 па­рал­ле­лей и 24 ме­ри­ди­а­на. На сколь­ко ча­стей про­ведённые линии раз­де­ли­ли по­верх­ность гло­бу­са? Решение. Одна параллель разбивает поверхность глобуса на 2 части. Две на три части. Три на четыре части и т. д. 17 параллелей разбивают поверхность на 18 частей. Проведём один меридиан, и получим одну целую (не разрезанную) поверхность. Проведём второй меридиан и у нас уже две части, третий меридиан разобьёт поверхность на три части и т. д. 24 меридиана разбили нашу поверхность на 24 части. Получаем 18*24=432. Все линии разделят поверхность глобуса на 432 части. Ответ: 432.

Слайд 14

Кузнечик прыгает Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 8 прыжков, начиная прыгать из начала координат? Решение: Немного подумав, мы можем за­ме­тить, что куз­не­чик может ока­зать­ся толь­ко в точ­ках с чётными ко­ор­ди­на­та­ми, по­сколь­ку число прыж­ков, ко­то­рое он де­ла­ет, чётно. Например, если он сделает пять прыжков в одну сторону, то в обратную сторону он сделает три прыжка и окажется в точках 2 или −2. Мак­си­маль­но куз­не­чик может ока­зать­ся в точ­ках, мо­дуль ко­то­рых не пре­вы­ша­ет восьми. Таким об­ра­зом, куз­не­чик может ока­зать­ся в точ­ках: −8, −6, −4, −2, 0, 2, 4, 6 и 8; всего 9 точек. Ответ: 9 .

Слайд 15

Новые бактерии Каж­дую се­кун­ду бак­те­рия де­лит­ся на две новые бак­те­рии. Из­вест­но, что весь объём од­но­го ста­ка­на бак­те­рии за­пол­ня­ют за 1 час. За сколь­ко се­кунд бак­те­рии за­пол­ня­ют по­ло­ви­ну ста­ка­на? Решение. Вспомним, что 1 час = 3600 секундам. Через каждую секунду бактерий становится в два раза больше. Значит, чтобы из половины стакана бактерий получился полный стакан нужна всего 1 секунда. Поэтому стакан был заполнен на половину за 3600-1=3599 секунд. Ответ: 3599.

Слайд 16

Делим числа Про­из­ве­де­ние де­ся­ти иду­щих под­ряд чисел раз­де­ли­ли на 7. Чему может быть равен оста­ток? Решение. Задача простая, так как среди десяти подряд идущих натуральных чисел хотя бы одно делится на 7. Значит и всё произведение будет делиться на 7 без остатка. То есть остаток равен 0. Ответ: 0.

Слайд 17

Где живёт Петя? Задача 1. В доме, в котором живёт Петя, один подъезд. На каждом этаже по шесть квартир. Петя живёт в квартире № 50. На каком этаже живёт Петя? Решение: Делим 50 на 6, получаем частное 8 и 2 в остатке. Это значит, что Петя живёт на 9 этаже. Ответ: 9. Задача 2. Во всех подъездах дома одинаковое число этажей, и на всех этажах одинаковое число квартир. При этом число этажей в доме больше числа квартир на этаже, число квартир на этаже больше числа подъездов, а число подъездов больше одного. Сколько этажей в доме, если всего в нём 455 квартир? Решение: Решение этой задачи вытекает из разложения числа 455 на простые множители. 455 = 13*7*5. Значит в доме 13 этажей, по 7 квартир на каждом этаже в подъезде, 5 подъездов. Ответ: 13.

Слайд 18

Задача 3. Саша пригласил Петю в гости, сказав, что живёт в восьмом подъезде в квартире № 468, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом двенадцатиэтажный. На каком этаже живёт Саша? (На всех этажах число квартир одинаково, номера квартир в доме начинаются с единицы.) Решение: Петя может подсчитать, что в двенадцатиэтажном доме в первых семи подъездах 12*7=84 площадки. Дальше, перебирая возможное количество квартир на одной площадке, можно увидеть, что их меньше шести, так как 84*6 = 504. Это больше 468. Значит , на каждой из площадок 5 квартир, тогда в первых семи подъездах 84*5 =420 квартир. 468 – 420 = 48, то есть Саша живёт в 48 квартире в 8 подъезде (если бы нумерация была с единицы в каждом подъезде). 48:5 = 9 и 3 в остатке. Таким образом Сашина квартира на 10 этаже. Ответ: 10.

Слайд 19

Меню ресторана В меню ресторана имеется 6 видов салатов, 3 вида первых блюд, 5 видов вторых блюд и 4 вида десерта. Сколько вариантов обеда из салата, первого, второго и десерта могут выбрать посетители этого ресторана? Решение. Если мы пронумеруем каждый салат, первое, второе, десерт, то: с 1 салатом, 1 первым,1 вторым можно подать один из 4-х десертов. 4 варианта. Со вторым вторым тоже 4 варианта и т.д. Всего получим 6*3*5*4=360. Ответ: 360.

Слайд 20

Маша и медведь Медведь съел свою половину банки варенья в 3 раза быстрее, чем Маша, значит, у него еще осталось в 3 раза больше времени на кушанье печенья. Т.к. Медведь ест печенье в 3 раза быстрее, чем Маша и еще у него осталось в 3 раза больше времени (он съел в 3 раза быстрее свою половину банки варенья), то он съедает в 3⋅3=9 раз больше печений, чем Маша (9 печений съедает Медведь, в то время как Маша только 1 печенье). Получается, что в отношении 9:1 едят Медведь и Маша печенье. Всего получается 10 долей, значит, 1 доля равна 160:10=16. В итоге, Медведь съел 16⋅9=144 печений. Ответ: 144 Маша и Медведь съели 160 печений и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь — печенье, но в какой-то момент они поменялись. Медведь и то, и другое ест в три раза быстрее Маши. Сколько печений съел Медведь, если варенье они съели поровну?

Слайд 21

Палки и линии На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 15 кусков, если по жёлтым — 5 кусков, а если по зелёным — 7 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов? Решение. Если распилить палку по красным линиям, то получится 15 кусков, следовательно, линий — 14. Если распилить палку по желтым — 5 кусков, следовательно, линий — 4. Если распилить по зеленым — 7 кусков, линий — 6. Всего линий: 14+4+6=24 линии, следовательно, кусков будет 25. Ответ: 25

Слайд 22

Врач прописал Врач прописал пациенту принимать лекарство по такой схеме: в первый день он должен принять 3 капли, а в каждый следующий день — на 3 капли больше, чем в предыдущий. Приняв 30 капель, он ещё 3 дня пьёт по 30 капель лекарства, а потом ежедневно уменьшает приём на 3 капли. Сколько пузырьков лекарства нужно купить пациенту на весь курс приёма, если в каждом содержится 20 мл лекарства (что составляет 250 капель )? Решение На первом этапе приёма капель число принимаемых капель в день представляет собой возрастающую арифметическую прогрессию с первым членом, равным 3, разностью, равной 3 и последним членом, равным 30. Следовательно: Тогда 3 + 3( n -1)=30; 3+ 3 n -3=30; 3 n =30; n =10 , т.е. прошло 10 дней по схеме увеличения до 30 капель. Знаем формулу суммы ариф . прогрессии: Вычислим S10 :

Слайд 23

За следующие 3 дня – по 30 капель: 30 · 3 = 90 (капель) На последнем этапе приёма: Т.е. 30 -3( n-1 ) =0; 30 -3n+3=0; -3n=-33; n=11 т.е. 11 дней приём лекарства уменьшался. Найдём сумму арифметич . прогрессии 4) Значит, 165 + 90 + 165 = 420 капель всего 5) Тогда 420 : 250 = 42/25 = 1 (17/25) пузырька Ответ: надо купить 2 пузырька

Слайд 24

Магазин бытовой техники В магазине бытовой техники объём продаж холодильников носит сезонный характер. В январе было продано 10 холодильников, и в три последующих месяца продавали по 10 холодильников. С мая продажи увеличивались на 15 единиц по сравнению с предыдущим месяцем. С сентября объём продаж начал уменьшаться на 15 холодильников каждый месяц относительно предыдущего месяца. Сколько холодильников продал магазин за год? Решение. Последовательно рассчитаем сколько холодильников было продано за каждый месяц и просуммируем результаты: 10 · 4+(10+15)+(25+15)+(40+15 )+( 55+15)+(70-15)+ (55-15 )+( 40-15)+ ( 25-15 )= = 40+25+40+55+70+55+40+25+10=120+110+130=360 Ответ: 360.

Слайд 25

Ящики Ящики двух видов, имеющие одинаковую ширину и высоту, укладывают на складе в один ряд длиной 43м, приставляя друг к другу по ширине. Ящики одного вида имеют длину 2м, а другого-5м. Какое наименьшее число ящиков потребуется для заполнения всего ряда без образования пустых мест? Решение Т.к . надо найти наименьшее число ящиков, то => надо взять наибольшее количество больших ящиков. Значит 5 · 7 = 35; 43 – 35 = 8 и 8:2=4 ; 4+7=11 Значит, ящиков всего 11 . Ответ: 11.

Слайд 26

Таблица В таблице три столбца и несколько строк. В каждую клетку таблицы поставили по натуральному числу так, что сумма всех чисел в первом столбце равна 119, во втором — 125, в третьем — 133, а сумма чисел в каждой строке больше 15, но меньше 18. Сколько всего строк в столбце? Решение. Общая сумма во всех столбцах = 119 + 125 + 133 = 377 Числа 18 и 15 не включены в предел, значит: 1) если сумма в строке = 17, то, количество строк равно 377 : 17= =22,2 2) если сумма в строке = 16, то, количество строк равно 377 : 16= =23,5 Значит кол-во строк = 23 (т.к. оно должно быть между 22,2 и 23,5 ) Ответ: 23

Слайд 27

Викторина и задания Список заданий викторины состоял из 36 вопросов. За каждый правильный ответ ученик получал 5 очков, за неправильный ответ с него списывали 11 очков, а при отсутствие ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 75 очков, если известно, что по крайней мере один раз он ошибся? Решение. 1 способ: Пусть Х – количество верных ответов у – количество неверных ответов. Тогда составим уравнение 5х -11у = 75, где 0 < х < 36 и 0 < у < 36 . Из уравнения видно, что у делится на 5. Пусть: 1) у=5, тогда 5х = 75 + 11у= 75 + 55=130, тогда х = 130 : 5 = 26 и это меньше 36. 2) у=10, тогда 5х =75 +11у=75+110=185, тогда х = 185 : 5=37, но это больше 36 . Ответ:26 2 способ: 36 вопросов — 11 очков за неправильный ответ + 1 = 26 очков

Слайд 28

Группа туристов Группа туристов преодолела горный перевал. Первый километр подъёма они преодолели за 50 минут, а каждый следующий километр проходили на 15 минут дольше предыдущего. Последний километр перед вершиной был пройден за 95 минут. После десятиминутного отдыха на вершине туристы начали спуск, который был более пологим. Первый километр после вершины был пройден за час, а каждый следующий на 10 минут быстрее предыдущего. Сколько часов группа затратила на весь маршрут, если последний километр спуска был пройден за 10 минут? Решение. На подъём в гору группа затратила 290 минут, на отдых 10 минут, на спуск с горы 210 минут. В сумме туристы затратили на весь маршрут 510 минут. Переведём 510 минут в часы и получим, что за 8,5 часов туристы преодолели весь маршрут . Ответ: 8,5

Слайд 29

Спасибо за внимание!

Базовый уровень: № 20 (Задачи на
смекалку)

1. За­да­ние 20 № 506313. Каж­дую
се­кун­ду бак­те­рия де­лит­ся на две новые бак­те­рии. Из­вест­но, что весь
объём од­но­го ста­ка­на бак­те­рии за­пол­ня­ют за 1 час. За сколь­ко се­кунд
бак­те­рии за­пол­ня­ют по­ло­ви­ну ста­ка­на?

По­яс­не­ние. За­ме­тим, что каж­дую
се­кун­ду в ста­ка­не ста­но­вит­ся в два раза боль­ше бак­те­рий. То есть если
в какой-то мо­мент бак­те­ри­я­ми за­пол­не­на по­ло­ви­на ста­ка­на, то через
се­кун­ду будет за­пол­нен весь ста­кан. Таким об­ра­зом, пол­ста­ка­на будет
за­пол­не­но через 59 минут и 59 се­кунд, то есть через 3599 се­кунд.

Ответ: 3599

2. За­да­ние 20 № 510016. На
палке от­ме­че­ны по­пе­реч­ные линии крас­но­го, жёлтого и зелёного цвета.
Если рас­пи­лить палку по крас­ным ли­ни­ям, по­лу­чит­ся 15 кус­ков, если по
жёлтым — 5 кус­ков, а если по зелёным — 7 кус­ков. Сколь­ко кус­ков по­лу­чит­ся,
если рас­пи­лить палку по ли­ни­ям всех трёх цве­тов?

По­яс­не­ние. Если рас­пи­лить
палку по крас­ным ли­ни­ям, то по­лу­чит­ся 15 кус­ков, сле­до­ва­тель­но,
линий — 14. Если рас­пи­лить палку по жел­тым — 5 кус­ков, сле­до­ва­тель­но,
линий — 4. Если рас­пи­лить по зе­ле­ным — 7 кус­ков, линий — 6. Всего линий:
14+4+6=24 линии, сле­до­ва­тель­но, кус­ков будет 25. Ответ: 25

3. За­да­ние 20 № 510036. Куз­не­чик
пры­га­ет вдоль ко­ор­ди­нат­ной пря­мой в любом на­прав­ле­нии на еди­нич­ный
от­ре­зок за один пры­жок. Куз­не­чик на­чи­на­ет пры­гать из на­ча­ла ко­ор­ди­нат.
Сколь­ко су­ще­ству­ет раз­лич­ных точек на ко­ор­ди­нат­ной пря­мой, в ко­то­рых
куз­не­чик может ока­зать­ся, сде­лав ровно 11 прыж­ков?

По­яс­не­ние. За­ме­тим, что куз­не­чик
может ока­зать­ся толь­ко в точ­ках с нечётными ко­ор­ди­на­та­ми, по­сколь­ку
число прыж­ков, ко­то­рое он де­ла­ет, — нечётно. Мак­си­маль­но куз­не­чик
может ока­зать­ся в точ­ках, мо­дуль ко­то­рых не пре­вы­ша­ет один­на­дца­ти.
Таким об­ра­зом, куз­не­чик может ока­зать­ся в точ­ках: −11, −9, −7, −5, −3,
−1, 1, 3, 5, 7, 9 и 11; всего 12 точек. Ответ: 12.

4. За­да­ние 20 № 510211. Саша
при­гла­сил Петю в гости, ска­зав, что живёт в седь­мом подъ­ез­де в квар­ти­ре
№ 462, а этаж ска­зать забыл. По­дой­дя к дому, Петя об­на­ру­жил, что дом се­ми­этаж­ный.
На каком этаже живёт Саша? (На всех эта­жах число квар­тир оди­на­ко­во, но­ме­ра
квар­тир в доме на­чи­на­ют­ся с еди­ни­цы.)

По­яс­не­ние. По­сколь­ку в пер­вых
7 подъ­ез­дах не мень­ше 462 квар­тир, в каж­дом подъ­ез­де не мень­ше 462 : 7
= 66 квар­тир. Сле­до­ва­тель­но, на каж­дом из 7 эта­жей в подъ­ез­де не мень­ше
9 квар­тир.

Пусть на каж­дой лест­нич­ной пло­щад­ке по 9 квар­тир.
Тогда в пер­вых семи подъ­ез­дах всего 9 · 7 · 7 = 441 квар­ти­ра, и квар­ти­ра
462 ока­жет­ся в вось­мом подъ­ез­де, что про­ти­во­ре­чит усло­вию.

Пусть на каж­дой пло­щад­ке по 10 квар­тир. Тогда в
пер­вых семи подъ­ез­дах 10 · 7 · 7 = 490 квар­тир, а в пер­вых шести — 420.
Сле­до­ва­тель­но, квар­ти­ра 462 на­хо­дит­ся в седь­мом подъ­ез­де. Она в нем
42-ая по счету, по­сколь­ку на этаже по 10 квар­тир, она рас­по­ло­же­на на
пятом этаже.

Если бы на каж­дой пло­щад­ке было по 11 квар­тир, то
в пер­вых шести подъ­ез­дах ока­за­лось бы 11 · 7 · 6 = 462 квар­ти­ры, то есть
462 квар­ти­ра в ше­стом подъ­ез­де, что про­ти­во­ре­чит усло­вию.

Т.о., Саша живёт на пятом этаже. Ответ: 5

5. За­да­ние 20 № 510231. Саша
при­гла­сил Петю в гости, ска­зав, что живёт в вось­мом подъ­ез­де в квар­ти­ре
№ 468, а этаж ска­зать забыл. По­дой­дя к дому, Петя об­на­ру­жил, что дом две­на­дца­ти­этаж­ный.
На каком этаже живёт Саша? (На всех эта­жах число квар­тир оди­на­ко­во, но­ме­ра
квар­тир в доме на­чи­на­ют­ся с еди­ни­цы.)

По­яс­не­ние. По­сколь­ку в пер­вых
8 подъ­ез­дах не мень­ше 468 квар­тир, в каж­дом подъ­ез­де не мень­ше 468 : 8
= 58,5 квар­тир. Сле­до­ва­тель­но, на каж­дом из 12 эта­жей в подъ­ез­де не
мень­ше 4 квар­тир.

Пусть на каж­дой лест­нич­ной пло­щад­ке по 4 квар­ти­ры.
Тогда в пер­вых вось­ми подъ­ез­дах всего 4 · 8 · 12 = 384 квар­ти­ры, и квар­ти­ра
468 ока­жет­ся не в вось­мом подъ­ез­де, что про­ти­во­ре­чит усло­вию.

Пусть на каж­дой пло­щад­ке по 5 квар­тир. Тогда в пер­вых
вось­ми подъ­ез­дах 5 · 8 · 12 = 480 квар­тир, а в пер­вых семи — 420. Сле­до­ва­тель­но,
квар­ти­ра 468 на­хо­дит­ся в вось­мом подъ­ез­де. Она в нем 48-ая по счету, по­сколь­ку
на этаже по 5 квар­тир, она рас­по­ло­же­на на де­ся­том этаже.

Если бы на каж­дой пло­щад­ке было по 6 квар­тир, то в
пер­вых семи подъ­ез­дах ока­за­лось бы 6 · 7 · 12 = 504 квар­ти­ры, то есть
482 квар­ти­ра в седь­мом подъ­ез­де, что про­ти­во­ре­чит усло­вию.

Т.о., Саша живёт на де­ся­том этаже.  Ответ: 10

6. За­да­ние 20 № 510251. Саша
при­гла­сил Петю в гости, ска­зав, что живёт в две­на­дца­том подъ­ез­де в квар­ти­ре
№ 465, а этаж ска­зать забыл. По­дой­дя к дому, Петя об­на­ру­жил, что дом пя­ти­этаж­ный.
На каком этаже живёт Саша? (На всех эта­жах число квар­тир оди­на­ко­во, но­ме­ра
квар­тир в доме на­чи­на­ют­ся с еди­ни­цы.)

По­яс­не­ние. По­сколь­ку в пер­вых
12 подъ­ез­дах не мень­ше 465 квар­тир, в каж­дом подъ­ез­де не мень­ше 465 :
12 = 38,75 квар­тир. Сле­до­ва­тель­но, на каж­дом из 5 эта­жей в подъ­ез­де не
мень­ше 7 квар­тир.

Пусть на каж­дой лест­нич­ной пло­щад­ке по 7 квар­тир.
Тогда в пер­вых две­на­дца­ти подъ­ез­дах всего       12 · 7 · 5 = 420 квар­ти­р,
и квар­ти­ра 465 ока­жет­ся в три­на­дца­том подъ­ез­де, что про­ти­во­ре­чит
усло­вию.

Пусть на каж­дой пло­щад­ке по 8 квар­тир. Тогда в пер­вых
две­на­дца­ти подъ­ез­дах 12 · 8 · 5 = 480 квар­тир, а в пер­вых один­на­дца­ти
— 440. Сле­до­ва­тель­но, квар­ти­ра 465 на­хо­дит­ся в две­на­дца­том подъ­ез­де.
Она в нем 25-ая по счету, по­сколь­ку на этаже по 8 квар­тир, она рас­по­ло­же­на
на чет­вер­том этаже.

Т.о., Саша живёт на чет­вер­том этаже.  Ответ: 4

7. За­да­ние 20 № 510271. Саша
при­гла­сил Петю в гости, ска­зав, что живёт в де­ся­том подъ­ез­де в квар­ти­ре
№ 333, а этаж ска­зать забыл. По­дой­дя к дому, Петя об­на­ру­жил, что дом де­вя­ти­этаж­ный.
На каком этаже живёт Саша? (На всех эта­жах число квар­тир оди­на­ко­во, но­ме­ра
квар­тир в доме на­чи­на­ют­ся с еди­ни­цы.)

По­яс­не­ние. По­сколь­ку в пер­вых
10 подъ­ез­дах не мень­ше 333 квар­тир, в каж­дом подъ­ез­де не мень­ше 333 :
10 = 33,3 квар­тир. Сле­до­ва­тель­но, на каж­дом из 9 эта­жей в подъ­ез­де не
мень­ше 3 квар­тир.

Пусть на каж­дой лест­нич­ной пло­щад­ке по 3 квар­тиры.
Тогда в пер­вых де­ся­ти подъ­ез­дах всего 10 · 3· 9 = 270 квар­ти­ра, и квар­ти­ра
333 ока­жет­ся в один­на­дца­том подъ­ез­де, что про­ти­во­ре­чит усло­вию.

Пусть на каж­дой пло­щад­ке по 4 квар­тиры. Тогда в
пер­вых де­ся­ти подъ­ез­дах 10 · 4 · 9 = 360 квар­тир, а в пер­вых де­вя­ти —
324. Сле­до­ва­тель­но, квар­ти­ра 333 на­хо­дит­ся в де­ся­том подъ­ез­де. Она
в нем 9-ая по счету, по­сколь­ку на этаже по 4 квар­тиры, она рас­по­ло­же­на
на тре­тьем этаже.

Т.о., Саша живёт на тре­тьем этаже. Ответ: 3

8. За­да­ние 20 № 507073. Тре­нер
по­со­ве­то­вал Ан­дрею в пер­вый день за­ня­тий про­ве­сти на бе­го­вой до­рож­ке
15 минут, а на каж­дом сле­ду­ю­щем за­ня­тии уве­ли­чи­вать время, про­ведённое
на бе­го­вой до­рож­ке, на 7 минут. За сколь­ко за­ня­тий Ан­дрей про­ведёт на
бе­го­вой до­рож­ке в общей слож­но­сти 2 часа 25 минут, если будет сле­до­вать
со­ве­там тре­не­ра?

По­яс­не­ние. Время, про­ведённое
на бе­го­вой до­рож­ке пред­став­ля­ет собой ариф­ме­ти­че­скую про­грес­сию с
пер­вым чле­ном рав­ным 15 и раз­но­стью 7. Сумма  чле­нов
ариф­ме­ти­че­ской про­грес­сии может быть най­де­на по фор­му­ле:  По­лу­чи­ли
квад­рат­ное урав­не­ние на  решим
его:  По усло­вию за­да­чи под­хо­дит
зна­че­ние      Ответ: 5.

9. За­да­ние 20 № 507074. Врач
про­пи­сал па­ци­ен­ту при­ни­мать ле­кар­ство по такой схеме: в пер­вый день
он дол­жен при­нять 3 капли, а в каж­дый сле­ду­ю­щий день — на 3 капли боль­ше,
чем в преды­ду­щий. При­няв 30 ка­пель, он ещё 3 дня пьёт по 30 ка­пель ле­кар­ства,
а потом еже­днев­но умень­ша­ет приём на 3 капли. Сколь­ко пу­зырь­ков ле­кар­ства
нужно ку­пить па­ци­ен­ту на весь курс приёма, если в каж­дом со­дер­жит­ся 20
мл ле­кар­ства (что со­став­ля­ет 250 ка­пель)?

По­яс­не­ние. На пер­вом этапе
приёма ка­пель число при­ни­ма­е­мых ка­пель в день пред­став­ля­ет собой воз­рас­та­ю­щую
ариф­ме­ти­че­скую про­грес­сию с пер­вым чле­ном, рав­ным 3, раз­но­стью, рав­ной
3 и по­след­ним чле­ном, рав­ным 30. Сле­до­ва­тель­но,

этап,
когда число ка­пель в день воз­рас­та­ет про­дол­жа­ет­ся  Сум­мар­ное
число ка­пель, при­ня­тых в этот пе­ри­од, пред­став­ля­ет собой сумму ариф­ме­ти­че­ской
про­грес­сии: 

Затем в те­че­ние трёх дней па­ци­ент при­ни­ма­ет ещё  По­след­ний
этап приёма ка­пель длит­ся  Ана­ло­гич­но
пер­во­му этапу: 

Таким об­ра­зом, за весь курс приёма па­ци­ен­ту нужно
при­нять 165 + 90 + 135 = 390 ка­пель. То есть нужно при­об­ре­сти не мень­ше  пу­зырь­ков
ле­кар­ства.    Ответ: 2.

 10. За­да­ние 20 № 509705. Врач
про­пи­сал па­ци­ен­ту при­ни­мать ле­кар­ство по такой схеме: в пер­вый день
он дол­жен при­нять 20 ка­пель, а в каж­дый сле­ду­ю­щий день — на 3 капли боль­ше,
чем в преды­ду­щий. После 15 дней приёма па­ци­ент де­ла­ет пе­ре­рыв в 3 дня и
про­дол­жа­ет при­ни­мать ле­кар­ство по об­рат­ной схеме: в 19-й день он при­ни­ма­ет
столь­ко же ка­пель, сколь­ко и в 15-й день, а затем еже­днев­но умень­ша­ет
дозу на 3 капли, пока до­зи­ров­ка не ста­нет мень­ше 3 ка­пель в день. Сколь­ко
пу­зырь­ков ле­кар­ства нужно ку­пить па­ци­ен­ту на весь курс приёма, если в
каж­дом со­дер­жит­ся 200 ка­пель?

По­яс­не­ние. С на­ча­ла курса
до 15 дня приёма ле­кар­ства (вклю­чи­тель­но), па­ци­ент будет при­ни­мать каж­дый
день на три капли боль­ше, чем в преды­ду­щий, сле­до­ва­тель­но, к 15 дню
приёма ле­кар­ства па­ци­ент при­мет 600 ка­пель. С 19 дня до конца приёма ле­кар­ства
он вы­пьет столь­ко же, но на 80 ка­пель боль­ше. Сле­до­ва­тель­но, за весь
курс приёма ле­кар­ства па­ци­ент вы­пьет
600 + 600 + 80 = 1280 ка­пель ле­кар­ства. Те­перь
найдём сколь­ко пу­зырь­ков нужно ку­пить:
1280 : 200 = 6,4.    Ответ:
7

11. За­да­ние 20 № 507075. Про­из­ве­де­ние
де­ся­ти иду­щих под­ряд чисел раз­де­ли­ли на 7. Чему может быть равен оста­ток?

По­яс­не­ние. Среди 10 под­ряд
иду­щих чисел одно из них обя­за­тель­но будет де­лить­ся на 7, по­это­му про­из­ве­де­ние
этих чисел крат­но семи. Сле­до­ва­тель­но, оста­ток от де­ле­ния на 7 равен
нулю.  Ответ: 0.

12. За­да­ние 20 № 507076. Сколь­ки­ми
спо­со­ба­ми можно по­ста­вить в ряд два оди­на­ко­вых крас­ных ку­би­ка, три
оди­на­ко­вых зелёных ку­би­ка и один синий кубик?

По­яс­не­ние. За­ну­ме­ру­ем все
ку­би­ки от од­но­го до шести. Пока не учи­ты­ва­ем, что в нашем на­бо­ре есть
ку­би­ки оди­на­ко­во­го цвета. На пер­вое место можно по­ста­вить кубик ше­стью
спо­со­ба­ми, на вто­рое — пятью, на тре­тье — че­тырь­мя и так далее. По­лу­ча­ем,
что всего воз­мож­но­стей рас­ста­нов­ки ку­би­ков  Те­перь
учтём, что пе­ре­ста­нов­ка, на­при­мер, двух крас­ных ку­би­ков не даёт но­во­го
спо­со­ба рас­ста­нов­ки ку­би­ков. В любом по­лу­чен­ном выше на­бо­ре можно
пе­ре­ста­вить крас­ные ку­би­ки ме­ста­ми, то есть число рас­ста­но­вок умень­шит­ся
в два раза. С зелёными ку­би­ка­ми ана­ло­гич­но. Зелёных ку­би­ков три, по­это­му
в любом по­лу­чен­ном выше на­бо­ре можно пе­ре­став­лять их, не по­лу­чая
новых спо­со­бов рас­ста­нов­ки ку­би­ков. Таких пе­ре­ста­но­вок зелёных ку­би­ков 

Сле­до­ва­тель­но, ис­ко­мое число спо­со­бов равно:             
Ответ: 60.

13. За­да­ние 20 № 507077. В
бак объёмом 38 лит­ров каж­дый час, на­чи­ная с 12 часов, на­ли­ва­ют пол­ное
ведро воды объёмом 8 лит­ров. Но в днище бака есть не­боль­шая щель, и из неё
за час вы­те­ка­ет 3 литра. В какой мо­мент вре­ме­ни (в часах) бак будет за­пол­нен
пол­но­стью.

По­яс­не­ние. К концу каж­до­го
часа объём воды в баке уве­ли­чи­ва­ет­ся на 8 − 3 = 5 лит­ров. Через 6 часов,
то есть в 18 часов, в баке будет 30 лит­ров воды. В 18 часов в бак до­льют 8
лит­ров воды и объём воды в баке ста­нет рав­ным 38 лит­ров. Ответ: 18.

14. За­да­ние 20 № 507078. Какое
наи­мень­шее число иду­щих под­ряд чисел нужно взять, чтобы их про­из­ве­де­ние
де­ли­лось на 7?

По­яс­не­ние. До­ста­точ­но
взять два числа, одно из ко­то­рых крат­но семи, на­при­мер, 7 и 8. Ответ: 2.

При­ме­ча­ние.
Если
бы усло­вие за­да­чи зву­ча­ло так: «Какое наи­мень­шее число иду­щих под­ряд
чисел нужно взять, чтобы их про­из­ве­де­ние га­ран­ти­ро­ва­но де­ли­лось
на 7?» То нужно было бы взять семь под­ряд иду­щих чисел.  

15. За­да­ние 20 № 507079. В ре­зуль­та­те
па­вод­ка кот­ло­ван за­пол­нил­ся водой до уров­ня 2 метра. Стро­и­тель­ная
помпа не­пре­рыв­но от­ка­чи­ва­ет воду, по­ни­жая её уро­вень на 20 см в час.
Под­поч­вен­ные воды, на­о­бо­рот, по­вы­ша­ют уро­вень воды в кот­ло­ва­не на
5 см в час. За сколь­ко часов ра­бо­ты помпы уро­вень воды в кот­ло­ва­не опу­стит­ся
до 80 см?

По­яс­не­ние. За час уро­вень
воды в кот­ло­ва­не умень­ша­ет­ся на 20 − 5 = 15 см. Нужно от­ка­чать
2 · 100 − 80 = 120 см воды. Сле­до­ва­тель­но, уро­вень воды в кот­ло­ва­не
опу­стит­ся до 80 см за    Ответ: 8.

16. За­да­ние 20 № 507080. В
меню ре­сто­ра­на име­ет­ся 6 видов са­ла­тов, 3 вида пер­вых блюд, 5 видов вто­рых
блюд и 4 вида де­сер­та. Сколь­ко ва­ри­ан­тов обеда из са­ла­та, пер­во­го,
вто­ро­го и де­сер­та могут вы­брать по­се­ти­те­ли этого ре­сто­ра­на?

По­яс­не­ние. Салат можно вы­брать
ше­стью спо­со­ба­ми, пер­вое — тремя, вто­рое — пятью, де­серт — че­тырь­мя.
Сле­до­ва­тель­но, всего
6 · 3 · 5 · 4 = 360 ва­ри­ан­тов обеда.  
Ответ: 360.

17. За­да­ние 20 № 507081. Неф­тя­ная
ком­па­ния бурит сква­жи­ну для до­бы­чи нефти, ко­то­рая за­ле­га­ет, по дан­ным
гео­ло­го­раз­вед­ки, на глу­би­не 3 км. В те­че­ние ра­бо­че­го дня бу­риль­щи­ки
про­хо­дят 300 мет­ров в глу­би­ну, но за ночь сква­жи­на вновь «за­или­ва­ет­ся»,
то есть за­пол­ня­ет­ся грун­том на 30 мет­ров. За сколь­ко ра­бо­чих дней неф­тя­ни­ки
про­бу­рят сква­жи­ну до глу­би­ны за­ле­га­ния нефти?

По­яс­не­ние. За день сква­жи­на
уве­ли­чи­ва­ет­ся на 300 − 30 = 270 м. к на­ча­лу один­на­дца­то­го ра­бо­че­го
дня неф­тя­ни­ки про­бу­рят 2700 мет­ров. За один­на­дца­тый ра­бо­чий день неф­тя­ни­ки
про­бу­рят ещё 300 мет­ров, то есть дой­дут до глу­би­ны 3 км.   Ответ: 11.

При­ме­ча­ние.
В
дей­стви­тель­но­сти, часто, на на­сто­я­щих бу­ро­вых выш­ках, неф­тя­ни­ки
бурят в три смены, по­это­му у них сква­жи­ны за­или­вать­ся не успе­ва­ют.

18. За­да­ние 20 № 507083. Какое
наи­мень­шее число иду­щих под­ряд чисел нужно взять, чтобы их про­из­ве­де­ние
де­ли­лось на 9?

По­яс­не­ние. До­ста­точ­но
взять два числа, одно из ко­то­рых крат­но де­вя­ти, на­при­мер, 9 и 10. Ответ: 2.

При­ме­ча­ние.
Если
бы усло­вие за­да­чи зву­ча­ло так: «Какое наи­мень­шее число иду­щих под­ряд
чисел нужно взять, чтобы их про­из­ве­де­ние га­ран­ти­ро­ва­но де­ли­лось
на 9?» То нужно было бы взять шесть под­ряд иду­щих чисел.

19. За­да­ние 20 № 509227. В об­мен­ном
пунк­те можно со­вер­шить одну из двух опе­ра­ций:

• за 2 зо­ло­тых мо­не­ты по­лу­чить 3 се­реб­ря­ных и
одну мед­ную;

• за 5 се­реб­ря­ных монет по­лу­чить 3 зо­ло­тых и
одну мед­ную.

У Ни­ко­лая были толь­ко се­реб­ря­ные мо­не­ты. После
не­сколь­ких по­се­ще­ний об­мен­но­го пунк­та се­реб­ря­ных монет у него стало
мень­ше, зо­ло­тых не по­яви­лось, зато по­яви­лось 50 мед­ных. На сколь­ко
умень­ши­лось ко­ли­че­ство се­реб­ря­ных монет у Ни­ко­лая?

По­яс­не­ние. Пусть Ни­ко­лай
сде­лал сна­ча­ла  опе­ра­ций
вто­ро­го типа, а затем  опе­ра­ций
пер­во­го типа.

Тогда имеем: 

Тогда се­реб­ря­ных монет стало на  боль­ше,
то есть на 10 мень­ше. Ответ: 10

20. За­да­ние 20 № 509625. На
по­верх­но­сти гло­бу­са фло­ма­сте­ром про­ве­де­ны 12 па­рал­ле­лей и 22 ме­ри­ди­а­на.
На сколь­ко ча­стей про­ведённые линии раз­де­ли­ли по­верх­ность гло­бу­са?

Ме­ри­ди­ан — это дуга окруж­но­сти, со­еди­ня­ю­щая
Се­вер­ный и Южный по­лю­сы. Па­рал­лель — это окруж­ность, ле­жа­щая в плос­ко­сти,
па­рал­лель­ной плос­ко­сти эк­ва­то­ра.

По­яс­не­ние. Две­на­дцать па­рал­ле­лей
раз­де­ли­ли гло­бус на 13 ча­стей, сле­до­ва­тель­но
13 · 22 = 286 — на столь­ко ча­стей раз­де­лят гло­бус 12
па­рал­ле­лей и 22 ме­ри­ди­а­ны. Ответ:
286

21. За­да­ние 20 № 509665. В
кор­зи­не лежит 50 гри­бов: ры­жи­ки и груз­ди. Из­вест­но, что среди любых 28
гри­бов име­ет­ся хотя бы один рыжик, а среди любых 24 гри­бов хотя бы один
груздь. Сколь­ко груз­дей в кор­зи­не?

По­яс­не­ние. В кор­зи­не точно
лежит 27 груз­дей и 23 ры­жи­ка, так как взять 28 груз­дей, как и 24 ры­жи­ка,
не по­лу­чит­ся.  Ответ: 27

22. За­да­ние 20 № 509725. Груп­па
ту­ри­стов пре­одо­ле­ла гор­ный пе­ре­вал. Пер­вый ки­ло­метр подъёма они пре­одо­ле­ли
за 50 минут, а каж­дый сле­ду­ю­щий ки­ло­метр про­хо­ди­ли на 15 минут доль­ше
преды­ду­ще­го. По­след­ний ки­ло­метр перед вер­ши­ной был прой­ден за 95
минут. После де­ся­ти­ми­нут­но­го от­ды­ха на вер­ши­не ту­ри­сты на­ча­ли
спуск, ко­то­рый был более по­ло­гим. Пер­вый ки­ло­метр после вер­ши­ны был
прой­ден за час, а каж­дый сле­ду­ю­щий на 10 минут быст­рее преды­ду­ще­го.
Сколь­ко часов груп­па за­тра­ти­ла на весь марш­рут, если по­след­ний ки­ло­метр
спус­ка был прой­ден за 10 минут.

По­яс­не­ние. На подъём в гору
груп­па за­тра­ти­ла 290 минут, на отдых 10 минут, на спуск с горы 210 минут. В
сумме ту­ри­сты за­тра­ти­ли на весь марш­рут 510 минут. Пе­ре­ведём 510 минут
в часы и по­лу­чим, что за 8,5 часов ту­ри­сты пре­одо­ле­ли весь марш­рут. Ответ: 8,5

23. За­да­ние 20 № 509986. На
коль­це­вой до­ро­ге рас­по­ло­же­ны че­ты­ре бен­зо­ко­лон­ки: A, B, C и D.
Рас­сто­я­ние между A и B — 35 км, между A и C — 20 км,
между C и D — 20 км, между D и A — 30 км (все рас­сто­я­ния из­ме­ря­ют­ся
вдоль коль­це­вой до­ро­ги в крат­чай­шую сто­ро­ну). Най­ди­те рас­сто­я­ние
между B и C. Ответ дайте в ки­ло­мет­рах.

По­яс­не­ние.

Рас­по­ло­жим А,
В, C, D вдоль коль­це­вой до­ро­ги по оче­ре­ди так, чтобы рас­сто­я­ния со­от­вет­ство­ва­ли
дан­ным в усло­вии. Всё хо­ро­шо, кроме рас­сто­я­ния между D и A. Чтобы оно
было таким, каким нужно, по­дви­нем D и по­ста­вим между B и A нуж­ным об­ра­зом.
Тогда между B и C будет 15 км.

Ответ: 15.

24. За­да­ние 20 № 506383. На
коль­це­вой до­ро­ге рас­по­ло­же­ны че­ты­ре бен­зо­ко­лон­ки: A, B, C и D.
Рас­сто­я­ние между A и B — 50 км, между A и C — 40 км, между C и D — 25
км, между D и A — 35 км (все рас­сто­я­ния из­ме­ря­ют­ся вдоль коль­це­вой до­ро­ги
в крат­чай­шую сто­ро­ну). Най­ди­те рас­сто­я­ние между B и C.

По­яс­не­ние.

Рас­по­ло­жим А,
В, C, D вдоль коль­це­вой до­ро­ги по оче­ре­ди так, чтобы рас­сто­я­ния со­от­вет­ство­ва­ли
дан­ным в усло­вии. Всё хо­ро­шо, кроме рас­сто­я­ния между D и A. Чтобы оно
было таким, каким нужно, по­дви­нем D и по­ста­вим между B и A нуж­ным об­ра­зом.
Тогда между B и D будет 15 км. А между B и С —10 км.

Ответ: 10

25. За­да­ние 20 № 506319. В
клас­се учит­ся 25 уча­щих­ся. Не­сколь­ко из них хо­ди­ли в кино, 18 че­ло­век
хо­ди­ли в театр, причём и в кино, и в театр хо­ди­ли 12 че­ло­век. Из­вест­но,
что трое не хо­ди­ли ни в кино, ни в театр. Сколь­ко че­ло­век из клас­са хо­ди­ли
в кино?

По­яс­не­ние. 12 че­ло­век хо­ди­ли
и в кино, и в театр. А всего в театр хо­ди­ло 18 че­ло­век. Зна­чит, 6 че­ло­век
хо­ди­ли толь­ко в театр.

Схо­ди­ли в театр или в кино и в театр, или ни­ку­да
не хо­ди­ли —  че­ло­век.
Зна­чит,  че­ло­ве­ка
хо­ди­ли толь­ко в кино. И зна­чит всего в кино схо­ди­ло  че­ло­век.

   Ответ: 16

26. За­да­ние 20 № 506733. По
эм­пи­ри­че­ско­му за­ко­ну Мура сред­нее число тран­зи­сто­ров на мик­ро­схе­мах
каж­дый год удва­и­ва­ет­ся. Из­вест­но, что в 2005 году сред­нее число тран­зи­сто­ров
на мик­ро­схе­ме рав­ня­лось 520 млн. Опре­де­ли­те, сколь­ко в сред­нем
мил­ли­о­нов тран­зи­сто­ров было на мик­ро­схе­ме в 2003 году.

По­яс­не­ние.  Каж­дый год число
тран­зи­сто­ров удва­и­ва­ет­ся, по­это­му в 2004 году сред­нее число тран­зи­сто­ров
рав­ня­лось 520/2 = 260 млн, а в 2003 —
260/2 = 130 млн.   Ответ: 130.

27. За­да­ние 20 № 506732. В
пер­вом ряду ки­но­за­ла 24 места, а в каж­дом сле­ду­ю­щем на 2 боль­ше, чем в
преды­ду­щем. Сколь­ко мест в вось­мом ряду?

По­яс­не­ние. Число мест в ряду
пред­став­ля­ет собой ариф­ме­ти­че­скую про­грес­сию с пер­вым чле­ном  и
раз­но­стью  Член
ариф­ме­ти­че­ской про­грес­сии с но­ме­ром  может
быть най­ден по фор­му­ле    Не­об­хо­ди­мо
найти ,
имеем:      Ответ: 38.

28. За­да­ние 20 № 506443. На
палке от­ме­че­ны по­пе­реч­ные линии крас­но­го, жёлтого и зелёного цвета.
Если рас­пи­лить палку по крас­ным ли­ни­ям, по­лу­чит­ся 5 кус­ков, если по
жёлтым — 7 кус­ков, а если по зелёным — 11 кус­ков. Сколь­ко кус­ков по­лу­чит­ся,
если рас­пи­лить палку по ли­ни­ям всех трёх цве­тов?

По­яс­не­ние. Каж­дый рас­пил
уве­ли­чи­ва­ет ко­ли­че­ство кус­ков на один. То есть всего 4 крас­ные линии,
6 жёлтых и 10 зелёных. То есть вме­сте 20 линий. А кус­ков по­лу­чит­ся 21. Ответ: 21

29. За­да­ние 20 № 506343. В ма­га­зи­не
бы­то­вой тех­ни­ки объём про­даж хо­ло­диль­ни­ков носит се­зон­ный ха­рак­тер.
В ян­ва­ре было про­да­но 10 хо­ло­диль­ни­ков, и в три по­сле­ду­ю­щих ме­ся­ца
про­да­ва­ли по 10 хо­ло­диль­ни­ков. С мая про­да­жи уве­ли­чи­ва­лись на 15
еди­ниц по срав­не­нию с преды­ду­щим ме­ся­цем. С сен­тяб­ря объём про­даж
начал умень­шать­ся на 15 хо­ло­диль­ни­ков каж­дый месяц от­но­си­тель­но
преды­ду­ще­го ме­ся­ца. Сколь­ко хо­ло­диль­ни­ков про­дал ма­га­зин за год?

По­яс­не­ние.
По­сле­до­ва­тель­но
рас­счи­та­ем сколь­ко хо­ло­диль­ни­ков было про­да­но за каж­дый месяц и про­сум­ми­ру­ем
ре­зуль­та­ты:

        Ответ: 360.

30. За­да­ние 20 № 506423. В об­мен­ном
пунк­те можно со­вер­шить одну из двух опе­ра­ций:

·    за 3 зо­ло­тых
мо­не­ты по­лу­чить 4 се­реб­ря­ных и одну мед­ную;

·    за 6 се­реб­ря­ных
монет по­лу­чить 4 зо­ло­тых и одну мед­ную.

У Ни­ко­лы были толь­ко се­реб­ря­ные мо­не­ты. После
по­се­ще­ний об­мен­но­го пунк­та се­реб­ря­ных монет у него стало мень­ше, зо­ло­тых
не по­яви­лось, зато по­яви­лось 35 мед­ных. На сколь­ко умень­ши­лось ко­ли­че­ство
се­реб­ря­ных монет у Ни­ко­лы?

По­яс­не­ние. Пусть Ни­ко­ла сде­лал
сна­ча­ла  опе­ра­ций
вто­ро­го типа, а затем  опе­ра­ций
пер­во­го типа. Тогда имеем:

Тогда се­реб­ря­ных монет стало на  боль­ше,
то есть на 10 мень­ше. Ответ: 10

31. За­да­ние 20 № 506403. Саша
при­гла­сил Петю в гости, ска­зав, что живёт в седь­мом подъ­ез­де в квар­ти­ре
№ 462, а этаж ска­зать забыл. По­дой­дя к дому, Петя об­на­ру­жил, что дом
се­ми­этаж­ный. На каком этаже живёт Саша? (На каж­дом этаже число квар­тир оди­на­ко­во,
но­ме­ра квар­тир в доме на­чи­на­ют­ся с еди­ни­цы.)

По­яс­не­ние. По­сколь­ку в пер­вых
7 подъ­ез­дах не мень­ше 462 квар­тир, в каж­дом подъ­ез­де не мень­ше
462 : 7 =  66 квар­тир. Сле­до­ва­тель­но, на каж­дом из 7
этаже в подъ­ез­де не мень­ше 9 квар­тир.

Пусть на каж­дой лест­нич­ной пло­щад­ке по 9 квар­тир.
Тогда в пер­вых семи подъ­ез­дах всего 9 · 7 · 7 = 441 квар­ти­ра,
и квар­ти­ра 462 ока­жет­ся в вось­мом подъ­ез­де, что про­ти­во­ре­чит усло­вию.

Пусть на каж­дой пло­щад­ке по 10 квар­тир. Тогда в
пер­вых семи подъ­ез­дах 10 · 7 · 7 = 490 квар­тир, а в пер­вых
шести — 420. Сле­до­ва­тель­но, квар­ти­ра 462 на­хо­дит­ся в седь­мом
подъ­ез­де. Она в нем 42-ая по счету, по­сколь­ку на этаже по 10 квар­тир, она
рас­по­ло­же­на на пятом этаже.

Если бы на каж­дой пло­щад­ке было по 11 квар­тир, то
в пер­вых шести подъ­ез­дах ока­за­лось бы
11 · 7 · 6 = 462 квар­ти­ры, то есть 462 квар­ти­ра
в ше­стом подъ­ез­де, что про­ти­во­ре­чит усло­вию.

Т.о., Саша живёт на пятом этаже. Ответ: 5.

32. За­да­ние 20 № 506730. Во всех
подъ­ез­дах дома оди­на­ко­вое число эта­жей, а на каж­дом этаже оди­на­ко­вое
число квар­тир. При этом число эта­жей в доме боль­ше числа квар­тир на этаже,
число квар­тир на этаже боль­ше числа подъ­ез­дов, а число подъ­ез­дов боль­ше
од­но­го. Сколь­ко эта­жей в доме, если всего в нём 110 квар­тир?

По­яс­не­ние. Число квар­тир,
эта­жей и подъ­ез­дов может быть толь­ко целым чис­лом. За­ме­тим, что число
110 де­лит­ся на 2, 5 и 11. Сле­до­ва­тель­но, в доме долж­но быть 2 подъ­ез­да,
5 квар­тир и 11 эта­жей. Ответ: 11

33. За­да­ние 20 № 506731. Куз­не­чик
пры­га­ет вдоль ко­ор­ди­нат­ной пря­мой в любом на­прав­ле­нии на еди­нич­ный
от­ре­зок за пры­жок. Сколь­ко су­ще­ству­ет раз­лич­ных точек на ко­ор­ди­нат­ной
пря­мой, в ко­то­рых куз­не­чик может ока­зать­ся, сде­лав ровно 6 прыж­ков, на­чи­ная
пры­гать из на­ча­ла ко­ор­ди­нат?

По­яс­не­ние. За­ме­тим, что куз­не­чик
может ока­зать­ся толь­ко в точ­ках с чётными ко­ор­ди­на­та­ми, по­сколь­ку
число прыж­ков, ко­то­рое он де­ла­ет, — чётно. Мак­си­маль­но куз­не­чик может
ока­зать­ся в точ­ках, мо­дуль ко­то­рых не пре­вы­ша­ет шести. Таким об­ра­зом,
куз­не­чик может ока­зать­ся в точ­ках: −6, −4, −2, 0, 2, 4 и 6; всего 7 точек.  
Ответ: 7.

34. За­да­ние 20 № 506646. В
кор­зи­не лежат 40 гри­бов: ры­жи­ки и груз­ди. Из­вест­но, что среди любых 17
гри­бов име­ет­ся хотя бы один рыжик, а среди любых 25 гри­бов хотя бы один
груздь. Сколь­ко ры­жи­ков в кор­зи­не?

По­яс­не­ние. В кор­зи­не име­ет­ся
как ми­ни­мум 24 ры­жи­ка. Иначе мы бы могли взять 17 груз­дей, и пер­вое усло­вие
бы не вы­пол­ни­лось. Ана­ло­гич­но из вто­ро­го усло­вия вы­те­ка­ет, что в
кор­зи­не как ми­ни­мум 16 груз­дей. Из этих двух утвер­жде­ний можно сде­лать
вывод, что в кор­зи­не ровно 24 ры­жи­ка и 16 груз­дей.

 ———- 
Дуб­ли­ру­ет за­да­ние 506363.   Ответ:
24

35. За­да­ние 20 № 506363. В
кор­зи­не лежат 25 гри­бов: ры­жи­ки и груз­ди. Из­вест­но, что среди любых 11
гри­бов име­ет­ся хотя бы один рыжик, а среди любых 16 гри­бов хотя бы один
груздь. Сколь­ко ры­жи­ков в кор­зи­не?

По­яс­не­ние. Пусть мы взяли 10
груз­дей. Тогда все осталь­ные грибы — ры­жи­ки, иначе бы мы взяли груздь и
усло­вие бы на­ру­ши­лось. Таким об­ра­зом, в кор­зи­не ми­ни­мум 15 ры­жи­ков.
Те­перь возьмём 15 ры­жи­ков. Тогда все осталь­ные груз­ди, иначе ана­ло­гич­но
пер­во­му слу­чаю мы бы взяли один из остав­ших­ся ры­жи­ков, и усло­вие бы не
вы­пол­ни­лось. От­сю­да сле­ду­ет, что в кор­зи­не ми­ни­мум 10 груз­дей. Ми­ни­мум
15 ры­жи­ков и ми­ни­мум 10 груз­дей. А всего гри­бов 25. Зна­чит, среди них
имен­но 15 ры­жи­ков и 10 груз­дей.

Ответ: 15

36. За­да­ние 20 № 506835. В
кор­зи­не лежат 30 гри­бов: ры­жи­ки и груз­ди. Из­вест­но, что среди любых 12
гри­бов име­ет­ся хотя бы один рыжик, а среди любых 20 гри­бов хотя бы один груздь.
Сколь­ко ры­жи­ков в кор­зи­не?

По­яс­не­ние. В кор­зи­не есть
как ми­ни­мум 19 ры­жи­ков. Иначе можно было бы взять 12 груз­дей и пер­вое
усло­вие не вы­пол­ня­лось. Ана­ло­гич­но из вто­ро­го усло­вия сле­ду­ет, что
в кор­зи­не как ми­ни­мум 11 груз­дей. Со­по­став­ляя эти два факта, по­лу­чим,
что в кор­зи­не имен­но 19 ры­жи­ков и 11 груз­дей. Ответ: 19.

 ———- 
Дуб­ли­ру­ет за­да­ние 506363.  Ответ:
19

37. За­да­ние 20 № 506729. На
гло­бу­се фло­ма­сте­ром про­ве­де­ны 17 па­рал­ле­лей (вклю­чая эк­ва­тор) и
24 ме­ри­ди­а­на. На сколь­ко ча­стей про­ведённые линии раз­де­ля­ют по­верх­ность
гло­бу­са?

По­яс­не­ние. Пред­ста­вим, что
на гло­бу­се ещё не на­ри­со­ва­ны па­рал­ле­ли и ме­ри­ди­а­ны. За­ме­тим, что
24 ме­ри­ди­а­на раз­де­лят гло­бус на 24 части. Рас­смот­рим сек­тор, об­ра­зо­ван­ный
двумя со­сед­ни­ми ме­ри­ди­а­на­ми. Про­ве­де­ние пер­вой па­рал­ле­ли раз­де­лит
сек­тор на две части, про­ве­де­ние вто­рой до­ба­вить ещё одну часть, и так
далее, таким об­ра­зом, 17 па­рал­ле­лей раз­де­лят сек­тор на 18 ча­стей. Сле­до­ва­тель­но,
весь гло­бус будет раз­бит на 24 · 18 = 432 части.  Ответ: 432.

38. За­да­ние 20 № 506523. Улит­ка
за день за­пол­за­ет вверх по де­ре­ву на 4 м, а за ночь спол­за­ет на 3 м. Вы­со­та
де­ре­ва 10 м. За сколь­ко дней улит­ка впер­вые до­ползёт до вер­ши­ны де­ре­ва?

По­яс­не­ние. За день улит­ка за­ползёт
на 4 метра, а за ночь — сползёт на 3 метра. Итого за сутки она за­ползёт на
метр. За ше­сте­ро суток она под­ни­мет­ся на вы­со­ту шести мет­ров. И днём
сле­ду­ю­ще­го дня она уже ока­жет­ся на вер­ши­не де­ре­ва. Ответ: 7

39. За­да­ние 20 № 506793. Улит­ка
за день за­пол­за­ет вверх по де­ре­ву на 4 м, а за ночь спол­за­ет на 1 м. Вы­со­та
де­ре­ва 13 м. За сколь­ко дней улит­ка впер­вые до­ползёт до вер­ши­ны де­ре­ва?

По­яс­не­ние.
За
день улит­ка за­ползёт на 4 метра, а за ночь спу­стит­ся на 1 метр. Итого за
сутки она под­ни­мет­ся на 3 метра. За трое суток он ока­жет­ся на вы­со­те 9
мет­ров. И во время сле­ду­ю­ще­го дня за­ползёт на вер­ши­ну де­ре­ва. Ответ: 4      ———-  Дуб­ли­ру­ет
за­да­ние 506523.

40. За­да­ние 20 № 506292. Хо­зя­ин
до­го­во­рил­ся с ра­бо­чи­ми, что они вы­ко­па­ют ему ко­ло­дец на сле­ду­ю­щих
усло­ви­ях: за пер­вый метр он за­пла­тит им 4200 руб­лей, а за каж­дый сле­ду­ю­щий
метр — на 1300 руб­лей боль­ше, чем за преды­ду­щий. Сколь­ко денег хо­зя­ин
дол­жен будет за­пла­тить ра­бо­чим, если они вы­ко­па­ют ко­ло­дец глу­би­ной
11 мет­ров?

По­яс­не­ние. По­сле­до­ва­тель­ность
цен за метр — ариф­ме­ти­че­ская про­грес­сия с пер­вым чле­ном  и
раз­но­стью  Сумма
пер­вых  чле­нов
ариф­ме­ти­че­ской про­грес­сии вы­чис­ля­ет­ся по фор­му­ле  В
нашем слу­чае имеем:

Т.о., цена ра­бо­ты со­став­ля­ет 117 700 руб.     Ответ: 117 700.

41. За­да­ние 20 № 506688. Хо­зя­ин
до­го­во­рил­ся с ра­бо­чи­ми, что они ко­па­ют ко­ло­дец на сле­ду­ю­щих усло­ви­ях:
за пер­вый метр он за­пла­тит им 3500 руб­лей, а за каж­дый сле­ду­ю­щий метр —
на 1600 руб­лей боль­ше, чем за преды­ду­щий. Сколь­ко денег хо­зя­ин дол­жен
будет за­пла­тить ра­бо­чим, если они вы­ко­па­ют ко­ло­дец глу­би­ной 9 мет­ров?

По­яс­не­ние.
По­сле­до­ва­тель­ность
цен за метр — ариф­ме­ти­че­ская про­грес­сия с пер­вым эле­мен­том  и
раз­но­стью  Сумма
пер­вых  эле­мен­тов
ариф­ме­ти­че­ской про­грес­сии —  Т.е.
в нашем слу­чае имеем   Ответ: 89100.

—— Дуб­ли­ру­ет за­да­ние 506292.