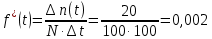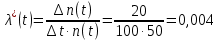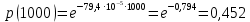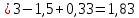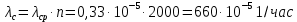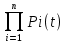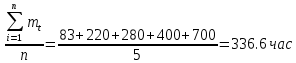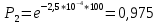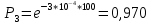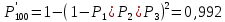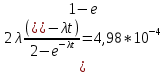Подборка по базе: Практикум Педагогические ситуации и их решение.doc, Трудовые ресурсы. Самостоятельное решение.docx, Вопрос 3. Формирование позитивного имиджа организации работодате, ВЭД решение.docx, Памятка о порядке действий работников в случае возникновения пож, статистика население. задачи решение.docx, Тема 3. Требования нормативных правовых актов к порядку расследо, Задание ос решение.docx, В истории человечества можно найти немало случаев геноцида.docx, ОСР № 2 Решение.docx
54. На испытание поставлено 100 однотипных изделий. За 4000 час. отказало 50 изделий. За интервал времени 4000 — 4100 час. отказало ещё 20 изделий. Требуется определить f*(t), λ*(t) при t=4000 час.
Решение. В данном случае N=100; t=4000 час; Δt =100 час; Δn(t)=20; n(t)=50.
55. На испытание поставлено 100 однотипных изделий. За 4000 час. отказало 50 изделий. Требуется определить p*(t) и q*(t) при t=4000 час.
В данном случае N= 100; n(t)=100-50=50; N-n(t)=100-50=50. По формулам определяем:
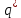

Р(4000)= 50/100=0,5
q(4000)=50/100=0,5
56. В течение 1000 час из 10 гироскопов отказало 2. За интервал времени 1000 — 1100 час. отказал еще один гироскоп. Требуется определить f*(t), λ*(t) при t =1000 час.
В данном случае N=10; t=1000 час; Δt =100 час; Δn(t)=1; n(t)=8.
f*(1000) = 1/ 10*100 = 1*10-2 1/час
λ*(1000) = 1/ 100*8 = 1,25*10 1/час
57. На испытание поставлено 1000 однотипных электронных ламп. За первые 3000 час. отказало 80 ламп. За интервал времени 3000 — 4000 час. отказало еще 50 ламп. Требуется определить p*(t) и q*(t) при t=4000 час.
В данном случае N= 1000; n(t)=1000-80-50=870; N-n(t)=1000-870=130. По формулам определяем:
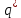


q*(t) = 1000-870/1000=1,3*10-2 1/час
p*(t) = 870/1000=8,7*10-2 1/час
58. На испытание поставлено 1000 изделий. За время t=1300 час. вышло из строя 288 штук изделий. За последующий интервал времени 1300-1400 час. вышло из строя еще 13 изделий. Необходимо вычислить p*(t) при t=1300час.
и t=1400 час.; f*(t), λ *(t) при t =1300 час.
Решение. В данном случае N=1000; t=1300 час; Δt =100 час; Δn(t)=13; n(t)=288; n(1300)=1000-288=712; n(1400)=1000-288-13=699



59. На испытание поставлено 45 изделий. За время t=60 час. вышло из строя 35 штук изделий. За последующий интервал времени 60-65 час. вышло из строя еще 3 изделия. Необходимо вычислить p*(t) при t=60час. и t=65 час.; f*(t), λ *(t) при t =60 час.
Решение. В данном случае N=45; t=60 час; Δt =5 час; Δn(t)=3; n(t)=35; n(60)=45-35=10; n(65)=45-35-3=7



60. В результате наблюдения за 45 образцами радиоэлектронного оборудования, которые прошли предварительную 80-часовую приработку, получены данные до первого отказа всех 45 образцов, сведенные в таблицу. Необходимо определить mt*.
Таблица
| ti,час. | ni | ti,час. | ni | ti,час. | ni |
| 0-10 | 19 | 30-40 | 3 | 60-70 | 1 |
| 10-20 | 13 | 40-50 | 0 | ||
| 20-30 | 8 | 50-60 | 1 |

61. На испытание поставлено 8 однотипных изделий. Получены следующие значения ti (ti — время безотказной работы i-го изделия):
t1 =560час.; t2=700час.; t3 =800час.; t4=650час.; t5=580час.; t6=760час.; t7=920час.; t8=850час.
Определить статистическую оценку среднего времени безотказной работы изделия.
Стат оценка ср вр-ни безотк работы 
62. За наблюдаемый период эксплуатации в аппаратуре было зарегистрировано 6 отказов. Время восстановления составило: t1 =15мин.; t2=20мин.; t3 =10мин.; t4=28мин.; t5=22мин.; t6=30мин.
Требуется определить среднее время восстановления аппаратуры.
Среднее время восстан-ния аппаратуры
63. На испытание поставлено 1000 изделий. За время t=11000 час. вышло из строя 410 изделий. Зв последующий интервал времени 11000-12000 час. вышло из строя еще 40 изделий. Необходимо вычислить p*(t) при t=11000 час. и t=12000 час., а также f*(t), λ *(t) при t=11000 час.
N=1000, T=11000час, Δt=1000час, n(t)=(1000-410)=590, Δn(t)=40.
Решение:
P*(11000)=n(t)/N = 590/1000=0,59
P*(12000)=n(t)/N = 40/1000=0,04
f*(11000)=Δn(t)/N*Δt=40/1000*1000=0,04*10-3 1/час
λ*(е)= Δn(t)/Δt*n(t)=40/1000*590=0,07*10-3 1/час
64. Вероятность безотказной работы автоматической линии изготовления цилиндров автомобильного двигателя в течении 120 час равна 0.9. Предполагается, что справедлив экспоненциальный закон надежности. Требуется рассчитать интенсивность отказов и частоту отказов линии для момента времени t =120 час., а также среднее время безотказной работы.
P=0,9, t=120 час.
Решение:
P(t) = e—λ*t
P(120)= e—λ*120
λ=8,8*10-4 1/час
f(t)=λ(t)*P(t)
f(t)=8,8*10-4*0,9=7,92*10-4
m(t)=1/λ=1/8,8*10-4=1136 час.
65. Среднее время безотказной работы автоматической системы управления равно 640 час. Предполагается, что справедлив экспоненциальный закон надежности. Необходимо определить вероятность безотказной работы в течение 120 час., частоту отказов для момента времени t=120 час и интенсивность отказов.
m(t)=640 час, t=120 час.
Решение:
m(t)=1/λ
λ=1/640=1,56 *10-3 1/час.
P(t) = e—λ*t
P(120)= e—1,56*10-3*120=0,42
f(120)=λ(120)*P(120)
f(120)=1,56*10—3*0,42=0,65*10—3 1/час
66. Время работы изделия подчинено нормальному закону с параметрами mt = 8000 час., σt =1000 час. Требуется вычислить количественные характеристики надежности p(t) , f(t) , λ(t) для t=8000 час.
67. Время исправной работы скоростных шарикоподшипников подчинено закону Вейбулла с параметрами α=2,6 ; λ= 1,65*10-7 1/час.
Требуется вычислить количественные характеристики надежности Р(t), f(t), λ(t) для t=150 час. и среднее время безотказной работы шарикоподшипников.
68. Вероятность безотказной работы изделия в течение t=1000 час. Р(1000)=0,95. Время исправной работы подчинено экспоненциальному закону. Требуется определить количественные характеристики надежности f(t), λ (t), mt.
69. Среднее время исправной работы изделия равно 1260 час. Время исправной работы подчинено экспоненциальному закону. Необходимо найти его количественные характеристики надежности P(t), f(t), λ (t) для t=1000 час.
Дано:
T=1260ч
t=1000ч
p(t)-?
λ(t)-?
f(t)-?
Решение:
1)
2)Варианты безотказной работы
3) Частота отказов
70. В результате анализа данных об отказах изделия установлено, что частота отказов имеет вид f(t)=2e-t (1-e-t) . Необходимо найти количественные характеристики надежности P(t), λ (t), mt.
Дано:
f(t)=2e-t (1-e-t)
p(t)-?
λ(t)-?
mt-?
Решение:
1)
=1-2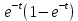
2) 
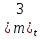

71. В результате анализа данных об отказах изделий установлено, что вероятность безотказной работы выражается формулой P(t)=3e-t-3e-2t+e-3t.
Требуется найти количественные характеристики надежности P(t), λ (t), mt.
Дано:
f(t)=
p(t)-?
λ(t)-?
mt-?
Решение:
1)
2)
3)
72. Определить вероятность безотказной работы и интенсивность отказов прибора при t = 1300 часов работы, если при испытаниях получено значение среднего времени безотказной работы mt=1500 час. и среднее квадратическое отклонение σt = 100 час.
Дано: t=1300 ; mt=1500 час;
Решение: по эксп. закону 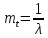

По нормальному закону: 
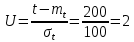


λ(t) = f(t)/P(t) = 0,0024 1/час
73. Аппаратура связи состоит из 2000 элементов, средняя интенсивность отказов которых λ ср= 0,33 * 10-5 1/час.
Необходимо определить вероятность безотказной работы аппаратуры в течении t = 200 час и среднее время безотказной работы аппаратуры.
Дано: n=2000 эл; λ ср= 0,33 * 10-5 1/час; P(200) -?; mt=?
Решение:
74. Невосстанавливаемая в процессе работы электронная машина состоит из 200000 элементов, средняя интенсивность отказов которых λ =0,2 * 10-6 1/час. Требуется определить вероятность безотказной работы электронной машины в течении t = 24 часа и среднее время безотказной работы электронной машины.
Дано: n=200000 эл; λ ср= 0,2 * 10-6 1/час; P(24) -?; mt=?
Решение:
75. Система управления состоит из 6000 элементов, средняя интенсивность отказов которых λ ср. = 0,16*10-6 1/час. Необходимо определить вероятность безотказной работы в течении t = 50 час и среднее время безотказной работы.
Дано:
n= 6000
λср=0.16*10-6 1/час
p(50)-?
mt-?
Решение:
1) λс = λср * n = 0.16*10-6 *6000 = 960*10-6 1/час
2)
3)
76. Прибор состоит из n = 5 узлов. Надежность узлов характеризуется вероятностью безотказной работы в течение времени t , которая равна: P1(t)=0,98; P2(t)=0,99; P3(t)=0,998; P4(t)=0,975; P5(t)=0,985. Необходимо определить вероятность безотказной работы прибора.
Дано:
n = 5
P1(t)=0,98
P2(t)=0,99
P3(t)=0,998
P4(t)=0,975
P5(t)=0,985
Pс(t)= ?
Решение:
При последовательном соединении: Pс(t)=
Pс(t)= P1(t)*P2(t)*P3(t)*P4(t)*P5(t)
Pс(t)= 0,98*0,99*0,998*0,975*0,985=0.9299
77. Система состоит из пяти приборов, среднее время безотказной работы которых равно: mt1=83 час; mt2=220 час; mt3=280 час; mt4=400 час; mt5=700 час. Для приборов справедлив экспоненциальный закон надежности. Требуется найти среднее время безотказной работы системы.
Дано:
n=5
mt1=83 час
mt2=220 час
mt3=280 час
mt4=400 час
mt5=700 час
mср=?
Решение:
Экспоненциальный закон надежности: mср=1/λ
Среднее время безотказной работы системы:
mcр =
78. Прибор состоит из пяти блоков. Вероятность безотказной работы каждого блока в течение времени t=50 час равна: P1(50)=0,98; Р2(50)=0,99; Р3(50)=0,998; Р4(50)=0,975; Р5(50)=0,985. Справедлив экспоненциальный закон надежности. Требуется найти среднее время безотказной работы прибора.
Решение:
Найдем вероятность безотказной работы системы Рс(t)=
Pc(50)=0,98*0,99*0,998*0,975*0,985=0,929
Исходя из экспоненциального закона, найдем интенсивность отказов
Найдем среднюю наработку до первого отказа
Средняя наработка до первого отказа равна 675 часов.
79. Приемник состоит из трех блоков: УВЧ, УПЧ и УНЧ. Интенсивности отказов этих блоков соответственно равны: λ1=4*10-4 1/час; λ2=2,5*10-4 1/час; λ3=3*10-4 1/час. Требуется рассчитать вероятность безотказной работы приемника при t=100 час для следующих случаев: а) резерв отсутствует; б) имеется общее дублирование приемника в целом.
а) Р(100)=Р1*Р2*Р3=0,909
б) m=2
80. В радиопередатчике, состоящем из трех равнонадежных каскадов (n=3) применено общее постоянное дублирование всего радиопередатчика. Интенсивность отказов каскада равна λ=5*10-4 1/час. Определить Рс(t), mtc, fc(t), λc(t) радиопередатчика с дублированием.
Рс(t)=1-(1-e—λnt)2
Pc(t)=
mtc=
mtc=
fc(t)=2λ*e-λt(1-e-λt)=2*5*10-4
λc(t)=
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Воронежский государственный технический университет»
Кафедра автоматизированного оборудования машиностроительного производства
ДИАГНОСТИКА СТАНКОВ С ПОМОЩЬЮ НЕЙРОННЫХ СЕТЕЙ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к выполнению практических работ для студентов направления 15.04.01 «Машиностроение»
(программа магистерской подготовки «Обеспечение качественно-точностных характеристик при изготовлении изделий в автоматизированном машиностроительном производстве»)
всех форм обучения
Воронеж 2021
1
УДК 621.01(07) ББК 34.5я7
Составитель д-р техн. наук, проф. С. Ю. Жачкин
Диагностика станков с помощью нейронных сетей: методические ука-
зания к выполнению практических работ для студентов направления 15.04.01 «Машиностроение» (программа магистерской подготовки «Обеспечение качественно-точностных характеристик при изготовлении изделий
вавтоматизированном машиностроительном производстве») всех форм обучения / ФГБОУ ВО «Воронежский государственный технический университет»; сост.: С. Ю. Жачкин. — Воронеж: Изд-во ВГТУ, 2021.- 18 с.
Вметодических указаниях изложены требования и общие вопросы по выполнению практических работ, рассматривается сценарный анализ и расчет сложных технических систем, объектов на предмет локальных предельных состояний.
Предназначены для студентов направления 15.04.01 «Машиностроение» всех форм обучения.
Методические указания подготовлены в электронном виде и содержатся
вфайле МУ_ ДСсПНС_ПР.pdf.
Ил. 3. Табл. 5. Библиогр.: 8 назв.
УДК 621.01(07) ББК 34.5 я7
Рецензент – С. Н. Яценко, канд. физ.-мат. наук, доц. кафедры автоматизированного оборудования машиностроительного производства ВГТУ
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
Практическая работа № 1
Определение единичных показателей надежности невосстанавливаемых объектов
Цель: научить студентов определять показатели безотказности по статистическим данным
Задачи обучения:
ознакомить с показателями безотказности и основными методами их определения;
привить навыки определения показателей безотказности невосстанавливаемых объектов;
обучить давать характеристику находимых показателей безотказности.
Методы и формы обучения и преподавания: индивидуальная работа,
работа в парах; ситуационные задачи.
Материальнотехническое оснащение:
Калькулятор или компьютер с программами EXCEL.
Задания и методические указания к их выполнению:
Работа студента на занятии оценивается в 1-3 балла в зависимости от его активности при решении задач и ответах на поставленные преподавателем вопросы.
Примеры выполнения задания
Пример 1.1. На промысловые испытания поставлено 60 буровых лебедок. Испытания проводились в течение 2000 часов. В ходе испытаний отказало 6 буровых лебедок. Определить статистическую оценку вероятности безотказной работы изделий за время 2000 часов.
Решение.
Вероятность безотказной работы R(t1, t2) – вероятность выполнить требуемую функцию при данных условиях в интервале времени (t1, t2). Вероятность безотказной работы определяется в предположении, что в начале интервала времени (момент начала исчисления наработки) изделие находится в работоспособном состоянии.
Статистическая оценка вероятности безотказной работы определяется по формуле
|
~ |
t 1 |
n t |
, |
|
|
R |
||||
|
N |
где N – число объектов, работоспособных в начальный момент времени; п(t) – число объектов, отказавших на отрезке от 0 до t.
3
Подставляем исходные данные в формулу
|
~ |
n t |
6 |
||||
|
R t 1 |
1 |
0,9 . |
||||
|
N |
60 |
|||||
|
Ответ. Вероятность безотказной работы |
~ |
|||||
|
R t 0,9 . Вероятность безотказной ра- |
боты является:
—показателем безотказности;
—единичным, так как характеризует только одно свойств – безотказность;
—экспериментальным, так как определяется по результатам испытаний;
—групповым, так как характеризует надежность партии изделий.
Пример 1.2. На промысловые испытания поставлено 60 буровых лебедок. Испытания проводились в течение 2000 часов. Зафиксированы отказы буровых лебедок в моменты времени t1 = 1210 ч; t2 = 480 ч; t3 = 900 ч; t4 = 700 ч; t5 = 1900
ч; t6 = 1100 ч; остальные буровые лебедки не отказали. Найти статистическую оценку среднего значения наработки до первого отказа.
Решение:
Средняя наработка до первого отказа – это математическое ожидание наработки по первого отказа.
Средняя наработка до первого отказа по статистическим данным определяется по формуле
|
~ |
1 |
N |
1 |
1210 |
1100 2000 54 1904,83÷~ 1905 ч |
|||||
|
0 |
ti |
480 |
900 |
700 1900 |
||||||
|
N i 1 |
60 |
Ответ: Средняя наработка до первого отказ Т0 = 1905 ч. Средняя наработка до первого отказа является:
—показателем безотказности;
—единичным, так как характеризует только одно свойств – безотказность;
—экспериментальным, так как определяется по результатам испытаний;
—групповым, так как характеризует надежность партии изделий.
Задания для самостоятельной работы
Задача 1.1. На испытание поставлено 200 однотипных изделий. За 2000 ч отказало 50 изделий. За последующие 100 часов отказало ещё 5 изделий. Требуется определить:
1.статистическую оценку вероятности безотказной работы за время работы t1 = 2000 час и t2 = 2100 час;
2.статистическую оценку вероятности отказа за время работы t1 = 2000 час и t2
= 2100 час;
3.оценку плотности распределения отказов и интенсивности отказов в промежутке времени между t1 = 2000 час и t2 = 2100 час.
4
Задача 1.2. На испытание поставлено 100 однотипных изделий. За 4000 часов работы отказало 50 изделий. Определить статистические оценки вероятности безотказной работы и вероятности отказа за время работы 4000 часов.
Задача 1.3. На испытание поставлено 100 однотипных изделий. За 4000 часов работы отказало 50 изделий. За последующие 50 часов еще 5 изделий. Дать оценку плотности распределения отказов и интенсивности отказов в промежутке времени между t1 = 4000 час и t2 = 4050 час.
Задача 1.4. В течение 500 часов работы из 20 буровых насосов отказало 2. За интервал времени 500 – 520 часов отказал еще один буровой насос. Дать оценку плотности распределения отказов и интенсивности отказов в промежутке времени между t1 = 500 час и t2 = 520 час.
Задача 1.5. На испытание поставлено 2000 подшипников качения. За первые 3000 часов отказало 80 изделий. За интервал времени 3000 – 4000 часов отказало еще 50 подшипников. Требуется определить статистическую оценку вероятности безотказной работы за время 4000 часов.
Задача 1.6. В течение 500 часов работы из 20 буровых насосов отказало 2. За интервал времени 500 – 520 часов отказал еще один буровой насос. Требуется определить статистическую оценку вероятности отказа за время 520 часов.
Задача 1.7. На испытание поставлено 600 изделий. За время 1200 часов вышло из строя 125 штук изделий. За последующий интервал времени 1200 – 1250 часов вышло из строя еще 13 изделий. Необходимо определить статистическую оценку вероятности безотказной работы и вероятности отказа за время работы t1 = 1200 час и t2 = 1250 час; оценку плотности распределения отказов и интенсивности отказов в промежутке времени между t1 = 1200 час и t2 = 1250 час.
Задача 1.8. На испытание поставлено 10 однотипных изделий. Получены следующие значения времени безотказной работы: t1 = 580 час; t2 = 720 час; t3 =
860 час; t4 = 550 час; t5 = 780 час; t6 = 830 час; t7 = 910 час; t8 = 850 час; t9 = 840
час; t10 = 750 час. Определить статистическую оценку среднего времени безотказной работы изделия.
Контрольные вопросы:
1.Что такое безотказность?
2.Какие показатели надежности являются показателями безотказности?
3.Что такое вероятность безотказной работы?
4.Что такое вероятность отказа?
5.Как определяются статистические оценки вероятности безотказной работы и вероятности отказа?
6.Как определяется плотность распределения наработки?
7.Что такое интенсивность отказов?
8.Кривая зависимости интенсивности отказа во времени.
5
9. Дайте определение средней наработки до отказа и средней наработки до первого отказа.
Практическая работа № 2 Определение показателей безотказности невосстанавливаемых объектов
по статистическим данным
Цель: научить студентов определять показатели безотказности по статистическим данным
Задачи обучения:
ознакомить с методикой определения показателей безотказности по статистическим данным на определенном промежутке времени;
привить навыки построения зависимостей показателей безотказности во времени;
обучить давать характеристику находимых показателей безотказности.
Методы и формы обучения и преподавания: индивидуальная работа,
работа в парах; ситуационные задачи, выполнение домашних заданий.
Материальнотехническое оснащение:
Калькулятор или компьютер с программами EXCEL или MathCAD.
Задания и методические указания к их выполнению (алгоритм, форма, сроки отчетности, критерии оценивания):
На основе представленных статистических данных провести расчет и анализ показателей надежности серии невосстанавливаемых объектов.
Пример выполнения задания
Исходные данные: Число изделий, поставленных на испытание, N = 1000 изделий. Испытания проводятся в течение 100 часов. Каждые сто часов определялось количество отказов изделий. Результаты испытаний представлены в таблице 1.
Задание:
1.Найти статистическую оценку распределения вероятностей отказа Q(t) и безотказной работы R(t) во времени.
2.Найти изменение плотности вероятности отказов f(t) и интенсивности отказов λ(t) по времени.
3.Результаты расчета отразить на графиках.
Решение.
6

1.Определяем количество работоспособных изделий на конец каждого периода по формуле
N t N n t
2.Определяем статистическую оценку вероятности безотказной работы на конец каждого периода по формуле
|
~ |
n t |
N t |
|||||
|
R t 1 |
. |
||||||
|
N |
N |
3.Определяем количество отказавших деталей нарастающим итогом на конец каждого периода по формуле
n ti 1 n t n t
4.Определяем статистическую оценку вероятности отказа на конец каждого периода по формуле
Q t
~ n t .
N
5.Определяем статистическую оценку плотности вероятности отказов по формуле
~ n t . f t
N t
6. Определяем значение интенсивности отказов по формуле
7. Результаты расчета для удобства сводим в таблицу 1
8. По данным расчета строим графики зависимости расчетных величин по времени (рис. 1-3)
7

Таблица 1 Результаты расчета статистических оценок показателей безотказности
|
Вре- |
Коли- |
Количе- |
Коли- |
Веро- |
Веро- |
Плот- |
Интен- |
|
|
мен- |
чество |
ство рабо- |
чество |
ятность |
ятность |
ность |
сивность |
|
|
ной |
отказов |
тоспособ- |
отка- |
безот- |
отказа |
вероят- |
отказов |
|
|
интер- |
за дан- |
ных изде- |
завших |
казной |
Q(t) |
ности |
λ(t), ·10-2 |
|
|
вал Δt, |
ный |
лий на ко- |
изде- |
работы |
отказов |
|||
|
час |
интер- |
нец перио- |
лий на |
R(t) |
f(t), |
|||
|
вал |
да N(t) |
конец |
-2 |
|||||
|
n(t) |
перио- |
·10 |
||||||
|
да |
||||||||
|
1000 |
||||||||
|
0 – 100 |
0,000526 |
|||||||
|
50 |
950 |
50 |
0,95 |
0,05 |
0,0005 |
32 |
||
|
100 – |
0,000439 |
|||||||
|
200 |
40 |
910 |
90 |
0,91 |
0,09 |
0,0004 |
56 |
|
|
200 – |
0,000224 |
|||||||
|
300 |
20 |
890 |
110 |
0,89 |
0,11 |
0,0002 |
72 |
|
|
300 – |
0,000229 |
|||||||
|
400 |
20 |
870 |
130 |
0,87 |
0,13 |
0,0002 |
89 |
|
|
400 – |
0,000116 |
|||||||
|
500 |
10 |
860 |
140 |
0,86 |
0,14 |
0,0001 |
28 |
|
|
500 – |
0,000886 |
|||||||
|
600 |
70 |
790 |
210 |
0,79 |
0,21 |
0,0007 |
08 |
|
|
600 – |
0,001617 |
|||||||
|
700 |
110 |
680 |
320 |
0,68 |
0,32 |
0,0011 |
65 |
|
|
700 – |
||||||||
|
800 |
280 |
400 |
600 |
0,4 |
0,6 |
0,0028 |
0,007 |
|
|
800 – |
0,016666 |
|||||||
|
900 |
250 |
150 |
850 |
0,15 |
0,85 |
0,0025 |
67 |
|
|
900 – |
||||||||
|
1000 |
150 |
0 |
1000 |
0 |
1 |
0,0015 |
Рис. 1. График зависимости вероятности безотказной работы и вероятности отказа от времени
8
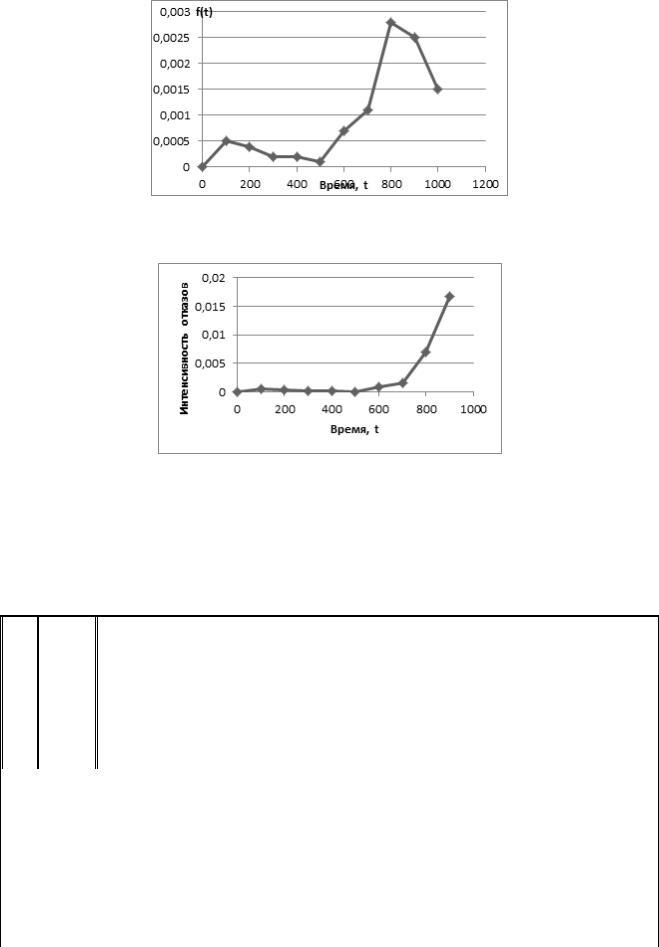
Рис. 2. График зависимости плотности распределения отказов во времени
Рис. 3. График зависимости интенсивности отказов от времени
Исходные данные для выполнения задания представлены в виде таб. 2.
Таблица 2 Исходные данные для выполнения задания по практической работе № 2
НОбКоличество отказавших изделий за интервал времени ti, шт.
|
ом |
щее |
0 – |
100 – |
200 – |
300 – |
||||||
|
ер |
кол- |
100 |
200 |
300 |
400 |
500 |
900 |
||||
|
ва |
во |
400 – |
600 – |
700 – |
800 – |
||||||
|
– |
– |
||||||||||
|
ри |
изде- |
500 |
700 |
800 |
900 |
||||||
|
600 |
1000 |
||||||||||
|
ан |
де- |
||||||||||
|
та |
лий |
||||||||||
|
1 |
1000 |
30 |
170 |
50 |
20 |
30 |
20 |
280 |
200 |
70 |
130 |
|
2 |
2500 |
80 |
320 |
300 |
20 |
80 |
600 |
600 |
110 |
210 |
200 |
|
3 |
3000 |
100 |
500 |
200 |
10 |
90 |
100 |
100 |
600 |
100 |
500 |
|
4 |
5100 |
150 |
950 |
200 |
100 |
50 |
190 |
1360 |
1100 |
250 |
750 |
|
5 |
1150 |
50 |
180 |
60 |
20 |
35 |
25 |
330 |
220 |
50 |
170 |
|
6 |
7300 |
124 |
206 |
||||||||
|
0 |
370 |
140 |
230 |
140 |
0 |
1450 |
450 |
1000 |
1240 |
||
|
7 |
8300 |
250 |
1410 |
420 |
170 |
250 |
160 |
2320 |
1660 |
420 |
1240 |
9
|
8 |
300 |
9 |
51 |
15 |
6 |
9 |
6 |
84 |
60 |
15 |
45 |
|
9 |
1000 |
30 |
170 |
50 |
30 |
20 |
20 |
180 |
300 |
140 |
60 |
|
10 |
300 |
9 |
51 |
15 |
9 |
6 |
6 |
54 |
90 |
42 |
18 |
|
11 |
700 |
22 |
117 |
38 |
20 |
12 |
13 |
143 |
195 |
98 |
42 |
|
12 |
6700 |
200 |
1140 |
260 |
270 |
140 |
134 |
1206 |
2010 |
890 |
450 |
|
13 |
3700 |
110 |
630 |
190 |
110 |
70 |
80 |
660 |
1110 |
520 |
220 |
|
14 |
1200 |
40 |
200 |
60 |
36 |
24 |
24 |
216 |
360 |
168 |
72 |
|
15 |
1800 |
60 |
300 |
90 |
60 |
30 |
36 |
324 |
540 |
252 |
108 |
|
16 |
1300 |
34 |
224 |
66 |
30 |
14 |
16 |
276 |
380 |
186 |
74 |
|
17 |
1330 |
||||||||||
|
0 |
390 |
2270 |
510 |
530 |
270 |
258 |
2402 |
4010 |
1770 |
890 |
|
|
18 |
7300 |
210 |
1250 |
370 |
210 |
130 |
150 |
1310 |
2210 |
1030 |
430 |
|
19 |
2300 |
70 |
390 |
110 |
62 |
38 |
38 |
422 |
710 |
326 |
134 |
|
20 |
3500 |
110 |
590 |
170 |
110 |
50 |
62 |
638 |
1070 |
494 |
206 |
Контрольные вопросы:
1.Свойства функции вероятности безотказной работы?
2.Свойства функции вероятности отказа?
3.Каким образом определяется плотность распределения наработки во времени?
4.Кривая зависимости интенсивности отказа во времени.
5.Кривая плотности распределения отказов во времени
Практическая работа № 3
Определение единичных и комплексных показателей восстанавливаемых объектов
Цель: научить студентов определять показатели надежности по статистическим данным
Задачи обучения:
ознакомить с методикой определения единичных и комплексных показателей по статистическим данным;
привить навыки расчета показателей надежности;
обучить давать характеристику находимых показателей надежности.
Методы и формы обучения и преподавания: индивидуальная работа,
работа в парах; ситуационные задачи.
Материальнотехническое оснащение:
Калькулятор или компьютер с программами EXCEL или MathCAD.
10
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
На испытание поставлено N0 =1000 изделий. За время t =1000 час вышло из строя n(t)= 160 шт изделий. За последующий интервал времени Δt = 1000ч вышло из строя n (Δt) =50 изделий.
Необходимо вычислить вероятность безотказной работы за время t и t + Δt , частоту отказов и интенсивность отказов на интервале Δt.
Вероятность безотказной работы на основании статистических данных определяется по выражению
P*(t)=N0-n(t)N0, (1)
где N0 – количество элементов в начале испытаний ,шт;
n (t) – количество отказавших элементов на интервале времени
t , шт ,
Определяем вероятность безотказной работы на момент времени t=1000ч , N0 =1000шт, n (t) =160 шт:
P*(1000)=1000-1601000 =0,84
Для интервала t +Δt = 2000ч n(2000) = n(1000) +n (1000) = 160+50=210 шт :
P*(2000)=1000-2101000 =0,79
Частота отказов a*(t) по статистическим данным об отказах оценивается согласно выражению:
a*(t)=n(∆t)N0∙∆t, (2)
где n (Δt) — количество отказавших изделий в интервале времени
от t – Δt/2 до t + Δt/2 ; n (Δt) =50 шт
N0 — первоначальное количество испытываемых объектов, шт
Δt – величина интервала,ч ; Δt =1000ч
a*(1500) =501000∙1000 =0,5∙10-4 1/ч
Интенсивность отказов λ*(t) по статистическим данным об отказах определяется по формуле:
λ*(t)=n(∆t)nср∙∆t , (3)
где n (Δt) — количество отказавших изделий в интервале времени
от t – Δt/2 до t + Δt/2 ; n (Δt) =15 шт
nср — среднее число исправно работающих изделий в
интервале Δt,шт
Cреднее число изделий, исправно работающих в интервале от 1000 до 2000ч:
nср=ni+ni+12 , (4)
где ni – количество изделий, исправно работающих в начале
рассматриваемого интервала , шт ni =840 шт
ni +1 – количество изделий, исправно работающих в конце
рассматриваемого интервала , шт ni +1 = 840-50=790 шт
nср=840+7902 = 815 шт ,
λ*(1500)= 50815∙1000 =0,6∙10-4 1/ч
Ответ: P*(1000)=0,84; P*(2000)=0,79
a*(1500) =0,5∙10-4 1/ч ; λ*(1500)=0,6∙10-4 1/ч
Самостоятельная работа № 1
«Определение единичных показателей надежности невосстанавливаемых объектов»
Цель: научить студентов определять показатели безотказности по статистическим данным
Задание: Решить задачи согласно выбранного уровня и ответить на контрольные вопросы
Примеры решения
Пример 1.1. На промысловые испытания поставлено 60 буровых лебедок. Испытания проводились в течение 2000 часов. В ходе испытаний отказало 6 буровых лебедок. Определить статистическую оценку вероятности безотказной работы изделий за время 2000 часов.
Решение.
Вероятность безотказной работы R(t1, t2) – вероятность выполнить требуемую функцию при данных условиях в интервале времени (t1, t2). Вероятность безотказной работы определяется в предположении, что в начале интервала времени (момент начала исчисления наработки) изделие находится в работоспособном состоянии.
Статистическая оценка вероятности безотказной работы определяется по формуле
,
где N – число объектов, работоспособных в начальный момент времени;
п(t) – число объектов, отказавших на отрезке от 0 до t.
Подставляем исходные данные в формулу (1.1)
.
Ответ. Вероятность безотказной работы . Вероятность безотказной работы является:
— показателем безотказности;
— единичным, так как характеризует только одно свойств – безотказность;
— экспериментальным, так как определяется по результатам испытаний;
— групповым, так как характеризует надежность партии изделий.
Пример 1.2. На промысловые испытания поставлено 60 буровых лебедок. Испытания проводились в течение 2000 часов. Зафиксированы отказы буровых лебедок в моменты времени t1 = 1210 ч; t2 = 480 ч; t3 = 900 ч; t4 = 700 ч; t5 = 1900 ч; t6 = 1100 ч; остальные буровые лебедки не отказали. Найти статистическую оценку среднего значения наработки до первого отказа.
Решение:
Средняя наработка до первого отказа – это математическое ожидание наработки по первого отказа.
Средняя наработка до первого отказа по статистическим данным определяется по формуле
~ 1905 ч
Ответ: Средняя наработка до первого отказ Т0 = 1905 ч. Средняя наработка до первого отказа является:
— показателем безотказности;
— единичным, так как характеризует только одно свойств – безотказность;
— экспериментальным, так как определяется по результатам испытаний;
— групповым, так как характеризует надежность партии изделий.
Пример 1.3. На испытания поставили 200 изделий. За 100 часов работы отказало 25 изделий. За последующие 10 часов отказало еще 7 изделий. Определить статистическую оценку вероятности безотказной работы и вероятности отказа на моменты времени t1 = 100 ч и t2 = 110 ч, оценку плотности распределения отказов и интенсивности отказов в промежутке времени между t1 = 100 ч и t2 = 110 ч.
Решение. Статистическую оценку вероятности безотказной работы на момент времени t1 = 100 ч определяем по формуле
;
Определяем количество отказавших изделий на момент времени t2 = 110 ч
изд.
и вероятность безотказной работы на момент времени t2 = 110 ч
.
Статистическая оценка вероятности отказа на соответствующие моменты времени определяется по формуле (1.2)
,
.
Плотность распределения отказов во времени определяем по формуле (1.3)
1/ч.
Оценку интенсивности отказов можно определить по формуле (1.4)
1/ч.
Ответ: ;
;
;
;
1/ч;
1/ч. Данные показатели являются:
— показателями безотказности;
— единичными, так как характеризуют только одно свойств – безотказность;
— экспериментальными, так как определяются по результатам испытаний;
— групповыми, так как характеризуют надежность партии изделий.
Задания для самостоятельной работы
Уровень А
Задача 1. На испытание поставлено 200 однотипных изделий. За 2000 ч отказало 50 изделий. За последующие 100 часов отказало ещё 5 изделий. Требуется определить:
1. статистическую оценку вероятности безотказной работы за время работы t1 = 2000 час и t2 = 2100 час;
2. статистическую оценку вероятности отказа за время работы t1 = 2000 час и t2 = 2100 час;
3. оценку плотности распределения отказов и интенсивности отказов в промежутке времени между t1 = 2000 час и t2 = 2100 час.
Задача 2. На испытание поставлено 100 однотипных изделий. За 4000 часов работы отказало 50 изделий. Определить статистические оценки вероятности безотказной работы и вероятности отказа за время работы 4000 часов.
Задача 3. На испытание поставлено 100 однотипных изделий. За 4000 часов работы отказало 50 изделий. За последующие 50 часов еще 5 изделий. Дать оценку плотности распределения отказов и интенсивности отказов в промежутке времени между t1 = 4000 час и t2 = 4050 час.
УРОВЕНЬ В
Задача 1. В течение 500 часов работы из 20 буровых насосов отказало 2. За интервал времени 500 – 520 часов отказал еще один буровой насос. Дать оценку плотности распределения отказов и интенсивности отказов в промежутке времени между t1 = 500 час и t2 = 520 час.
Задача 2. На испытание поставлено 2000 подшипников качения. За первые 3000 часов отказало 80 изделий. За интервал времени 3000 – 4000 часов отказало еще 50 подшипников. Требуется определить статистическую оценку вероятности безотказной работы за время 4000 часов.
УРОВЕНЬ С
Задача 1 На испытание поставлено 600 изделий. За время 1200 часов вышло из строя 125 штук изделий. За последующий интервал времени 1200 – 1250 часов вышло из строя еще 13 изделий. Необходимо определить статистическую оценку вероятности безотказной работы и вероятности отказа за время работы t1 = 1200 час и t2 = 1250 час; оценку плотности распределения отказов и интенсивности отказов в промежутке времени между t1 = 1200 час и t2 = 1250 час.
Задача 3 На испытание поставлено 10 однотипных изделий. Получены следующие значения времени безотказной работы: t1 = 580 час; t2 = 720 час; t3 = 860 час; t4 = 550 час; t5 = 780 час; t6 = 830 час; t7 = 910 час; t8 = 850 час; t9 = 840 час; t10 = 750 час. Определить статистическую оценку среднего времени безотказной работы изделия.
Контрольные вопросы:
- Что такое безотказность?
- Какие показатели надежности являются показателями безотказности?
- Что такое вероятность безотказной работы?
- Что такое вероятность отказа?
- Как определяются статистические оценки вероятности безотказной работы и вероятности отказа?
- Как определяется плотность распределения наработки?
- Что такое интенсивность отказов?
- Кривая зависимости интенсивности отказа во времени.
- Дайте определение средней наработки до отказа и средней наработки до первого отказа.
Литература:
- Острейковский В.А. Теория надежности: учебник для вузов. – 2-е изд., испр. – М.: Высшая школа, 2008. – 464 с.;
Самостоятельная работа № 2
«Определение показателей безотказности невосстанавливаемых объектов по статистическим данным»
Цель: научить студентов определять показатели безотказности по статистическим данным
Задания
На основе представленных статистических данных провести расчет и анализ показателей надежности серии невосстанавливаемых объектов.
Пример выполнения задания
Исходные данные: Число изделий, поставленных на испытание, N = 1000 изделий. Испытания проводятся в течение 100 часов. Каждые сто часов определялось количество отказов изделий. Результаты испытаний представлены в таблице 2.1.
Задание:
1. Найти статистическую оценку распределения вероятностей отказа Q(t) и безотказной работы R(t) во времени.
2. Найти изменение плотности вероятности отказов f(t) и интенсивности отказов λ(t) по времени.
3. Результаты расчета отразить на графиках.
Решение.
- Определяем количество работоспособных изделий на конец каждого периода по формуле
- Определяем статистическую оценку вероятности безотказной работы на конец каждого периода по формуле
.
- Определяем количество отказавших деталей нарастающим итогом на конец каждого периода по формуле
- Определяем статистическую оценку вероятности отказа на конец каждого периода по формуле
.
- Определяем статистическую оценку плотности вероятности отказов по формуле
.
- Определяем значение интенсивности отказов по формуле
- Результаты расчета для удобства сводим в таблицу 2.1
- По данным расчета строим графики зависимости расчетных величин по времени (рисунки 1.1, 1.2, 1.3)
Таблица 2.1 – Результаты расчета статистических оценок показателей безотказности
|
Временной интервал Δt, час |
Количество отказов за данный интервал Δn(t) |
Количество работоспособных изделий на конец периода N(t) |
Количество отказавших изделий на конец периода |
Вероятность безотказной работы R(t) |
Вероятность отказа Q(t) |
Плотность вероятности отказов f(t), ·10-2 |
Интенсивность отказов λ(t), ·10-2 |
|
1000 |
|||||||
|
0 – 100 |
50 |
950 |
50 |
0,95 |
0,05 |
0,0005 |
0,00052632 |
|
100 – 200 |
40 |
910 |
90 |
0,91 |
0,09 |
0,0004 |
0,00043956 |
|
200 – 300 |
20 |
890 |
110 |
0,89 |
0,11 |
0,0002 |
0,00022472 |
|
300 – 400 |
20 |
870 |
130 |
0,87 |
0,13 |
0,0002 |
0,00022989 |
|
400 – 500 |
10 |
860 |
140 |
0,86 |
0,14 |
0,0001 |
0,00011628 |
|
500 – 600 |
70 |
790 |
210 |
0,79 |
0,21 |
0,0007 |
0,00088608 |
|
600 – 700 |
110 |
680 |
320 |
0,68 |
0,32 |
0,0011 |
0,00161765 |
|
700 – 800 |
280 |
400 |
600 |
0,4 |
0,6 |
0,0028 |
0,007 |
|
800 – 900 |
250 |
150 |
850 |
0,15 |
0,85 |
0,0025 |
0,01666667 |
|
900 – 1000 |
150 |
0 |
1000 |
0 |
1 |
0,0015 |
Рисунок 2.1 – График зависимости вероятности безотказной работы и вероятности отказа от времени
Рисунок 2.2 – График зависимости плотности распределения отказов во времени
Рисунок 2.3 – График зависимости интенсивности отказов от времени
Таблица 2.2 – Исходные данные для выполнения домашнего задания по практической работе № 2
|
Номер варианта |
Общее кол-во изделий |
Количество отказавших изделий за интервал времени ti, шт. |
|||||||||
|
0 – 100 |
100 – 200 |
200 – 300 |
300 – 400 |
400 – 500 |
500 – 600 |
600 – 700 |
700 – 800 |
800 – 900 |
900 – 1000 |
||
|
1 |
1000 |
30 |
170 |
50 |
20 |
30 |
20 |
280 |
200 |
70 |
130 |
|
2 |
2500 |
80 |
320 |
300 |
20 |
80 |
600 |
600 |
110 |
210 |
200 |
|
3 |
3000 |
100 |
500 |
200 |
10 |
90 |
100 |
100 |
600 |
100 |
500 |
|
4 |
5100 |
150 |
950 |
200 |
100 |
50 |
190 |
1360 |
1100 |
250 |
750 |
|
5 |
1150 |
50 |
180 |
60 |
20 |
35 |
25 |
330 |
220 |
50 |
170 |
|
6 |
7300 |
1240 |
370 |
140 |
230 |
140 |
2060 |
1450 |
450 |
1000 |
1240 |
|
7 |
8300 |
250 |
1410 |
420 |
170 |
250 |
160 |
2320 |
1660 |
420 |
1240 |
|
8 |
300 |
9 |
51 |
15 |
6 |
9 |
6 |
84 |
60 |
15 |
45 |
|
9 |
1000 |
30 |
170 |
50 |
30 |
20 |
20 |
180 |
300 |
140 |
60 |
|
10 |
300 |
9 |
51 |
15 |
9 |
6 |
6 |
54 |
90 |
42 |
18 |
|
11 |
700 |
22 |
117 |
38 |
20 |
12 |
13 |
143 |
195 |
98 |
42 |
|
12 |
6700 |
200 |
1140 |
260 |
270 |
140 |
134 |
1206 |
2010 |
890 |
450 |
|
13 |
3700 |
110 |
630 |
190 |
110 |
70 |
80 |
660 |
1110 |
520 |
220 |
|
14 |
1200 |
40 |
200 |
60 |
36 |
24 |
24 |
216 |
360 |
168 |
72 |
|
15 |
1800 |
60 |
300 |
90 |
60 |
30 |
36 |
324 |
540 |
252 |
108 |
|
16 |
1300 |
34 |
224 |
66 |
30 |
14 |
16 |
276 |
380 |
186 |
74 |
|
17 |
13300 |
390 |
2270 |
510 |
530 |
270 |
258 |
2402 |
4010 |
1770 |
890 |
|
18 |
7300 |
210 |
1250 |
370 |
210 |
130 |
150 |
1310 |
2210 |
1030 |
430 |
|
19 |
2300 |
70 |
390 |
110 |
62 |
38 |
38 |
422 |
710 |
326 |
134 |
|
20 |
3500 |
110 |
590 |
170 |
110 |
50 |
62 |
638 |
1070 |
494 |
206 |
Контрольные вопросы:
- Свойства функции вероятности безотказной работы?
- Свойства функции вероятности отказа?
- Каким образом определяется плотность распределения наработки во времени?
- Кривая зависимости интенсивности отказа во времени.
- Кривая плотности распределения отказов во времени
Литература:
- Острейковский В.А. Теория надежности: учебник для вузов. – 2-е изд., испр. – М.: Высшая школа, 2008. – 464 с.;
Самостоятельная работа № 3
«Определение единичных и комплексных показателей восстанавливаемых объектов»
Цель: научить студентов определять показатели надежности по статистическим данным
Примеры решения
Пример 3.1. На промысловые испытания поставлено 3 буровых насоса. В ходе испытаний у первого насоса было зафиксировано 144 отказа, у второго – 160 отказов, у третьего – 157 отказов. Суммарная наработка на отказ для первого насоса составила 3250 часов, для второго – 3600 часов, для третьего – 2800 часов. Определить среднюю наработку до отказа и средний ресурс бурового насоса.
Решение. Средняя наработка до отказа определяется по формуле
час.
Средний ресурс определяем по формуле
час.
Ответ. Средняя наработка до отказа равна час, данный показатель является:
— показателем безотказности;
— единичным, так как характеризует только одно свойств – безотказность;
— экспериментальным, так как определяется по результатам испытаний;
— смешанным, так как характеризует надежность небольшой партии изделий.
Средний ресурс равен , час, данный показатель является:
— показателем долговечности;
— единичным, так как характеризует только одно свойств – долговечность;
— экспериментальным, так как определяется по результатам испытаний;
— смешанным, так как характеризует надежность небольшой партии изделий.
Пример 3.2. На испытания поставлено 500 изделий. Результаты определения ресурса представлены в таблице 1.4. По данным испытаний определить гамма-процентный ресурс для γ = 95 %, 90 % и 80 %.
Таблица 3.1 – Результаты испытаний изделий
|
№№ |
Интервал времени, час |
Количество отказавших изделий n(t) |
|
1 |
0 – 100 |
24 |
|
2 |
100 – 200 |
29 |
|
3 |
200 – 300 |
35 |
|
4 |
300 – 400 |
15 |
|
5 |
400 – 500 |
16 |
|
6 |
500 – 600 |
20 |
|
7 |
600 – 700 |
35 |
|
8 |
700 – 800 |
57 |
|
9 |
800 – 900 |
133 |
|
10 |
900 – 1000 |
136 |
Решение. Для определения гамма-процентного ресурса необходимо найти значение наработки, вероятность которой равна 0,95; 0,90; 0,80, согласно формуле
.
Определим количество работоспособных изделий и вероятность безотказной работы на конец каждого временного интервала, результаты расчета сведены в таблицу 3.2.
Таблица 3.2 – Результаты расчета
|
№№ |
Интервал времени, час |
Количество отказавших изделий n(t) |
Количество работоспособных изделия N(t) к концу периода |
Вероятность безотказной работы P(t) |
|
1 |
0 – 100 |
24 |
476 |
0,952 |
|
2 |
100 – 200 |
29 |
447 |
0,894 |
|
3 |
200 – 300 |
35 |
412 |
0,824 |
|
4 |
300 – 400 |
15 |
397 |
0,794 |
|
5 |
400 – 500 |
16 |
381 |
0,762 |
|
6 |
500 – 600 |
20 |
361 |
0,722 |
|
7 |
600 – 700 |
35 |
326 |
0,652 |
|
8 |
700 – 800 |
57 |
269 |
0,538 |
|
9 |
800 – 900 |
133 |
136 |
0,272 |
|
10 |
900 – 1000 |
136 |
0 |
0 |
По представленному расчету вероятностям 0,95; 0,90 и 0,80 соответствуют значения наработки равные 100, 200 и 400 часов соответственно (выделены в таблице 3.2).
Ответ: гамма-процентные ресурсы равны Тр95 = 100 часов; Тр90 = 200 часов; Тр95 = 400 часов, показатели являются:
— показателем долговечности;
— единичным, так как характеризует только одно свойств – долговечность;
— экспериментальным, так как определяется по результатам испытаний;
— смешанным, так как характеризует надежность небольшой партии изделий.
Пример 3.3. В результате наблюдений за работой буровой лебедки получены следующие данные о времени, затраченном на смену тормозных лент, в часах: 2,5; 1,8; 1,8; 2,6; 0,8; 1,2; 0,6; 2,0; 1,6; 3.2. Всего 10 наблюдений. Определить среднее время восстановления буровой лебедки.
Решение: Статистическая оценка среднего времени восстановления вычисляется по формуле (1.13)
часа,
Ответ: среднее время восстановления равно часа, показатель является:
— показателем ремонтопригодности;
— единичным, так как характеризует только одно свойств – ремонтопригодность;
— эксплуатационным, так как определяется по результатам эксплуатации;
— единичным, так как характеризует надежность одного изделия.
Пример 3.4. Определить коэффициент готовности системы при среднем времени восстановления равном 2 часа и средней наработке на отказ равной 100 часов.
Решение: Среднее значение коэффициента готовности Кг вычисляют по формуле (1.16)
.
Ответ: Коэффициент готовности равен.
— показателем готовности;
— комплексным, так как характеризует безотказность, ремонтопригодность и готовность;
— эксплуатационным, так как определяется по результатам эксплуатации;
— единичным, так как характеризует надежность одного изделия.
Пример 3.5. Определить коэффициент технического использования, если известно, что система эксплуатируется в течение 1 года, годовой фонд времени системы составляет 8760 часов. Время проведения ежегодного техосмотра составляет 20 суток, суммарное время, затраченное на ремонтные работы, составляет 20 часов.
Решение: Коэффициент технического использования определяется по формуле (1.17)
.
Ответ: Коэффициент технического использования равен , показатель является:
— показателем готовности;
— комплексным, так как характеризует безотказность, ремонтопригодность и готовность;
— эксплуатационным, так как определяется по результатам эксплуатации;
— единичным, так как характеризует надежность одного изделия.
Задания для самостоятельной работы
Задача 3.1. На промысловые испытания поставлено 3 вертлюга. В ходе испытаний у первого насоса было зафиксировано 37 отказа, у второго – 29 отказов, у третьего – 48 отказов. Суммарная наработка на отказ для первого вертлюга составила 3100 часов, для второго – 2200 часов, для третьего – 2700 часов. Определить среднюю наработку до отказа.
Задача 3.2. На эксплуатацию поставлено 250 изделий. На моменты времени t1 – t7 зафиксировано определенное количество отказов (таблица 1.6). Остальные изделия не отказали. Определить средний ресурс.
Таблица 1.6.
|
ti, час |
50 |
100 |
150 |
200 |
250 |
300 |
350 |
|
n(ti) |
5 |
8 |
11 |
15 |
21 |
31 |
9 |
Задача 3.3. На промысловые испытания поставлено 3 насоса. В ходе испытаний у первого насоса было зафиксировано 37 отказа, у второго – 29 отказов, у третьего – 48 отказов. Суммарная наработка до отказа для первого насоса составила 3100 часов, для второго – 2200 часов, для третьего – 2700 часов. Определить средний ресурс насоса.
Задача 3.4. Длительность проведения технического обслуживания для бурового насоса составляет 45 часов. Межремонтный цикл составляет 2335 часов. Определить коэффициент готовности бурового насоса.
Задача 3.5. Какую длительность восстановления работоспособности должен иметь объект с межремонтным циклом 2000 часов, чтобы коэффициент готовности объекта составлял 0,95.
Задача 3.6. Определить среднее время восстановления компрессора, если на проведение 5 мелких ремонтов было затрачено 30,5 часа.
Задача 3.7. Годовое время работы одной буровой лебедки составляет 3500 часов. За год проводится 4 технических обслуживания продолжительностью 65 часов каждое и 1 средний ремонт продолжительностью 360 часов. Определить коэффициент технического использования буровой лебедки.
Задача 3.8. По данным задачи 3.7 определить коэффициент готовности буровой лебедки.
Задача 3.9. В ходе наблюдений за работой турбобура были зафиксированы отказы в следующие моменты времени: 110, 167, 284, 365, 512, 650 часов работы. Определить среднюю наработку между отказами турбобура.
Задача 3.10. По данным задачи 3.9 определить вероятность безотказной работы и вероятность отказа за 300 и 600 часов работы.
Контрольные вопросы:
- дайте определение средней наработки до отказа и средней наработки на отказ;
- какие показатели используются при определении долговечности;
- как определяются средний и гамма-процентный ресурс;
- как определяются средний и гамма-процентный срок службы,
- дайте характеристику показателям ремонтопригодности: вероятности восстановления, интенсивности восстановления, среднему сроку восстановления;
- дайте характеристику показателям сохраняемости: среднему сроку сохраняемости, гамма-процентному сроку сохраняемости;
- приведите определение и дайте характеристику коэффициенту готовности;
- приведите определение и дайте характеристику коэффициенту оперативной готовности;
- приведите определение и дайте характеристику коэффициенту технического использования;
- приведите определение и дайте характеристику коэффициенту сохранения эффективности.
Литература:
- Острейковский В.А. Теория надежности: учебник для вузов. – 2-е изд., испр. – М.: Высшая школа, 2008. – 464 с.
Подробнее о работе
- 1 страниц
- 2019 год
-
11
просмотров - 0 покупки
120 ₽
Работа будет доступна в твоём личном кабинете после покупки
Гарантия сервиса Автор24
Уникальность не ниже 50%
Среднее время безотказной работы изделия по статистическим данным оценивается выражением
, (2.5)
где ti — время безотказной работы i- го изделия; N- общее число изделий, поставленных на испытания; mt* — статистическая оценка среднего времени безотказной работы изделия.
Для определения mt* по формуле (2.5) необходимо знать моменты выхода из строя всех
Отсутствует
На испытание поставлено 10 однотипных изделий. Получены следующие значения ti (ti — время 6езотказной работы i- го изделия) : t1 =10* час; t2 = 19* час; t3 =12* час; t4 =13* час; t5 =16* час; t6 =14* час; t7 =15* час; t8 =11* час; t9 =17* час; t10 =18* час.
Определить статистическую оценку среднего времени mt* безотказной работы изделия.
Отсутствует
Форма заказа новой работы
Не подошла эта работа?
Закажи новую работу, сделанную по твоим требованиям
Среднее время безотказной работы изделия по статистическим данным оценивается выражением
, (2.5)
где ti — время безотказной работы i- го изделия; N- общее число изделий, поставленных на испытания; mt* — статистическая оценка среднего времени безотказной работы изделия.
Для определения mt* по формуле (2.5) необходимо знать моменты выхода из строя всех
Отсутствует
На испытание поставлено 10 однотипных изделий. Получены следующие значения ti (ti — время 6езотказной работы i- го изделия) : t1 =10* час; t2 = 19* час; t3 =12* час; t4 =13* час; t5 =16* час; t6 =14* час; t7 =15* час; t8 =11* час; t9 =17* час; t10 =18* час.
Определить статистическую оценку среднего времени mt* безотказной работы изделия.
Отсутствует
Купить эту работу
На испытание поставлено 10 однотипных изделий Получены следующие значения ti (ti время 6езотказной
120 ₽
или заказать новую
Лучшие эксперты сервиса ждут твоего задания
от 20 ₽
Гарантии Автор24
-
Гарантийный срок
10 дней с момента оплаты работы
-
Критерии обращения по гарантии
Работа не соответствует заявленному описанию или уникальность
менее
50% -
Куда обращаться
Оформить жалобу в личном кабинете
Инструкция
Ознакомиться с подробной инструкцией можно по
ссылке


Понравилась эта работа?
или
2 июля 2020 заказчик разместил работу
Выбранный эксперт:
| Купить эту работу vs Заказать новую | ||
|---|---|---|
|
0 раз |
Куплено | Выполняется индивидуально |
|
Не менее 40%
Исполнитель, загружая работу в «Банк готовых работ» подтверждает, что |
Уникальность | Выполняется индивидуально |
| Сразу в личном кабинете | Доступность | Срок 1—4 дня |
| 120 ₽ | Цена | от 20 ₽ |
Не подошла эта работа?
В нашей базе
27837 Решений задач
— поможем найти подходящую
5
Похожих
работ
Отзывы студентов
Решение задач
Решение задач
Решение задач
Решение задач