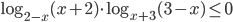На графике представлено изменение биржевой стоимости акций газодобывающей компании в первые две недели ноября. По горизонтали указываются числа месяца, по вертикали — стоимость акции в рублях. 2 ноября бизнесмен приобрел 10 акций этой компании. Шесть из них он продал 6 ноября, а 13 ноября — остальные 4. Известно, что цена акций убывала линейно. Сколько рублей потерял бизнесмен в результате этих операций?
Спрятать решение
Решение.
Стоимость акций 2 ноября составляла 2100 · 10 = 21 000 руб. Стоимость акций в течение шести дней с 3 по 9 ноября уменьшалась линейно, поэтому стоимость одной акции в третий день — 6 ноября — была равна полусумме стоимостей одной акции 3 и 9 ноября, то есть (2400 + 1500) : 2 = 1950 руб. за одну акцию. Следовательно, стоимость акций, проданных 6 ноября, была равна 1950 · 6 = 11 700 руб. Стоимость акций, проданных 13 ноября, равна 4 · 1200 = 4800 руб. Тем самым бизнесмен потратил 21 000 руб., а выручил 16 500 руб. Следовательно, убытки составили 4500 руб.
Ответ: 4500.
Примечание редакции Решу ЕГЭ.
Расчет стоимости акции является неотъемлемой частью решения. «Увидеть» точную стоимость непосредственно на графике в данной задаче нельзя. Полагаем, условие этой задачи, взятой нами из сборника для подготовки к ЕГЭ под редакцией И. В. Ященко, несколько превышает заложенную в ЕГЭ сложность заданий данного типа.
Условие
На графике, изображенном на рисунке, представлено изменение биржевой стоимости акций газодобывающей компании в первые две недели ноября. 2 ноября бизнесмен приобрел 10 акций этой компании. Шесть из них он продал 6 ноября, а 13 ноября — остальные 4. Сколько рублей потерял бизнесмен в результате этих операций?

математика 10-11 класс
14249
Решение
★
Вначале определим цену одного деления по горизонтали и по вертикали. По горизонтали — это дни: 1 деление — 1 день. По вертикали цена акции: т.к. 4 деления = 1200 руб., то 1 деление будет: 1200 : 4 = 300 руб.
Тогда 2 ноября цена одной акции была 2100 руб. Бизнесмен купил 10 акций и потратил 2100 · 10 = 21000 рублей.
6 ноября цена одной акции была 1950 руб. В этот день бизнесмен продал 6 акций и получил доход 1750 · 6 = 11700 руб.
13 ноября цена одной акции была 1200 руб. В этот день он продал остальные 4 акции и получил доход 1200 · 4 = 4800 руб.
Всего доход будет: 11700 + 4800 = 16500 руб.
Тогда в результате этих операций бизнесмен потерял 21000 — 16500 = 4500 рублей.
Написать комментарий
Задание 6266
На графике, изображенном на рисунке, представлено изменение биржевой стоимости акций газодобывающей компании в первые две недели ноября. 2 ноября бизнесмен приобрел 10 акций этой компании. Шесть из них он продал 6 ноября, а 13 ноября – остальные 4. Сколько рублей потерял бизнесмен в результате этих операций?
Ответ: 4500
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Приобрел за 2100, потратил 2100*10=21000 Продал 6 ноября за 1950, в 13 ноября за 1200 В итоге убыток составил: 21000-6*1950-4*1200=4500
ЕГЭ 2014 Типовой вариант 7
Условия задач с ответами и решениями
B1. Налог на доходы составляет 13% от заработной платы. Заработная плата Ивана Кузьмича равна 14500 рублей. Какую сумму он получит после вычета налога на доходы? Ответ дайте в рублях.
B2. На графике, изображенном на рисунке, представлено изменение биржевой стоимости акций газодобывающей компании в первые недели ноября. 2 ноября бизнесмен приобрел 10 акций этой компании. Шесть из них он продал 6 ноября, а 13 ноября — остальные 4. Сколько рублей потерял бизнесмен в результате этих операций?
B3. Найдите площадь трапеции АВСD.
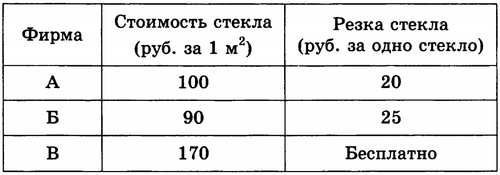
B4. Для изготовления книжных полок требуется заказать 40 одинаковых стекол в одной из трех фирм. Площадь каждого стекла равна 0,15 м2. В таблице приведены цены на стекло и на резку стекол. Сколько рублей нужно заплатить за самый выгодный заказ?
B5. Найдите корень уравнение
B6. Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 11, а одна из диагоналей ромба равна 44. Найдите величину тупого угла ромба. Ответ дайте в градусах.
B7. Вычислите значение выражения 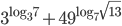
B8. На рисунке изображен график функции 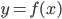
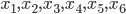
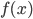
B9. Сторона основания правильной четырехугольной пирамиды вдвое больше ее высоты. Найдите угол между плоскостью боковой грани и плоскостью основания пирамиды. Ответ дайте в градусах.
B10. В магазине стоят два платежных автомата. Каждый из них может быть неисправен с вероятностью 0,06 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
B11. Объем данного правильного тетраэдра равен 2 см3. Найдите объем правильного тетраэдра, ребро которого в 3 раза больше ребра данного тетраэдра. Ответ дайте в см3.
B12. Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой 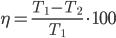
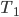
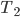
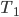
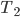
B13. Брюки дороже рубашки на 30% и дешевле пиджака на 22%. На сколько процентов рубашка дешевле пиджака?
B14. Найдите наибольшее значение функции 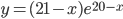
С1. а) Решите уравнение 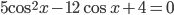
![[-5pi/2; -pi]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_031dcb2c8909a3fb709be751ca3600c0.gif)
С2. Основание прямой четырехугольной призмы ABCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = 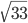
С3. Решите неравенство
С4. Треугольник ABC вписан в окружность радиуса 12. Известно, что АВ = 6 и ВС = 4. Найдите АС.
С5. Найдите все значения параметра 
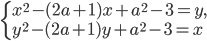
С6. Можно ли привести пример пяти различных натуральных чисел, произведение которых равно 792 и а) пять; б) четыре; в) три из них образуют геометрическую прогрессию?
Ответы
B1. 12615
B2. 4500
B3. 10,5
B4. 1020
B5. 1,5
B6. 120
B7. 20
B8. 2
B9. 45
B10. 0,9964
B11. 54
B12. 400
B13. 40
B14. 1
C1. а) 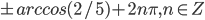
C2. 1,2
C3. (-2;-1]U(1;2)
C4.
C5. a=-2
C6. а) нет б) нет в) да
Буду рад даже если ответите хотябы на один вопрос.
1. Составить уравнение окислительно-восстановительных реакций протекающих по схеме
1)Zn +HNO3 —>Zn(^2+)+N2O+H2O
2)Zn+HNO3 —>Zn(^2+)+NO2+H2O
Уравнять электронно-ионным методом. Рассчитать ЭДС и сделать вывод о возможности самопроизвольного протекании реакции
2. Составить уравнение окислительно-восстановительных реакций протекающих по схемам
MnCl2+KOCl+KOH—>MnO2+KCl+H2O
Уравнять электронно-ионным методом. Рассчитать ЭДС и сделать вывод о возможности самопроизвольного протекании реакции
3. Написать молекулярные и сокращенные ионные уравнение реакций
CuSO4+Na2S—> CUSO4+NaOH—>K2S+HCl
Записать выражение ПР и К и их численные значение труднорастворимых веществ и слабых электролитов.
4. Составить уравнения окислительно-восстановительных реакций, протекающих по схемам:
1)Al +HNO3(разб.) —>Al3+ N2+H2O
2)Al+HNO3(конц.)—>Al^(3+)+NO2+H2O
Уравнять электронно-ионным способом. Рассчитать ЭДС и сделать вывод о возможности самопроизвольного протекании реакции
5. Рассчитать ЭДС гальванического элемента. Zn/ZnSO4//FeSO4/Fe
Указать анод и катод. Написать процессы на аноде и катоде. Условия стандартные.
6. Написать молекулярные и ионные уравнения гидролиза соли FeCl2. Как изменится характер среды?
7. С помощью молекулярных и ионных уравнений реакций раскрыть амфотерный характер гидроксида Sn(OH)2. К.ч. -4
8. Na2S+HOI —> S + NaI+NaOH
Уравнять электронно-ионным способом. Рассчитать ЭДС и сделать вывод о возможности самопроизвольного протекании реакций
9. Написать уравнение диссоциации H2PO4 и Fe(OH)3 по ступеням. Составить выражения констант диссоциации.
10. Составить уравнения окислительно-восстановительных реакций протекающих по схемам:
1)Zn +HNO3(разб.) —> Zn^(2+)+N2O+H2O
2) Zn+HNO3(конц.)—> Zn^(2+)+NO2+H2O
Уравнять электронно-ионным методом. Рассчитать ЭДС и сделать вывод о возможности самопроизвольного протекании реакций.
11. Составить уравнения окислительно-восстановительных реакций, протекающих по схемам:
KMnO4+H2SO4+Na2So3—> Mn2+…+… SO4^(2-)+…
Уравнять электронно-ионным методом. Рассчитать ЭДС и сделать вывод о возможности самопроизвольного протекании реакций.
12. Какие процессы протекают при электролизе IM раствора NiCl2? Электроды никелевые. Обосновать расчетом.
13. Написать молекулярные и ионные уравнения реакций:
1)Al(OH)3+HCl—>
2)Al(OH)3+NaOH—>к.ч. -4
14.Составить уравнения окислительно-восстановительных реакций, протекающих по схемам:
KMnO4+H2o+Na2SO3—>MnO2+…SO4^(2-)+…
Уравнять электронно-ионным методом. Рассчитать ЭДС и сделать вывод о возможности самопроизвольного протекании реакций.
15. Рассчитать потенциал электрода:
Zn/ZNSO4, 0,01M.
16. Составить уравнения окислительно-восстановительных реакций, протекающих по схемам:
Na2S+NaNO2+H2SO4—>S+NO+…
Уравнять электронно-ионным методом. Рассчитать ЭДС и сделать вывод о возможности самопроизвольного протекания реакций.
17. Рассчитать потенциал электрода:
Fe/Fe2+ , 0,0001 M.
18. Составить уравнения окислительно-восстановительных реакций, протекающих по схемам:
Al+NaOH+H2O—>H2+…
Уравнять электронно-ионным методом. Рассчитать ЭДС и сделать вывод о возможности самопроизвольного протекания реакций.
19. Какие процессы протекают при электролизе IM раствора ZaSO4. Электроды цинковые. Обосновать расчётом.
20. Написать молекулярные и ионно-молекулярные уравнения реакций.
1) ZnCL2+KOH(изб.)—>
21. Применяя уравнение Гиббса, определить термодинамическую возможность реакции: Nb2O3+5Ca=2Nb+5CaO
(K) (K) (K) (K)
при стандартных условиях.
22. С помощью молекулярных и ионных уравнений раскрыть амфотерный характер Pb(OH)2(^2).к.ч. =4
23. Составить уравнение окислительно-восстановительных реакций, протекающих по схемам:
1) Ni+HNO3 (разб.)—>
2) Ni+H2SO4(конц.)—>
3) Ni+HCl—>
Уравнять электронно-ионным методом. Рассчитать ЭДС и сделать вывод о возможности самопроизвольного протекания реакций.
24. Написать выражения констант диссоциации по ступеням для H2SO4 и Ca(OH)2.
25. Применяя уравнение Гиббса, рассчитать термодинамическую возможность реакции: 2CH4-C2H2+3H2
(Г) (Г) (Г)
при стандартных условиях.




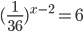

![[19; 21]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_b81641d8da7de295e0c61f7a1cee2d69.gif)