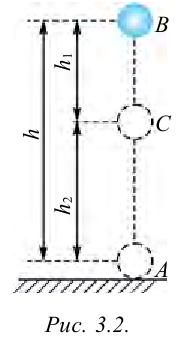
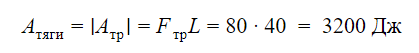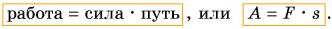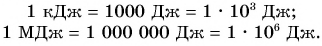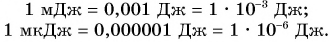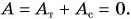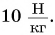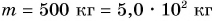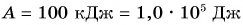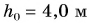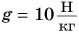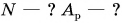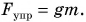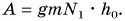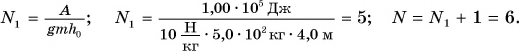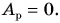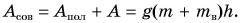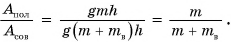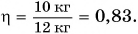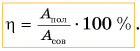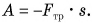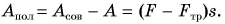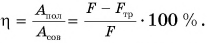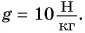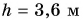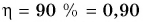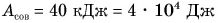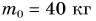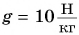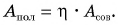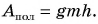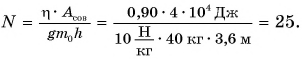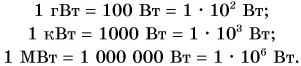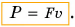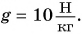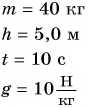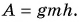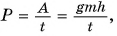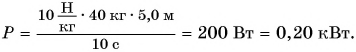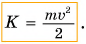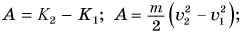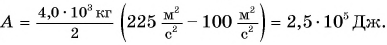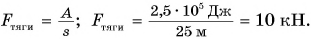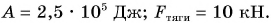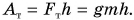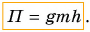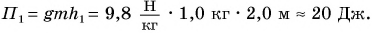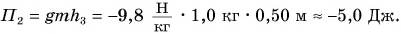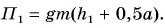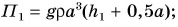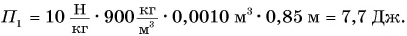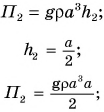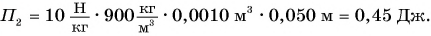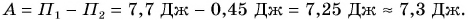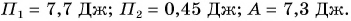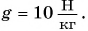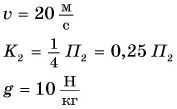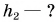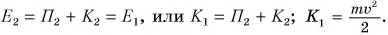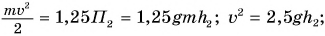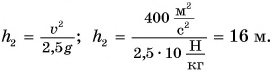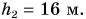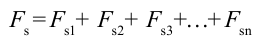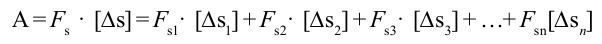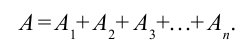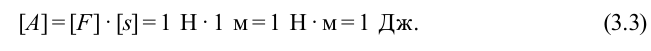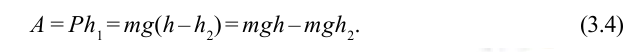Мощность.
Гипермаркет знаний>>Физика и астрономия>>Физика 10 класс>>Физика: Мощность
Очень часто важно знать не только работу, но и время, в течение которого она произведена. Поэтому надо ввести еще одну величину — мощность.
Работа может быть совершена как за большой промежуток времени, так и за очень малый. На практике, однако, далеко не безразлично, быстро или медленно может быть произведена работа. Временем, в течение которого совершается работа, определяют производительность любого двигателя. Очень большую работу может совершить и крошечный электромоторчик, но для этого понадобится много времени. Потому наряду с работой вводят величину, характеризующую быстроту, с которой она производится, — мощность.
Мощностью называют отношение работы A к интервалу времени , за который эта работа совершена:
Иными словами, мощность численно равна работе, совершенной в единицу времени.
Подставляя в формулу (6.4) вместо работы A ее выражение (6.2), получим
Таким образом, мощность равна произведению модуля вектора силы на модуль вектора скорости и на косинус угла между направлениями этих векторов.
Понятие мощности вводится для оценки работы за единицу времени, совершаемой каким-либо механизмом (насосом, подъемным краном, мотором машины и т. д.). Поэтому в формулах (6.4) и (6.5) под всегда подразумевается сила тяги.
В СИ мощность выражается в ваттах (Вт). Мощность равна 1 Вт, если работа 1 Дж совершается за 1 с.
Наряду с ваттом используются более крупные (кратные) единицы мощности:
1 гВт (гектоватт) = 100 Вт,
1 кВт (киловатт) = 1000 Вт,
1 МВт (мегаватт) = 1 000 000 Вт.
Мощность можно повысить как за счет увеличения действующих сил, так и за счет увеличения скорости движения.
Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс
Планирования по физике, учебники и книги онлайн, курсы и задания по физике для 10 класса
Содержание урокаконспект урока
опорный каркас
презентация урока
акселеративные методы
интерактивные технологии Практика
задачи и упражнения
самопроверка
практикумы, тренинги, кейсы, квесты
домашние задания
дискуссионные вопросы
риторические вопросы от учеников Иллюстрации
аудио-, видеоклипы и мультимедиа
фотографии, картинки
графики, таблицы, схемы
юмор, анекдоты, приколы, комиксы
притчи, поговорки, кроссворды, цитаты Дополнения
рефераты
статьи
фишки для любознательных
шпаргалки
учебники основные и дополнительные
словарь терминов
прочие Совершенствование учебников и уроков
исправление ошибок в учебнике
обновление фрагмента в учебнике
элементы новаторства на уроке
замена устаревших знаний новыми Только для учителей
идеальные уроки
календарный план на год
методические рекомендации
программы
обсуждения Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний — Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов —
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других «взрослых» тем.
Разработка — Гипермаркет знаний 2008-
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: 
Физика, 10 класс
Урок 13. Работа. Мощность. Энергия. Закон сохранения механической энергии
Перечень вопросов, рассматриваемых на уроке:
1. Работа
2. Мощность
3. Механическая энергия
4. Закон сохранения механической энергии.
Глоссарий по теме
Работа постоянной силы равна произведению модулей силы и перемещения точки приложения силы и косинуса угла между ними.
Мощность – отношение работы к интервалу времени, за который эта работа совершена.
Кинетическая энергия– энергия, которой обладает движущееся тело.
Кинетическая энергия материальной точки – величина равная половине произведения массы материальной точки на квадрат её скорости.
Теорема об изменении кинетической энергии: изменение кинетической энергии материальной точки при её перемещении равно работе, совершённой силой, действующей на точку при этом перемещении.
Если на точку действуют несколько сил, то изменение её кинетической энергии равно алгебраической сумме работ всех сил, действующих на неё.
Работа силы тяжести зависит только от положений начальной и конечной точек траектории и не зависит от формы траектории. При движении тела по замкнутой траектории работа силы тяжести равна нулю.
Консервативными силами называют силы, работа которых не зависит от формы траектории точки приложения силы и по замкнутой траектории равна нулю.
Работа силы упругости при растяжении пружины, т.е. когда направление силы противоположно перемещению тела, меньше нуля. Если начальное и конечное состояния пружины совпадают, то суммарная работа силы упругости при деформации пружины равна нулю.
Потенциальной энергией тела в поле силы тяжести называют величину, равную произведению массы тела на ускорение свободного падения и на высоту тела над поверхностью Земли.
Потенциальной энергией упругодеформированного тела называют величину, равную половине произведения коэффициента упругости тела на квадрат удлинения или сжатия.
Потенциальная энергия – энергия взаимодействия тел, обусловленная их взаимным расположением или взаимным расположением частей тела.
Полная механическая энергия равна сумме кинетической и потенциальной энергий тел, входящих в систему.
Закон сохранения энергии – энергия не создаётся и не уничтожается, а только превращается из одной формы в другую.
Основная и дополнительная литература по теме урока
Мякишев Г.Я., Буховцев Б.Б, Сотский Н.Н. Физика. 10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. С. 131-147.
Рымкевич А.П. Сборник задач по физике. 10-11 класс.-М.:Дрофа,2009. С.49-56.
ЕГЭ 2017. Физика. 1000 задач с ответами и решениями. Демидова М.Ю., Грибов В.А., Гиголо А.И. М.: Экзамен, 2017.
Теоретический материал для самостоятельного изучения
Влияние на тело сил, приводящее к изменению модуля их скорости, характеризуется величиной, которая зависит как от сил, так и от перемещения тел. Эта величина в механике называется работой силы, определяется по формуле:
Эта формула справедлива в случае, когда проекция силы на смещение постоянна.
Если есть угол между силой и смещением, то проекция силы равна произведению силы на косинус этого угла.
В этом случае работа постоянной силы равна произведению модулей силы и смещения точки приложения силы и косинуса угла между ними.
Работа по сравнению с силой и смещением — это не вектор, а скалярная величина. Она может быть, отрицательной равной нулю или положительной. Таким образом, знак работы определяется знаком косинуса угла между силой и перемещением.
Если сила F перпендикулярна перемещению тела, то работа, этой силой равна нулю. Это тот случай, когда действует сила, но тело не двигается.
Если на тело действует несколько сил, проекция результирующей силы на перемещение равна сумме проекций отдельных сил.
Fr = F1r+F2r+…
Поэтому суммарная работа, (алгебраическая сумма работ всех сил), равна работе результирующей силы.
В жизни важно те только совершение работы, но и время, за которое выполняется работа. Работу мы можем делать быстро и медленно. Отношение работы к временному интервалу, за который выполняется эта работа называется мощностью.
Как вы думаете, что необходимо для движения тела? Да, энергия необходима. Энергия характеризует способность тела (или системы тел) совершать работу. Кинетическая энергия – энергия, которой обладает движущееся тело
И энергия может быть кинетической и потенциальной.
Кинетическая энергия материальной точки равна половине массы материальной точки на квадрат её скорости:
Теорема об изменении кинетической энергии: изменение кинетической энергии материальной точки при её перемещении равно работе силы, действующей на точку во время этого перемещении.
Работа силы тяжести не зависит от формы траектории, а зависит только от положений начальной и конечной точек траектории
А = mgh1 – mgh2.
При движении тела по замкнутой траектории работа силы тяжести равна нулю.
Силы, работа которых не зависит от формы траектории точки приложения силы и на замкнутой траектории равна нулю, называют консервативными силами.
Работа при растяжении пружины силы упругости, когда направление силы совпадает с направлением движения тела, принимает положительные значения и определяется по формуле: 
В случае при увеличении деформации пружины, когда сила упругости, действующая на тело со стороны пружины, направлена противоположно деформации, работа силы упругости отрицательна:

Согласно теореме, об изменении кинетической энергии ΔЕк = Ек2 – Ек1 работа силы, действующей на тело, равна изменению его кинетической энергии:

Если силы взаимодействия между телами консервативны, то работу сил можно представить, как разность двух значений некоторой величины, зависящей от взаимного расположения тел или частей одного тела: А = mgh1 – mgh2, работы силы тяжести

и работы силы упругости.
Величина, равная произведению массы m тела на ускорение свободного падения g и высоту h тела над поверхностью Земли, называется потенциальной энергией тела в поле силы тяжести.
Закон сохранения механической энергии:
В изолированной системе, в которой действуют консервативные силы, механическая энергия сохраняется.
Е = Ек + Еп = const

Закон сохранения механической энергии является частным случаем общего закона сохранения энергии: энергия не создаётся и не разрушается, а преобразуется из одной формы в другую.
Примеры и разбор решения заданий
1.
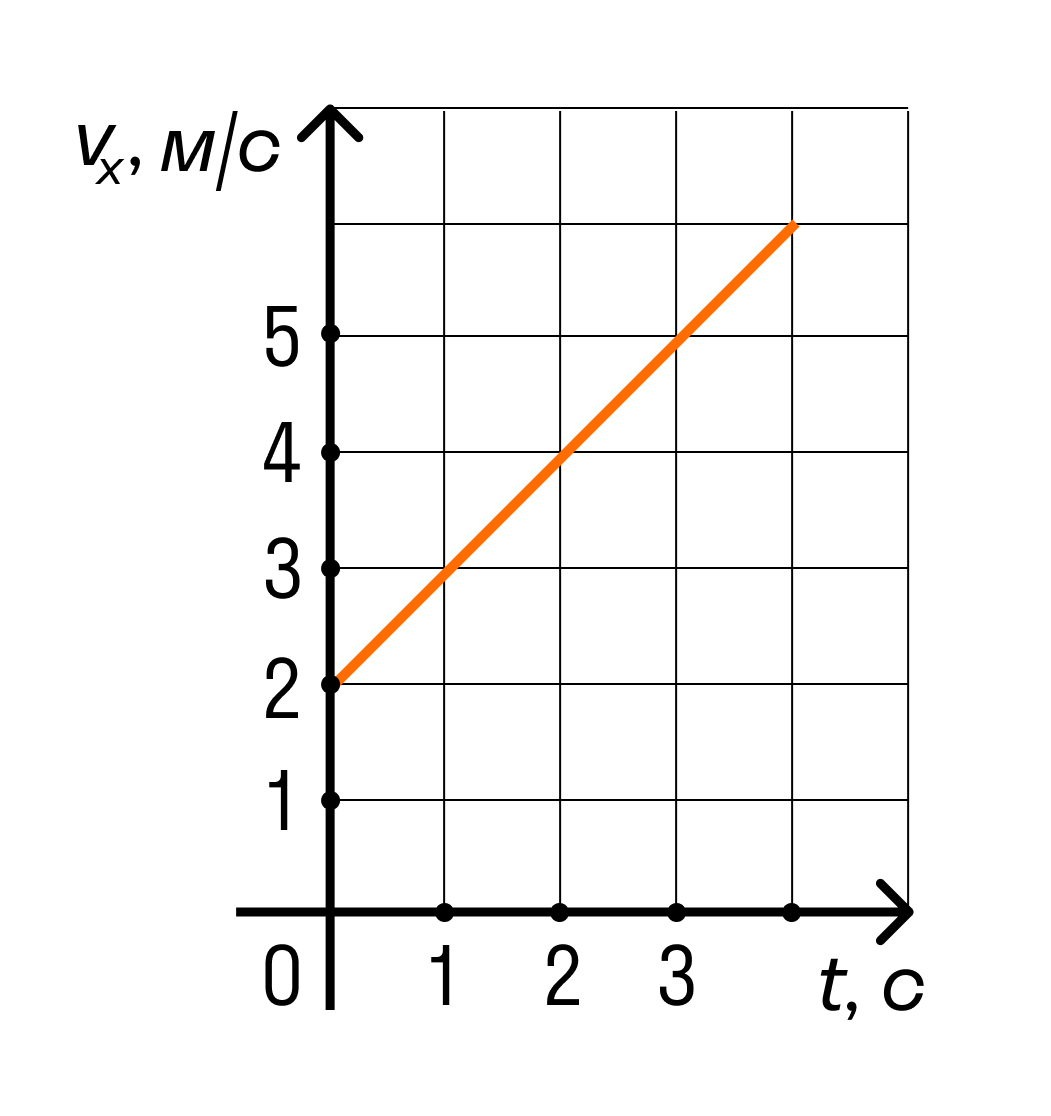
Тело движется вдоль оси ОХ под действием силы F = 2 Н, направленной вдоль этой оси. На рисунке приведён график зависимости проекции скорости vх тела на эту ось от времени t. Какую мощность развивает эта сила в момент времени t = 3 с?
Решение: по графику проекция скорости в момент времени 3с, равна 5 м/с. Мощность, развиваемая силой F для тела, движущегося со скоростью можно найти по формуле

Ответ: 10 Вт
2. Троллейбус массой 15 т трогается с места с ускорением 1,4 м/с2. Найти работу силы тяги и работу силы сопротивления на первых 10 м пути, если коэффициент сопротивления равен 0,05. Каково изменение кинетической энергии автобуса?
Дано:
m = 15т = 15 ·103кг
S = 10м
а = 1,4 м/с2
µ = 0,05
Найти: Ат; Ас; Ек
Запишем уравнение второго закона Ньютона:

в проекции на ось ОХ:
ma = Fт – Fтр
Fтр = µmg → Fт = ma + µmg = m(a+ µg);
По определению работы:
Ат = Fт S = m(a+ µg)S ;
Aт = 15 ·103 кг (1,4 м/с2+0,05 ·10 м/с2) ·10 м = 285 кДж
Работа силы сопротивления: Ас = -FтрS = — µmgS
Ас = -0,05·15·103 кг·10 м/с2·10м = -75 кДж
Кинетическая энергия определяется по формуле:
Ек = mv2/2. Скорость определим по формуле:

Ек = 15·103 кг·14 м/с2 = 210 кДж
Ответ: Ат = 285 кДж; Ас = -75 кДж; Ек = 210 кДж.
Для нас привычно понятие «работа» в бытовом смысле. Работая, мы совершаем какое-либо действие, чаще всего полезное. В физике (если точнее, то в механике) термин «работа» показывает, какую силу в результате действия приложили, и на какое расстояние тело в результате действия этой силы переместилось.
Например, нам нужно поднять велосипед по лестнице в квартиру. Тогда работа будет определяться тем, сколько весит велосипед и на каком этаже (на какой высоте) находится квартира.
Механическая работа — это физическая величина, прямо пропорциональная приложенной к телу силе и пройденному телом пути.
Чтобы рассчитать работу, нам необходимо умножить численное значение приложенной к телу силы F на путь, пройденный телом в направлении действия силы S. Работа обозначается латинской буквой А.
Механическая работа
А = FS
A — механическая работа [Дж]
F — приложенная сила [Н]
S — путь [м]
Если под действием силы в 1 ньютон тело переместилось на 1 метр, то данной силой совершена работа в 1 джоуль.
Поскольку сила и путь — векторные величины, в случае наличия между ними угла формула принимает вид.
Механическая работа
А = FScosα
A — механическая работа [Дж]
F — приложенная сила [Н]
S — путь [м]
α — угол между векторами силы и перемещения [°]
Числовое значение работы может становиться отрицательным, если вектор силы противоположен вектору скорости. Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае сила называется противодействующей.
Для совершения работы необходимы два условия:
- чтобы на тело действовала сила,
- чтобы происходило перемещение тела.
Сила, действующая на тело, может и не совершать работу. Например, если кто-то безуспешно пытается сдвинуть с места тяжелый шкаф. Сила, с которой человек действует на шкаф, не совершает работу, поскольку перемещение шкафа равно нулю.
Запомнить!
Работа равна нулю, если:
- при приложенной силе перемещение отсутствует;
- сила не приложена и тело перемещается по инерции;
- угол между векторами силы и перемещения равен 90°.
Полезная и затраченная работа
Был такой мифологический персонаж у древних греков — Сизиф. За то, что он обманул богов, те приговорили его после смерти вечно таскать огромный булыжник вверх по горе, откуда этот булыжник скатывался — и так без конца. В общем, Сизиф делал совершенно бесполезное дело с нулевым КПД. Поэтому бесполезную работу и называют «сизифов труд».
Чтобы разобраться в понятиях полезной и затраченной работы, давайте пофантазируем и представим, что Сизифа помиловали и камень больше не скатывается с горы, а КПД перестал быть нулевым.
Полезная работа в этом случае равна потенциальной энергии, приобретенной булыжником. Потенциальная энергия, в свою очередь, прямо пропорциональна высоте: чем выше расположено тело, тем больше его потенциальная энергия. Выходит, чем выше Сизиф прикатил камень, тем больше полезная работа.
Потенциальная энергия
Еп = mgh
m — масса тела [кг]
g — ускорение свободного падения [м/с2]
h — высота [м]
На планете Земля g ≈ 9,8 м/с2
Затраченная работа в нашем примере — это механическая работа Сизифа. Механическая работа зависит от приложенной силы и пути, на протяжении которого эта сила была приложена.
Механическая работа
А = FS
A — механическая работа [Дж]
F — приложенная сила [Н]
S — путь [м]
И как же достоверно определить, какая работа полезная, а какая затраченная?
Все очень просто! Задаем два вопроса:
-
За счет чего происходит процесс?
-
Ради какого результата?
В примере выше процесс происходит ради того, чтобы тело поднялось на какую-то высоту, а значит — приобрело потенциальную энергию (для физики это синонимы).
Происходит процесс за счет энергии, затраченной Сизифом — вот и затраченная работа.
Мощность
На заводах по всему миру большинство задач выполняют машины. Например, если нам нужно закрыть крышечками тысячу банок колы, аппарат сделает это в считанные минуты. У человека эта задача заняла бы намного больше времени. Получается, что машина и человек выполняют одинаковую работу за разные промежутки времени. Для того, чтобы описать скорость выполнения работы, нам потребуется понятие мощности.
Мощностью называется физическая величина, равная отношению работы ко времени ее выполнения.
Мощность
N = A/t
N — мощность [Вт]
A — механическая работа [Дж]
t — время [с]
Один ватт — это мощность, при которой работа в один джоуль совершается за одну секунду.
Также для мощности справедлива другая формула:
Мощность
N = Fv
N — мощность [Вт]
F — приложенная сила [Н]
v — скорость [м/с]
Как и для работы, для мощности справедливо правило знаков: если векторы направлены противоположно, значение мощности будет отрицательным.
Поскольку сила и скорость — векторные величины, в случае наличия между ними угла формула принимает следующий вид:
Мощность
N = Fvcosα
N — мощность [Вт]
F — приложенная сила [Н]
v — скорость [м/с]
α — угол между векторами силы и скорости [°]
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Пятерка по физике у тебя в кармане!
Решай домашку по физике на изи. Подробные решения помогут разобраться в сложной теме и получить пятерку!
Примеры решения задач
Задача 1
Ложка медленно тонет в большой банке меда. На нее действуют сила тяжести, сила вязкого трения и выталкивающая сила. Какая из этих сил при движении тела совершает положительную работу? Выберите правильный ответ:
-
Выталкивающая сила.
-
Сила вязкого трения.
-
Сила тяжести.
-
Ни одна из перечисленных сил.
Решение
Поскольку ложка падает вниз, перемещение направлено вниз. В ту же сторону, что и перемещение, направлена только сила тяжести. Это значит, что она совершает положительную работу.
Ответ: 3.
Задача 2
Ящик тянут по земле за веревку по горизонтальной окружности длиной L = 40 м с постоянной по модулю скоростью. Модуль силы трения, действующей на ящик со стороны земли, равен 80 H. Чему равна работа силы тяги за один оборот?
Решение
Поскольку ящик тянут с постоянной по модулю скоростью, его кинетическая энергия не меняется. Вся энергия, которая расходуется на работу силы трения, должна поступать в систему за счет работы силы тяги. Отсюда находим работу силы тяги за один оборот:
Ответ: 3200 Дж.
Задача 3
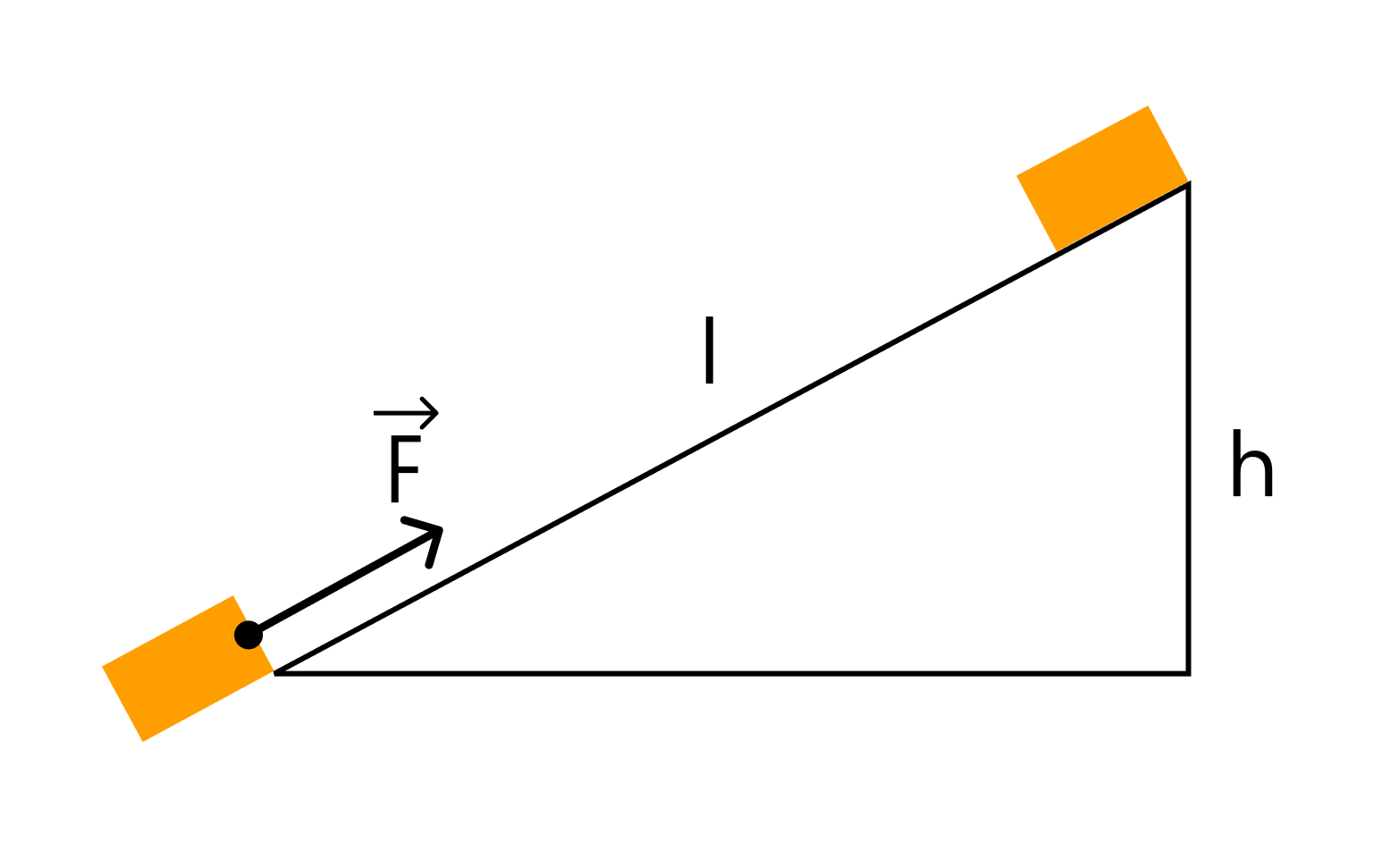
Тело массой 2 кг под действием силы F перемещается вверх по наклонной плоскости на расстояние l = 5 м. Расстояние тела от поверхности Земли при этом увеличивается на 3 метра. Вектор силы F направлен параллельно наклонной плоскости, модуль силы F равен 30 Н. Какую работу при этом перемещении в системе отсчета, связанной с наклонной плоскостью, совершила сила F?
Решение
В данном случае нас просят найти работу силы F, совершенную при перемещении тела по наклонной плоскости. Это значит, что нас интересуют сила F и пройденный путь. Если бы нас спрашивали про работу силы тяжести, мы бы считали через силу тяжести и высоту.
Работа силы определяется как скалярное произведение вектора силы и вектора перемещения тела. Следовательно:
A = Fl = 30 * 5 = 150 Дж
Ответ: 150 Дж.
Задача 4
Тело движется вдоль оси ОХ под действием силы F = 2 Н, направленной вдоль этой оси. На рисунке приведен график зависимости проекции скорости vx тела на эту ось от времени t. Какую мощность развивает эта сила в момент времени t = 3 с?
Решение
На графике видно, что проекция скорости тела в момент времени 3 секунды равна 5 м/с.
Мощность можно найти по формуле N = Fv.
N = FV = 2×5 = 10 Вт
Ответ: 10 Вт.
Попробуйте онлайн-курс подготовки к ЕГЭ по физике с опытным преподавателем в Skysmart!
Содержание:
Работа, мощность и энергия:
Мы часто слышим от друзей: «Я сегодня выполнил большую работу: выучил наизусть стихотворение и решил пять задач по математике». Но с точки зрения физики никакой работы не совершено, даже если выучить наизусть целую поэму. Что же такое работа в физике?
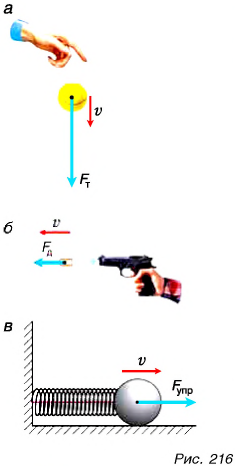
В физике работа оценивает то, что вызвала сила, действуя на движущееся тело. Покажем это на примерах. Рассмотрите внимательно рисунок 216. Что общего в результатах действия силы тяжести на мяч (рис. 216, а), силы давления газа на пулю в пистолете (рис. 216, б) и силы упругости сжатой пружины на шарик (рис. 216, в) после пережигания нити? Все перечисленные силы вызывают разгон тел (мяча, пули, шарика), т. е. увеличение скорости движения.
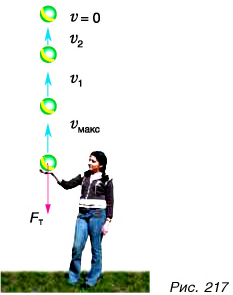
Л может ли сила, действующая на движущееся тело, уменьшать его скорость? Подбросьте мяч и наблюдайте за его движением вверх (рис. 217). Теперь сила тяжести уменьшает скорость его движения. Во всех случаях, когда сила изменяет скорость движения (увеличивает или уменьшает), говорят, что сила совершает механическую работу.
Механическая работа является физической величиной. Ее значение можно рассчитать. Рассмотрим самый простой случай: направление силы совпадает с направлением движения. Например, идет разгон спортивных саней (рис. 218). Изменение скорости саней, а значит, и работа по их разгону зависят от значения действующей силы (силы спортсменов, разгоняющих сани) и от пройденного санями пути. Чем больше сила и путь, тем большая совершается работа. Этот вывод справедлив для всех движущихся под действием силы тел.
Таким образом, механическая работа — физическая величина, пропорциональная действующей на тело силе и пройденному пути.
Обозначим работу буквой А. Тогда, если направление силы совпадает с направлением движения тела,
Единицей работы в СИ является 1 джоуль (1 Дж). Названа она в честь известного английского физика Дж. П. Джоуля. Один джоуль — это работа, совершаемая силой 1 Н на пути 1 м.
1 джоуль = 1 ньютон • 1 метр.
Для измерения большой работы используют кратные джоулю единицы:
В случае малой работы применяются дольные единицы:
Из формулы работы следует, что если есть силы, но нет движения, то нет и работы. Например, сила тяжести, действующая на лежащий на столе мяч (рис. 219, а), работы не совершает, а в случае падающего мяча (рис. 219, б) — совершает.
Сила не всегда увеличивает скорость движения тела. Так, при движении мяча вверх (см. рис. 217) сила тяжести замедляет его движение. Аналогично при скольжении шайбы по льду сила трения уменьшает скорость движения шайбы. Работу силы (тяжести, трения) в подобных случаях считают отрицательной.
Но положительная и отрицательная работы могут совершаться одновременно и даже быть равными по абсолютной величине. В этом случае скорость движения постоянна. Например, электропоезд на данном участке пути движется равномерно. Это значит, что равнодействующая сил (тяги двигателя и сопротивления движению) равна нулю. По и сила тяги, и сила сопротивления совершают работу. Только работа силы тяги 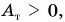
Главные выводы:
- Механическая работа характеризует результат действия силы на движущееся тело и пропорциональна действующей на тело силе и пройденному телом пути.
- Силы, ускоряющие движение тела; совершают положительную работу.
- Силы, замедляющие движение тела, совершают отрицательную работу.
- Единица работы в СИ — 1 джоуль (1 Дж).
Пример решения задачи:
Подъемный кран равномерно поднимает с земли бетонную плиту массой m = 500 кг на один из этажей строящегося дома. Сила упругости троса при этом совершает работу А = 100 кДж. Определите, на какой этаж была поднята плита, если высота одного этажа 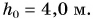
Дано:
Решение:
При равномерном подъеме сила упругости троса равна силе тяжести, действующей на плиту:
Работа силы упругости 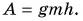
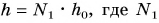
Отсюда
Так как движение плиты равномерное, то равнодействующая сил, приложенных к ней, 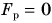
Ответ: плита поднята на 6-й этаж; работа равнодействующей сил
Полезная и совершённая работа
Оценивая работу машины, механизма и др., говорят об их коэффициенте полезного действия (КПД). Но что такое КПД? Что означают слова «полезного действия»? А что такое неполезное действие?
Рассмотрим ситуацию: идет уборка картофеля на поле. Фермер поднимает картофель в ведре в кузов автомашины (рис. 221), выгружает, а ведро опускает на землю. Механическую работу совершает мускульная сила фермера, поднявшего ведро массой, например, 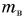
Цель фермера — погрузить в кузов картофель. Исходя из этого, полезной работой является работа по подъему картофеля: 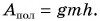
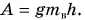
Какую долю составляет полезная работа от совершенной?
Обозначим отношение 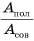
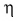
КПД, как правило, выражают в процентах.
Таким образом, КПД (эффективность работы) в данном случае равен 83 %.
Рассмотрим еще один пример. Дети разгоняют санки, действуя силой F в направлении их движения (рис. 222). Совершенная (полная) работа здесь 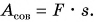
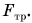
Полезной же работой была
Тогда доля полезной работы (КПД)
Физическая величина, равная отношению полезной работы к совершенной (полной), называется коэффициентом полезного действия.
А могут ли механизм, машина, человек работать так, чтобы КПД = 100 %, т. е. чтобы вся совершенная работа была полезной?
Ученые неоднократно пытались создать такую машину (рис. 223), но все попытки оказались безуспешными. (Самостоятельно познакомьтесь в Интернете или справочной литературе с информацией о вечном двигателе.) В работе любой машины, механизма всегда есть неполезная работа, идущая на преодоление трения, сопротивления. А значит, КПД всегда меньше 100 %. А вот сделать неполезную работу минимальной означает повысить КПД.
Главные выводы:
- Совершенная (т. е. полная) механическая работа всегда больше полезной.
- КПД показывает, какую долю составляет полезная работа от всей совершенной.
- Чем больше полезная работа, тем выше КПД.
- КПД всегда меньше 100 %.
Пример решения задачи:
При подъеме картофеля из хранилища глубиной h = 3,6 м подъемным устройством с КПД 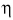
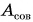
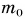
Дано:
Решение:
Зная совершенную работу и КПД, можно найти полезную работу по подъему мешков картофеля:
Полезная работа — это работа подъемного устройства по преодолению силы тяжести, действующей на картофель:
Масса 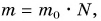
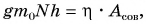
Ответ: N = 25 мешков.
Мощность и единицы мощности
Приобретая автомобиль (рис. 226), газонокосилку, микроволновую печь (рис. 227) и др., человек интересуется их мощностью. Именно мощность является паспортной характеристикой машин и механизмов. Что же такое мощность? Почему так важно ее знать?
Рассмотрим пример. Человек лопатой копает яму для погреба в течение нескольких дней. Такую же яму экскаватор (рис. 228) выкопает за несколько минут. Работа выполняется одинаковая. Одинаковая масса грунта поднимается на одну и ту же высоту. Но быстрота совершения работы человеком и экскаватором разная. За единицу времени экскаватор выполняет во много раз большую работу, чем человек. Для описания быстроты совершения работы вводится мощность.
Физическая величина, равная отношению работы к промежутку времени, за который эта работа совершена, называется мощностью. Обозначается мощность буквой Р.
За единицу мощности в СИ принимается мощность, при которой действующая на тело сила за время t = 1 с совершает работу А = 1 Дж. Эта единица мощности называется ватт (Вт) в честь английского изобретателя Дж. Уатта. Для измерения больших мощностей используют кратные единицы: гектоватт (гВт), киловатт (кВт), мегаватт (МВт). Обратите внимание:
Для малых мощностей употребляются дольные единицы — милливатт (мВт), микроватт (мкВт):
В быту часто необдуманно единицу мощности киловатт принимают за единицу работы. Но работа 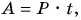
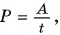
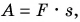
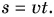
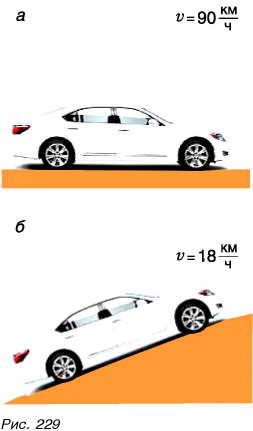
Мощность пропорциональна силе, совершающей работу, и скорости движения. Тогда при постоянной мощности чем меньше скорость, тем больше сила. Вот почему водитель, трогаясь с места или поднимаясь в гору (рис. 229), когда требуется большая сила, едет на малой скорости. Тем самым он увеличивает силу тяги двигателя автомобиля.
Главные выводы
- Мощность — физическая величина, характеризующая быстроту совершения работы.
- Единицей мощности в СИ является 1 ватт.
- Одинаковую мощность можно получить либо при большой скорости и небольшой силе, либо при малой скорости и большой силе.
Для любознательных
В автомобилестроении по традиции используют старинную единицу мощности — лошадиную силу (л. с.). С помощью рисунка сформулируйте самостоятельно определение мощности в 1 лошадиную силу.
Запишем связь 1 л. с. и ватта: 1 л. с. = 736 Вт.
В этих внесистемных единицах мощность первого белорусского трактора МТЗ-2 (1953 г.) была равна 37 л. с. Освоенный в 2010 г. трактор «Беларус-3023» имеет двигатель мощностью 300 л. с. Переведите эти знамения мощности в единицы СИ самостоятельно и сравните их.
Пример решения задачи:
На уроке физкультуры мальчик массой m = 40 кг поднялся по канату на высоту h = 5,0 м за промежуток времени t = 10 с. Определите среднюю мощность, развиваемую мальчиком при подъеме. Коэффициент
Дано:
Решение:
При подъеме по канату работа мускульной силы рук идет на преодоление силы тяжести.
Тогда
Ответ: P = 0, 20 кВт.
Кинетическая энергия
Энергия — одно из наиболее важных и сложных понятий. Причем не только в физике, но и в других науках. А что же такое кинетическая энергия?
Рассмотрим два примера. Шайба, попадая в сетку ворот (рис. 230), прогибает ее. Молот для забивания свай (рис. 231), падая на сваю, загоняет ее в землю на некоторую глубину. Чтобы сильнее прогнуть сетку или глубже забить сваю, шайба и молот должны иметь большую скорость. И шайба, и молот совершили работу. При этом скорость их движения изменилась (уменьшилась до нуля). Совершенные ими работы были разными, даже если предположить, что скорости движения были одинаковыми. Но массы молота и шайбы не равны.
Если тело способно совершить работу, то оно обладает энергией. В физике энергию движущегося тела называют кинетической (от греч. kinetikos — приводящий в движение). Кинетическая энергия обозначается буквой К (или 
Большая кинетическая энергия движущихся тел — камня, автомобиля, железнодорожного состава (рис. 232), метеорита и др. — означает, во-первых, что при разгоне их до данной скорости разгоняющей силой была совершена большая работа и, во-вторых, при их остановке тормозящей силой будет совершена такая же большая работа.
Из примеров следует, что кинетическая энергия зависит от массы тела и скорости его движения. Какой является эта зависимость?
Опыты показывают, что кинетическая энергия прямо пропорциональна массе тела и квадрату скорости его движения:
Увеличение скорости движения тела, например в 4 раза, приводит к возрастанию кинети- Обратите внимание! ческой энергии в 16 раз. Об этом должны всегда помнить водители и пешеходы.
Главные выводы:
- Кинетическая энергия выражает способность движущихся тел совершать работу.
- Кинетическая энергия, как и работа, измеряется в джоулях.
- Кинетическая энергия тела зависит от его массы и скорости.
- Изменить (увеличить или уменьшить) кинетическую энергию тела можно только путем совершения работы (положительной или отрицательной).
Пример решения задачи:
Скорость движения груженого автомобиля массой m = 4,0 т увеличилась от 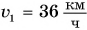
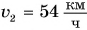
Дано:
Решение:
Чтобы увеличить кинетическую энергию от 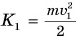
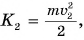
Но работа 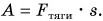
Ответ:
Потенциальная энергия
При разгоне любого тела (санок, автомобиля и др.) у него возникает способность совершить механическую работу — у движущегося тела появляется кинетическая энергия. А если тело неподвижно? Обладает ли оно способностью совершить работу?
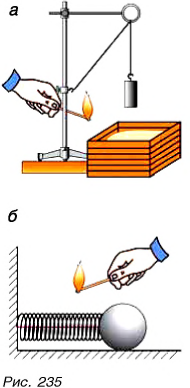
Проведем два опыта. В первом поднимем и укрепим на нити над ящиком с песком гирю (рис. 235, а). Во втором между упором и шариком поместим предварительно сжатую и связанную ниткой пружину (рис. 235, б). Оба тела (гиря и пружина) неподвижны 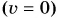
Важно понимать, что потенциальная энергия не появляется сама по себе. В этих опытах гиря была поднята над столом, пружина была сжата какой-то силой. Значит, чтобы тело запасло потенциальную энергию, необходимо совершить работу. Чем сильнее будет сжата пружина, чем выше будет поднято тело, тем больше у них будет запас потенциальной энергии. Тела, представленные на рисунке 236, уже обладают потенциальной энергией. У трамплина она вызвана прогибом (деформацией) доски, у мышеловки — закручиванием пружины, у лука — изменением расположения древка и тетивы. Из этих и других примеров следует, что потенциальная энергия — это энергия, обусловленная взаимным расположением взаимодействующих тел или частей тела (гири и Земли, стрелы и тетивы, звеньев пружины). Обозначается потенциальная энергия буквой П (или 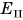
Именно благодаря потенциальной энергии сжатой (закрученной) пружины работают механические часы, реле времени микроволновых печей, стиральных машин, движутся некоторые детские игрушки. Потенциальная энергия поднятой с помощью плотины воды заставляет работать гидроэлектростанции (рис. 237).
Главные выводы:
- Неподвижные взаимодействующие тела (система тел) могут обладать способностью совершать механическую работу, а значит, потенциальной энергией.
- Значение потенциальной энергии зависит от взаимного расположения взаимодействующих тел (частей тела).
- Потенциальная энергия изменяется только при совершении работы.
Расчет потенциальной энергии
Кинетическая энергия тела, зависящая от его массы и скорости, выражается формулой 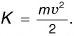
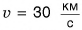
Рассмотрим отдельно два случая: потенциальную энергию притяжения поднятого над поверхностью Земли тела и потенциальную энергию деформированного тела.
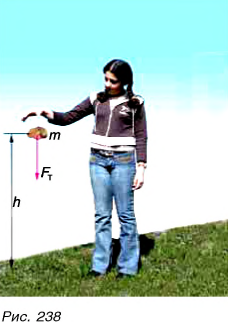
В первом случае формулу для расчета потенциальной энергии легко вывести. Если тело массой m поднято относительно поверхности Земли на высоту h (рис. 238), то при его падении сила тяжести 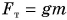
Это и есть потенциальная энергия поднятого тела:
Значение потенциальной энергии относительно. Так, относительно пола потенциальная энергия светильника (рис. 239) массой m = 1,0 кг, центр тяжести которого расположен на высоте 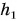
Относительно потолка 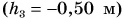
Поэтому, приводя значение потенциальной энергии, необходимо указывать уровень, относительно которого она задана, — нулевой уровень потенциальной энергии (это может быть, к примеру, поверхность пола, потолка, стола и т. д.).
Гораздо сложнее дело обстоит с расчетом потенциальной энергии деформированного тела. Мы можем растянуть или сжать пружину, изогнуть или закрутить ее (рис. 240). Потенциальная энергия у пружины будет в каждом из этих случаев. И чем больше упругая деформация, тем больше потенциальная энергия пружины. В данном примере расчет потенциальной энергии придется вести по различным формулам. Более детально с этим вы будете знакомиться в 9-м классе.
Главные выводы:
- Потенциальная энергия притяжения тела к Земле зависит от массы тела и высоты его подъема над нулевым уровнем энергии.
- Значение потенциальной энергии тела зависит от выбора нулевого уровня энергии.
- Потенциальная энергия деформированного тела зависит от величины деформации.
Пример решения задачи:
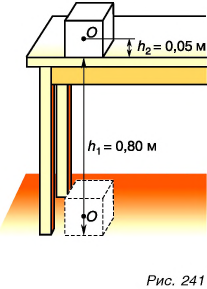
Парафиновый однородный кубик с длиной ребра а = 10 см лежит на столе на высоте 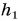
Дано:
Решение:
Потенциальная энергия кубика относительно поверхности пола (рис. 241) определяется положением его центра (точки O):
Масса кубика 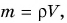
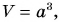
Потенциальная энергия кубика относительно поверхности стола:
Работа по подъему кубика на высоту 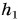
Ответ:
Закон сохранения механической энергии
Кинетическая и потенциальная энергии — это два вида механической энергии. Связаны ли они друг с другом? И если да, то в чем выражается эта связь?
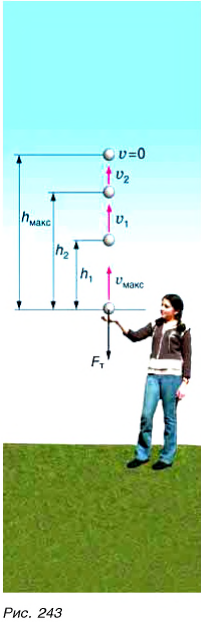
Проследим за движением брошенного вверх металлического шарика (рис. 243). В нижней точке траектории сила действия руки на шарик сообщает ему кинетическую энергию. Шарик движется вверх. Скорость его движения, а значит, и кинетическая энергия уменьшаются. Но исчезает ли кинетическая энергия бесследно? Поднимаясь выше, шарик приобретает все большую потенциальную энергию (вспомните: 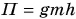
Если сопротивление воздуха мало (и им можно пренебречь), брошенный вверх шарик возвращается назад практически с такой же, как в момент бросания, скоростью и кинетической энергией.
А каким будет значение механической энергии шарика в промежуточных точках? Например, на высоте 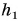
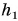
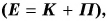
Если силами трения или сопротивления движению нельзя пренебречь, этот закон не выполняется. Заменим в опыте металлический шарик на пенопластовый брусок такой же массы (рис. 244). Мы увидим, что даже при большей, чем у металлического шарика, начальной скорости он не поднимется на такую же высоту и вернется назад с заметно меньшей скоростью. Убывает кинетическая энергия движущейся по горизонтальной поверхности льда шайбы, но потенциальная энергия взамен не появляется. За счет кинетической энергии шайбы совершается работа против сил трения.
В заключение заметим, что явление превращения энергии из одного вида в другой человек научился использовать в практических целях. Энергия падающей воды приводит в действие водяные мельницы и гидроэлектростанции. В Республике Беларусь успешно реализуется государственная программа использования энергии рек. Важная роль в ней отводится таким рекам, как Неман и Западная Двина. Па Немане работает Гродненская ГЭС мощностью 17 МВт. Установленная мощность Витебской ГЭС на Западной Двине — 40 МВт.
Кинетическую энергию ветра человек с давних времен начал использовать с помощью паруса (рис. 245), затем стал применять в ветряных мельницах. В последние годы в нашей стране начато сооружение ветроэлектростанций (рис. 246). Они уникальны тем, что не оказывают вредного воздействия на окружающую среду. Во многих странах успешно используют энергию приливов и отливов вод морей и океанов. Там созданы приливные электростанции.
Главные выводы:
- Кинетическая и потенциальная энергии взаимо-превращаемы.
- При отсутствии сил трения и сопротивления движению полная механическая энергия тела (системы тел) сохраняется.
- Закон сохранения механической энергии не выполняется, если силами трения (сопротивления) нельзя пренебречь.
- Заказать решение задач по физике
Пример решения задачи:
Камень бросили вертикально вверх со скоростью 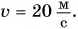
Дано:
Решение:
За нулевой уровень потенциальной энергии примем уровень O — O, проходящий через точку бросания камня (рис. 247). Значит,
Полная механическая энергия камня в точке бросания 1:
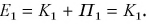
Полная механическая энергия камня в точке 2:
По условию 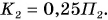
Ответ:
Энергия и работа
Энергия – эта количественная мера различных форм движения и взаимодействия (по гречески слово «энергия» означает действие). Энергия в зависимости от вида движения в природе проявляется по-разному. Например, механическая, тепловая, электромагнитная, ядерная энергия и другие. В результате взаимодействия энергия одного вида превращается в энергию другого вида. Однако во всех этих процессах энергия, переданная от одного тела второму (независимо от ее вида), будет равна энергии, полученной вторым телом от первого.
Как известно из второго закона Ньютона, чтобы изменить механическое движение тела на него должны подействовать другие тела. Иначе говоря, среди этих тел происходит обмен энергиями. Для описания такого обмена энергии в механике введено понятие механическая работа, которую принято обозначать буквой 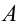
Механическая работа. Величина, равная скалярному произведению силы на перемещение в направлении действия силы, называется механической работой, т.е.
Здесь: 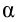
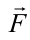
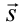
Если учитывать, что 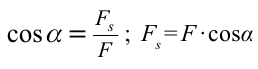
Здесь 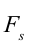
Основываясь на выражении (3.2), можно сделать следующий вывод:
если 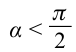
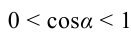
если 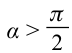
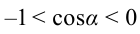
если 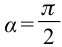
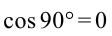
Работа считается аддитивной (аддитив – по-латински означает суммарный) величиной (в физике аддитивность величины означает, что величина, относящаяся к системе в целом, равна сумме величины, относящихся к ее составным частям).
Если на тело действует несколько сил, то будет:
тогда полная работа равна работе, выполненной равнодействующей сил.
или
Единица работы. Единица измерения работы в системе СИ – Джоуль (Дж):
В качестве единицы работы в СИ принята работа выполненная силой 1Н при смещении тела на 1 м.
Работа силы тяжести. На поверхности Земли на тело действует сила тяжести со стороны Земли, равная 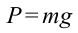
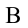
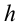
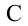
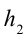
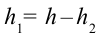
Здесь выполненная силой тяжести работа выражается следующей формулой:
Здесь: 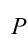
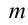
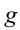
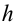
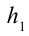
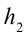
Работа, выполненная силой тяжести, не зависит от формы пути, зависит только от высоты спуска. Поэтому работа, выполненная под действием силы тяжести, зависит не от формы траектории, а от начального и конечного состояний. Такая сила называются потенциальной или консервативной. Поле такой силы называется потенциальным полем.
При движении тела вниз из-за соответствия направления силы тяжести и смещения выполненная работа будет положительной, при движении вверх из-за противоположности направлений работа будет отрицательной. Поэтому в случае, когда тело под воздействием силы тяжести смещено и вернулось обратно, выполненная общая работа равняется нулю.
Полной механической энергией системы называется сумма кинетической и потенциальной энергии системы. Например, полная механическая энергия тела массой 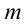
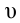
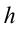
Полная механическая энергия системы остается неизменной с течением времени:
Возможны лишь превращения потенциальной энергии и кинетическую и обратно. Выражение (3.5) представляет собой закон сохранения механической энергии.
Проведенные многочисленные эксперименты, теоретические выводы подтвердили строгое соблюдение закона сохранения энергии.
В природе постоянно происходят превращения одного вида энергии в другой (например, механическая энергия переходит в тепловую энергию). Поэтому этот закон также называют законом сохранения и превращения энергии. Этот закон является основным законом природы и действителен не только для макроскопических, но и микроскопических систем.
Энергия никогда не исчезает, ниоткуда не появляется, она может только преобразовываться из одного вида в другой.
В закрытых системах полная энергия сохраняется.
Например, потенциальная энергия тела, падающего с высоты 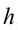
Коэффициент полезного действия. Введена величина, показывающая, какая часть израсходованной энергии машин и двигателей превращается в полезную работу.
Отношение полезной работы к полной работе называется коэффициентом полезного действия (КПД) и обозначается буквой 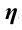
Если полезную работу обозначить 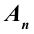
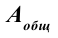
КПД не может быть больше единицы (100%). В машинах и двигателях в результате работы силы трения часть полной энергии расходуется и поэтому КПД всегда меньше единицы.
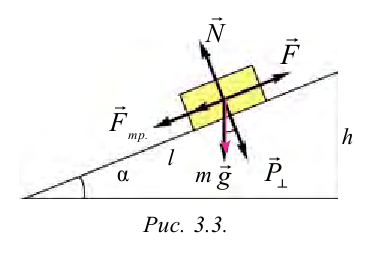
Рассмотрим наклонную плоскость и выполненную работу при подъеме тела вверх. По «золотому правилу» механики, во сколько раз выигрываем в силе, во столько раз проиграем в расстоянии. Но из-за увеличения расстояния смещения не меняется выполненная работа.
Рассмотрим груз с весом 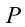
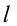
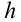
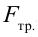
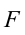
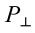
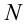
Если не учитывать силу трения, получим уравнение:
Однако с учетом силы трения,
Тогда 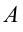
Коэффициент полезного действия:
Сила притяжения, действующая на груз, равна:
- Движение и силы
- Давление в физике
- Строение вещества в физике
- Физическое тело и вещество в физике
- Золотое правило механики
- Потенциальная энергия
- Кинетическая энергия
- Закон сохранения и превращения механической энергии
Мощность как физическая величина, формула мощности
Значение, показывающее, как быстро происходят преобразование, трансляция или потребление энергии в какой-либо системе, – мощность. Для характеристик энергетических условий важно, насколько быстро выполняется процесс. Работа, реализуемая в единицу времени, именуется мощностью:
P = А/t,
где:
- А – работа;
- t – время.
Можно учитывать отдельно мощность в механике и электрическую мощность.
Чтобы получить ответ на вопрос: в чем измеряется механическая мощность, рассматривают действие силы на движущееся тело. Сила проделывает работу, мощность в таком случае определяется по формуле:
N = F*v,
где:
- F – сила;
- v – скорость.
При вращательном движении эту величину определяют с учётом момента силы и частоты вращения, «об./мин.».
Мощность
| Мощность | |
| N , P , W = d A d t >> | |
| СИ | Вт |
| СГС | эрг·с −1 |
Мо́щность
— скалярная физическая величина, равная в общем случае скорости изменения, преобразования, передачи или потребления энергии системы. В более узком смысле мощность равна отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени [1] .
Зависимость между электрическим током и мощностью
Плотность тока — что это такое и в чем измеряется
В электротехнике работой будет U – напряжение, которое перемещает 1 кулон, количество перемещаемых в единицу времени кулонов – это ток (I). Мощность электротока или электрическую мощность P получают, умножив ток на напряжение:
P = U*I.
Это полная работа, выполненная за 1 секунду. Зависимость здесь прямая. Изменяя ток или напряжение, изменяют мощность, расходуемую устройством.
Одинакового значения Р добиваются, варьируя одну из двух величин.
Как измеряют мощность разных видов
Измерение разных мощностных видов происходит по формулам, выведенным с конца прошлого и позапрошлого столетия. Для каждой разновидности есть свое точное алгебраическое правило. Так, измерить механическую можно по первой формуле, а электрическую по второй. Что касается гидравлической, ее можно вычислить по третьему алгебраическому правилу.
Механическая
Механической мощностью является скалярный вид произведения силового вектора на скоростной вектор, при котором движется какой-то объект. Исходя из формулы для вычисления этого показателя, чтобы отыскать его, необходимо знать показатель вектора силы со скоростным вектором, а последний из них равен модулю силы, перемноженному на модуль скорости и векторный угол скорости с силой.
Что касается вычисления тела, которое совершает вращательные движения, можно отметить, что нужно иметь представление о показателе момента силы с угловой скоростью.
Вам это будет интересно Как устроен вольтметр, принцип действия и назначение прибора
Дополнительная информация! Если в задаче эти данные неизвестны, можно двукратное число Пи перемножить на частоту вращения в минуту на момент силы, а затем полученные сведения поделить на 60. Таким образом совершаются вычисления в механике, если нужно понять, какую силу имеет двигатель или прочий силовой агрегат.
Электрическая
Электрической мощностью называется величина, которая показывает, с какой скоростью или преобразованием двигается электрическая энергия. Для изучения мгновенной электрической мощностной характеристики на определенном участке цепи, необходимо знать значение тока и напряжения мгновенного тока и перемножить данные значения.
Чтобы понять, сколько составляет активный, полный, реактивный или мгновенный реактивный мощностный показатель, нужно знать точные цифры амплитуды тока, амплитуды напряжения, угла тока с напряжением, а также угловую скорость и время, поскольку все существующие физические формулы сводятся к этим параметрам. Также в формулах задействуется синус, косинус угла и значение 1/2.
Гидравлическая
Гидравлическим мощностным показателем в гидромашине или гидроцилиндре называется произведение машинного перепада давления на жидкостный расход. Как правило, это основная формулировка, взятая из единственной существующей формулы для вычисления.
Обратите внимание! Больше алгебраических и инженерных правил можно найти в прикладной науке о движениях жидкостей и газов, а именно в гидравлике.
Постоянного и переменного тока
Что касается мощности постоянного с переменным током, то чаще всего их причисляют к электрической разновидности. Конкретного понятия для двух разновидностей нет, однако их можно вычислить, исходя из имеющихся алгебраических установок. Так, мощностью постоянного тока является произведение силы тока и постоянного напряжения или же удвоенное значение силы тока на электрическое сопротивление, которое, в свою очередь, вычисляется делением двойного напряжения на обычное сопротивление.
Что касается переменного тока, это произведение силы тока с напряжением и косинусом сдвига фаз. При этом беспрепятственно можно посчитать только активную и реактивную разновидность. Узнать полное мощностное значение можно через векторную зависимость этих показателей и площади.
Чтобы измерить эти показатели, можно воспользоваться как указанными выше приборами, так и фазометром. Этот прибор служит, чтобы вычислить реактивную разновидность по государственному эталону.
Вам это будет интересно Принцип действия и устройство магнитоуправляемого геркона
В целом, мощность — это величина, основное предназначение которой показывать силу работы конкретного прибора и во многих случаях скорость деятельности, взаимодействуя с ним. Она бывает механической, электрической, гидравлической и для постоянного с переменным током. Измеряется по международной системе в ваттах и киловаттах. Приборами для ее вычисления выступает вольтметр, ваттметр. Основные формулы для самостоятельного расчета перечислены выше.
Определение единицы измерения мощности тока
Единица измерения мощности тока носит имя Джеймса Ватта, шотландского инженера-механика. 1 Вт – это мощность, которую вырабатывает ток 1 А при разности потенциалов 1 В.
кВа в кВт — как правильно перевести мощность
К примеру, источник при напряжении 3,5 В создаёт в цепи ток 0,2 А, тогда мощность тока получится:
P = U*I = 3,5*0,2 = 0,7 Вт.
Внимание! В механике мощность принято изображать буквой N, в электротехнике – буквой P. В чем измеряется n и P? Независимо от обозначения, это одна величина, и измеряется она в ваттах «Вт».
Мощность: определение, формула расчета, единица измерения.
Мощность — физическая величина, измеряемая отношением работы к промежутку времени, в течение которого она произведена.
Другими словами, мощность показывает, какая работа совершается за единицу времени (в СИ — за 1 с). Мощность определяется формулой:
.
где N — мощность, А — работа, совершенная за время М. Подставив в формулу вместо работы А ее выражение , получим:
Мощность равна произведению модулей векторов силы и скорости на косинус угла между этими векторами.
Мощность в системе СИ измеряется в ваттах (Вт). Один ватт (1 Вт) — это такая мощность, при которой за 1 с совершается работа 1 Дж: 1 Вт = 1 Дж/с.
Эта единица названа в часть английского изобретателя Дж. Ватта (Уатта), построившего первую паровую машину. Сам Дж. Ватт (1736-1819) пользовался другой единицей мощности — лошадиной силой (л. с), которую он ввел для того, чтобы можно было сравнивать работоспособности паровой машины и лошади: 1 л. с. = 735,5 Вт.
В технике часто применяются более крупные единицы мощности — киловатт и мегаватт: 1 кВт = 1000 Вт, 1 МВт = 1000000 Вт.
Основные положения молекулярно-кинетической энергии и их опытные обоснования.
· Все тела состоят из частиц – атомов, молекул, ионов.
· Все частицы находятся в непрерывном хаотическом тепловом движении.
· Между частицами любого тела существуют силы взаимодействия – притяжения и отталкивания.
Таким образом, в молекулярно-кинетической теории объектом исследования является система, состоящая из большого количества частиц – макросистема. Для объяснения поведения такой системы законы механики не применимы. Поэтому основным методом исследования является статистический методизучения свойств вещества.
Для объяснения и предсказания явлений важно знатьосновные характеристики молекул:
Размеры
Оценка размера молекулы может быть сделана как размер кубика a в котором содержится одна молекула, исходя из плотности твердых или жидких веществ и массы одной молекулы:
Масса молекулОтношение массы вещества m к числу молекул N в данном веществе:
Относительная молекулярная массаОтношение массы молекулы (или атома) данного вещества к 1/12 массы атома углерода:
Количество вещества
Количество вещества равно отношению числа частиц N в теле (атомов – в атомарном веществе, молекул – в молекулярном) к числу молекул в одном моле веществаNА:
Постоянная Авогадро
Количество молекул, содержащихся в 1 моль вещества.
Молярная масса
Молярной массой вещества называют массу вещества, взятого в количестве 1 моля.
В Международной системе единиц молярная масса вещества выражается в кг/моль.
Взаимодействие (количественно на основе опытов)
Молекулярно-кинетическая теория дает возможность понять, почему вещество может находиться в газообразном, жидком и твердом состояниях. С точки зрения МКТ агрегатные состояния различаются по значению среднего расстояния между молекулами и характеру движения молекул друг относительно друга.
Основные положения молекулярно-кинетической теории неоднократно подтверждались различными физическими экспериментами. Например, исследованием:
Диффу́зия — процесс взаимного проникновения молекул или атомов одного вещества между молекулами или атомами другого, приводящий к самопроизвольному выравниванию их концентраций по всему занимаемому объёму. В некоторых ситуациях одно из веществ уже имеет выравненную концентрацию и говорят о диффузии одного вещества в другом. При этом перенос вещества происходит из области с высокой концентрацией в область с низкой концентрацией (вдоль вектора градиента концентрации).
Ватт и другие единицы измерения мощности
Говоря о том, в чем измеряется мощность, необходимо знать, о чём идёт речь. Ватт – это величина, соответствующая 1 Дж/с. Она принята в Международной Системе Единиц. В каких единицах ещё измеряется мощность? Раздел науки астрофизика работает с единицей под названием эрг/с. Эрг – очень маленькая величина, равная 10-7 Вт.
Формула механической мощности — средняя и мгновенная мощность
Ещё одна, поныне распространённая, единица из этого ряда – «лошадиная сила». В 1789 году Джеймс Ватт подсчитал, что груз весом 75 кг из шахты может вытащить одна лошадь и сделать это со скоростью 1 м/с. Исходя из подсчёта такой трудоёмкости, мощность двигателей допускается измерить этой величиной в соотношении:
1 л.с. = 0,74 кВт.
Интересно. Американцы и англичане считают, что 1 л.с. = 745.7 Вт, а русские – 735.5 Вт. Спорить, кто прав, а кто нет, не имеет смысла, так как мера эта внесистемная и не должна быть использована. Международная организация законодательной метрологии рекомендует изъять её из обращения.
В России при расчёте полиса КАСКО или ОСАГО используют эти данные силового агрегата автомобиля.
Единицы измерения
В Международной системе единиц (СИ) единицей измерения мощности является ватт (Вт), равный одному джоулю в секунду (Дж/с). В теоретической физике, астрофизике, в качестве единицы для мощности часто используют эрг в секунду (эрг/с).
Другой распространённой, но ныне устаревшей единицей измерения мощности, является лошадиная сила. В своих рекомендациях Международная организация законодательной метрологии (МОЗМ) относит лошадиную силу к числу единиц измерения, «которые должны быть изъяты из обращения как можно скорее там, где они используются в настоящее время, и которые не должны вводиться, если они не используются» [2] .
Соотношения между единицами мощности
| Единицы | Вт | кВт | МВт | кгс·м/с | эрг/с | л. с.(мет.) | л. с.(анг.) |
| 1 ватт | 1 | 10 −3 | 10 −6 | 0,102 | 10 7 | 1,36·10 −3 | 1,34·10 −3 |
| 1 киловатт | 10 3 | 1 | 10 −3 | 102 | 10 10 | 1,36 | 1,34 |
| 1 мегаватт | 10 6 | 10 3 | 1 | 102·10 3 | 10 13 | 1,36·10 3 | 1,34·10 3 |
| 1 килограмм-сила-метр в секунду | 9,81 | 9,81·10 −3 | 9,81·10 −6 | 1 | 9,81·10 7 | 1,33·10 −2 | 1,31·10 −2 |
| 1 эрг в секунду | 10 −7 | 10 −10 | 10 −13 | 1,02·10 −8 | 1 | 1,36·10 −10 | 1,34·10 −10 |
| 1 лошадиная сила (метрическая) | 735,5 | 735,5·10 −3 | 735,5·10 −6 | 75 | 7,355·10 9 | 1 | 0,9863 |
| 1 лошадиная сила (английская) | 745,7 | 745,7·10 −3 | 745,7·10 −6 | 76,04 | 7,457·10 9 | 1,014 | 1 |
Формула взаимосвязи между мощностью, напряжением и силой тока
В электротехнике работу рассматривают как некоторое количество энергии, отдаваемое источником питания на действие электроприбора в период времени. Поэтому электрическая мощность есть величина, описывающая быстроту трансформации или передачи электроэнергии. Её формула для постоянного тока выглядит так:
P = U*I,
где:
- U – напряжение, В;
- I – сила тока, А.
Для некоторых случаев, пользуясь формулой закона Ома, мощность можно вычислить, подставив значение сопротивления:
P = I*2*R, где:
- I – сила тока, А;
- R – сопротивление, Ом.
В случае расчётов мощности цепей переменного тока придётся столкнуться с тремя видами:
- активная её формула: P = U*I*cos ϕ, где – коэффициент угла сдвига фаз;
- реактивная рассчитывается: Q = U*I*sin ϕ ;
- полная представлена в виде: S = √P2 + Q2, гдe P – aктивная, а Q2 – реактивная.
Расчёты для однофазной и трёхфазной цепей переменного тока выполняются по разным формулам.
Важно! Потребители электроэнергии на предприятиях в большинстве асинхронные двигатели, трансформаторы и другие индуктивные приёмники. При работе они используют реактивную мощность, а та, протекая по линиям электропередач, приводит ЛЭП к дополнительной нагрузке. Чтобы повысить качество энергии, используют компенсацию реактивной энергии в виде конденсаторных установок.
Формулы для измерения
Мощность — величина, которая непосредственным образом связана с другими показателями. Так, она прямым образом связана со временем, силой, скоростью, вектором силы и скоростью, модулем силы и скорости, моментом силы и частотой вращения. Нередко в формулах при вычислении электрической мощностной разновидности задействуется также число Пи, показатель сопротивления, мгновенный ток с напряжением на конкретном участке электрической сети, активная, полная и реактивная сила. Непосредственным участником в вычислении является амплитуда с угловой скоростью и начальной силой тока с напряжением.
Вам это будет интересно Расцветка шин по фазам
В расчетах гидравлической мощностной разновидности, принимает участие давление и расход жидкости. Нередко берется в расчеты показатель количества оборотов двигателя за конкретный промежуток времени.
Дополнительная информация! Чтобы рассчитать тягу, коэффициент полезного действия с другими рабочими параметрами устройства, изучается температура, сила трения и проводниковое сопротивление с реактивными нагрузками.
Приборы для измерения электрической мощности
Провести измерения мощности позволяет ваттметр. У него две обмотки. Одна включается в цепь последовательно, как амперметр, вторая параллельно, как вольтметр. В установках электроэнергетики ваттметры определяют значения в киловатт-час «кВт*час». В измерениях нуждается не только электрическая, а также лазерная энергия. Приборы, способные измерять этот показатель, изготавливаются как стационарного, так и переносного исполнения. С их помощью оценивают уровень лазерных излучений оборудования, применяющего этот вид энергии. Один из портативных измерителей – LP1, японского производителя. LP1 разрешает напрямую определять значения силы светового излучения, к примеру, в визуальном пятне оптических устройств проигрывателей DVD.
Электрическая мощность
Основная статья: Электрическая мощность
Электри́ческая мощность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.
Мгновенная электрическая мощность P ( t ) {displaystyle P(t)} участка электрической цепи:
P ( t ) = I ( t ) ⋅ U ( t ) {displaystyle P(t)=I(t)cdot U(t),} где I ( t ) {displaystyle I(t)} — мгновенный ток через участок цепи; U ( t ) {displaystyle U(t)} — мгновенное напряжение на этом участке.
При изучении сетей переменного тока, помимо мгновенной мощности, соответствующей общефизическому определению, вводятся также понятия:
- активной мощности, равной среднему за период значению мгновенной мощности, мгновенная активная мощность:
p ( t ) = 1 2 ⋅ U m ⋅ I m ⋅ cos φ − 1 2 ⋅ U m ⋅ I m ⋅ cos φ cos ( 2 ω t ) . {displaystyle p(t)={1 over 2}cdot U_{m}cdot I_{m}cdot cos varphi -{1 over 2}cdot U_{m}cdot I_{m}cdot cos varphi cos(2omega t).}
- реактивной мощности, которая соответствует энергии, циркулирующей без диссипации от источника к потребителю и обратно, мгновенная реактивная мощность:
при φ > 0 : {displaystyle varphi >0{:}} q ( t ) = 1 2 ⋅ U m ⋅ I m ⋅ sin φ ⋅ cos ( 2 ω t + π 2 ) , {displaystyle q(t)={frac {1}{2}}cdot U_{m}cdot I_{m}cdot sin varphi cdot cos {Bigl (}2omega t+{frac {pi }{2}}{Bigr )},} при φ < 0 : {displaystyle varphi <0{:}} q ( t ) = 1 2 ⋅ U m ⋅ I m ⋅ sin φ ⋅ cos ( 2 ω t − π 2 ) . {displaystyle q(t)={frac {1}{2}}cdot U_{m}cdot I_{m}cdot sin varphi cdot cos {Bigl (}2omega t-{frac {pi }{2}}{Bigr )}.}
- полной мощности, вычисляемой как произведение действующих значений тока и напряжения без учёта сдвига фаз. мгновенная полная мощность:
s ( t ) = 1 2 ⋅ U m ⋅ I m ⋅ cos φ − 1 2 ⋅ U m ⋅ I m ⋅ c o s ( 2 ω t − φ ) , {displaystyle s(t)={1 over 2}cdot U_{m}cdot I_{m}cdot cos varphi -{1 over 2}cdot U_{m}cdot I_{m}cdot cos{Bigl (}2omega t-varphi {Bigr )},} где I m {displaystyle I_{m}} — амплитуда тока; U m {displaystyle U_{m}} — амплитуда напряжения; φ {displaystyle varphi } — угол между начальным углом напряжения ψ u {displaystyle psi _{u}} и начальным углом силы тока ψ i {displaystyle psi _{i}} — ( φ = ψ u − ψ i ) ; {displaystyle (varphi =psi _{u}-psi _{i}){;}} ω {displaystyle omega } — угловая скорость; t {displaystyle t} — время.
Приборы для измерения электрической мощности и мощности излучения
Вы поможете проекту, исправив и дополнив его.
Аналоговый стрелочный ваттметр
- Ваттметры (в том числе варметры) — измерительные приборы, предназначенные для определения мощности электрического тока или электромагнитного излучения.
По назначению и диапазону частот ваттметры можно разделить на три категории — низкочастотные (и постоянного тока), радиочастотные и оптические.
Ваттметры радиодиапазона по назначению делятся на два вида: проходящей мощности, включаемые в разрыв линии передачи, и поглощаемой мощности, подключаемые к концу линии в качестве согласованной нагрузки. В зависимости от способа функционального преобразования измерительной информации и её вывода оператору ваттметры бывают аналоговые (показывающие и самопишущие) и цифровые.
Мощность в бытовых электрических приборах
Для нагрева металла нити накаливания лампочки, увеличения температуры рабочей поверхности утюга или иного бытового прибора, тратится определённое количество электроэнергии. Её величину, отбираемую нагрузкой за час, считают потребляемой мощностью этого аппарата.
Внимание! Если на лампочке написано «40 W, 230 V», это значит, что за 1 час она потребляет из сети переменного тока 40 Вт. Зная количество лампочек и параметры, подсчитывают, сколько энергии тратится на освещение комнат в месяц.
Мощность некоторых электрических приборов, Вт
Средние значения потребления электроэнергии бытовых устройств:
- плиты – 110006000 Вт;
- холодильники – 150-600 Вт;
- стиральные машины – 1000-3000 Вт;
- пылесосы – 1300-4000 Вт;
- электрочайники – 2000-3000 Вт.
Параметры каждого бытового прибора указываются в паспорте, а также обозначаются на корпусе. Там определены точные значения для информации потребителя.
Механическая работа, мощность и КПД механизма
1. Механическая работа (или работа силы над телом) – физическая величина, равная по модулю произведению силы на путь, пройденный телом вдоль направления этой силы. Если вектор силы перпендикулярен направлению движения тела, то совершаемая этой силой работа равна нулю; если вектор силы сонаправлен с направлением движения тела, то работу силы считают положительной; если вектор силы противоположен направлению движения тела, то работу силы считают отрицательной.
- В случае, когда точка приложения силы перемещается в направлении действия силы, механическая работа А равна произведению модуля F силы на путь s, пройденный точкой приложения силы: А = Fs.
- Единица работы в СИ 1 Джоуль (Дж) = 1 Нм.
- «Золотое правило» механики с использованием понятия работы: никакой простой механизм не дает выигрыша в работе.
Таблица «Механическая работа, мощность и КПД»
2. Коэффициент полезного действия (КПД) – физическая величина, равная отношению полезной работы к полной совершённой работе. КПД показывает долю полезной работы от полной и, как и все доли, всегда имеет положительный знак и не имеет «своей» единицы для измерения. Значение КПД обычно выражают в процентах, которое нужно переводить в десятичную дробь для дальнейших вычислений.
- Коэффициентом полезного действия (КПД) механизма называют отношение полезной работы Апол к совершенной Асов, выраженное в процентах: η = Апол/Асов · 100%.
- КПД любого реального механизма меньше 100 % (из-за трения и из-за того, что сами механизмы и их части имеют некоторую массу).
3. Мощность действия – физическая величина, равная отношению механической работы ко времени, за которое она была совершена. Мощность характеризует быстроту (скорость) совершения работы. Мощность принято вычислять только для тех действий, в которых механическая работа положительна.
- Мощностью N называют отношение совершенной работы А к промежутку времени t, за который эта работа совершена: N = A/t
- Единица мощности в СИ 1 ватт (Вт) = 1 Дж/с.
- Мощность можно выразить через силу и скорость с помощью формулы N = Fv.
Схема «Механическая работа. Мощность»
Конспект урока по физике в 7 класса «Механическая работа и энергия».
Смотреть задачи: 1) на механическую работу, 2) механическую мощность, 3) на КПД простых механизмов.
Следующая тема: «Простые механизмы. Блоки»
Работа силы. Мощность
Физика10 класс
Материалы к уроку
-
18. Работа силы. Мощность.doc
51 KBСкачать
-
18. Работа силы. Мощность.ppt
8.44 MBСкачать
Конспект урока
Ежедневно, совершенно не задумываясь, мы, используя наши мышцы, либо приводим в движение окружающие нас предметы и поддерживаем это движение, либо же останавливаем движущиеся тела.
Этими телами являются орудия труда, например, топор, карандаш, пила.
В различных играх мы перемещаем мячи, клюшки, шайбы, шахматные фигуры.
На производстве и в сельском хозяйстве люди также приводят в движение различные орудия труда.
Правда, в последнее время роль простых рабочих постепенно сводится к управлению механизмами. Но в каждом механизме можно увидеть аналоги простых орудий ручного труда. Например, в швейной машинке имеется игла, ковш экскаватора заменяет лопату.
Применение современных машин во много раз увеличивает производительность труда благодаря использованию в них двигателей. Назначение любого двигателя состоит в том, чтобы приводить в движение тела или их части, а также поддерживать это движение, преодолевая
торможение как обычным трением, так и «рабочим» сопротивлением. Так резец не должен просто скользить по материалу, а, врезаясь в него, разрезать материал, или снимать стружку. Плуг комбайна используется для того, чтобы взрыхлять землю. При этом на резец или на плуг должна действовать со стороны двигателя сила, точка приложения которой перемещается вместе с резцом или плугом.
Когда человек или двигатель воздействует с определенной силой на тело, которое находится в движении, то мы считаем, что он совершает работу. Это обыденное понятие о работе легло в основу формирования одного из самых важных понятий механики — понятия работы силы.
В окружающем нас мире работа совершается постоянно, когда на какое-либо тело в направлении его движения или же в противоположную сторону действует сила. Это может быть одна сила или несколько сил. Она может действовать со стороны одного другого тела или нескольких других тел. Так, сила притяжения совершает работу при падении камня с обрыва. В это же время совершают работу и силы трения, которые действуют на камень со стороны воздуха.
Также совершает работу и сила упругости, когда распрямляется согнутое из-за ветра дерево.
Применяя второй закон Ньютона в импульсной форме, мы можем рассчитать изменение скорости тела по модулю и направлению, зная приложенную к телу силу и время ее действия.
Во многих случаях важно уметь рассчитывать изменение скорости по модулю, если при перемещении тела на него действует сила. В механике используется особая физическая величина, характеризующая воздействия на тела сил, приводящих к изменению модуля их скорости. Эту величину называют работой силы, она зависит от действующей силы и от перемещения тела в результате действия этой силы.
Сила, направленная перпендикулярно скорости, а значит, и перемещению, изменяет скорость только по направлению, но не по модулю. Такое движение происходит при равномерном движении по окружности, когда ускорение тела, а значит, и приложенная к нему сила, перпендикулярны скорости.
Модуль вектора скорости изменяется только в том случае, когда проекция силы на направление перемещения тела не равна нулю. Именно эта проекция определяет, какое действие оказывает сила, изменяющая скорость тела по модулю. Совершает работу проекция вектора силы. Следовательно, работу можно рассматривать как произведение проекции вектора силы на направление перемещения тела на модуль вектора перемещения.
Если угол между силой и перемещением обозначить как альфа, тогда проекция вектора силы на направление перемещения равна произведению модуля вектора силы на косинус угла альфа.
Получаем, что работа силы равна произведению модулей силы и перемещения точки приложения силы и косинуса угла между ними.
Эта формула справедлива только в том случае, когда сила постоянна и тело движется вдоль прямой линии. Если траектория движения тела криволинейна, а сила, действующая на него изменяется, траекторию движения тела разделяют на бесконечно малые отрезки, которые можно считать прямолинейными, а силу на них постоянной.
Работа, в отличие от силы и перемещения, является не векторной, а скалярной величиной. Она может быть положительной, отрицательной или равной нулю. Работа силы является отрицательной, если эта сила мешает движению тела; положительной – если сила помогает движению; и работа силы равна нулю, если сила не препятствует и не помогает движению тела.
Знак работы определяется знаком косинуса угла между силой и перемещением. Если угол меньше 90 градусов, работа силы величина положительная, так как косинус острых углов больше нуля.
При угле больше 90 градусов работа отрицательна, так как косинус тупых углов меньше нуля. В этом случае сила препятствует движению.
При угле равном 90 градусов сила перпендикулярна перемещению, косинус такого угла равен нулю, работа этой силой не совершается. Примером может служить сила тяжести, которая не совершает работу при перемещении тела по горизонтальной поверхности. При движении спутника по круговой орбите сила всемирного тяготения также не совершает работу.
В случае, когда на тело действует несколько сил, проекцию результирующей силы на перемещение можно вычислить как сумму проекций отдельных сил. Поэтому работа результирующей силы равна сумме произведений проекций каждой из действующих сил на направление перемещения на модуль вектора перемещения. Или полная работа нескольких сил равна сумме работ всех сил, действующих на тело.
Единица работы может быть установлена с помощью основной формулы: работа силы равна произведению модулей силы и перемещения точки приложения силы и косинуса угла между ними. Если при одинаковом направлении силы и перемещения к телу приложена сила, модуль которой равен единице, и тело перемещается на единицу длины, то и работа силы будет равна единице. В Международной системе единиц работа измеряется в джоулях.
Джоуль — это работа, совершаемая силой один ньютон при перемещении один метр, если направления силы и перемещения совпадают.
Одна и та же работа может быть выполнена очень быстро – за маленький промежуток времени или медленно – в течение большого интервала времени. На практике, однако, имеет большое значение быстро или медленно была выполнена работа. Производительность любого двигателя характеризуется временем, в течение которого выполняется работа. Достаточно большую работу может совершить и вполне небольшой электромоторчик, но для этого понадобится очень много времени. Однако более мощному мотору для этого понадобится гораздо меньше времени. Примером могут служить два электронасоса: небольшой производительности и более производительный. Оба они могут заполнить водой одинаковые по емкости бассейны, но меньшему насосу для этого потребуется значительно бОльшее время.
Физическая величина, характеризующая скорость, с которой выполняется работа, это мощность.
Мощностью называют отношение работы к интервалу времени, за который эта работа совершена.
Мощность численно равна работе, совершенной в единицу времени.
Заменяя в формуле мощности работу ее выражением, получим, что мощность равна произведению модуля вектора силы на модуль вектора скорости тела и на косинус угла между их направлениями.
Понятие мощности вводится для оценки работы за единицу времени, совершаемой каким-либо механизмом — насосом, подъемным краном, мотором машины. Поэтому в полученных формулах под силой подразумевается сила тяги.
В Международной системе единиц мощность выражается в ваттах. Мощность равна 1 ватт, если работа 1 джоуль совершается за 1 секунду.
Наряду с ваттом используются более крупные единицы мощности:
1 гектоватт равен 100 ваттам,
1 киловатт равен 1000 ваттам,
1 мегаватт равен 1000000 ваттам.
Мощность можно повысить как за счет увеличения действующих сил, так и за счет увеличения скорости движения.
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ