Мекки Мессер является владельцем маленькой компании, которая выпускает электрические ножи. В среднем Мекки может производить 150 ножей в день. Дневной спрос на ножи примерно равен 40. Фиксированные издержки производства равны 100 тыс. руб., издержки хранения – 8 тыс. руб. за нож в год. Какой максимальный заказ следует иметь на складе?
—————————-
Дано:
alpha = 150 ед. в день
beta = 40 ед.
h(издержки хранения) = 8 тыс.руб. в год
К(издержки производства) = 100 тыс.руб
Помогите пожалуйста решить задачу, думаю сначала нужно найти оптимальное значение размера заказа по формуле
, у меня получилось 37, а вот как на складе рассчитать не знаю, буду очень благодарен)
помогите, плиз
Средняя длина очереди:

Среднее время ожидания
в очереди:

Среднее число клиентов
в системе:

Среднее время ожидания
в системе:
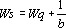
Контрольный
пример 2
Компания «Утиль»
собирает и утилизирует в Мытищах
алюминиевые отходы и стеклянные бутылки.
Водители автомобилей, доставляющие
сырье для вторичной переработки, ожидают
в очереди на разгрузку в среднем 15 мин.
Время простоя водителя и автомобиля
оценивается в 60 тыс. руб. в час.
Новый автоматический компактор может
обслуживать контейнеровозы с постоянным
темпом 12 машин в час (5 мин на одну
машину). Время прибытия контейнеровозов
подчиняется пуассоновскому закону
с параметром z=8 в час.
Если будет использоваться
новый компактор, то амортизационные
затраты составят 3 тыс. руб. на один
контейнеровоз.
Фирма пригласила
студента, который провел следующий
анализ, для оценки целесообразности
использования компактора:
Затраты в настоящее
время: (1/4 ч ожидания)×(60 тыс.
руб./ч)=-15 тыс. руб./поездка.
Новая система:
z=8 автомобилей/ч прибывают;
b=12 автомобилей/ч обслуживается.
Среднее время ожидания
в очереди:

Затраты с новым
компактором: (1/12 ч ожидания)×(60
тыс. руб./ч)=
=5 тыс. руб./поездка.
Доход при новом
оборудовании: 15 (существующая система)–5
(новая система)=10 тыс. руб./поездка.
Амортизационные
затраты: 3 тыс. руб./поездка.
Чистый доход: 7 тыс.
руб./поездка.
Индивидуальное
задание
Решить задачу согласно
вашему варианту, используя модели
массового обслуживания.
Вариант 1
Система банка «Автодор»
позволяет клиенту совершать некоторые
банковские операции, не выходя из машины.
Утром в рабочие дни прибывает в среднем
24 клиента в час. Прибытие клиентов
описывается законом Пуассона.
1. Сколько клиентов в
среднем прибывает за 5 мин?
2. Каковы вероятности
того, что ровно 0, 1, 2, 3 клиента прибудут
за 5 мин?
3. Если в течение 5 мин
прибывает более трех клиентов, то
возникает проблема перегруженности
системы. Какова вероятность возникновения
такой проблемы?
В системе банка
«Автодор» время обслуживания распределено
экспоненциально со средней скоростью
обслуживания 36 клиентов в час.
4. Каковы вероятности
того, что время обслуживания составит:
а) не более 1 мин, б) не более 2 мин, с)
более 2 мин?
5. Определите
следующие характеристики системы:
·
вероятность того, что в системе
нет требований;
·
среднее число требований в
очереди;
·
среднее число требований в
системе;
·
среднее время ожидания;
·
среднее время, которое клиент
проводит в системе;
·
вероятность того, что прибывающему
клиенту придется ждать обслуживания;
·
вероятность того, что в системе
находятся: а) 0 клиентов, б) 3 клиента
и в) более 3 клиентов.
Вариант 2
Справочная университетской
библиотеки получает запросы, поступающие
по пуассоновскому закону со скоростью
в среднем 10 запросов в час. Время
обслуживания распределено экспоненциально,
скорость обслуживания – 12 запросов
в час. Определите:
·
вероятность того, что в системе
нет запросов;
·
среднее число запросов в очереди;
·
среднее время ожидания;
·
среднее время, которое запрос
проводит в системе:
·
вероятность того, что запросу
придется ждать обслуживания.
Вариант 3
Грузовики, прибывающие
на обслуживание в порт, образуют
одноканальную очередь. Их прибытие
распределено по закону Пуассона. Время
погрузки / разгрузки распределено
экспоненциально. Средняя скорость
прибытия – 12 грузовиков в день,
обслуживания – 18 грузовиков в день.
Определите:
·
вероятность того, что в системе
нет грузовиков;
·
среднее число грузовиков в
очереди;
·
среднее время ожидания;
·
вероятность того, что прибывающему
грузовику придется ждать обслуживания.
Вариант 4
Контора принимает
обрабатываемые единственным клерком
заказы, поступающие по закону Пуассона
со средней скоростью 6 заказов в день.
Время на их обработку распределено
экспоненциально со средним уровнем
обслуживания 8 заказов в день. Определите:
·
среднее число заказов в системе;
·
среднее время ожидания начала
обработки заказа клерком;
·
среднее время, которое заказ
проводит в системе.
Вариант 5
В парикмахерской
работает один мастер. Клиенты приходят
со средней скоростью 2,2 человека в час,
средний уровень обслуживания –
5 человек в час. Прибытие клиентов
подчинено закону Пуассона, а время
обслуживания распределено экспоненциально.
Определите:
·
вероятность того, что в системе
нет требований;
·
вероятность того, что один клиент
стрижется и никто другой не ждет;
·
вероятность того, что один клиент
стрижется и еще один ждет:
·
вероятность того, что один клиент
стрижется и еще два ждут;
·
вероятность того, что более двух
клиенток ждут;
·
среднее время ожидания.
Вариант 6
Автосервис решил
нанять нового механика для того, чтобы
он менял старые покрышки на новые. На
это место есть два кандидата. Один из
них имеет ограниченный опыт и может
быть нанят за 7 тыс. руб./ч. Ожидается,
что этот механик сможет обслуживать
трех клиентов в час. Другой механик
более опытен, он в состоянии обслужить
четырех клиентов в час, но его можно
нанять на работу за 10 тыс. руб./ч. Клиенты
прибывают со скоростью 2 человека в час.
Предполагая пуассоновское распределение
времени прибытия и экспоненциальное
распределение продолжительности времени
обслуживания, определите:
·
среднее время, которое клиент
проводит в очереди;
·
среднюю длину очереди;
·
среднее время, которое клиент
проводит в системе обслуживания;
·
среднее число клиентов в системе
обслуживания;
·
вероятность того, что система
обслуживания окажется незанятой при
условии найма одного или другого
механика.
Компания оценивает
издержки по ожиданию клиентами своей
очереди в 15 тыс. руб./ч. Какого механика
следует нанять, чтобы обеспечить меньшие
совокупные издержки? Каковы минимальные
совокупные издержки?
Вариант 7
Фирма «Уют» обеспечивает
своим клиентам помощь в дизайне дома
или офиса. В нормальном режиме каждый
час прибывает в среднем 2,5 клиента.
Единственный консультант по дизайну
отвечает на вопросы клиента и дает
необходимые рекомендации. Он тратит на
каждого посетителя в среднем 10 мин.
Предполагая пуассоновское распределение
времени прибытия и экспоненциальное
распределение продолжительности
обслуживания, определите:
·
среднее время, которое клиент
проводит в очереди;
·
среднюю длину очереди;
·
среднее время, которое клиент
проводит в системе обслуживания;
·
среднее число клиентов в системе
обслуживания;
·
вероятность того, что система
обслуживания окажется незанятой.
Желательно, чтобы
прибывающий клиент не ждал своей очереди
в среднем более 5 мин. Соответствует ли
реальная ситуация данному пожеланию?
Если нет, то что необходимо предпринять?
Предположим, что
консультант способен уменьшить среднее
время, которое он проводит с клиентом,
до 8 мин. Какой стала средняя скорость
обслуживания? Достигнута ли цель теперь?
Вариант 8
«У Петра» – маленький
магазин с одним прилавком. Предположим,
что покупатели прибывают в магазин по
закону Пуассона со средней скоростью
15 покупателей в час. Время обслуживания
распределено экспоненциально, средняя
скорость обслуживания – 20 покупателей
в час. Рассчитайте:
·
среднее время, которое покупатель
проводит в очереди,
·
среднюю длину очереди,
·
среднее время, которое покупатель
проводит в магазине,
·
среднее число покупателей в
магазине,
·
вероятность того, что в магазине
не окажется покупателей.
Вариант 9
В верхнем течении
Волги построена новая станция по
обслуживанию речных судов. Судно может
остановиться в новом доке для заправки
и ремонта. Суда прибывают по закону
Пуассона со средней скоростью 5 судов
в час. Время обслуживания распределено
экспоненциально со средней скоростью
обслуживания10 судов в час.
1. Какова вероятность
того, что док будет пуст?
2. Каково среднее число
судов в очереди?
3. Каково среднее время
ожидания обслуживания?
4. Каково среднее время
пребывания в доке?
Вариант
10
Пациенты прибывают к
дантисту со средней скоростью 2,8 человека
в час. Дантист в среднем способен
обслужить 3 человека в час. Наблюдения
показывают, что в среднем пациент ждет
30 мин.
Чему равны средние
скорости прибытия и обслуживания,
выраженные в пациентах в минуту?
Какова средняя длина
очереди?
Вариант
11
Механики компании
«Автосервис» прибывают на главный склад
за запчастями со средней скоростью
4 механика в 1 мин. Сейчас на складе
один работник. Каждый механик в среднем
ждет обслуживания 4 мин. Найдите:
·
среднее число клиентов в системе;
·
среднее время обслуживания
одного клиента в системе;
·
среднее число клиентов в очереди.
Вариант 12
Офисный ксерокс
используют 5 служащих. Среднее время
между двумя моментами его использования
для каждого из служащих равно 40 мин.
В среднем служащий занимает ксерокс на
5 мин. Используя модель М/М/1 с
ограниченным множеством требований,
определите:
·
вероятность того, что ксерокс
простаивает;
·
среднее число служащих в очереди;
·
среднее число служащих в комнате,
где стоит ксерокс;
·
среднее время ожидания;
·
среднее время нахождения в
комнате с ксероксом.
Сколько времени за
восьмичасовой рабочий день тратит
служащий на данную операцию?
Стоит ли компании
приобретать второй ксерокс? Ответ
обосновать.
Вариант
13
В распоряжении магазина
находится 10 грузовиков. Грузовики
прибывают в магазин в случайном
порядке в течение дня для погрузки / разгрузки.
Каждый грузовик прибывает на обслуживание
дважды за 8‑часовой рабочий день.
Средняя скорость обслуживания –
4 грузовика в час. Модель прибытия
требований – пуассоновская, модель
времени обслуживания –
экспоненциальная. Определите:
·
вероятность того, что ни один
грузовик не ожидает погрузки /
разгрузки;
·
среднее число грузовиков в
очереди;
·
среднее число грузовиков у
магазина (грузовики в очереди и на
погрузке / разгрузке);
·
среднее время ожидания.
Каковы часовые издержки
по функционированию системы, если в
1 час издержки на каждый грузовик
равны 50 тыс. руб., а на работы с грузовиками –
30 тыс. руб.?
Вариант
14
Клиенты приходят к
парикмахеру со средней скоростью
2,3 человека в час. Парикмахер в
среднем способен обслужить 3 человека
в час. Наблюдения показывают, что в
среднем клиент ждет 25 мин.
Чему равны средние
скорости прибытия и обслуживания,
выраженные в клиентах в минуту?
Какова средняя длина
очереди?
Вариант
15
Офисный принтер
используют 10 служащих. Среднее время
между двумя моментами его использования
для каждого из служащих равно 20 мин.
В среднем служащий занимает ксерокс на
5 мин. Используя модель М/М/1 с
ограниченным множеством требований,
определите:
·
вероятность того, что принтер
простаивает;
·
среднее число служащих в очереди;
·
среднее число служащих в комнате,
где стоит принтер;
·
среднее время ожидания;
·
среднее время пребывания в
комнате с принтером.
Сколько времени за
семичасовой рабочий день тратит служащий
на данную операцию?
Стоит ли компании
приобретать второй принтер? Объясните.
Контрольные
вопросы
1. Что такое одноканальная
система?
2. Что такое однофазовая
система?
3. Что такое очередь?
4. Что такое распределение
времени обслуживания?
5. Что означает и как
определяется среднее время в очереди?
6. Что означает и как
определяется среднее время в системе?
7. Что означает и как
определяется среднее число клиентов в
очереди?
8. Что означает и как
определяется среднее число клиентов в
системе?
9. Что означает и как
определяется средний темп поступления
заявок?
10. Что означает и как
определяется средняя длина очереди?
Лабораторная
работа № 8 Модели управления запасами
Цель работы: освоить
и закрепить практические навыки по
использованию моделей управления
запасами.
Краткие теоретические сведения 8.1. Общие
определения
Запасаминазывается
любой ресурс на складе, который
используется для удовлетворения будущих
нужд. Примерами запасов могут служить
полуфабрикаты, готовые изделия, материалы,
различные товары, а также такие
специфические товары, как денежная
наличность, находящаяся в хранилище.
Большинство организаций имеют примерно
один тип системы планирования и контроля
запасов. В банке используются методы
контроля за количеством наличности, в
больнице применяются методы контроля
поставки различных медицинских
препаратов.
Существует много
причин, побуждающих организации создавать
запасы.
Существует проблема
классификации имеющихся в наличии
запасов. Для решения этой задачи
используется методика административного
наблюдения. Цель ее заключается в
определении той части запасов предприятия,
которая требует наибольшего внимания
со стороны отдела снабжения. Для этого
каждый компонент запасов рассматривается
по двум параметрам: а) его доля в общем
количестве запасов предприятия; б) его
доля в общей стоимости запасов предприятия.
Методика 20/80–
в соответствии с этой методикой компоненты
запаса, составляющие 20% его общего
количества и 80% его общей стоимости,
должны отслеживаться отделом снабжения
более внимательно.
Методика ABC:в
рамках этой методики запасы, имеющиеся
в распоряжении предприятия, разделяются
на три группы: группу А (10% общего
количества запасов и 65% его стоимости);
группу В (25% общего количества запасов
и 25% его стоимости); группу С (65% общего
количества запасов и около 10% его
стоимости).
Необходимо отметить,
что классификация запасов может быть
основана не только на показателях доли
в общей стоимости и в общем количестве.
Преимущества методики деления видов
запасов на классы заключаются в
возможности выбора порядка контроля и
управления для каждого из них.
Рассмотрим определяющие
понятия теории управления запасами.
Издержки выполнения
заказа(издержки заказа) – накладные
расходы, связанные с реализацией заказа.
В промышленности такими издержками
являются затраты на подготовительно-заготовочные
операции.
Издержки хранения–
расходы, связанные с физическим
содержанием товаров на складе, плюс
возможные проценты на капитал, вложенный
в запасы. Обычно они выражаются или в
абсолютных единицах, или в процентах
от закупочной цены и связываются с
определенным промежутком времени.
Упущенная прибыль–
издержки, связанные с неудовлетворенным
спросом, возникающим в результате
отсутствия продукта на складе.
Совокупные издержки
за периодпредставляют собой сумму
издержек заказа, издержек хранения и
упущенного дохода. Иногда к ним
прибавляются издержки на покупку
товаров.
Срок выполнения
заказа– срок между заказом и его
выполнением. Точка восстановления –
уровень запаса, при котором делается
новый заказ.
8.2. Краткая характеристика моделей
управления запасами 1. Модель оптимального
размера заказа
Предпосылки: 1) темп
спроса на товар известен и постоянен;
2) получение заказа мгновенно;
3) отсутствуют количественные скидки
при закупке больших партий товара;
4) единственные меняющиеся параметры –
издержки заказа и хранения; 5) исключается
дефицит в случае своевременного
заказа.
Исходные данные: темп
спроса, издержки заказа и хранения.
Результат: оптимальный
размер заказа, время между заказами и
их количество за период.
2. Модель
оптимального размера заказа в
предположении, что получение заказа не
мгновенно
Следовательно, нужно
найти объем запасов, при котором
необходимо делать новый заказ.
Исходные данные: темп
спроса, издержки заказа и хранения,
время выполнения заказа.
Результат: оптимальный
размер заказа, время между заказами,
точка восстановления запаса.
3. Модель
оптимального размера заказа в
предположении, что допускается дефицит
продукта и связанная с ним упущенная
прибыль
Необходимо найти точку
восстановления.
Исходные данные: темп
спроса, издержки заказа и хранения,
упущенная прибыль.
Результат: оптимальный
размер заказа, время между заказами,
точка восстановления запаса.
4. Модель
с учетом производства (в сочетании с
условиями 1–3)
Необходимо рассматривать
уровень ежедневного производства и
уровень ежедневного спроса.
Исходные данные: темп
спроса, издержки заказа, хранения и
упущенная прибыль, темп производства.
Результат: оптимальный
уровень запасов (точка восстановления
запаса).
5. Модель
с количественными скидками
Появляется возможность
количественных скидок в зависимости
от размера заказа. Рассматривается
зависимость издержек хранения от цены
товара. Оптимальный уровень заказа
определяется исходя из условия минимизации
общих издержек для каждого вида скидок.
Модели
типа 1–5 с вероятностным распределением
спроса и времени выполнения заказа
Вместо предпосылки о
постоянстве и детерминированности
спроса на товар используется более
реалистичный подход о предполагаемой
известности распределения темпа спроса
и времени выполнения заказа.
Рассмотрим подробнее
модели с фиксированным размером заказа:
Модель 1. Модель
наиболее экономичного размера заказа.
Заказ, пополняющий запасы, поступает
как одна партия. Уровень запасов убывает
с постоянной интенсивностью, пока не
достигает нуля. В этой точке поступает
заказ, размер которого равен Q, и уровень
запасов восстанавливается до
максимального значения. При этом
оптимальным решением задачи будет тот
размер заказа, при котором минимизируются
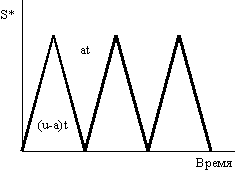
общие издержки за период (рис. 8.1).
Рис. 8.1. Модель 1. Модель
наиболее экономичного размера заказа
Пусть Q – размер
заказа; Т – протяженность периода
планирования; D – величина спроса за
период планирования; d – величина
спроса в единицу времени; К – издержки
заказа; Н – удельные издержки хранения
за период; h – удельные издержки
хранения в единицу времени. Тогда:
(D/Q)K – совокупные
издержки заказа;
(Q/2)H – совокупные
издержки хранения;
d=D/T; h=H/T;
Q*=(2dK/h)1/2(2DK/H)1/2–
оптимальный размер заказа;
N=D/Q* – оптимальное
число заказов за период;
t*=Q*/d=T/N – время цикла
(оптимальное время между заказами).
Модель 2.Введем
предположение о том, что заказ может
быть получен не мгновенно, а с течением
времени. Тогда нам необходимо заранее
делать заказ, чтобы в нужное время иметь
достаточное количество товара на складе.
Следовательно, нам необходимо найти
тот уровень запасов, при котором делается
новый заказ. Этот уровень называется
точкой восстановления R. Пусть L –
время выполнения заказа. Тогда R –
величина спроса в единицу времени,
умноженная на время выполнения заказа
(d×L). Другие характеристики
системы определяются так же, как и в
модели 1. Модель иллюстрируется на
рис. 8.2.
Рис. 8.2. Модель 2
Контрольный
пример 1
Андрей является
торговым агентом компании «VOLVO» и
занимается продажей последней модели
этой марки автомобиля.
Годовой спрос оценивается
в 4000 ед. Цена каждого автомобиля равна
90 млн руб., а годовые издержки
хранения составляют 10% от цены самого
автомобиля.
Андрей произвел анализ
издержек заказа и понял, что средние
издержки заказа составляют 25 млн руб.
на заказ. Время выполнения заказа равно
восьми дням. В течение этого времени
ежедневный спрос на автомобили равен
20.
Необходимо в процессе
решения данного примера ответить на
следующие вопросы:
1. Чему равен оптимальный
размер заказа?
2. Чему равна точка
восстановления?
3. Каковы совокупные
издержки?
4. Каково оптимальное
количество заказов в год?
5. Каково оптимальное
время между двумя заказами, если
предположить, что количество рабочих
дней в году равно 200?
Ниже приведено описание
исходных данных и результаты решения
контрольного примера с использованием
условных обозначений.
Исходные данные:
величина спроса за
год D=4000;
издержки заказа К=25;
издержки хранения
=9/200;
цена за единицу с=90;
время выполнения
заказа L=8;
ежедневный спрос d=20;
число рабочих дней
Т=200.
Решение:
оптимальный размер
заказа Q*=149;
точка восстановления
R=160–149=11;
число заказов за год
N=26,83;
совокупные издержки
С=1341;
стоимость продаж
=360 000;
число дней между
заказами t=7,45.
Модель 3.Модель
оптимального размера заказа в
предположении, что допускается дефицит
продукта и связанная с ним упущенная
прибыль (рис. 8.3).
Рис. 8.3. Модель 3
Пусть р – упущенная
прибыль в единицу времени, возникающая
в результате дефицита одной единицы
продукта; Р – упущенная прибыль за
период, возникающая в результате дефицита
одной единицы продукта.
Тогда:
Q*=(2dK/h)1/2×((р+h)/р)1/2=(2DK/H)1/2×((Р+Н)/P)1/2–
оптимальный размер заказа;
S*=(2dK/h)1/2×(р/(h+р))1/2=(2DK/H)1/2×(P/(H+P))1/2–
максимальный размер запаса; R=Q*–S* –
максимальный дефицит.
Модель 4.Модель
производства и распределения. В предыдущей
модели мы допускали, что пополнение
запаса происходит единовременно. Но в
некоторых случаях, особенно в промышленном
производстве, для комплектования партии
товаров требуется значительное время,
и производство товаров для пополнения
запасов происходит одновременно с
удовлетворением спроса. Такой случай
показан на рис. 8.4.
Рис. 8.4. Модель 4
Спрос и производство
являются частью цикла восстановления
запасов. Пусть u – уровень производства
в единицу времени, К – фиксированные
издержки производства.
Тогда:
совокупные издержки
хранения = (средний уровень
запасов)×Н=
=Q/2[1-d/u] Н;
средний уровень запасов
= (максимальный уровень запасов)/2;
максимальный уровень
запасов =u×t–d×t=Q(l–d/u);
время выполнения
заказа t=Q/u;
издержки заказа
=(D/Q)×К;
оптимальный размер
заказа Q*=(2dK/h×[(l-(d/u)])1/2=(2DK/H[(l-(d/u)])1/2;
максимальный уровень
запасов S*=Q*[(l-(d/u)].
Модель 5. Модель с
количественными скидками. Для увеличения
объема продаж компании часто предлагают
количественные скидки своим
покупателям.
Количественная скидка –
сокращенная цена на товар в случае
покупки большого количества этого
товара. Типичные примеры количественных
скидок приведены в табл. 8.1.
Таблица 8.1
|
Варианты скидок |
1 |
2 |
3 |
|
Количество, при котором |
от 0 до 999 |
от 1000 до 1999 |
от 2000 и выше |
|
Размер скидки, % |
0 |
3 |
5 |
|
Цена со скидкой |
5 |
4,8 |
4,75 |
Пусть I – доля
издержек хранения в цене продукта с.
Тогда h=(I×c)
и Q*=(2dK/(I×c))1/2–
оптимальный размер заказа.
Контрольный пример 2
Рассмотрим пример,
объясняющий принцип принятия решения
в условиях скидки. Магазин «Медвежонок»
продает игрушечные гоночные машинки.
Эта фирма имеет таблицу скидок на машинки
в случае покупок их в определенном
количестве (табл. 8.2). Издержки заказа
составляют 49 тыс. руб. Годовой спрос на
машинки равен 5000. Годовые издержки
хранения в отношении к цене составляют
20%, или 0,2. Необходимо найти размер заказа,
минимизирующий общие издержки.
Решение
Рассчитаем оптимальный
размер заказа для каждого вида скидок,
т.е. Q1*, Q2* и Q3*, и получим Q1*=700; Q2*=714; Q3*=718.
Так как Q1* – величина
между 0 и 999, то ее можно оставить прежней.
Q2* меньше количества, необходимого для
получения скидки, следовательно, его
значение необходимо принять равным
1000 единиц. Аналогично Q3* берем равным
2000 единиц. Получим Q1*=700; Q2*=1000; Q3*=2000.
Далее необходимо
рассчитать общие издержки для каждого
размера заказа и вида скидок, а затем
выбрать наименьшее значение.
Рассмотрим следующую
таблицу:
Таблица 8.2
|
Вид скидки |
1 |
1 |
3 |
|
Цена |
5 |
4,8 |
4,75 |
|
Размер заказа |
700 |
1000 |
2000 |
|
Цена на товар за год |
25 000 |
24 000 |
23 750 |
|
Годовые издержки заказа |
350 |
245 |
122,5 |
|
Годовые издержки хранения |
350 |
480 |
950 |
|
Общие годовые издержки |
25 700 |
24 725 |
24 822,5 |
Выберем тот размер
заказа, который минимизирует общие
годовые издержки. Из таблицы видно, что
заказ в размере 1000 игрушечных гоночных
машинок будет минимизировать совокупные
издержки.
Индивидуальное
задание
Решить задачу согласно
вашему варианту, используя модели
управления запасами.
Вариант 1
Господин Бобров
приобретает в течение года 1500 телевизоров
для розничной продажи в своем магазине.
Издержки хранения каждого телевизора
равны 45 тыс. руб. в год. Издержки заказа –
150 тыс. руб. Количество рабочих дней в
году равно 300, время выполнения заказа –
6 дней. Необходимо найти:
·
оптимальный размер заказа;
·
годовые издержки заказа;
·
точку восстановления запаса.
Вариант 2
Анна Васильева из
компании «Сюрприз» продает 400 водяных
кроватей в год, причем издержки хранения
равны 1 тыс. руб. за кровать в день и
издержки заказа – 40 тыс. руб.
Количество рабочих дней равно 250 и время
выполнения заказа – 6 дней. Каков
оптимальный размер заказа? Чему равна
точка восстановления запаса? Каков
оптимальный размер заказа, если издержки
хранения равны 1,5 тыс. руб.?
Вариант 3
Мекки Мессер является
владельцем маленькой компании, которая
выпускает электрические ножи. В
среднем Мекки может производить
150 ножей в день. Дневной спрос на
ножи примерно равен 40. Фиксированные
издержки производства равны 100 тыс.
руб., издержки хранения – 8 тыс.
руб. за нож в год. Какой максимальный
заказ следует иметь на складе?
Вариант 4
Компания «Веселые
ребята» закупает у завода-изготовителя
лобовые стекла грузовых автомобилей
«Урал» для розничной продажи. В год, за
200 рабочих дней, реализуется около 10 000
стекол. Издержки заказа для компании
составляют 400 тыс. руб., ежедневные
издержки хранения одного стекла –
6 тыс. руб. Чему равен оптимальный размер
заказа? Каковы минимальные годовые
совокупные издержки?
Вариант 5
Годовой заказ на тостер
«Слава» для салона Марии Мягковой равен
3000 единиц, или 10 в день. Издержки
заказа равны 25 тыс. руб. издержки
хранения – 0,4 тыс. руб. в день. Так как
тостер «Слава» является очень популярным
среди покупателей, то в случае отсутствия
товара покупатели обычно согласны
подождать, пока не подойдет следующий
заказ. Однако издержки, связанные с
дефицитом, равны 0,75 тыс. руб. за тостер
в день. Сколько тостеров будет заказывать
Мария? Каков максимальный дефицит? Чему
равны совокупные издержки?
Вариант 6
Магазин «Природа»
пользуется популярностью у покупателей
благодаря широкому ассортименту
экологически чистых продуктов. Большинство
покупателей не отказываются от услуг
магазина даже в том случае, когда
интересующий их товар отсутствует в
продаже. Они оставляют заказ на товар
и ждут, когда поступит новая партия.
Сыр «Витаум» – не
самый популярный из всего набора товаров,
но администратор магазина регулярно
заказывает этот продукт. Годовой спрос
на «Витаум» составляет 500 головок сыра.
Издержки заказа – 40 тыс. руб. за
заказ. Издержки хранения – 5 тыс.
руб. в год. Упущенная прибыль вследствие
дефицита составляет 100 тыс. руб. за
год на одну головку сыра.
Сколько головок сыра
следует заказывать, чтобы не допустить
дефицита и иметь при этом минимальные
общие издержки?
Сколько сыра следует
заказывать, если допустить возможность
дефицита?
Чему равна точка
восстановления запаса, если время
выполнения заказа составляет 10 дней и
число рабочих дней в году 250?
Чему равен максимальный
размер дефицита?
Вариант 7
Компания «Химпласт»
предлагает следующие скидки для линолеума
размером 2´3 м (табл. 8.3).
Таблица 8.3
|
Размер заказа |
9 кусков или менее |
10–50 кусков |
50 кусков и более |
|
Цена 1 куска |
18 тыс. руб. |
17,5 тыс. руб. |
17,25 тыс. руб. |
Магазин «Все для дома»
заказывает у компании линолеум. Издержки
заказа равны 45 тыс. руб. Годовые издержки
хранения равны 50% от цены. Годовой спрос
на линолеум в магазине составляет
100 кусков. Какое количество необходимо
приобрести?
Вариант 8
Мебельный салон
«Антика» продает в год около 1000 спальных
гарнитуров по цене 50 млн руб. Размещение
одного заказа на поставку гарнитуров
обходится в 40 млн руб. Годовая стоимость
хранения гарнитура составляет 25% его
цены. Салон может получить 3%-ную скидку
у поставщика, если размер заказа составит
не менее 200 гарнитуров. Следует ли салону
заказывать 200 или более гарнитуров и
пользоваться скидкой?
Вариант 9
Обычная оптовая цена
аудиоколонок для автомагнитолы –
20 тыс. руб. В случае заказа от 75 до 90
колонок цена сокращается до 18,5 тыс.
руб. При заказе более 100 колонок цена
снижается до 15,75 тыс. руб. Издержки
заказа для компании «Эхо», являющейся
производителем колонок, равны 10 тыс.
руб., годовые издержки хранения – 5%
от стоимости колонки. Ежедневная величина
спроса в течение 250 дней реализации в
году – 25 колонок. Каков оптимальный
размер заказа и чему равны минимальные
средние ежедневные издержки?
Вариант
10
Компания «Интегро»
продает в год около 2000 шкафов-купе по
цене 40 тыс. руб. Размещение одного
заказа на поставку шкафов-купе обходится
в 30 тыс. руб. Годовая стоимость хранения
гарнитура составляет 20% его цены. Компания
может получить 5%-ную скидку у поставщика,
если размер заказа составит не менее
300 гарнитуров. Следует ли салону
заказывать 300 или более гарнитуров и
пользоваться скидкой?
Вариант
11
Компания «Люкс»
предлагает следующие скидки для обоев
(табл. 8.4).
Таблица 8.4
|
Размер заказа |
10 метров и менее |
10–100 метров |
Более 100 метров |
|
Цена 1 метра |
300 руб. |
250 руб. |
210 руб. |
Магазин «Уют» заказывает
у компании обои. Издержки заказа равны
50 тыс. руб. Годовые издержки хранения
равны 40% от цены. Годовой спрос на линолеум
в магазине составляет 2000 метров. Какое
количество необходимо приобрести?
Вариант 12
Петр Иванович из
компании «Уют» продает 600 спален в год,
причем издержки хранения равны 500 руб.
за кровать в день и издержки заказа –
50 тыс. руб. Количество рабочих дней равно
250 и время выполнения заказа – 5 дней.
Каков оптимальный размер заказа? Чему
равна точка восстановления запаса?
Каков оптимальный размер заказа, если
издержки хранения равны 1 тыс. руб.?
Вариант
13
Иванов Иван является
владельцем компании, которая изготовляет
игрушки. В среднем компания может
производить 50 игрушек в день. Дневной
спрос на игрушки примерно равен 40.
Фиксированные издержки производства
равны 100 тыс. руб., издержки хранения –
20 тыс. руб. за игрушку в год. Какой
максимальный заказ следует иметь на
складе?
Вариант
14
Иван Федорович
приобретает в течение года
300 видеомагнитофонов для розничной
продажи в своем магазине. Издержки
хранения каждого магнитофона равны
20 тыс. руб. в год. Издержки заказа –
100 тыс. руб. Количество рабочих дней
в году равно 300, время выполнения заказа –
5 дней. Необходимо найти:
·
оптимальный размер заказа;
·
годовые издержки заказа;
·
точку восстановления запаса.
Вариант
15
Фирма приобретает в
течение года 1000 компьютеров для розничной
продажи. Издержки хранения каждого
компьютера равны 25 тыс. руб. в год.
Издержки заказа – 300 тыс. руб.
Количество рабочих дней в году равно
290, время выполнения заказа – 10 дней.
Необходимо найти:
·
оптимальный размер заказа;
·
годовые издержки заказа;
·
точку восстановления запаса.
Контрольные
вопросы
1. Что такое время
выполнения заказа?
2. Что такое время
цикла?
3. Что такое запас?
4. Что такое издержки
заказа?
5. Что такое издержки
хранения?
6. Что такое точка
восстановления?
7. Что такое упущенная
прибыль?
8. Какие модели управления
запасами вы знаете?
9. Опишите модель
оптимального размера заказа.
10. Опишите модель
заказа с количественными ссылками.

Лабораторная работа
Модели управления запасами
Цель работы: освоить и закрепить практические навыки по использованию моделей управления запасами.
Краткие теоретические сведения
6.1. Общие определения
Запасами называется любой ресурс на складе, который используется для удовлетворения будущих нужд. Примерами запасов могут служить полуфабрикаты, готовые изделия, материалы, различные товары, а также такие специфические товары, как денежная наличность, находящаяся в хранилище. Большинство организаций имеют примерно один тип системы планирования и контроля запасов. В банке используются методы контроля за количеством наличности, в больнице применяются методы контроля поставки различных медицинских препаратов.
Существуют многие причины, побуждающие организации создавать запасы.
Существует проблема классификации имеющихся в наличии запасов. Для решения этой задачи используется методика административного наблюдения. Цель ее заключается в определении той части запасов предприятия, которая требует наибольшего внимания со стороны отдела снабжения. Для этого каждый компонент запасов рассматривается по двум параметрам: а) его доля в общем количестве запасов предприятия; б) его доля в общей стоимости запасов предприятия.
Методика 20/80. в соответствии с этой методикой компоненты запаса, составляющие 20% его общего количества и 80% его общей стоимости, должны отслеживаться отделом снабжения более внимательно.
Методика ABC: в рамках этой методики запасы, имеющиеся в распоряжении предприятия, разделяются на три группы: группу А (10% общего количества запасов и 65% его стоимости); группу В (25% общего количества запасов и 25% его стоимости); группу С (65% общего количества запасов и около 10% его стоимости).
Необходимо отметить, что классификация запасов может быть основана не только на показателях доли в общей стоимости и в общем количестве. Преимущества методики деления видов запасов на классы заключаются в возможности выбора порядка контроля и управления для каждого из них.
Рассмотрим определяющие понятия теории управления запасами.
Издержки выполнения заказа (издержки заказа) — накладные расходы, связанные с реализацией заказа. В промышленности такими издержками являются затраты на подготовительно-заготовочные операции.
Издержки хранения — расходы, связанные с физическим содержанием товаров на складе, плюс возможные проценты на капитал, вложенный в запасы. Обычно они выражаются или в абсолютных единицах, или в процентах от закупочной цены и связываются с определенным промежутком времени.
Упущенная прибыль — издержки, связанные с неудовлетворенным спросом, возникающим в результате отсутствия продукта на складе.
Совокупные издержки за период представляют собой сумму издержек заказа, издержек хранения и упущенною дохода. Иногда к ним прибавляются издержки на покупку товаров.
Срок выполнения заказа — срок между заказом и его выполнением. Точка восстановления — уровень запаса, при котором делается новый заказ.
6.2. Краткая характеристика моделей управления запасами
1. Модель оптимального размера заказа
Предпосылки:
1)темп спроса на товар известен и постоянен;
2) получение заказа мгновенно;
3) отсутствуют количественные скидки при закупке больших партий товара;
4) единственные меняющиеся параметры — издержки заказа и хранения;
5) исключается дефицит в случае своевременного заказа.
Исходные данные: темп спроса, издержки заказа и хранения.
Результат: оптимальный размер заказа, время между заказами и их количество за период.
2. Модель оптимального размера заказа в предположении, что получение заказа не мгновенно
Следовательно, нужно найти объем запасов, при котором необходимо делать новый заказ.
Исходные данные: темп спроса, издержки заказа и хранения, время выполнения заказа.
Результат: оптимальный размер заказа, время между заказами, точка восстановления запаса.
3. Модель оптимального размера заказа в предположении, что допускается дефицит продукта и связанная с ним упущенная прибыль
Необходимо найти точку восстановления.
Исходные данные: темп спроса, издержки заказа и хранения, упущенная прибыль.
Результат: оптимальный размер заказа, время между заказами. точка восстановления запаса.
4. Модель с учетом производства
(в сочетании с условиями 1-3)
Необходимо рассматривать уровень ежедневного производства и уровень ежедневного спроса.
Исходные данные: темп спроса, издержки заказа, хранения и упущенная прибыль, темп производства.
Результат: оптимальный уровень запасов (точка восстановления запаса).
5. Модель с количественными скидками
Появляется возможность количественных скидок в зависимости от размера заказа. Рассматривается зависимость издержек хранения от цены товара. Оптимальный уровень заказа определяется исходя из условия минимизации общих издержек для каждого вида скидок.
Модели типа 1-5 с вероятностным распределением спроса и времени выполнения заказа
Вместо предпосылки о постоянстве и детерминированности спроса на товар используется более реалистичный подход о предполагаемой известности распределения темпа спроса и времени выполнения заказа.
Рассмотрим подробнее модели с фиксированным размером заказа.
Модель 1. Наиболее экономичного размера заказа. Заказ, пополняющий запасы, поступает как одна партия. Уровень запасов убывает с постоянной интенсивностью пока не достигает нуля. В этой точке поступает заказ, размер которого равен Q, и уровень запасов восстанавливается до максимального значения. При этом оптимальным решением задачи будет тот размер заказа, при котором минимизируются общие издержки за период (рис.6.1).
Пусть Q — размер заказа; Т — протяженность периода планирования; D — величина спроса за период планирования; d — величина спроса в единицу времени; К — издержки заказа; Н — удельные издержки хранения за период; h — удельные издержки хранения в единицу времени. Тогда:
(D/Q)K — совокупные издержки заказа;
(Q/2)H — совокупные издержки хранения;
d = D/T; h = H/T;
Q* =(2dK/h)1/2 (2DK/H)1/2 — оптимальный размер заказа;
N = D/Q* — оптимальное число заказов за период;
t* = Q*/d = T/N — время цикла (оптимальное время между заказами).
Модель 2. Введем предположение о том, что заказ может быть получен не мгновенно, а с течением времени. Тогда нам необходимо заранее делать заказ, чтобы в нужное время иметь достаточное количество товара на складе. Следовательно, нам необходимо найти тот уровень запасов, при котором делается новый заказ. Этот уровень называется точкой восстановления R. Пусть L — время выполнения заказа. Тогда R = величина спроса в единицу времени, умноженная на время выполнения заказа = d L. Другие характеристики системы определяются так же, как и в модели 1. Модель иллюстрируется рис.6.2.
Контрольный пример 1
Андрей является торговым агентом компании VOLVO и занимается продажей последней модели этой марки автомобиля.
Годовой спрос оценивается в 4000 ед. Цена каждого автомобиля равна 90 млн. р., а годовые издержки хранения составляют 10% от цены самого автомобиля.
Андрей произвел анализ издержек заказа и понял, что средние издержки заказа составляют 25 млн. р. на заказ. Время выполнения заказа равно восьми дням. В течение этого времени ежедневный спрос на автомобили равен 20.
Необходимо в процессе решения данного примера ответить на следующие вопросы:
1. Чему равен оптимальный размер заказа?
2. Чему равна точка восстановления?
3. Каковы совокупные издержки?
4. Каково оптимальное количество заказов в год?
5. Каково оптимальное время между двумя заказами, если предположить, что количество рабочих дней в году равно 200?
Ниже приведено описание исходных данных и результаты решения контрольного примера с использованием условных обозначений:
Исходные данные:
величина спроса за год D=4000;
издержки заказа К = 25;
издержки хранения = 9/200;
цена за единицу с = 90;
время выполнения заказа L=8;
ежедневный спрос d= 20;
число рабочих дней Т = 200.
Решение:
оптимальный размер заказа Q* = 149;
точка восстановления R = 160 — 149 = 11;
число заказов за год N = 26,83;
совокупные издержки С = 1341;
стоимость продаж = 360000;
число дней между заказами t = 7,45.
Модель 3 оптимального размера заказа в предположении, что допускается дефицит продукта и связанная с ним упущенная прибыль (рис. 6.3).
Пусть р — упущенная прибыль в единицу времени, возникающая в результате дефицита одной единицы продукта; Р — упущенная прибыль за период, возникающая в результате дефицита одной единицы продукта.
Тогда:Q* = (2dK/h)1/2 x ((р+h)/р)1/2=(2DK/H)1/2 х ((Р+Н)/P)1/2 — оптимальный размер заказа; S* = (2dK/h)1/2 x (р/(h+р))1/2 =(2DK/H)1/2 x (P/(H+P))1/2 — максимальный размер запаса;R = Q*- S* — максимальный дефицит.
Модель. 4 производства и распределения. В предыдущей модели мы допускали, что пополнение запаса происходит единовременно. Но в некоторых случаях, особенно в промышленном производстве, для комплектования партии товаров требуется значительное время и производство товаров для пополнения запасов происходит одновременно с удовлетворением спроса. Такой случай показан на рис.6.4.
Спрос и производство являются частью цикла восстановления запасов. Пусть u — уровень производства в единицу времени, К — фиксированные издержки производства.
Тогда:
совокупные издержки хранения = (средний уровень запасов) х Н = Q/2[1-d/u] Н;
средний уровень запасов = (максимальный уровень запасов)/2;
максимальный уровень запасов = u t — d t = Q(l — d/u);
время выполнения заказа t = Q/u;
издержки заказа = (D/Q) К;
оптимальный размер заказа Q* = (2dK/h [(l-(d/u)])1/2 = (2DK/H[(l-(d/u)])1/2;
максимальный уровень запасов S* = Q*[(l-(d/u)].
Модель 5. Модель с количественными скидками. Для увеличения объема продаж компании часто предлагают количественные скидки своим покупателям.
Количественная скидка — сокращенная цена на товар в случае покупки большого количества этого товара. Типичные примеры количественных скидок приведены в табл.8.1.
Таблица 6.1
|
Варианты скидок |
1 |
2 |
3 |
|
Количество, при котором делается скидка |
от 0 до 999 |
от 1000 до 1999 |
от 2000 и выше |
|
Размер скидки, % |
0 |
3 |
5 |
|
Цена со скидкой |
5 |
4,8 |
4,75 |
Пусть I — доля издержек хранения в цене продукта с.
Тогда h = (I x c) и Q* = ( 2dK/(I x c))1/2 — оптимальный размер заказа.
Контрольный пример 2
Рассмотрим пример, объясняющий принцип принятия решения в условиях скидки. Магазин «Медвежонок» продает игрушечные гоночные машинки. Эта фирма имеет таблицу скидок на машинки в случае покупок их в определенном количестве (табл. 6.1). Издержки заказа составляют 49 тыс. р. Годовой спрос на машинки равен 5000. Годовые издержки хранения в отношении к цене составляют 20%, или 0,2. Необходимо найти размер заказа, минимизирующий общие издержки.
Решение
Рассчитаем оптимальный размер заказа для каждого вида скидок, т.е. Q1*, Q2* и Q3*. и получим Q1* = 700; Q2* = 714; Q3* = 718.
Так как Q1* — величина между 0 и 999, то ее можно оставить прежней. Q2* меньше количества, необходимого для получения скидки, следовательно, его значение необходимо принять равным 1000 единиц. Аналогично Q3* берем равным 2000 единиц. Получим Q1* = 700; Q2* = 1000; Q3* = 2000.
Далее необходимо рассчитать общие издержки для каждого размера заказа и вида скидок, а затем выбрать наименьшее значение.
Рассмотрим следующую таблицу:
Таблица 6.2
|
Вид скидки |
1 |
1 |
3 |
|
Цена |
5 |
4,8 |
4,75 |
|
Размер заказа |
700 |
1000 |
2000 |
|
Цена на товар за год |
25000 |
24000 |
23750 |
|
Годовые издержки заказа |
350 |
245 |
122,5 |
Годовые издержки хранения |
350 |
480 |
950 |
|
Общие годовые издержки |
25700 |
24725 |
24822,5 |
Выберем тот размер заказа, который минимизирует общие годовые издержки. Из таблицы видно, что заказ в размере 1000 игрушечных гоночных машинок будет минимизировать совокупные издержки.
Индивидуальное задание
Решить задачу, согласно вашему варианту, используя модели управления запасами.
Вариант 1
Господин Бобров приобретает в течение года 1500 телевизоров для розничной продажи в своем магазине. Издержки хранения каждого телевизора равны 45 тыс. р. в год. Издержки заказа — 150 тыс. р. Количество рабочих дней в году равно 300, время выполнения заказа — 6 дней. Необходимо найти:
-
оптимальный размер заказа;
-
годовые издержки заказа;
-
точку восстановления запаса.
Вариант 2
Анна Васильева из компании «Сюрприз» продает 400 водяных кроватей в год, причем издержки хранения равны 1 тыс. р. за кровать в день и издержки заказа — 40 тыс. р. Количество рабочих дней равно 250 и время выполнения заказа — 6 дней. Каков оптимальный размер заказа? Чему равна точка восстановления запаса? Каков оптимальный размер заказа, если издержки хранения равны 1,5 тыс. р.?
Вариант 3
Мекки Мессер является владельцем маленькой компании, которая выпускает электрические ножи. В среднем Мекки может производить 150 ножей в день. Дневной спрос на ножи примерно равен 40. Фиксированные издержки производства равны 100 тыс. р., издержки хранения — 8 тыс. р. за нож в год. Какой максимальный заказ следует иметь на складе?
Вариант 4
Компания «Веселые ребята» закупает у завода-изготовителя лобовые стекла грузовых автомобилей «Урал» для розничной продажи. В год, за 200 рабочих дней, реализуется около 10 000 стекол. Издержки заказа для компании составляют 400 тыс. р., ежедневные издержки хранения одного стекла — 6 тыс. р. Чему равен оптимальный размер заказа? Каковы минимальные годовые совокупные издержки?
Вариант 5
Годовой заказ на тостер «Слава» для салона Марии Мягковой равен 3000 единиц, или 10 вдень. Издержки заказа равны 25 тыс. р. издержки хранения — 0,4 тыс. р. в день. Так как тостер «Слава» является очень популярным среди покупателей, то в случае отсутствия товара покупатели обычно согласны подождать, пока не подойдет следующий заказ. Однако издержки, связанные с дефицитом, равны 0,75 тыс .р. за тостер в день. Сколько тостеров будет оказывать Мария? Каков максимальный дефицит? Чему равны совокупные издержки?
Вариант 6
Магазин «Природа» пользуется популярностью у покупателей благодаря широкому ассортименту экологически чистых продуктов. Большинство покупателей не отказываются от услуг магазина даже в том случае, когда интересующий их товар отсутствует в продаже. Они оставляют заказ на товар и ждут, когда поступит новая партия.
Сыр «Витаум» — не самый популярный из всего набора товаров, но администратор магазина регулярно заказывает этот продукт. Годовой спрос на «Витаум» составляет 500 головок сыра. Издержки заказа — 40 тыс. р. за заказ. Издержки хранения — 5 тыс. р. в год. Упущенная прибыль вследствие дефицита составляет 100 тыс. р. за год на одну головку сыра.
Сколько головок сыра следует заказывать, чтобы не допустить дефицита и иметь при этом минимальные общие издержки?
Сколько сыра следует заказывать, если допустить возможность дефицита?
Чему равна точка восстановления запаса, если время выполнения заказа 10 дней и число рабочих дней в году 250?
Чему равен максимальный размер дефицита?
Вариант 7
Компания «Химпласт» предлагает следующие скидки для линолеума размером 2х3 м (табл. 6.3).
Таблица 6.3
|
Размер заказа |
9 кусков или менее |
10-50 кусков |
50 кусков и более |
Цена 1 куска |
18 тыс. р. |
17,5 тыс. р. |
17,25 тыс. р. |
Магазин «Все для дома» заказывает у компании линолеум. Издержки заказа равны 45 тыс. р. Годовые издержки хранения равны 50% от цены. Годовой спрос на линолеум в магазине составляет 100 кусков. Какое количество необходимо приобрести?
Вариант 8
Мебельный салон «Антика» продает в год около 1000 спальных гарнитуров по цене 50 млн. р. Размещение одного заказа на поставку гарнитуров обходится в 40 млн. р. Годовая стоимость хранения гарнитура составляет 25% его цены. Салон может получить 3%-ю скидку у поставщика, если размер заказа составит не менее 200 гарнитуров. Следует ли салону заказывать 200 или более гарнитуров и пользоваться скидкой?
Вариант 9
Обычная оптовая цена аудиоколонок для автомагнитолы — 20 тыс. р. В случае заказа от 75 до 90 колонок цена сокращается до 18,5 тыс. р. При заказе более 100 колонок цена снижается до 15,75 тыс. р. Издержки заказа для компании «Эхо», являющейся производителем колонок, равны 10 тыс. р., годовые издержки хранения — 5% от стоимости колонки. Ежедневная величина спроса в течение 250 дней реализации в году — 25 колонок. Каков оптимальный размер заказа и чему равны минимальные средние ежедневные издержки?
Вариант 10
Компания «Интегро» продает в год около 2000 шкафов-купе по цене 40 тыс. р. Размещение одного заказа на поставку шкафов-купе обходится в 30 тыс. р. Годовая стоимость хранения гарнитура составляет 20% его цены. Компания может получить 5%-ю скидку у поставщика, если размер заказа составит не менее 300 гарнитуров. Следует ли салону заказывать 300 или более гарнитуров и пользоваться скидкой?
Вариант 11
Компания «Люкс» предлагает следующие скидки для обоев (табл.6.4).
Таблица 6.4
|
Размер заказа |
10 метров и менее |
10-100 метров |
Более 100 метров |
Цена 1 метра |
300 р. |
250 р. |
210 р. |
Магазин «Уют» заказывает у компании обои. Издержки заказа равны 50 тыс. р. Годовые издержки хранения равны 40% от цены. Годовой спрос на линолеум в магазине составляет 2000 метров. Какое количество необходимо приобрести?
Вариант 12
Петр Иванович из компании «Уют» продает 600 спален в год, причем издержки хранения равны 500 р. за кровать в день и издержки заказа — 50 тыс. р. Количество рабочих дней равно 250 и время выполнения заказа — 5 дней. Каков оптимальный размер заказа? Чему равна точка восстановления запаса? Каков оптимальный размер заказа, если издержки хранения равны 1 тыс. р.?
Вариант 13
Иванов Иван является владельцем компании, которая изготовляет игрушки. В среднем компания может производить 50 игрушек в день. Дневной спрос на игрушки примерно равен 40. Фиксированные издержки производства равны 100 тыс. р., издержки хранения — 20 тыс. р. за игрушку в год. Какой максимальный заказ следует иметь на складе?
Вариант 14
Иван Федорович приобретает в течение года 300 видеомагнитофонов для розничной продажи в своем магазине. Издержки хранения каждого магнитофона равны 20 тыс. р. в год. Издержки заказа — 100 тыс. р. Количество рабочих дней в году равно 300, время выполнения заказа — 5 дней. Необходимо найти:
-
оптимальный размер заказа;
-
годовые издержки заказа;
-
точку восстановления запаса.
Вариант 15
Фирма приобретает в течение года 1000 компьютеров для розничной продажи. Издержки хранения каждого компьютера равны 25 тыс. р. в год. Издержки заказа — 300 тыс. р. Количество рабочих дней в году равно 290, время выполнения заказа — 10 дней. Необходимо найти:
-
оптимальный размер заказа;
-
годовые издержки заказа;
-
точку восстановления запаса.
Контрольные вопросы
1. Что такое время выполнения заказа?
2. Что такое время цикла?
3. Что такое запас?
4. Что такое издержки заказа?
5. Что такое издержки хранения?
6. Что такое точка восстановления?
7. Что такое упущенная прибыль?
8. Какие модели управления запасами Вы знаете?
9. Опишите модель оптимального размера заказа.
10. Опишите модель заказа с количественными ссылками.
З повагою ІЦ «KURSOVIKS»!
Задача 1. Мистер Бобров приобретает в течение года 1500 телевизоров для розничной продажи в своем магазине. Издержки хранения каждого телевизора равны 45 руб. в год. Издержки заказа — 150 руб. Количество рабочих дней в году равно 300, время выполнения заказа — 6 дней.
Вопросы:
1. Каков оптимальный размер заказа?
2. Чему равны годовые издержки заказа?
3. Чему равна точка восстановления запаса?
Задача 2. Анна Васильева из компании «Сюрприз» продает 400 водяных кроватей в год, причем издержки хранения равны 1 тыс. руб. за кровать в день, а издержки заказа — 40 тыс. руб. Количество рабочих дней равно 250, время выполнения заказа — 6 дней.
Вопросы:
1. Каков оптимальный размер заказа?
2. Чему равна точка восстановления запаса?
3. Каков оптимальный размер заказа, если издержки хранения равны 1,5 тыс. руб.?
Задача 3. Мекки Мессер владеет маленькой компанией, которая выпускает электрические ножи. В среднем она может производить 150 ножей в день. Дневной спрос на ножи примерно равен 40 шт. Фиксированные издержки производства составляют 100 руб., издержки хранения — 8 руб. за нож в год. В году 250 рабочих дней.
Вопросы:
1. Каков оптимальный размер производственного заказа?
2. Чему равны издержки хранения?
3. Чему равны совокупные издержки за год?
Задача 4. Годовой заказ на тостер «Слава» для магазина Марии Монеты — 3000 единиц, или 10 единиц в день. Издержки заказа равны 25 руб., издержки хранения — 0,4 руб. в день. Так как тостер «Слава» очень популярен, то в случае отсутствия товара покупатели обычно согласны подождать, пока не поступит следующая партия товара. Однако издержки вследствие дефицита равны 0,75 руб. за тостер в день.
Вопросы:
1. Сколько тостеров будет заказывать Мария?
2. Каков максимальный дефицит?
3. Чему равны совокупные издержки?
Задача 5. Магазин «Все для дома» закупает линолеум размером 2 х 3 м2 в компании «Химические товары». В зависимости от размера заказа компания предлагает следующие скидки:
Издержки заказа равны 45 тыс. руб. Годовые издержки хранения составляют 50% от закупочной цены, годовой спрос на линолеум равен 100 кускам. Определите оптимальный размер заказа.
Задача 6. Мебельный салон «Антик» продает в год около 1000 спальных гарнитуров по цене 50 тыс. руб. Размещение одного заказа на поставку гарнитуров обходится в 40 тыс. руб. Годовая стоимость хранения гарнитура составляет 25% его цены. Салон может получить у поставщика скидку в 3%, если размер заказа составит не менее 200 гарнитуров. Следует ли салону воспользоваться этой скидкой?
| < Предыдущая | Следующая > |
|---|


Подборка по базе: Практическая работа № 3.docx, Практическая работа.docx, (1-5 заданий) — Контрольная работа №6 — Ряды.pdf, (1-5 заданий) — Контрольная работа №8 -ТФКП.pdf, Практическая работа №1.docx, Контрольная работа 8 класс.docx, Ситуационные задачи с решением по уголовному процессуальному пра, Практическая работа № 1.docx, (1-5 заданий)-Контрольная работа №3-Неопределенные интегралы.pdf, Лабораторная работа 1_2022.docx
Выберем тот размер заказа, который минимизирует общие годовые издержки. Из таблицы видно, что заказ в размере 1000 игрушечных гоночных машинок будет минимизировать совокупные издержки.
Индивидуальное задание
Решить задачу, согласно вашему варианту, используя модели управления запасами.
Вариант 1
Господин Бобров приобретает в течение года 1500 телевизоров для розничной продажи в своем магазине. Издержки хранения каждого телевизора равны 45 тыс. р. в год. Издержки заказа — 150 тыс. р. Количество рабочих дней в году равно 300, время выполнения заказа — 6 дней. Необходимо найти:
- оптимальный размер заказа;
- годовые издержки заказа;
- точку восстановления запаса.
Вариант 2
Анна Васильева из компании «Сюрприз» продает 400 водяных кроватей в год, причем издержки хранения равны 1 тыс. р. за кровать в день и издержки заказа — 40 тыс. р. Количество рабочих дней равно 250 и время выполнения заказа — 6 дней. Каков оптимальный размер заказа? Чему равна точка восстановления запаса? Каков оптимальный размер заказа, если издержки хранения равны 1,5 тыс. р.?
Вариант 3
Мекки Мессер является владельцем маленькой компании, которая выпускает электрические ножи. В среднем Мекки может производить 150 ножей в день. Дневной спрос на ножи примерно равен 40. Фиксированные издержки производства равны 100 тыс. р., издержки хранения — 8 тыс. р. за нож в год. Какой максимальный заказ следует иметь на складе?
Вариант 4
Компания «Веселые ребята» закупает у завода-изготовителя лобовые стекла грузовых автомобилей «Урал» для розничной продажи. В год, за 200 рабочих дней, реализуется около 10 000 стекол. Издержки заказа для компании составляют 400 тыс. р., ежедневные издержки хранения одного стекла — 6 тыс. р. Чему равен оптимальный размер заказа? Каковы минимальные годовые совокупные издержки?
Вариант 5
Годовой заказ на тостер «Слава» для салона Марии Мягковой равен 3000 единиц, или 10 вдень. Издержки заказа равны 25 тыс. р. издержки хранения — 0,4 тыс. р. в день. Так как тостер «Слава» является очень популярным среди покупателей, то в случае отсутствия товара покупатели обычно согласны подождать, пока не подойдет следующий заказ. Однако издержки, связанные с дефицитом, равны 0,75 тыс .р. за тостер в день. Сколько тостеров будет оказывать Мария? Каков максимальный дефицит? Чему равны совокупные издержки?
Вариант 6
Магазин «Природа» пользуется популярностью у покупателей благодаря широкому ассортименту экологически чистых продуктов. Большинство покупателей не отказываются от услуг магазина даже в том случае, когда интересующий их товар отсутствует в продаже. Они оставляют заказ на товар и ждут, когда поступит новая партия.
Сыр «Витаум» — не самый популярный из всего набора товаров, но администратор магазина регулярно заказывает этот продукт. Годовой спрос на «Витаум» составляет 500 головок сыра. Издержки заказа — 40 тыс. р. за заказ. Издержки хранения — 5 тыс. р. в год. Упущенная прибыль вследствие дефицита составляет 100 тыс. р. за год на одну головку сыра.
Сколько головок сыра следует заказывать, чтобы не допустить дефицита и иметь при этом минимальные общие издержки?
Сколько сыра следует заказывать, если допустить возможность дефицита?
Чему равна точка восстановления запаса, если время выполнения заказа 10 дней и число рабочих дней в году 250?
Чему равен максимальный размер дефицита?
Вариант 7
Компания «Химпласт» предлагает следующие скидки для линолеума размером 2х3 м (табл. 6.3).
Таблица 6.3
| Размер заказа | 9 кусков или менее | 10-50 кусков | 50 кусков и более |
Цена 1 куска |
18 тыс. р. | 17,5 тыс. р. | 17,25 тыс. р. |
Лаврушина Е.Г., Слугина Н.Л. Теория систем и системный анализ — файл n1.doc
приобрести
Лаврушина Е.Г., Слугина Н.Л. Теория систем и системный анализ
скачать (3005 kb.)
Доступные файлы (1):
n1.doc
Рассмотрим пример, объясняющий принцип принятия решения в условиях скидки. Магазин «Медвежонок» продает игрушечные гоночные машинки. Эта фирма имеет таблицу скидок на машинки в случае покупок их в определенном количестве (табл. 6.1). Издержки заказа составляют 49 тыс. р. Годовой спрос на машинки равен 5000. Годовые издержки хранения в отношении к цене составляют 20%, или 0,2. Необходимо найти размер заказа, минимизирующий общие издержки.
Решение
Рассчитаем оптимальный размер заказа для каждого вида скидок, т.е. Q1*, Q2* и Q3*. и получим Q1* = 700; Q2* = 714; Q3* = 718.
Так как Q1* — величина между 0 и 999, то ее можно оставить прежней. Q2* меньше количества, необходимого для получения скидки, следовательно, его значение необходимо принять равным 1000 единиц. Аналогично Q3* берем равным 2000 единиц. Получим Q1* = 700; Q2* = 1000; Q3* = 2000.
Далее необходимо рассчитать общие издержки для каждого размера заказа и вида скидок, а затем выбрать наименьшее значение.
Рассмотрим следующую таблицу:
Таблица 6.2
| Вид скидки | 1 | 1 | 3 |
| Цена | 5 | 4,8 | 4,75 |
| Размер заказа | 700 | 1000 | 2000 |
| Цена на товар за год | 25000 | 24000 | 23750 |
| Годовые издержки заказа | 350 | 245 | 122,5 |
Годовые издержки хранения |
350 |
480 |
950 |
| Общие годовые издержки | 25700 | 24725 | 24822,5 |
Выберем тот размер заказа, который минимизирует общие годовые издержки. Из таблицы видно, что заказ в размере 1000 игрушечных гоночных машинок будет минимизировать совокупные издержки.
Индивидуальное задание
Решить задачу, согласно вашему варианту, используя модели управления запасами.
Вариант 1
Господин Бобров приобретает в течение года 1500 телевизоров для розничной продажи в своем магазине. Издержки хранения каждого телевизора равны 45 тыс. р. в год. Издержки заказа — 150 тыс. р. Количество рабочих дней в году равно 300, время выполнения заказа — 6 дней. Необходимо найти:
- оптимальный размер заказа;
- годовые издержки заказа;
- точку восстановления запаса.
Вариант 2
Анна Васильева из компании «Сюрприз» продает 400 водяных кроватей в год, причем издержки хранения равны 1 тыс. р. за кровать в день и издержки заказа — 40 тыс. р. Количество рабочих дней равно 250 и время выполнения заказа — 6 дней. Каков оптимальный размер заказа? Чему равна точка восстановления запаса? Каков оптимальный размер заказа, если издержки хранения равны 1,5 тыс. р.?
Вариант 3
Мекки Мессер является владельцем маленькой компании, которая выпускает электрические ножи. В среднем Мекки может производить 150 ножей в день. Дневной спрос на ножи примерно равен 40. Фиксированные издержки производства равны 100 тыс. р., издержки хранения — 8 тыс. р. за нож в год. Какой максимальный заказ следует иметь на складе?
Вариант 4
Компания «Веселые ребята» закупает у завода-изготовителя лобовые стекла грузовых автомобилей «Урал» для розничной продажи. В год, за 200 рабочих дней, реализуется около 10 000 стекол. Издержки заказа для компании составляют 400 тыс. р., ежедневные издержки хранения одного стекла — 6 тыс. р. Чему равен оптимальный размер заказа? Каковы минимальные годовые совокупные издержки?
Вариант 5
Годовой заказ на тостер «Слава» для салона Марии Мягковой равен 3000 единиц, или 10 вдень. Издержки заказа равны 25 тыс. р. издержки хранения — 0,4 тыс. р. в день. Так как тостер «Слава» является очень популярным среди покупателей, то в случае отсутствия товара покупатели обычно согласны подождать, пока не подойдет следующий заказ. Однако издержки, связанные с дефицитом, равны 0,75 тыс .р. за тостер в день. Сколько тостеров будет оказывать Мария? Каков максимальный дефицит? Чему равны совокупные издержки?
Вариант 6
Магазин «Природа» пользуется популярностью у покупателей благодаря широкому ассортименту экологически чистых продуктов. Большинство покупателей не отказываются от услуг магазина даже в том случае, когда интересующий их товар отсутствует в продаже. Они оставляют заказ на товар и ждут, когда поступит новая партия.
Сыр «Витаум» — не самый популярный из всего набора товаров, но администратор магазина регулярно заказывает этот продукт. Годовой спрос на «Витаум» составляет 500 головок сыра. Издержки заказа — 40 тыс. р. за заказ. Издержки хранения — 5 тыс. р. в год. Упущенная прибыль вследствие дефицита составляет 100 тыс. р. за год на одну головку сыра.
Сколько головок сыра следует заказывать, чтобы не допустить дефицита и иметь при этом минимальные общие издержки?
Сколько сыра следует заказывать, если допустить возможность дефицита?
Чему равна точка восстановления запаса, если время выполнения заказа 10 дней и число рабочих дней в году 250?
Чему равен максимальный размер дефицита?
Вариант 7
Компания «Химпласт» предлагает следующие скидки для линолеума размером 2х3 м (табл. 6.3).
Таблица 6.3
| Размер заказа | 9 кусков или менее | 10-50 кусков | 50 кусков и более |
Цена 1 куска |
18 тыс. р. | 17,5 тыс. р. | 17,25 тыс. р. |
Контрольный пример 2