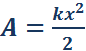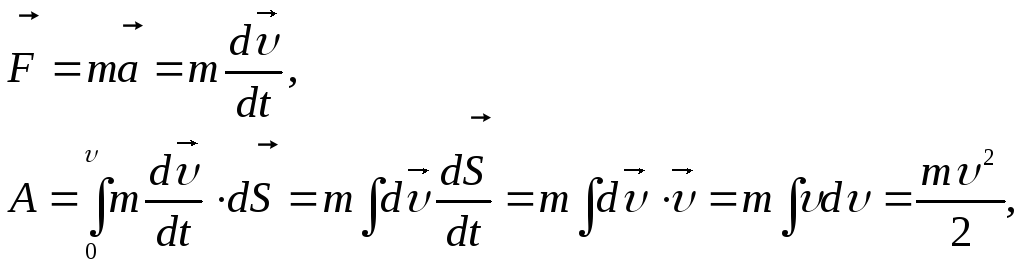Механическая работа совершаемая механизмом за конечный промежуток времени характеризует его мощность

Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы.

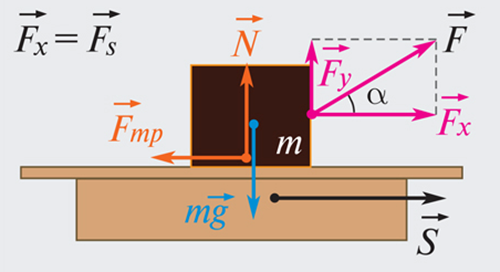
Если действующая на тело сила  вызывает его перемещение s, то действие этой силы характеризуется величиной, называемой механической работой (или, сокращенно, просто работой).

Механическая работа А — скалярная величина, равная произведению модуля силы F, действующей на тело, и модуля перемещения s, совершаемого телом в направлении действия этой силы.

Если направления перемещения тела и приложенный силы не совпадают, то работу можно вычислить как произведение модулей силы и перемещения, умноженному на косинус угла α между векторами силы   и перемещения  (рис. 1.18.1):

Работа является скалярной величиной. Она может быть как положительной (0° ≤ α < 90°), так и отрицательной (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж).

Джоуль равен работе, совершаемой силой в 1 Н на перемещении 1 м в направлении действия силы.

Рисунок 1.18.1. Работа силы :

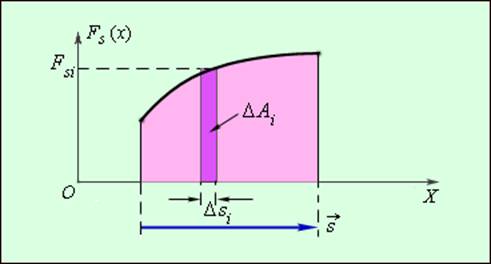
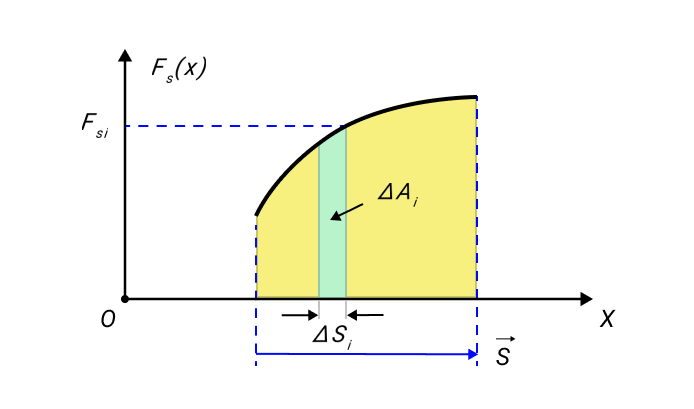
Если проекция  силы  на направление перемещения  не остается постоянной, работу следует вычислять для малых перемещений Δsi и суммировать результаты:

Это сумма в пределе (Δsi → 0) переходит в интеграл.

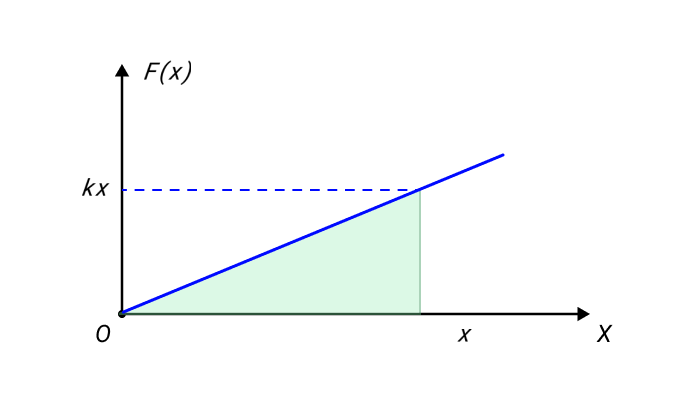
Графически работа определяется по площади криволинейной фигуры под графиком Fs(x) (рис. 1.18.2).

Рисунок 1.18.2. Графическое определение работы. ΔAi = FsiΔsi

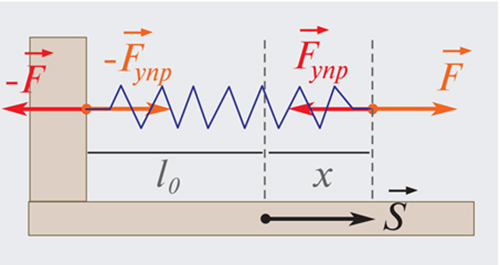
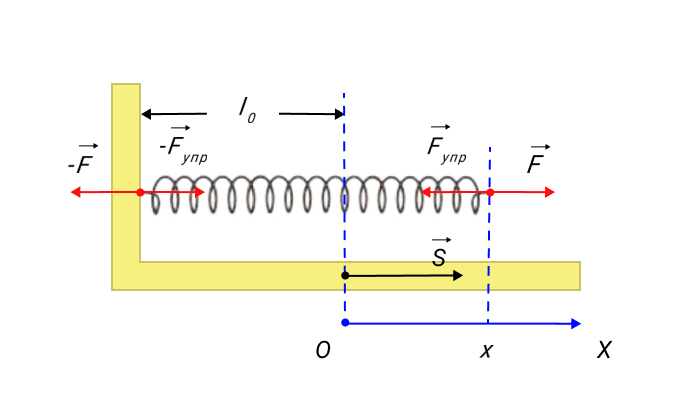
Примером силы, модуль которой зависит от координаты, может служить сила упругости пружины, подчиняющаяся закону Гука. Для того, чтобы растянуть пружину, к ней нужно приложить внешнюю силу  модуль которой пропорционален удлинению пружины (рис. 1.18.3).

Рисунок 1.18.3. Растянутая пружина. Направление внешней силы  совпадает с направлением перемещения  :    k – жесткость пружины.

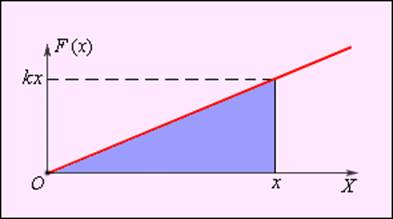
Зависимость модуля внешней силы от координаты x изображается на графике прямой линией (рис. 1.18.4).

Рисунок 1.18.4. Зависимость модуля внешней силы от координаты при растяжении пружины

По площади треугольника на рис. 1.18.4 можно определить работу, совершенную внешней силой, приложенной к правому свободному концу пружины:

Этой же формулой выражается работа, совершенная внешней силой при сжатии пружины. В обоих случаях работа упругой силы  равна по модулю работе внешней силы  и противоположна ей по знаку.

Если к телу приложено несколько сил, то общая работа всех сил равна алгебраической сумме работ, совершаемых отдельными силами. При поступательном движении тела, когда точки приложения всех сил совершают одинаковое перемещение, общая работа всех сил равна работе равнодействующей приложенных сил.

Модель. Механическая работа.

Мощность

Работа силы, совершаемая в единицу времени, называется мощностью. Мощность N это физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа:

В Международной системе (СИ) единица мощности называется ватт (Вт). Ватт равен мощности силы, совершающей работу в 1 Дж за время 1 с.

Когда под действием
некоторой силы тело совершает перемещение,
то действие силы характеризуется
величиной, которая называется механической
работой.

Механическая
работа
— мера действия силы, в результате
которого тела совершают перемещение.

Работа
постоянной силы.
Если тело движется прямолинейно под
действием постоянной силы
,
составляющей некоторый угол 
с направлением перемещения

(рис.1), работа равна произведению этой
силы на перемещение точки приложения
силы и на косинус угла 
между векторами
и

;
или работа равна скалярному произведению
вектора силы на вектор перемещения:

.

1 Дж — работа,
совершаемая силой в 1Н при перемещении
на 1м в направлении действия силы.

1. если 
   — острый угол,
   ,;

2. если 
   — тупой угол,
   ,;

3. если
   ,.

Работа
переменной силы.
Чтобы найти работу переменной силы,
пройденный путь разбивают на большое
число малых участков так, чтобы их можно
было считать прямолинейными, а действующую
в любой точке данного участка силу —
постоянной.

Элементарная
работа (т.е. работа на элементарном
участке
)
равна
,
а вся работа переменной силы на всем
пути S
находится интегрированием:
.

Для характеристики
быстроты совершения работы вводят
понятие мощности.

Мощность
постоянной силы
численно равна работе, совершаемой этой
силой за единицу времени.

.

1 Вт- это мощность
силы, которая за 1 с совершает 1 Дж работы.

В случае переменной
мощности (за малые одинаковые промежутки
времени совершается различная работа)
вводится понятие мгновенной мощности:

,

где

скорость
точки приложения силы.

Т.о.
мощность равна скалярному произведению
силы
на
скорость

точки её приложения.

1. Кинетическая и
   потенциальная энергии. Законы сохранения
   энергии и импульса.

Все введенные
ранее величины характеризовали только
механическое движение. Однако форм
движения материи много, постоянно
происходит переход от одной формы
движения к другой. Необходимо ввести
физическую величину, характеризующую
движение материи во всех формах её
существования, с помощью которой можно
было бы количественно сравнивать
различные формы движения материи.

Энергия численно
равна максимальной работе, которую тело
может совершить, и измеряется в тех же
единицах, что и работа. При переходе
энергии из одного вида в другой нужно
подсчитать энергию тела или системы до
и после перехода и взять их разность.
Эту разность принято называть работой:

.

Т. о., физическая
величина, характеризующая способность
тела совершать работу, называется
энергией.

Механическая
энергия тела может быть обусловлена
либо движением тела с некоторой скоростью,
либо нахождением тела в потенциальном
поле сил.

Кинетическая
энергия.

Энергия,
которой обладает тело вследствие своего
движения, называется кинетической.

Работа, совершенная
над телом, равна приращению его
кинетической энергии.

Найдем
эту работу для случая, когда равнодействующая
всех приложенных к телу сил равна
.

,

Работа, совершенная
телом за счет кинетической энергии,
равна убыли этой энергии.

Потенциальная
энергия.

Если в каждой точке
пространства на тело воздействуют
другие тела с силой, величина которой
может быть различна в разных точках,
говорят, что тело находится в поле сил
или силовом поле.

Все силы в механике
подразделяются на консервативные и
неконсервативные (или диссипативные).

Силы,
работа которых не зависит от формы
траектории, а определяется только
начальным и конечным положением тела
в пространстве, называются консервативными.

Силы,
работа которых зависит от формы пути,
называются неконсервативными
(силы трения).

Потенциальной
энергией называют часть общей механической
энергии системы, которая определяется
только взаимным расположением тел,
составляющих систему, и характером сил
взаимодействия между ними. Потенциальная
энергия
— это энергия, которой обладают тела или
части тела вследствие их взаимного
расположения.

В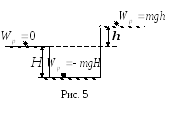каждой конкретной задаче уславливаются
считать потенциальную энергию какого-то
определенного положения тела равной
нулю, а энергию других положений брать
по отношению к нулевому уровню. Конкретный
вид функции

зависит от характера силового поля и
выбора нулевого уровня. Поскольку
нулевой уровень выбирается произвольно,

может иметь отрицательные значения.
Например, если принять за нуль потенциальную
энергию тела, находящегося на поверхности
Земли, то в поле сил тяжести вблизи
земной поверхности потенциальная
энергия тела массой m,
поднятого на высоту h
над поверхностью, равна

(рис. 5).

Потенциальная
энергия этого же тела, лежащего на дне
ямы глубиной H,
равна

.

В рассмотренном
примере речь шла о потенциальной энергии
системы Земля-тело.

Потенциальной
энергией может обладать не только
система взаимодействующих тел, но
отдельно взятое тело. В этом случае
потенциальная энергия зависит от
взаимного расположения частей тела.

—
потенциальная энергия упругой деформации,
если принять, что потенциальная энергия
недеформированного тела равна нулю;

где
k
— коэффициент упругости, x
— деформация тела.

В общем случае
тело одновременно может обладать и
кинетической и потенциальной энергиями.
Сумма этих энергий называется полной
механической энергией тела:

Полная механическая
энергия системы равна сумме её кинетической
и потенциальной энергий. Полная энергия
системы равна сумме всех видов энергии,
которыми обладает система.

Механической
системой называется совокупность тел,
выделенная для рассмотрения. Тела,
образующие механическую систему, могут
взаимодействовать, как между собой, так
и с телами, не принадлежащими данной
системе. В соответствие с этим силы,
действующие на тела системы, подразделяют
на внутренние и внешние.

Внутренними
называются силы, с которыми тела системы
взаимодействуют между собой

Внешними называются
силы, обусловленные воздействием тел,
не принадлежащих данной системе.

Замкнутой
(или изолированной) называется система
тел, на которую не действуют внешние
силы.

Для
замкнутых систем оказываются неизменными
(сохраняются) три физических величины:
энергия, импульс и момент импульса. В
соответствии с этим имеют место три
закона сохранения: энергии, импульса,
момента импульса.

Закон сохранения
энергии — результат обобщения многих
экспериментальных данных. Идея этого
закона принадлежит Ломоносову, изложившему
закон сохранения материи и движения, а
количественная формулировка дана
немецким врачом Майером и естествоиспытателем
Гельмгольцем.

Закон
сохранения механической энергии:
в поле только консервативных сил полная
механическая энергия остается постоянной
в изолированной системе тел. Наличие
диссипативных сил (сил трения) приводит
к диссипации (рассеянию) энергии, т.е.
превращению её в другие виды энергии и
нарушению закона сохранения механической
энергии.

Закон
сохранения и превращения полной энергии:
полная энергия изолированной системы
есть величина постоянная.

Сумма
импульсов тел, составляющих механическую
систему, называется импульсом системы:

Для системы тел
внутренние силы, согласно третьему
закону Ньютона, попарно равны и
противоположно направлены, т.е. их
геометрическая сумма равна нулю.

Т.о.,
производная по времени импульса
механической системы равна геометрической
сумме внешних сил, действующих на
систему,

Для
замкнутой системы
.

Закон
сохранения импульса:
импульс замкнутой системы материальных
точек остается постоянным.

Из этого закона
следует неизбежность отдачи при стрельбе
из любого орудия. Пуля или снаряд в
момент выстрела получают импульс,
направленный в одну сторону, а винтовка
или орудие получают импульс, направленный
противоположно. Для уменьшения этого
эффекта применяют специальные
противооткатные устройства, в которых
кинетическая энергия орудия превращается
в потенциальную энергию упругой
деформации и во внутреннюю энергию
противооткатного устройства.

Закон сохранения
импульса лежит в основе движения судов
(подводных лодок) при помощи гребных
колес и винтов, и водометных судовых
двигателей (насос всасывает забортную
воду и отбрасывает ее за корму). При этом
некоторое количество воды отбрасывается
назад, унося с собой определенный
импульс, а судно приобретает такой же
импульс, направленный вперед. Этот же
закон лежит в основе реактивного
движения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

В данной теме речь пойдёт о механической
работе и мощности.

Механическая работа — это скалярная физическая величина,
которая характеризует процесс перемещения тела под действием силы. Под
действием постоянной силы тело двигается прямолинейно и совершает перемещение в
направлении действия силы, то сила совершает работу, равную произведению модуля
этой силы и модуля перемещения.

Из определения следует единица
измерения работы в метрической системе единиц

Эта единица названа в честь
английского ученого Джеймса Прескотта Джоуля, впервые экспериментально
обосновавшего эквивалентность работы и теплоты.

Это самый простой случай,
когда перемещение тела и сила, действующая на него, совпадают по направлению.

Теперь рассмотрим, как
вычисляется работа, когда направление действия силы не совпадает с направлением
перемещения тела. Для этого рассмотрим следующий опыт. Через блок перекинута
нить на которой висит брусок некоторой массы. На брусок действуют две силы —
сила тяжести и сила натяжения нити.

Если равномерно тянуть за
нить, то тело будет равномерно двигаться, и, следовательно, результирующая
сила, действующая на тело, будет равна нулю.

Значит, при некотором
перемещении тела работа результирующей силы тоже будет равна нулю.

Однако сила натяжения нити совершает
работу.

Поскольку при равномерном
движении сила натяжения нити по модулю равна силе тяжести тела, то можно
предположить, что сила тяжести совершает такую же работу по величине, но
отрицательную.

Отсюда можно сделать вывод: работа
силы может быть положительной, отрицательной или равной нулю.

Заметим, что сила тяжести по
направлению противоположна перемещению тела. Это обстоятельство и другие
соображения позволяют предложить общую формулу для работы постоянной силы при
равномерном прямолинейном движении. Если вектор силы и перемещения составляют
между собой угол a, то работа этой силы равна
произведению модуля силы на модуль перемещения и на косинус угла между ними.

Это и есть общее выражение для
работы постоянной силы.

Из этой формулы видно, что в
случае, когда угол между направлением вектора силы и вектора перемещения
острый, то косинус этого угла будет больше нуля и, следовательно, больше
нуля будет работа силы.

Если вектор силы и вектор
перемещения составляют между собой тупой угол, то значение косинуса
этого угла меньше нуля. Значит и работа этой силы будет отрицательна.

И, наконец, если вектор
силы перпендикулярен вектору перемещения, то работа не
совершается (вернее, работа этой силы равна нулю).

Если к движущемуся телу
приложено несколько сил, то каждая из них совершает работу, а общая работа
равна алгебраической сумме работ, совершаемых отдельными силами.

Работу, совершенную силой, можно найти и графически.
Так, если действие силы на тело не меняется с течением времени и совпадает по
направлению с перемещением, то работа этой силы численно равна
площади заштрихованного прямоугольника.

Если же сила изменяется в
процессе движения, то работа этой силы тоже будет численно равна площади под
кривой. В частности, на рисунке представлен график силы, которая линейно
уменьшается с пройденным расстоянием до нуля. Очевидно, что работа этой силы
на пройденном пути, численно равна площади треугольника.

Ранее говорилось, что
основными силами в механике являются гравитационные силы (в частности сила
тяжести), силы упругости и силы трения.

Проанализируем более подробно работы,
совершаемые каждой из этих сил. Начнем с работы силы тяжести. Будем ее
рассматривать считая, что тело находится на небольших расстояниях от
поверхности Земли. В этом случае сила тяжести будет постоянной по модулю равной

Пусть тело массой m
падает с некоторой высоты h₁ до
высоты h₂. Тогда модуль
перемещения тела равен разности этих высот

Так как направления
перемещения и силы совпадают, то работа силы тяжести положительна и равна
произведению модуля силы тяжести и разности высот.

Следует помнить, что высоты,
на которых находится тело, можно отсчитывать от любого уровня. Это может быть
уровень поверхности Земли, пола или поверхности стола. Высоту выбранного уровня
принимают равной нулю. Поэтому этот уровень называют нулевым. Так, если тело
падает с высоты h до нулевого уровня, то работа силы тяжести равна

Теперь выясним, какую работу
совершает сила тяжести, если тело движется не по вертикали. Для этого
рассмотрим движение тела по наклонной плоскости.

Пусть тело некоторой массы m
совершило перемещение, равное по модулю длине наклонной плоскости. Работа силы
тяжести в этом случае равна

Из рисунка видно, что

Поэтому работа силы тяжести в
этом случае также равна

Таким образом, получили для
работы силы тяжести такое же выражение, как и в случае движения тела по
вертикали. Отсюда следует главный вывод о том, что работа силы тяжести не
зависит от того, по какой траектории движется тело и всегда равна произведению
модуля силы тяжести на разность высот в начальном и конечном положениях тела.

Тогда очевидно, что если
тело движется по замкнутой траектории, где начальное и конечное положения
тела совпадают, то работа силы тяжести равна нулю. Напомним, что такие
силы, работа которых не зависит от формы траектории, а определяется только
начальным и конечным положениями тела в пространстве, называются потенциальными
или консервативными. Следовательно, сила тяжести — это консервативная
сила.

Теперь проанализируем работу,
совершаемую силой упругости. Сила упругости — это сила, возникающая при
деформации тела внешними воздействиями.

Рассмотрим систему, состоящую
из пружины и тела некоторой массы, лежащего на достаточно гладкой
горизонтальной поверхности. Левый конец пружины прикреплен к стене, а правый —
к телу. Направим ось икс так, как показано на рисунке.

Если тело сместить на
некоторое расстояние от положения равновесия, то пружина будет действовать на
него с силой упругости, направленной вправо. Модуль проекции этой силы на ось Ox
будет определяться на основании закона Гука.

Теперь отпустим тело. Тогда
под действием силы упругости пружины тело будет смещаться вправо.

При этом сила упругости будет
совершать работу. Предположим, что тело переместилось так, что расстояние от
положения равновесия стало х₂. Очевидно, что тогда модуль
перемещения тела равен разности между начальной и конечной координатой тела.

Для нахождения работы,
совершенной пружиной по перемещению тела, необходимо учесть, что сила упругости
меняется, так как ее величина зависит от удлинения пружины. Воспользуемся
графиком зависимости модуля силы упругости от удлинения пружины.

Известно, что работа силы
численно равна площади под графиком силы. В рассматриваемом
случае это площадь трапеции, основаниями которой являются силы упругости
пружины в положении один и два, а высота — это перемещение тела.

Из полученной формулы следует,
что работа силы упругости пружины зависит только от координат начального и
конечного положений. Из рисунка видно, что х₁ и х₂
— это и удлинение пружины, и координаты ее конца в выбранной системе координат.
Следовательно, работа силы упругости не зависит от формы траектории. А если
траектория замкнута, то работа равна нулю. Таким образом, сила упругости
является потенциальной силой.

И проанализируем работу,
совершаемую силой трения. Рассмотрим тело, находящееся на некоторой поверхности
(например, брусок на поверхности стола).

Если толкнуть брусок, то он
придет в движение, однако, через некоторое время, остановится. В процессе
движения бруска на него действуют: сила тяжести, сила нормальной реакции опоры
и сила трения скольжения. Под действием этих трех сил и движется брусок.
Поскольку сила тяжести компенсируется силой нормальной реакции стола, то
равнодействующая сила равна действующей на брусок силе трения. А так как сила
трения направлена противоположна перемещению, то работа этой силы будет
отрицательной (так как косинус ста восьмидесяти градусов равен минус единице).

Из формулы следует, что работа
силы трения зависит от модуля перемещения тела. И даже если тело
вернется в исходную точку, то работа силы трения не будет равна нулю.
Такие силы, работа которых зависит от формы траектории движения тела и на
замкнутой траектории отличны от нуля, называются непотенциальными или диссипативными
(от латинского — рассеяние).

Однако не надо думать, что
работа сил трения всегда отрицательна. Ведь именно благодаря силе трения покоя
человек и различные машины движутся по Земле. Действительно, при ходьбе человек
действует на поверхность Земли с некоторой силой F₁ (кроме силы нормальной реакции), а по третьему закону
Ньютона Земля действует на ногу человека с силой трения покоя, равной по модулю
силе воздействия человека, но противоположно направленной. Благодаря этой силе
человек движется. Сила трения покоя направлена также, как и скорость человека,
и, следовательно, работа этой силы положительна.

Таки образом, были рассмотрены
работы основных трех сил, с которыми чаще всего мы сталкиваемся в механике.
Однако, одна и та же работа в разных случаях может быть выполнена за различные
промежутки времени, то есть она может совершаться неодинаково быстро. Очевидно,
что чем меньшее времени требуется для выполнения данной работы, тем эффективнее
работает машина, механизм и прочее.

Величина, характеризующая
быстроту совершения работы, и равная отношению работы, совершаемой силой, к
промежутку времени, в течение которого она совершается, называется мощностью.

Исходя из определения видим,
что единицей измерения мощности является

Эта единица получила название Ватт,
в честь английского ученого Джеймса Уатта — изобретателя универсального
парового двигателя.

При движении любого тела на
него в общем случае действует несколько сил, каждая из которых совершает работу
и, следовательно, для каждой силы можно вычислить мощность. Так, если тело
движется прямолинейно и на него действует постоянная сила, то она совершает
работу, равную

Тогда мощность силы равна
отношению работы этой силы к промежутку времени.

Мощность силы также равна
произведению модуля силы на модуль скорости и на косинус угла между
направлениями вектора силы и вектора скорости.

По записанной формуле можно
рассчитывать и среднюю, и мгновенную мощности, подставляя значение средней или
мгновенной скорости.

Из полученной формулы следует,
что при заданной мощности мотора сила тяги тем меньше, чем больше скорость
движения. Вот почему водители автомобилей при подъеме в гору, когда нужна
наибольшая сила тяги, переключают двигатель на пониженную передачу.

И так, любой двигатель
или механическое устройство предназначены для выполнения определенной механической работы.
Эта работа называется полезной работой. Для двигателя автомобиля
— это работа по его перемещению, для токарного станка — работа по вытачиванию
детали.

Однако в любой машине, в
любом двигателе полезная работа всегда меньше той энергии, которая
затрачивается для приведения их в действие, потому что всегда существуют
силы трения, работа которых приводит к нагреванию каких-либо частей устройства.
А нагревание нельзя считать полезным результатом действия машины. Поэтому
каждое устройство характеризуется особой величиной, которая показывает,
насколько эффективно используется подводимая к нему энергия. Эта величина
называется коэффициентом полезного действия и обычно обозначается
греческой буквой h.

И так, коэффициентом
полезного действия называется отношение полезной работы, совершенной
машиной за некоторый промежуток времени, ко всей затраченной работе (или
подведенной энергии) за тот же промежуток времени.

Коэффициент полезного действия
обычно выражается в процентах. Поскольку и полезную, и затраченную работы можно
представить, как произведение мощности на промежуток времени в течение которого
работала машина, то

Основные выводы:

Рассмотрели важную физическую величины
– работу. Рассмотрели работы наиболее
часто встречающихся сил — силы тяжести, упругости и силы трения. Повторили
понятие мощности, а также вспомнили, что называют коэффициентом полезного
действия механизма.

Механическая работа и
мощность.

Механическая работа – процесс изменения механического состояния
тела под действием внешних сил.

Механическая работа  – пространственная характеристика действия
силы.

Механическая
работа  – скалярная
физическая величина, равная произведению модуля силы, модуля перемещения и
косинуса угла между ними.

Си: [A] =>
1Н∙м=1Дж.

1 Дж  – работа
силы в 1Н, вызывающей перемещение 1м, если направление силы совпадает с
направлением перемещения.

Работа —  величина скалярная, но может быть как
положительной, так и отрицательной:  Знак зависит от знака
косинуса угла.

1)    Если .

2)    Если .

3)      Работа равна нулю если:

а) Тело не совершает перемещение: .
Желая передвинуть шкаф, мы с силой на него надавливаем, но если при этом в
движение шкаф не приходит, то механическая работа не совершается.

б) Тело движется без участия сил: . Если тело движется по инерции,
работа не совершается.

в) Сила направлена перпендикулярно
перемещению: .
Сила, перпендикулярная скорости материальной точки, работу не совершает и не
изменяет модуля скорости тела. Не совершает работы сила, под действием которой
тело движется по окружности. Например, сила всемирного тяготения, под действием
которой спутники движутся по круговым орбитам.

Работа одной и той же силы может быть как положительной, так
отрицательной и равной нулю. Это зависит от  конкретных условий.

 

 

Рассчитаем работу силы тяжести в различных
случаях

:

1)     
Свободное падение тела:

 

2)     
Тело, брошенное вертикально вверх:

3)     
Тело, движущееся по горизонтальной дороге:

Совершенная
работа зависит от выбора системы отсчета. Ведь тело, неподвижное в одной
системе отсчета, будет перемещаться в другой, движущейся относительно первой.
Расстояние между телами одинаково во всех системах отсчета, но перемещение не
одинаково. Например, если человек стоит в поезде и просто удерживает растянутую
пружину, то в системе отсчета, связанной с поездом, рука человека не совершает
никакой работы, так как свободный конец пружины не перемещается. Но с точки
зрения наблюдателя в системе отсчета, связанной с Землей, работа будет
произведена. При переходе от одной системы отсчета к другой работа даже может
изменить знак, так как направление перемещения зависит от выбора системы
отсчета.

 

Если на тело действуют несколько сил, то полная работа на
конечном участке траектории равна работе результирующей силы  или
алгебраической сумме работ всех сил.

Найдем работу
всех сил, действующих на тело, при его перемещении по горизонтальной дороге:

Формула работы   справедлива в том случае,
когда сила постоянна и перемещение происходит вдоль прямой линии.

Если сила переменная , (или траектория
криволинейная), то участок пути разбивают на очень маленькие участки ΔS, такие, что силу на каждом из них можно считать постоянной по модулю и
направлению (такие, что их можно считать прямыми линиями), то

 –
элементарная работа.

 – полная работа

Если движение происходит с постоянной скоростью, то
, следовательно:

Графическое
представление работы:

1)      Если F∙cosα = const: (не зависит от координат и не изменяется
при перемещении материальной точки)

Если график
зависимости F∙cosα от  лежит
выше оси,
то работа силы F положительная; если график расположен под осью,
то работа силы F отрицательная.

2)      Если F∙cosα ≠ const: (сила меняется от точки  к точке
траектории)

Разбиваем фигуру на малые прямоугольники:

Работа силы численно равна площади фигуры,
ограниченной графиком изменения силы, осью и
ординатами, соответствующими начальной и конечной точкам траектории.

Работа как скалярное произведение:

В математике произведение модулей двух векторов на косинус угла между
ними называют скалярное произведение векторов. Следовательно, работа равна
скалярному произведению вектора силы на вектор перемещения.

Скалярное произведение двух векторов  можно выразить через произведения проекций этих векторов. Покажем это для
движения на плоскости.

Пусть . Разложим вектор  на составляющие   и , параллельные осям Х и У: . Тогда работа равна:

Но  и
,
следовательно:

Пусть . Тогда работа определяется
выражением:

Но  и
,
следовательно:

 –
совпадает с полученным ранее выражением.

В трехмерном случае эта
формула имеет вид:

Работа может быть совершена как за больший
промежуток времени, так и за очень малый. Когда говорят о производительности
работы, то определяют работу в единицу времени

Мощность – физическая
величина, равная отношению работы к интервалу времени, за который эта работа
совершена.

 

Мощность
характеризует быстроту совершения работы (работа, совершенная в единицу
времени). Чем меньше время, в течение которого механизм произвел данную работу,
или чем больше работа, которую он произвел за данное время, тем больше
мощность, которую этот механизм развивает.

Си: [N]
=> 1 =1Вт.

1 Вт  –
мощность тела, совершающего работу в 1Дж за 1с.

Если движение
происходит с постоянной скоростью: .

Механическая работа, мощность и КПД механизма

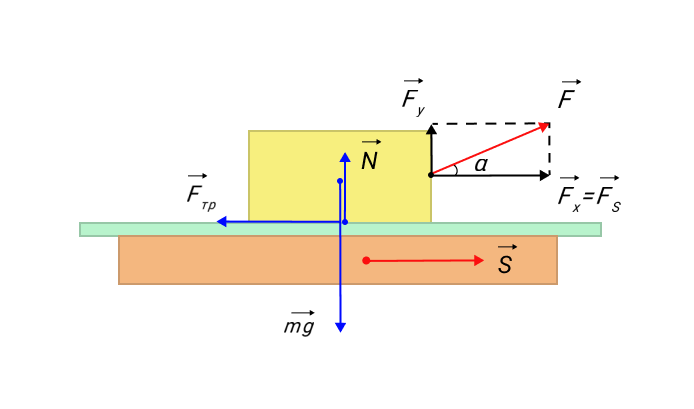
1. Механическая работа (или работа силы над телом) – физическая величина, равная по модулю произведению силы на путь, пройденный телом вдоль направления этой силы. Если вектор силы перпендикулярен направлению движения тела, то совершаемая этой силой работа равна нулю; если вектор силы сонаправлен с направлением движения тела, то работу силы считают положительной; если вектор силы противоположен направлению движения тела, то работу силы считают отрицательной.

• В случае, когда точка приложения силы перемещается в направлении действия силы, механическая работа А равна произведению модуля F силы на путь s, пройденный точкой приложения силы: А = Fs.
• Единица работы в СИ 1 Джоуль (Дж) = 1 Нм.
• «Золотое правило» механики с использованием понятия работы: никакой простой механизм не дает выигрыша в работе.

Таблица «Механическая работа, мощность и КПД»

---

2. Коэффициент полезного действия (КПД) – физическая величина, равная отношению полезной работы к полной совершённой работе. КПД показывает долю полезной работы от полной и, как и все доли, всегда имеет положительный знак и не имеет «своей» единицы для измерения. Значение КПД обычно выражают в процентах, которое нужно переводить в десятичную дробь для дальнейших вычислений.

• Коэффициентом полезного действия (КПД) механизма называют отношение полезной работы А_пол к совершенной А_сов, выраженное в процентах: η = А_пол/А_сов · 100%.
• КПД любого реального механизма меньше 100 % (из-за трения и из-за того, что сами механизмы и их части имеют некоторую массу).

3. Мощность действия – физическая величина, равная отношению механической работы ко времени, за которое она была совершена. Мощность характеризует быстроту (скорость) совершения работы. Мощность принято вычислять только для тех действий, в которых механическая работа положительна.

• Мощностью N называют отношение совершенной работы А к промежутку времени t, за который эта работа совершена: N = A/t
• Единица мощности в СИ 1 ватт (Вт) = 1 Дж/с.
• Мощность можно выразить через силу и скорость с помощью формулы N = Fv.

---

Схема «Механическая работа. Мощность»

---

Конспект урока по физике в 7 класса «Механическая работа и энергия».

Смотреть задачи: 1) на механическую работу,  2) механическую мощность, 3) на КПД простых механизмов.

Следующая тема: «Простые механизмы. Блоки»

Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы. Другими словами, работа — мера воздействия силы.

Определение механической работы

Работа А, совершаемая постоянной силой F→, — это физическая скалярная величина, равная произведению модулей силы и перемещения, умноженному на косинус угла α между векторами силы F→ и перемещением s→.

Данное определение рассматривается на рисунке 1.

Формула работы записывается как,

A=Fs cos α.

Работа – это скалярная величина. Единица измерения работы по системе СИ — Джоуль (Дж).

Джоуль равняется работе, совершаемой силой в 1 Н на перемещение 1 м по направлению действия силы.

Рисунок 1. Работа силы F→: A=Fs cos α=Fss

При проекции Fs→ силы F→ на направление перемещения s→ сила не остается постоянной, а вычисление работы для малых перемещений Δsi суммируется и производится по формуле:

A=∑∆Ai=∑Fsi∆si.

Данная сумма работы вычисляется из предела (Δsi→0), после чего переходит в интеграл.

Графическое изображение работы определяют из площади криволинейной фигуры, располагаемой под графиком Fs(x)рисунка 2.

Рисунок 2. Графическое определение работы ΔAi=FsiΔsi.

Примером силы, зависящей от координаты, считается сила упругости пружины, которая подчиняется закону Гука. Чтобы произвести растяжение пружины, необходимо приложить силу F→, модуль которой пропорционален удлинению пружины. Это видно на рисунке 3.

Рисунок 3. Растянутая пружина. Направление внешней силы F→ совпадает с направлением перемещения s→. Fs=kx, где k обозначает жесткость пружины.

F→упр=-F→

Зависимость модуля внешней силы от координат x можно изобразить на графике с помощью прямой линии.

Рисунок 4. Зависимость модуля внешней силы от координаты при растяжении пружины.

Из выше указанного рисунка возможно нахождение работы над внешней силой правого свободного конца пружины, задействовав площадь треугольника. Формула примет вид

A=kx22.

Данная формула применима для выражения работы, совершаемой внешней силой при сжатии пружины. Оба случая показывают, что сила упругости F→упр равняется работе внешней силы F→, но с противоположным знаком.

Если на тело действует несколько сил, то их общая работа равняется сумме всех работ, совершаемых над телом. Когда тело движется поступательно, точки приложения сил перемещаются одинаково, то есть общая работа всех сил будет равна работе равнодействующей приложенных сил.

Мощность

Мощностью называют работу силы, совершаемую в единицу времени.

Запись физической величины мощности, обозначаемой N, принимает вид отношения работы А к промежутку времени t совершаемой работы, то есть:

N=At.

Система СИ использует в качестве единицы мощности ватт (Вт). 1 Ватт — это мощность, которую совершает работу в 1 Дж за время 1 с.

Помимо Ватта, существуют и внесистемные единицы измерения мощности. Например, 1 лошадиная сила примерна равна 745 Ваттам.