Максимальное время выполнения всех предшествующих работ означает ранний срок наступления события

Определение критического пути

Будем
предполагать, что время выполнения
каждой работы точно известно. Введем
следующие определения.

Путь— последовательность взаимосвязанных
работ, ведущая из одной вершины проекта
в другую вершину. Например (см. Рисунок 48),
{A, D, G} и {C, F} – два различных пути.

Рисунок
48. Различные пути на сетевом графике

Длина
пути— суммарная продолжительность
выполнения всех работ пути.

Полный
путь— это путь от исходного к
завершающему событию.

Критический
путь— полный путь, суммарная
продолжительность выполнения всех
работ которого является наибольшей.

Очевидно,
что минимальное время, необходимое для
выполнения любого проекта равно длине
критического пути. Именно на работы,
принадлежащие критическому пути, следует
обращать особое внимание. Если такая
работа будет отложена на некоторое
время, то время окончания проекта будет
отложено на то же время. Если необходимо
сократить время выполнения проекта, то
в первую очередь нужно сократить время
выполнения хотя бы одной работы на
критическом пути.

Для
того, чтобы найти критический путь,
достаточно перебрать все пути и выбрать
тот, или те из них, которые имеют наибольшую
суммарную продолжительность выполнения
работ. Однако для больших проектов
реализация такого подхода связана с
вычислительными трудностями. Метод
критического пути (метод CPM — Critical Path
Method) позволяет получить критический
путь намного проще.

Расчет
сетевой модели начинают с временных
параметров событий, которые вписывают
непосредственно в вершины сетевого
графика (Рисунок 49):

• –ранний
  срок наступления события i, минимально
  необходимый для выполнения всех работ,
  которые предшествуют событию i;

• –поздний
  срок наступления события i, превышение
  которого вызовет аналогичную задержку
  наступления завершающего события сети;

• –резерв
  события i, т.е. время, на которое может
  быть отсрочено наступление события i
  без нарушения сроков завершения.

Рисунок
49. Параметры событий

Ранние
сроки наступления событий рассчитываются
от исходного (S) к завершающему (F) событию
следующим образом:

1. для
   исходного события S:
   ;

2. для
   всех остальных событий i:
   ,

где
максимум берется по всем работам (k,i),
входящим в событие i;
— длительность работы (k,i) (см. Рисунок 50).

Рисунок
50. Ранние сроки наступления событий

Поздние
сроки наступления событий
рассчитываются от завершающего к
исходному событию:

1. для
   завершающего события F:
   ;

2. для
   всех остальных событий i:
   ,

где
минимум берется по всем работам (i,j),
выходящим из события i;
— длительность работы (i,j) (см. Рисунок 51).

Рисунок
51. Поздние сроки наступления событий

Условия
критичности пути:

• необходимое
  условие: нулевые резервы событий,
  лежащих на критическом пути
  ;

• достаточное
  условие: нулевые полные резервы работ,
  лежащих на критическом пути
  .—
  показывает максимальное время, на
  которое можно увеличить длительность
  работы (i,j) или отсрочить ее начало,
  чтобы не нарушился срок завершения
  проекта в целом.

Пример

Рассмотрим
пример. Компания разрабатывает
строительный проект. Исходные данные
по основным операциям проекта представлены
в таблице. Нужно построить сетевую
модель проекта, определить критические
пути и проанализировать, как влияет на
ход выполнения проекта задержка работы
D на 4 недели.

Работа	Непосредственно предшествующая работа	Длительность, недели
A	—	4
B	—	6
C	A, B	7
D	B	3
E	C	4
F	D	5
G	E,F	3

Сетевой
график проекта показан на рисунке ниже
(см. Рисунок 52).

Рисунок
52. Пример. Сетевой график проекта

Согласно
необходимому условию два полных пути
сетевой модели (см. Рисунок 52)
имогут быть критическими. Проверим
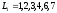
достаточное условие критичности для
работ (1,2) и (1,3)

,

.

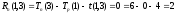
Путь
,
начинающийся с работы (1,3) не является
критическим, т.к. поскольку как минимум
одна из его работ не является критической.
Работа (1,3) имеет ненулевой полный резерв,
а значит может быть задержана с
выполнением, что недопустимо для
критических работ.

Таким
образом, сетевая модель имеет единственный
критический путь
длительностью 20 недель. За выполнением
работ этого пути необходим особый
контроль, т.к. любое увеличение их
длительности нарушит срок выполнения
проекта в целом.

Работа
D или (2,5) не является критической, ее
полный резерв равен 3-м неделям. Это
означает, что при задержке работы в
пределах 3-х недель срок выполнения
проекта не будет нарушен. Поэтому если
согласно условию работа D задержится
на 4 недели, то весь проект закончится
на 1 неделю позже.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #

Проводится также графическое упорядочение сети, чтобы уменьшить количество взаимно пересекающихся работ и зависимостей и расположить работы во временной последовательности.

Уровень детализации сетевых графиков зависит от сложности строящихся объектов, группировки и количества используемых ресурсов, объемов работ и периода строительства.

2.1. Расчет сетевой модели методом секторов

Существует несколько методов расчёта сетевых моделей. Известны методы расчёта сетевых графиков, в том числе метод «секторов», метод «потенциалов» и другие, кроме того, существуют табличные методы расчёта сетевых моделей. Наиболее распространённым является метод «секторов», при расчете которым события разделяются на четыре сектора (рис.).

Рис. Изображение события при расчёте сетевой

модели методом «секторов»

Порядок метода расчета сетевого графика. Рассмотрим пример (рис. ).

Рис. Сетевой график производства работ

Перед расчётом необходимо пронумеровать (кодировать) события. При этом должны выполняться правила:

• код-шифр события должен быть оригинальным, т.е. не должно быть событий с одинаковыми кодами;

• номера событий должны увеличиваться справа налево, т. е. от исходного события к завершающему (это скорее рекомендация).

Для больших моделей, содержащих сотни и тысячи работ, применяются специальные методы кодировки. Для простых графиков достаточно следовать правилам:

• первым нумеруется исходное событие;

• следующие номера присваивают событиям, непосредственно следующим за исходным;

• нумеруются события, у которых все предшествующие события пронумерованы, если таких событий несколько, то они нумеруются в произвольном порядке сверху вниз, а затем слева направо.

График с пронумерованными событиями показан на рис. 25.

Расчёт сетевого графика состоит из нескольких этапов:

• вычисление ранних сроков наступлений (свершений) событий – прямой ход;

• вычисление поздних сроков наступлений (свершений) событий – обратный ход;

• вычисление резервов времени событий;

• вычисление критического времени и определение критического пути;

• вычисление резервов времени работ.

Рис. График с пронумерованными событиями

При вычислении ранних сроков наступления событий (прямой ход) определяют ранний срок наступления событий. Ранний срок наступления события (Т^р_j) – это минимальный из возможных моментов наступления этого события при заданных продолжительностях работ и начальном моменте без учёта директивного срока завершения комплекса. Ранние сроки наступления событий определяются последовательно от исходного события к завершающему (рис.).

Моментом наступления исходного события (Т^р_о) или ранним сроком наступления его называется минимальный из моментов начала непосредственно следующих за ним работ:

,

где — раннее начало работы, непосредственно следующей за исходным событием.

Раннее начало любой работы равно раннему сроку наступления начального события этой работы:

.

Раннее окончание любой работы определяется как сумма раннего начала и продолжительности работы:

.

Моментом наступления промежуточного и завершающего события называется максимальный момент окончания непосредственно предшествующих ему работ.

Таким образом, ранний срок наступления промежуточных и завершающих событий определяется выражением:

;

,

где B(j) — множество событий i, соединённых с событиями j работами (ij).

Рис. Вычисление ранних сроков наступления событий

При вычислении поздних сроков наступления событий (обратный ход) определяют поздние сроки окончания событий. Поздний срок наступления события T^п_i – максимальный из допустимых моментов наступления данного события, при котором ещё возможно выполнения всех следующих работ с соблюдением директивного (или раннего, если директивный срок не задан) срока наступления события.

Поздний срок свершения завершающего события или вычисляется (при прямом ходе), или задаётся директивно (директивный срок – T_д). T^п_з=T^р_з, если директивный срок выполнения комплекса не задан. T^п_з=T_д, если директивный срок выполнения комплекса задан.

Вычислить поздний срок наступления данного события можно по формуле

;

,

где C(i) — множество событий j, соединённых с i работами (ij).

Выражение в скобках в формуле (3.5) представляет собой поздние начала работ, выходящих из события i, таким образом поздний срок наступления события i равен наименьшему из поздний начал выходящих из него работ.

Заметим, что позднее окончание работ, входящих в событие j, равно позднему сроку свершения этого события:

.

Рассмотрим все работы, входящие в событие j, и произведем вычисления (рис.).

Рис.. Вычисление поздних сроков наступления событий

Резервом времени события (R_i) называется промежуток времени, в течение которого событие наступит при заданных продолжительностях работ, начальном и конечном моментах (T ^р ₀ и T^п_з):

.

Резервы времени событий определяются в произвольном порядке (рис.).

Вычисление критического времени, определяется на основании выявления критического пути. Критическое время Т_к – минимальное время, в течение которого может быть выполнен весь комплекс работ.

Рис. Вычисление резервов времени событий

Критическое время определяется продолжительностью критического пути L_к:

,

которое определяется формулой

.

Критический путь – путь, имеющий максимальную продолжительность. Работы, лежащие на критическом пути — критические работы. Для определения критического пути необходимо определить критические работы.

Первый признак критической работы – начальное и конечное события этой работы — события с минимальными резервами времени. Исходное и завершающее события всегда лежат на критическом пути, а следовательно, всегда имеют минимальный резерв времени

,

или

.

Второй признак критической работы – критические работы имеют минимальный полный резерв времени выполнения работы.

Существуют три резерва времени работы: полный, свободный и частный. Полным резервом времени работы называется максимальное время, на которое можно отсрочить начало или увеличить продолжительность работы, не изменяя директивного (или раннего, если директивный не задан) срока наступления завершающего события (рис.).

Рис.. К выводу формулы полного резерва времени

Свободный резерв времени работы – максимальное время, на которое можно отсрочить начало или увеличить продолжительность работы при условии, что все события сети наступают в свои ранние сроки (рис.).

Рис.. К выводу формулы свободного резерва времени

Как следует из рис., полный резерв работы определяется выражением

.

Как следует из рис., свободный резерв работы определяется выражением

,

или

.

Частный резерв времени – максимальное время, на которое можно отсрочить начало или увеличить продолжительность работы при условии, что все события сети наступают в свои поздние сроки (рис. 31).

Рис. К выводу формулы частного резерва времени

Как следует из рис. 31, частный резерв работы определяется выражением

,

или

.

Задача 1.3. Плановый отдел компании собрал полную информацию о видах и параметрах основных годовых работ и составил сетевой план работ, представленный на рис. Известна технологическая последовательность работ, а также их продолжительность (Т_n), минимальное количество технически необходимых рабочих и фактически имеющееся количество исполнителей по каждой работе (N_n).

Определите параметры сетевого графика: ранний срок свершения события (T_i^p), поздний срок свершения события (T_i^п), резерв времени события (R_i), полный резерв времени работы (R^п), свободный резерв времени работы (R^св), частный резерв времени работы (R^ч).

Рис. . Сетевой график компании «Лего»

Решение 1.3. Представленный сетевой график относится к графикам, ориентированным на работы типа «работа-дуга».

Результаты расчета представлены на рис. Критический путь указан жирными стрелками.

Рис. . Расчет годового сетевого графика компании

2.2. Оптимизация сетевого графика работ по времени

Целью оптимизации сетевого графика является получение допустимого плана по ряду характеристик. План называется допустимым, если для каждой работы (ij) T _ij(н) и T _ij (о) удовлетворяют всем ограничениям, накладываемым исходной информацией модели.

Эти ограничения могут быть выражены в форме следующей системы неравенств:

• для всех пар работ, таких, что (ij) предшествует (k, l), T _k (н) ≥ T _ij(о); (ограничения на план, накладываемые сетью);

• для всех работ (ij) T_ij(н)≥T₀; T _ij(o) > T _ij(н) + T _ij (ограничения на план, накладываемые данными о продолжительности работ);

• если задан директивный срок, то T _ij(о)  Т_д (ограничения, накладываемые данными о начальном моменте и директивном сроке).

Методы оптимизации сетевого графика делятся на методы с привлечением дополнительных ресурсов и методы без привлечения дополнительных ресурсов, при этом возможно изменение сети или принятие исходного варианта.

Задача 1.4. Постройте оптимальный сетевой график производства, выполнив его оптимизацию по времени:

а) без привлечения дополнительных ресурсов:

• методом перераспределения ресурсов;

• методом деления работ на захватки;

б) с привлечением дополнительных ресурсов.

Исходный сетевой график представлен на рис..

Ранний срок — свершение — событие

Cтраница 1

Ранний срок свершения события tf характеризует наиболее ранний из возможных сроков наступления того или иного события. Срок его свершения определяется величиной наиболее длительного отрезка пути от исходного события до рассматриваемого.
 [1]

Ранний срок свершения события — это наиболее раннее время свершения данного события относительно начала выполнения комплекса работ. Отметим, что в реальной крупной сети число путей от ее начала до любого события, расположенного ближе к концу, может быть и очень велико. Поэтому прямо использовать приведенное выше определение для расчета ранних сроков событий не представляется возможным. Для этого используется специальный алгоритм, называемый алгоритмом Форда, существенно сокращающий объем проводимых вычислений: 1) для начального события сети всегда tpl 0; 2) для каждого последующего события по порядку выбирается максимум по всем его предкам tpj — max tpi у. L) в столбце таблицы равно числу предков у данного события; максимальное значение как-либо выделяется и используется для расчетов ранних сроков последующих событий.
 [2]

Если расчет ранних сроков свершения события ведется слева направо от начального события к конечному, то при определении поздних сроков свершения событий расчет нужно вести справа налево, от конечного события к начальному.
 [3]

Если расчет ранних сроков свершения события ведется слева направо, от начального события к конечному, то при определении поздних сроков свершения событий расчет нужно вести справа налево, от конечного события к начальному.
 [5]

Этот математический аппарат является попыткой уточнения оценки математического ожидания самых ранних сроков свершения событий, входящих в сетевую модель, с помощью аналитических методов. Метод, разработанный Фулкерсоном для случая дискретных распределений, был в дальнейшем обобщен Клингеном для случая непрерывных исходных функций распределения с получением соответствующего вычислительного алгоритма. Упомянутые методы расчета параметров сетевой модели со случайными оценками работы могут быть применены лишь для оценки средних значений самых ранних сроков свершения событий. Для получения же информации о законе распределения ранних сроков, в частности для получения информации о законе распределения самого раннего срока свершения завершающего события сети, т.е. времени выполнения сетевого проекта в целом, С. Я. Виленкиным предложен аналитический метод решения.
 [6]

В качестве / р ( а) всегда принимают максимальную величину, поскольку ранний срок свершения события равен максимальному пути, предшествующему данному событию. Аналогичным путем определяют этот показатель для всех других событий сети.
 [7]

На графике удобно определяется свободный резерв времени работ, который получают вычитанием из раннего срока свершения конечного события раннего срока свершения начального события ( цифры в левых секторах событий г и) и продолжительности самой работы.
 [9]

Начиная от начального события в сети, по каждому последующему событию ранний срок наступления его устанавливают как сумму раннего срока свершения предыдущего события и продолжительности связывающей их работы. Полученные числа записываем в левый сектор соответствующего события.
 [10]

На рис. 4.8 показано определение ранних сроков свершения событий. Ранний срок свершения исходного события принимается равным нулю. Ранний срок свершения / — го события определяется прибавлением продолжительности работы, ведущей к / — му событию, к раннему сроку предшествующего ему 1-го события. Если / — му событию предшествует несколько работ, то находятся величины ранних сроков выполнения каждой из этих работ и из них выбирается максимальная.
 [12]

В качестве tp ( i) всегда принимают максимальное значение, поскольку ранний срок свершения события равен максимальному пути, предшествующему данному событию. Аналогично определяют этот показатель для всех других событий сети.
 [13]

В качестве tp ( i ] всегда принимают максимальное значение, поскольку ранний срок свершения события равен максимальному пути, предшествующему данному событию. Аналогично определяют этот показатель для всех других событий сети.
 [14]

На рис. 2.6 критический путь обозначен жирной линией. Поскольку критическим является полный путь максимальной продолжительности, его обозначают ( после расчета ранних сроков свершения событий), следуя указаниям в нижних секторах, от завершающего события к исходному. Из события 7, следуя указанию в нижнем секторе, против стрелки проводится жирная линия к событию 4, далее к 1 и нулевому.
 [15]

Страницы:  

   1

   2