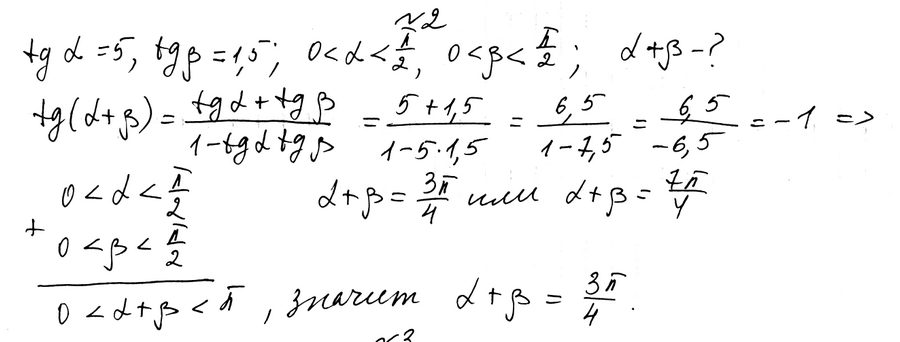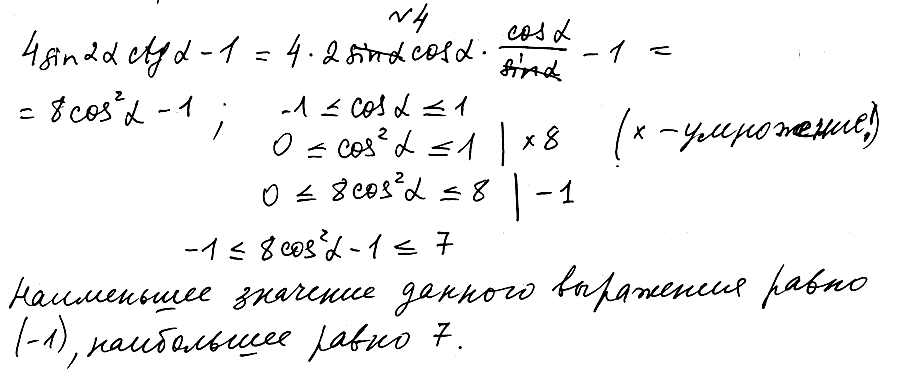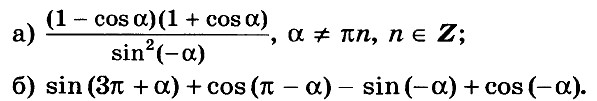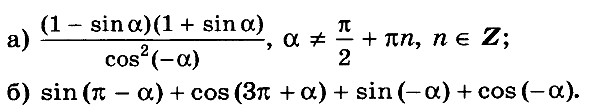Алгебра 10 класс
Контрольные работы (Базовый и углубленный уровень)
Мнемозина
Тем кто отважился все же перейти в десятый класс, предстоит пережить вскоре самое изматывающее событие в жизни — ЕГЭ. Впрочем, эти испытания не так страшны, как им приписывают. На самом деле непонятно ради чего создавать такой ажиотаж, если с аналогичными проверками школьники вполне успешно справляются в повседневности, решая задачи на контрольных. И хотя в этом году они значительно усложняются, но все же при должной подготовке с ними вполне можно справиться. В этом подросткам поможет решебник к учебнику «Алгебра. Контрольные работы 10 класс (базовый и углубленный уровень)» Глизбург, где представлен полноценный материал по всему курсу.
Основные моменты в решебнике
В данном издании представлено девять контрольных работ, каждая рассчитана на шесть вариантов. Основным аспектом является пометка времени, что поможет учащимся сориентироваться в том, сколько же им отведут на выполнение того или иного задания. ГДЗ по алгебре 10 класс Глизбург содержит проверенные и детализированные ответы по всем пунктам.
Почему его стоит применять
Если у ребенка есть математический талант — это прекрасно. А когда подростки больше тянуться к гуманитарным наукам, то данный предмет начинает представлять для них определенную проблему. Так как тематика этого курса включает в себя и тригонометрию, то воспринять все необходимые знания будет совсем непросто. Так же сложна и подготовка к контрольным работам, хотя после нее материал систематизируется таким образом, что его легко применить в дальнейшем. Поэтому стоит потратить время на то, чтобы во время настоящих испытаний не испытывать никаких затруднений. В этом начинании хорошо поможет решебник к учебнику «Алгебра. Контрольные работы 10 класс (базовый и углубленный уровень)» Глизбург. «Мнемозина», 2014 г.
Похожие ГДЗ Алгебра 10 класс
Название
Условие
Решение
Контрольная работа № 5 по алгебре для 10 класса «Соотношение между тригонометрическими функциями. Формулы сложения и их следствия» УМК Мерзляк Базовый уровень (два варианта). Дидактические материалы. 10 класс. Базовый уровень» (авт. А.Г. Мерзляк, В.Б. Полонский, Е.М.Рабинович, М.С.Якир) Цитаты использованы в учебных целях. Алгебра 10 Мерзляк КР-5 + ОТВЕТЫ только на Вариант 1
Вернуться к Списку контрольных работ по алгебре 10 класс
Тема: Соотношение между тригонометрическими функциями одного и того же аргумента. Формулы сложения и их следствия.
КР-5. Вариант 1.
КР-5. Вариант 2.
ОТВЕТЫ только на Вариант 1
№ 1. Упростите выражение:
1) (cos26a – 1)/(1 – sin26a) – tg 12a ctg 12a;
2) sin 8a cos 3a – cos 8a sin 3a;
3) (4 cos27а) / (sin 14а);
4) (sin 14а – sin 10а)/(cos 3a – cos 7a);
5) cos2(π/2 – За) – cos2(π + 3a);
6) 2 cos 8a cos 9a – cos 17a.
ОТВЕТ:
№ 2. Дано: tg a = 5, tg b = 1,5, 0 < a < π/2, 0 < b < π/2. Найдите a + b.
ОТВЕТ:
№ 3. Докажите тождество: 1) ctg 2b – ctg 4b = 1/(sin 4b);
2) ((cos (π/2 – 5a) – sin (π + 3a)) (sin (π/2 + 3a) – cos (π + 5a))) / (1 + cos (2π – 2a)) = sin 8a.
ОТВЕТ:
№ 4. Найдите наибольшее и наименьшее значения выражения 4 sin 2a ctg a – 1.
ОТВЕТ:
Вы смотрели: Контрольная работа № 5 по алгебре «Соотношение между тригонометрическими функциями. Формулы сложения и их следствия» для 10 класса УМК Мерзляк Базовый уровень. Алгебра 10 Мерзляк КР-5.
Вернуться к Списку контрольных работ по алгебре 10 класс
(с) Цитаты из пособия «Дидактические материалы. Алгебра и начала математического анализа. 10 класс. Базовый уровень» использованы в учебных целях.
Контрольная работа №1. Варианты
Контрольная работа №2. Варианты
Контрольная работа №3. Варианты
Контрольная работа №4. Варианты
Контрольная работа №5. Варианты
Контрольная работа №6. Варианты
Контрольная работа №7. Варианты
Контрольная работа №8. Варианты
Контрольная работа №9. Варианты
Чему научится школьник, применяя ГДЗ по алгебре 10 класс контрольные работы Глизбург (базовый и углубленный уровень)
Если ваш подопечный будет хотя бы иногда пользоваться нашим учебно-методическим комплексом, то он приобретет следующие компетенции:
- Научится креативно мыслить, проявлять инициативу и находчивость, активно решать поставленные задачи.
- Сможет эмоционально воспринимать все, что неразрывно связано с математикой.
- Сумеет осуществлять контроль за процессом и результатом учебной деятельности.
- Сформирует целостное мировоззрение, которое соответствует современному уровню практической науки.
- Будет критиковать не только других, но и самого себя, при этом используя конкретные факты и аргументацию.
- Сможет применять наглядное алгебраическое пособие для демонстрации на выступлениях, конференциях, коллоквиумах и в обычных беседах.
- Распознает индуктивные и дедуктивные способы рассуждения, а также сможет находить различные стратегии при решении задач.
Эти и многие другие навыки получит десятиклассник, который пользуется нашей помощью. С нашим пособием большинство детей полюбили эту точную науку и даже связали свою жизнедеятельность с ней, выбрав в качестве основного профильного предмета.
Какие темы в решебнике по алгебре 10 класс контрольно-измерительные материалы автора: Глизбург, В. И. (базовый и углубленный уровень)
На страницах нашего онлайн-пособия вы изучите следующие темы и параграфы:
- Уравнения и неравенства: иррациональные, показательные, логарифмические, равносильные, их системы.
- Корни и степени: действительный показатель, числа, арифметический корень, логарифмы (десятичные и натуральные) и их свойства, формула перехода.
- Функции: степенная, взаимообратная, сложная, дробно-линейная, показательная, логарифмическая, их свойства и графики.
- Тригонометрия: радианная мера угла, поворот точки вокруг начала координат, определение синуса, косинуса и тангенса (знаки, тригонометрические тождества, формулы сложения и приведения, сумма и разность), методы замены неизвестного и разложение на множители.
Эти сложные темы пройдет школьник и с легкостью освоит их без помощи посторонних лиц. Данная дисциплина будет даваться ему просто и легко, не вызывая никаких затруднений.
Главное, чтобы взрослые не забывали следить за тем, как работает подопечный. Дети не должны списывать готовые д/з: решебник необходим как образец выполнения заданий, а не как средство для облегчения учебы. Если десятиклассник будет «скатывать домашку», то он ничему не научится и не приобретет никаких полезных ЗУНов, которые обязан получить на выходе из школы. Поэтому важно объяснить ему, что списывать нельзя. А контролировать эти действия должны представители старшего поколения: мамы и папы, дедушки и бабушки, а также преподаватели и репетиторы. За этим нужно следить как дома, так и в стенах общеобразовательных учреждений.

Решения контрольных работ по алгебре и началам анализа из сборника для 10 класса Глизбург В. И. (под ред. А.Г. Мордковича). Профильный уровень. Варианты 1,2,3,4. — Рукопись. — 2016.
Настоящее пособие содержит решения контрольных работ из сборника «Глизбург В. И. Алгебра и начала анализа. Контрольные работы для 10 класса общеобразовательных учреждений (профильный уровень) / В. И. Глизбург ; под ред. А. Г. Мордковича. — М. : Мнемозина, 2007. — 62 с.»
Сборник контрольных работ предназначен для тех учителей математики, которые используют в своей преподавательской деятельности УМК, созданный авторским коллективом под руководством А. Г. Мордковича для изучения в 10-м классе профильной старшей школы курса алгебры и начал анализа.
Каждый вариант контрольной работы выстроен по одной и той же схеме: задания базового (обязательного) уровня — до первой черты; задания уровня выше среднего — между первой и второй чертами; задания повышенной сложности — после второй черты. Шкала оценок за выполнение контрольной работы может выглядеть так: за успешное выполнение заданий до первой черты — оценка 3; за успешное выполнение заданий базового уровня и одного дополнительного (после первой или после второй черты) — оценка 4; за успешное выполнение заданий трех уровней — оценка 5. При этом оценку не рекомендуется снижать за одно неверное решение в первой части работы (допустимый люфт).
Страницы решебника представлены в виде слайдов. Кликните на нужный слайд, чтобы прочитать содержание страницы. Как листать слайды — читайте на странице https://gdz.math-helper.ru/kak-prosmatrivat-slaydyi/
Внимание! Рукопись не проверялась, возможны ошибки!
Содержание
Контрольная работа № 1
Контрольная работа № 2
Контрольная работа № 3
Контрольная работа № 4
Контрольная работа № 5
Контрольная работа № 6
Контрольная работа № 7
Контрольная работа № 8
Контрольная работа № 9
-
ГДЗ
-
10 класс
-
Алгебра
- контрольные работы Глизбург
Автор:
Онлайн решебник контрольные работы по Алгебре для 10 класса Глизбург В.И., гдз и ответы к домашнему заданию.
ГДЗ к задачнику по алгебре за 10 класс Мордкович, Базовый и углубленный уровень можно скачать
здесь.
ГДЗ к самостоятельным работам по алгебре за 10 класс Александрова, Базовый и углубленный уровень можно скачать
здесь.
ГДЗ к задачнику по алгебре 10-11 класса Базовый уровень Мордкович можно скачать
здесь.
ГДЗ к самостоятельным работам по алгебре за 10 класс Александрова, Базовый уровень можно скачать
здесь.
ГДЗ к контрольным работам по алгебре за 10 класс Глизбург Базовый уровень можно скачать
здесь.
ГДЗ к контрольной работе №1. Варианты
ГДЗ к контрольной работе №2. Варианты
ГДЗ к контрольной работе №3. Варианты
ГДЗ к контрольной работе №4. Варианты
ГДЗ к контрольной работе №5. Варианты
ГДЗ к контрольной работе №6. Варианты
ГДЗ к контрольной работе №7. Варианты
ГДЗ к контрольной работе №8. Варианты
ГДЗ к контрольной работе №9. Варианты
Упс! Какое-то из ваших приложений или расширений браузера ломает код сайта. Пожалуйста, выключите их и перезагрузите страницу.
Дата публикации: 04 апреля 2017.
Алгебра – 10 класс. Контрольные работы с ответами к учебнику Мордковича А.Г. за 1, 2, 3, 4 четверти
Контрольные на темы: «Определение тригонометрических функций», «Свойства и графики тригонометрических функций», «Тригонометрические уравнения», «Тригонометрические функции сложения аргумента», «Правила и формулы отыскания производных», «Применение производной к исследованию функций» и др.
Контрольная работа №1 «Определение тригонометрических функций»
Вариант I
1. Вычислите функции:
| a) $sin( frac{5pi}{4})$ | б) $tg( frac{10pi}{3})$ |
| в) $cos(- frac{7pi}{3})$ | г) $ctg(- frac{9pi}{4})$ |
2. Решите следующие уравнения:
| a) $sin t = frac{sqrt{3}}{2}$ | б) $cos t = — frac{sqrt{2}}{2}$ |
3. Упростите тригонометрическое выражение:
$frac{cos(-t)}{ctg(t)} + sin(5pi +t)$
4. Докажите тождество:
$frac{(tg(t) + ctg(t))sin(t)}{tg(t)} = sin^{-1}(t)$
5. Вычисли тригонометрическую функцию:
$sqrt{75}sin(1140^{circ})+4cos(780^{circ}) — ctg^{2}(30^{circ}) $
6. Известно, что sin(t)=$frac{-2}{3},frac{3pi}{2}<t<2pi$.
Вычислите: cos(t),tg(t),ctg(t).
7. Существует ли такое число t, что выполняется равенство
sin(t)=$frac{1}{sqrt{6}-sqrt{2}}$
Вариант II
1. Вычислите функции:
| a) $sin(-frac{13pi}{4})$ | б) $tg(-frac{19pi}{6})$ |
| в) $cos(frac{13pi}{6})$ | г) $ctg(frac{7pi}{4})$ |
2. Решите следующие уравнения:
| a) $sin t = -frac{sqrt{2}}{2}$ | б) cos t = 0 |
3. Упростите тригонометрическое выражение:
$frac{sin(-t)}{tg(-t)} — cos(-2pi+t)$
4. Докажите тождество:
$frac{(tg(t)+ctg(t))cos(t)}{ctg(t)} =cos^{-1}(t)$
5. Вычисли тригонометрическую функцию:
$2sin(750^o )-sqrt{3} cos(930^o )+frac{tg^2(60^{circ})}{2} $
6. Известно, что cos(t)=$frac{2}{3},0<t<frac{π}{2}$.
Вычислите: sin(t),tg(t),ctg(t).
7. Существует ли такое число t, что выполняется равенство
sin(t)=$frac{1}{sqrt{11}-sqrt{15}}$
Ответы на контрольную работу №1
Контрольная работа №2 «Свойства и графики тригонометрических функций»
Вариант I
1. Найдите наименьшее и наибольшее значение функции y=sin(x), на отрезке [$frac{pi}{3};frac{4pi}{3}$].
2. Упростите тригонометрические функции:
а) $cos^2 (2π+t)+sin^2(frac{3pi}{2}-t)$;
б) $frac{sin(-t)tg(frac{pi}{2}+t)}{sin(frac{pi}{2}-t)}$.
3. Решите уравнение: $sin(t-frac{pi}{2})-cos(2π+t)=sqrt{3}$.
4. Постройте график функции: $y=cos(x+frac{pi}{4})-2$.
5. Постройте график функции: $y=-3sin(2x)$.
6. Известно, что $f(x)=-4x^2+4x-4$. Докажите, что $f(sin(x))=-8+4cos^2 (x)+4sin(x)$.
Вариант II
1. Найдите наименьшее и наибольшее значение функции y=cos(x), на отрезке [$frac{3pi}{4};frac{11pi}{6}$].
2. Упростите тригонометрические функции:
а) $cos^2 (π-t)+sin^2(t-pi)$;
б) $frac{cos(t)ctg(frac{pi}{2}+t)}{cos(frac{pi}{2}+t)}$.
3. Решите уравнение: $sin(pi+t) + cos(frac{pi}{2})+t)=sqrt{2}$.
4. Постройте график функции: $y=sin(x+frac{pi}{4})-3$.
5. Постройте график функции: $y=2cos(frac{x}{3})$.
6. Известно, что $f(x)=-4x^2+3x-4$. Докажите, что $f(cos(x))=-4sin^2 (x)+3cos(x).$
Ответы на контрольную работу №2
Контрольная работа №3 «Тригонометрические уравнения»
Вариант I
1. Решите уравнения:
$ а) –2sin(x)+sqrt{3}=0; б)cos(3x+frac{pi}{3})-1=0;$
$ в)-2cos^2 (x)-5sin(x)-1=0; с)sin^2 (x)+4sin(x)cos(x)-5cos^2 (x)=0;$
2. Решите уравнение:
$ 2sin^2 (x)-8sin(x)cos(x)+7cos^2 (x)=1$
3. Найдите корни уравнения: sin(4x)=cos(4x), принадлежащие отрезку [-1 ; 3].
Вариант II
1. Решите уравнения:
$ а) 6sin(x)+frac{sqrt{3}}{2}=0; б)sin(2x+frac{pi}{4})+1=0;$
$ в)2sin^2 (x)-6cos(x)+6=0; с)cos^2 (x)-2sin(x)cos(x)-3sin^2 (x)=0;$
2. Решите уравнение:
$ 2sin^ (x)-5sin(x)cos(x)-8cos^2 (x)=-1$
3. Найдите корни уравнения: sin(3x)=$sqrt{3}$cos(3x), принадлежащие отрезку [-2 ; 4].
Ответы на контрольную работу №3
Контрольная работа №4 «Тригонометрические функции сложения аргумента»
Вариант I
1. Найдите значения выражений:
а) $sin(53°)cos(23°)-cos(53°)sin(23°)$;
б) $cos(frac{pi}{8})cos(frac{pi}{24})-sin(frac{pi}{8})sin(frac{pi}{24})$.
2.Упростите выражения:
а) $sin(α+β)-sin(β)cos(α)$;
б) $cos(frac{pi}{4}-x)-frac{sqrt{2}}{2}sin(x)$.
3. Докажите тождество:
$sin(α+β)+cos(α-β)=(sin(α)+cos(α))(cos(β)+sin(β))$.
4. Решите уравнение:
$sin(4x)cos(2x)+cos(4x)sin(2x)=0$.
5. Зная, что $sin(α)=frac{5}{13},frac{pi}{2}<α<pi$, найдите $tg(α-frac{pi}{4}).$
6. Известно, что $cos(frac{pi}{3}-t)-cos(frac{pi}{3}+t)=q$.
Найдите $cos(frac{pi}{3}-t)×cos(frac{pi}{3}+t)$.
Вариант II
1. Найдите значения выражений:
а) $sin(83°)cos(52°)+cos(83°)sin(52°)$;
б) $cos(frac{3pi}{2})cos(frac{2pi}{3})-sin(frac{3pi}{2})sin(frac{2pi}{3}).$
2.Упростите выражения:
а) $cos(z+y)-sin(z)cos(y)$;
б) $sin(x -frac{pi}{4})+frac{sqrt{2}}{2}cos(x)$.
3. Докажите тождество:
$sin(α-β)+cos(α+β)=(sin(α)+cos(α))(cos(β)-sin(β))$.
4. Решите уравнение:
$cos(6x)cos(2x)-sin(6x)sin(2x)=0$.
5. Зная, что $cos(α)=-frac{5}{13},pi<α<frac{3pi}{2}$, найдите $tg(α+frac{pi}{4})$.
6. Известно, что $sin(frac{pi}{4}-t)-sin(frac{pi}{4}+t)=q$.
Найдите $sin(frac{pi}{4}-t)×sin(frac{pi}{4}+t)$.
Ответы на контрольную работу №4
Контрольная работа №5 «Формулы тригонометрии»
Вариант I
1. Упростите выражение:
$frac{2cos(t)}{(sin(2t)}-sin(t)$.
2.Решите уравнение:
$cos(8x)=cos(4x)$.
3. Докажите тождество:
$2cos^2 (60^o-3α)-frac{sqrt{3}}{2} sin(6α)-sin^2 (3α)=frac{1}{2}$.
4.Вычислите:
$cos(85^o )+sin(125^o )-cos(25^o)$.
5.Решите уравнение:
$-sqrt{3} sin(x)-cos(x)=1$.
6. Решите уравнение:
$cos(8x)+cos(4x)+2sin^2 (x)=1$.
Вариант II
1. Упростите выражение:
$frac{2sin(t)}{(sin(2t)}-cos(t)$.
2.Решите уравнение:
sin(9x)=sin(5x).
3. Докажите тождество:
$4cos^2 (45^o-4α)-2sin(8α)=2$.
4.Вычислите:
$sin(40^o )+cos(170^o )+sin(20^o)$.
5.Решите уравнение:
$-sqrt{3} sin(x)+cos(x)=-1$.
6. Решите уравнение:
$sin(5x)-2cos^2(x)+sin(9x)=-1$.
Ответы на контрольную работу №5
Контрольная работа №6 «Правила и формулы отыскания производных»
Вариант I
1. Найдите производные функций: а) $y=2x^4$; б) $y=-1$; в) $y=-frac{3}{2x}$; г) $y=7x-10$;
д) $y=3sqrt{x}+frac{sin(x)}{2}$.
2. Найдите производные функций: а) $y=frac{x}{cos(x)}$; б) $y=frac{x}{tg(x)}$; в) $y=(4x-6)^5$.
3. Вычислите $f'(frac{π}{4})$, если $f(x)=3cos(x)+4x^2-2πx+5$.
4. Прямолинейное движение точки описывается законом $t^7-3t^3$. Найдите ее скорость в момент времени $t=2c$.
5. Найдите все значения x, при которых выполняется неравенство $f'(x)≤0$, если $f(x)=4,5x^2-12x^3$.
6. Найдите все значения x, при которых выполняет равенство $f'(x)=0$, если $f(x)=sin(2x)+sqrt{2}x$, $xϵ[pi;5pi]$.
Вариант II
1. Найдите производные функций: а) $y=frac{3x^4}{2}$; б) $y=-2$; в) $y=-frac{x}{4}+5cos(x)$;
г) $y=-3x-4$; д) $y=frac{10}{x}$.
2. Найдите производные функций: а) $y=frac{x}{cos(x)}$; б) $y=frac{x}{ctg(x)}$; в) $y=(6x+1)^8$.
3. Вычислите $f'(frac{pi}{4})$, если $f(x)=4sin(x)+0,5x^2+frac{pi}{4}x-3$.
4. Прямолинейное движение точки описывается законом $t^4-15t^2$. Найдите ее скорость в момент времени $t=4c$.
5. Найдите все значения x, при которых выполняется неравенство $f'(x)<0$, если $f(x)=x^2-5x^3$.
6. Найдите все значения x, при которых выполняет равенство $f'(x)=0$, если $f(x)=2cos(2x)-2sqrt{2}x$, $xϵ[-pi;3pi]$.
Ответы на контрольную работу №6
Контрольная работа №7 «Применение производной к исследованию функций»
Вариант I
1. Дана функция $y=2x^3-6x^2+1$. Найдите:
а) промежутки возрастания и убывания функции;
б) точки экстремума;
в) наибольшее и наименьшее значение функции на отрезке [-1;4].
2. Постройте график функции: $y=2x^3-6x^2+1$.
3.Составьте уравнение касательной к графику функции $y=frac{12}{x}$ в точке $x=6$.
4.Площадь прямоугольного участка 196 м2. При каких размерах участка длина окружающего забора будет наименьшей.
5. Постройте график функции: $y=frac{2x^2-3}{2x^2+3}$.
Вариант II
1. Дана функция $y=2x^3+6x^2-1$. Найдите:
а) промежутки возрастания и убывания функции;
б) точки экстремума;
в) наибольшее и наименьшее значение функции на отрезке [-3;1].
2. Постройте график функции: $y=2x^3+6x^2-1$.
3.Составьте уравнение касательной к графику функции $y=frac{15}{x}$ в точке $x=3$.
4.Площадь прямоугольного треугольника 8 см2. Найдите наименьшее значение площади квадрата, построенного на гипотенузе треугольника..
5. Постройте график функции: $y=frac{3x^2-6}{3x^2+6}$.
Ответы на контрольную работу №7
Ответы на контрольную работу №1 «Определение тригонометрических функций»
Вариант I
1. а) $-frac{sqrt{2}}{2}$; б) $sqrt3$; в) 0,5: г) -1.
2. а) $frac{π}{3}+2πn$; $frac{2π}{3}+2πn$.
б) $±frac{π}{4}+2πn$.
3. 0.
4. $frac{(tg(t)+ctg(t))sin(t)}{tg(t)}$=$frac{(frac{sin(t)}{cos(t)}+frac{cos(t)}{sin(t)} )sin(t)}{frac{sin(t)}{cos(t)}}$=$frac{frac{1}{sin(t)cos(t)}sin(t)}{frac{sin(t)}{cos(t)}}$=$frac{1}{sin(t)}=sin^{-1}(t)$.
5. 6,5.
6. $cos(t)=frac{sqrt{5}}{3}$; $tg(t)=-frac{2}{sqrt{5}}$; $ctg(t)=-frac{sqrt{5}}{2}$.
7. Существует.
Вариант II
1. а) $frac{sqrt{2}}{2}$; б) $-frac{1}{sqrt{3}}$; в) $frac{sqrt{3}}{2}$; г) -1.
2. а) $-frac{π}{4}+2πn$ и $-frac{3π}{4}+2πn$; б) $frac{π}{2}+πn$.
3. 0.
4. $frac{(tg(t)+ctg(t))cos(t)}{ctg(t)}$=$frac{(frac{sin(t)}{cos(t)}+frac{cos(t)}{sin(t)})cos(t)}{frac{cos(t)}{sin(t)}}$=$frac{frac{1}{sin(t)cos(t)}cos(t)}{frac{cos(t)}{sin(t)}}$=$frac{1}{cos(t)}=cos^{-1}(t)$.
5. 4.
6. $sin(t)=frac{sqrt{5}}{3}$; $tg(t)=frac{sqrt{5}}{2}$; $ctg(t)=frac{2}{sqrt{5}}$.
7. Не существует.
Ответы на контрольную работу №2 «Свойства и графики тригонометрических функций»
Вариант I
1. Наибольшее значение: 1. Наименьшее значение: $-frac{sqrt{3}}{2}$.
2. а) $2cos^2(t)$; б) 1.
3. $frac{±5π}{6}+2πn$.
4.
5.
6. $f(sin(x))=-4sin^2(x)+4sin(x)-4=-4(1-cos^2(x))+4sin(x)-4=-4+4cos^2(x)+4sin(x)$.
Вариант II
1. Наименьшее: -1. Наибольшее: $frac{sqrt{3}}{2}$.
2. а) 1; б) 1.
3. $frac{-π}{4}+2πn$ и $frac{-3π}{4}+2πn$.
4.
5.
6. $f(cos(x))=4cos^2(x)+3cos(x)-4=4(1-sin^2(x))+3cos(x)-4=$
$=4-4sin^2(x)+3cos(x)-4=-4sin^2(x)+3cos(x)$.
Ответы на контрольную работу №3 «Тригонометрические уравнения»
Вариант I
1. а) $frac{π}{3}+2πn$ и $frac{2π}{3}+2πn$; б) $frac{2πn}{3}-frac{π}{9}$; в)$frac{-π}{6}+2πn$ и $frac{-5π}{6}+2πn$; г) $-arctg(5)+πn$ и $frac{π}{4}+πn$.
2. $arctg(frac{8±sqrt{40}}{2})+πn$.
3. $frac{-3π}{16}$; $frac{π}{16}$; $frac{5π}{16}$.
Вариант II
1. а) $(-1)^narcsin(frac{sqrt{3}}{12})+πn$; б) $frac{-3π}{8}+2πn$; в) $2πn$; г) $arctg(frac{1}{3})+πn$ и $frac{-π}{4}+πn$.
2. $arctg(frac{5±sqrt{109}}{6})+πn$.
3. $frac{-5π}{9}$; $frac{-2π}{9}$; $frac{π}{9}$; $frac{4π}{9}$; $frac{7π}{9}$; $frac{10π}{9}$.
Ответы на контрольную работу №4 «Тригонометрические функции сложения аргумента»
Вариант I
1. а) 0,5; б) $frac{sqrt{3}}{2}$.
2. а) $sin(α)cos(β)$; б) $frac{sqrt{2}}{2}cos(x)$.
3. $sin(α+β)+cos(α-β)=sin(α)cos(β)+sin(β)cos(α)+cos(α)cos(β)+sin(α)sin(β)=$
$=sin(α)(cos(β)+sin(β))+cos(α)(sin(β)+cos(β))=(sin(α)+cos(α))(cos(β)+sin(β))$.
4. $frac{πn}{6}$.
5. $-2frac{3}{7}$.
6. $frac{1}{4}-frac{q^2}{3}$.
Вариант II
1. а) $frac{sqrt{2}}{2}$; б) $-frac{sqrt{3}}{2}$.
2. а) $cos(y)(cos(z)-sin(z))-sin(z)sin(y)$; б) $frac{sqrt{2}}{2}sin(x)$.
3. $sin(α-β)+cos(α+β)=sin(α)cos(β)-cos(α)sin(β)+cos(α)cos(β)-sin(α)sin(β)=$
$=sin(α)(cos(β)-sin(β))-cos(α)(sin(β)-cos(β))=(sin(α)+cos(α))(cos(β)-sin(β))$.
4. $frac{π}{16}+frac{πn}{8}$.
5. $–2frac{3}{7}$.
6. $frac{q^2-1}{2}$.
Ответы на контрольную работу №5 «Формулы тригонометрии»
Вариант I
1. $cos(t)*ctg(t)$.
2. $frac{πn}{6}$ и $frac{πn}{2}$.
3. $2cos^2(60^o-3α)-frac{sqrt{3}}{2}sin(6α)-sin^2(3α)=2(cos(60^o)cos(3α)+sin(60^o)sin(3α))^2-frac{sqrt{3}}{2}sin(6α)-sin^2(3α)=$
$=2(frac{1}{2}cos(3α)+frac{sqrt{3}}{2})sin(3α))^2-frac{sqrt{3}}{2}sin(6α)-sin^2(3α)=$
$=2(frac{1}{4}cos^2 (3α)+frac{sqrt{3}}{2}cos(3α)sin(3α)+frac{3}{4}sin^2(3α))-frac{sqrt{3}}{2}sin(6α)-sin^2(3α)=$
$=frac{1}{2}cos^2(3α)+sqrt{3}cos(3α)sin(3α)+frac{3}{2}sin^2(3α)-frac{sqrt{3}}{2}sin(3α)cos(3α)-sin^2(3α)=frac{1}{2}(cos^2(3α)+sin^2(3α))=frac{1}{2}$.
4. 0.
5. $frac{-π}{3}+2πn$ и $-π+2πn$.
6. $frac{π}{4}+frac{πn}{2}$ и $±frac{π}{18}+frac{πn}{3}$.
Вариант II
1. $tg(t)*sin(t)$.
2. $frac{πn}{2}$ и $frac{π}{14}+frac{πn}{7}$.
3. $4cos^2(45^o-4α)-2sin(8α)=4(cos(45^o)cos(4α)+sin(45^o)sin(4α))^2-2sin(8α)=$
$=4(frac{1}{2}cos^2(4α)+2*frac{1}{sqrt{2}}*frac{1}{sqrt{2}}*cos(4α)sin(4α)+frac{1}{2}sin^2 (4α)-4sin(4α)cos(4α)=$
$=4(frac{1}{2}+cos(4α)sin(4α))-4sin(4α)cos(4α)=2$.
4. 0.
5. $frac{–4π}{3}+2πn$.
6. $frac{π}{42}+frac{2πn}{7}$ и $frac{5π}{42}+frac{2πn}{7}$ и $frac{π}{4}+frac{πn}{2}$.
Ответы на контрольную работу №6 «Правила и формулы отыскания производных»
Вариант I
1. а) $8x^3$; б) 0; в) $frac{3}{2x^2}$; г) 7; д) $frac{3}{2sqrt{x}}+frac{cos(x)}{2}$.
2. а) $frac{cos(x)+x*sin(x)}{cos^2(x)}$; б) $frac{sin(x)cos(x)-x}{sin^2(x)}$; в) $20(4x-6)^4$.
3. $-frac{3}{sqrt{2}}$.
4. 412.
5. $(-∞;0]∪[frac{1}{4};+∞)$.
6. $frac{11π}{8}$; $frac{13π}{8}$; $frac{19π}{8}$; $frac{21π}{8}$; $frac{27π}{8}$; $frac{29π}{8}$; $frac{35π}{8}$; $frac{37π}{8}$.
Вариант II
1. а) $6x^3$; б) 0; в) $frac{-1}{4}-5sin(x)$; г) -3; д) $frac{-10}{x^2}$.
2. а) $frac{cos(x)+x*sin(x)}{cos^2(x)}$; б) $frac{cos(x)sin(x)+x}{cos^2(x)}$; в) $48(6x+1)^7$.
3. $2sqrt{2}+frac{π}{2}$.
4. 136.
5. $(-∞;0)∪(frac{2}{15};+∞)$.
6. $-frac{3π}{8}$; $-frac{π}{8}$; $frac{5π}{8}$; $frac{7π}{8}$; $frac{13π}{8}$; $frac{15π}{8}$; $frac{21π}{8}$; $frac{23π}{8}$.
Ответы на контрольную работу №7 «Применение производной к исследованию функций»
Вариант I
1. а) возрастает — $(-∞;0)∪(2;+∞)$, убывает — (0;2); б) точка минимума: 2, точка максимума: 0;
в) наибольшее значение: 1, наименьшее значение: -7.
2.
3. $y=frac{-x}{3}+4$.
4. 14.
5.
Вариант II
1. а) возрастает — $(-∞;-2)∪(0;+∞)$, убывает- (-2;0); б) точка минимума: 0, точка максимума: -2;
в) наибольшее значение: 7, наименьшее значение: -1.
2.
3. $y=-frac{5}{3}x+10$.
4. $2^{frac{3}{4}}$.
5.
Контрольная работа № 5 по алгебре в 10 классе с ответами. Используется при работе по УМК Никольский. Цитаты из пособия «Алгебра и начала математического анализа. Дидактические материалы. 10 класс : базовый и углубленный уровни / Потапов, Шевкин» использованы в учебных целях. Ответы адресованы родителям. Алгебра 10 Никольский Контрольная 5 + ответы.
Алгебра и начала анализа. 10 класс
Контрольная работа № 5 (Никольский)
К-5. Вариант 3 (транскрипт)
- Вычислите: a) sin 30° + √6 cos 45° sin 60° – tg 30° ctg 150° + ctg 45°; б) cos π/3 – √2 sin 3π/4 + √3 tg π/3.
- Упростите выражение:
- Вычислите: а) (sin2 а – cos2 а)2+ 4 sin2 а cos2 а; б) tg a + ctg a, если sin a cos а = 0,3.
- Найдите все такие углы а, для каждого из которых выполняется равенство: а) sin a = –√3/2; б) cos a = √2/2; в) tg a = √3/3; г) ctg a = –√3.
- * Вычислите: а) tg2 a + ctg2 а, если tg a + ctg a = 4;
б) 1 – 2/(tg a + ctg a), если cos a – sin a = –1/3. - * Вычислите arcsin 1 – arccos √3/2 – (arctg (–√3/3)) / (arcctg (–√3).
- * Некоторое расстояние планировали проехать с постоянной скоростью, а проехали расстояние на 40% большее и со скоростью на 60% большей. На сколько процентов время движения оказалось меньше запланированного?
К-5. Вариант 4 (транскрипт)
- Вычислите: а) cos 60° – √6 cos 30° sin 45° + ctg 30° tg 150° – tg 45°;
б) sin π/6 + √2 cos 3π/4 – √3 ctg π/3. - Упростите выражение:
- Вычислите: а) (cos2 a – sin2 a)2 + 4 sin2 a cos2 a; б) tg a +ctg a, если sin a cos a = 0,6.
- Найдите все такие углы а, для каждого из которых выполняется равенство:
a) sin a = √2/2; б) cos a –1/2; в) tg a = –√3/3; г) ctg a = √3. - * Вычислите: а) tg2 a + ctg2 а, если tg a – ctg a = – 4; б) 1 – 2/(tg a + ctg a), если cos a + sin a = 1/3.
- * Вычислите arcsin √3/2 – arccos 1 + (arctg (–√3)) / (arcctg (–√3/3).
- * Некоторое расстояние планировали проехать с постоянной скоростью, а проехали расстояние на 40% большее и со скоростью на 75% большей. На сколько процентов время движения оказалось меньше запланированного?
Ответы на контрольную работу
Вернуться к Списку контрольных работ по алгебре в 10 классе (Никольский)
Вы смотрели: Алгебра и начала математического анализа. 10 класс. Контрольная работа с ответами. Используется при работе по УМК Никольский. Цитаты из пособия Потапова и Шевкина использованы в учебных целях. Ответы адресованы родителям.
Алгебра 10 Никольский Контрольная 5 + ответы.

/title.jpg)
/conditions/Kontrolnaya-rabota-1-Varianty/1.jpg)
/exercise/Kontrolnaya-rabota-1-Varianty/1.jpg)