Линейный коэффициент корреляции
Краткая теория
Под теснотой связи между
двумя величинами понимают степень сопряженности между ними, которая
обнаруживается с изменением изучаемых величин. Если каждому заданному
значению
соответствуют
близкие друг другу значения
, то связь считается тесной (сильной); если
же значения
сильно
разбросаны, то связь считается менее тесной.
Рассмотрим наиболее важный
для практики и теории случай линейной зависимости вида:
При тесной корреляционной
связи корреляционное поле представляет собой более или менее сжатый эллипс. Две
корреляционные зависимости переменной
от
приведены на рисунке.
Очевидно, что в случае (а)
зависимость между переменными менее тесная, чем в случае (б), так как точки
корреляционного поля (а) дальше отстоят от линии регрессии, чем точки поля (б).
Перейдем к оценке тесноты
линейной корреляционной зависимости. Для показателя тесноты связи нужная такая
стандартная система единиц измерения, в которой данные по различным
характеристикам оказались бы сравнимы между собой. Статистика знает такую
систему единиц. Эта система использует в качестве единицы измерения переменной
ее среднее квадратическое отклонение
.
Учтем, что
и запишем
уравнение парной линейной зависимости
в эквивалентном виде:
В этой системе величина:
показывает, на сколько
величин
изменится
в среднем
, когда
увеличится
на одно
.
Величина
является
показателем тесноты связи и называется линейным коэффициентом корреляции. Коэффициент
корреляции, определяемый по выборочным данным, называется выборочным коэффициентом корреляции.
Если
, то корреляционная связь между переменными
называется прямой, если
– обратной.
Приведем другие модификации
формулы для расчета линейного коэффициента корреляции:
или
Наиболее часто для расчета
используют формулу, получаемую простыми преобразованиями:
По этой формуле
находится
непосредственно из данных наблюдений и на значении
не
скажутся округления данных, связанных с расчетом средних и дисперсий.
Линейный выборочный
коэффициент корреляции
(при
достаточно большом объеме выборки
) обладает следующими свойствами:
-
Коэффициент корреляции
принимает значения на отрезке
, т.е.
. При этом, чем ближе по модулю
к
единице – тем теснее связь.
При
корреляционная
связь представляет собой линейную функциональную зависимость. При этом все
наблюдаемые значения располагаются на прямой линии.
При
линейная
корреляционная связь отсутствует. При этом линия регрессии параллельна оси
.
Расчет линейного коэффициента корреляции предполагает, что
переменные
и
распределены нормально. В других случаях
(когда распределения
и
отклоняются от нормальных) линейный
коэффициент корреляции не следует рассматривать как строгую меру взаимосвязи
переменных.
Пример решения задачи
Задача
Компания,
занимающаяся продажей радиоаппаратуры, установила на видеомагнитофон
определенной модели цену, дифференцированную по регионам. Следующие данные
показывают цены на видеомагнитофон в 10 различных регионах о соответствующее им
число продаж:
|
Число продаж, шт. |
420 | 380 | 350 | 400 | 440 | 380 | 450 | 425 | 430 | 480 |
| Цена, тыс.руб. | 5.6 | 6.0 | 6.5 | 6.0 | 5.0 | 6.4 | 4.5 | 5.0 | 5.7 | 4.4 |
Рассчитайте
выборочный коэффициент линейной корреляции и проверьте его значимость
при
.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Составим
расчетную таблицу:
Вычислим
линейный коэффициент корреляции:
Вывод
Связь
между числом продаж и ценой очень тесная, обратная – с уменьшением цены
увеличивается объем продаж.
Проверим
значимость коэффициента корреляции:
По таблице критических точек t-критерия Стьюдента (по уровню значимости
и числу степеней свободы
) находим:
— коэффициент корреляции значим.
Кроме этой задачи на другой странице сайта есть еще
задача на расчет коэффициента корреляции, коэффициента детерминации, построение линии линейной регрессии и корреляционного поля.
Для приведенных исходных данных
постройте диаграмму рассеяния и
определите по ней характер зависимости.
Рассчитайте выборочный коэффициент
корреляции Пирсона, проверьте его
значимость при α=0,05. Запишите уравнение
регрессии и дайте интерпретацию
полученных результатов.
Компания, занимающаяся продажей
радиоаппаратуры, установила на
видеомагнитофон определенной модели
цену, дифференцированную по регионам.
Исследуйте зависимость объема продаж
(Y, шт.) от цены (Х,
тыс. руб.) по выборочным данным из 8
регионов.
|
Х |
5,5 |
6,0 |
6,5 |
6,0 |
5,0 |
6,5 |
4,5 |
5,0 |
|
Y |
420 |
380 |
350 |
400 |
440 |
380 |
450 |
420 |
Решение:
Факторной переменной в
нашей задаче является Х – цена
видеомагнитофона, откликом является Y
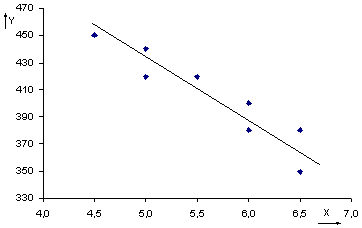
– объем продаж. Построим диаграмму
рассеяния (рисунок 7.1) по имеющимся
данным.
Рисунок 7.1 – Диаграмма рассеяния.
По виду диаграммы есть основания
предполагать достаточно сильную
линейную отрицательную зависимость
объема продаж от цены.
Для расчета коэффициентов регрессии
по формулам найдем средние значения:
,
,
найдем несмещенные оценки дисперсий:
,
,
и оценку коэффициента корреляции
Пирсона:
Коэффициент Пирсона достаточно близок
к единице и имеет отрицательное значение,
значит можно утверждать об отрицательной
связи между объемом продаж и ценой на
товары.
Найдем коэффициенты b0
и b1 уравнения
регрессии:
где
— средние значения переменных Х и
Y, рассчитанные по
выборке;
— несмещенные оценки дисперсий Х и
Y;
— оценка коэффициента корреляции Пирсона.
Таким образом, уравнение регрессии Y
на Х имеет вид
Коэффициент b1
характеризует наклон линии регрессии
и значение
показывает, что при увеличении Х на
единицу ожидаемое значение Y
уменьшается на 37,25711. Полученная
регрессионная модель указывает на то,
что каждое увеличение цены видеомагнитофона
на 1 тысячу рублей уменьшает объем их
продаж на 37,25711. Отсюда b1
может интерпретироваться как изменение
объема продаж, который изменяется в
зависимости от изменения цены на
видеомагнитофоны.
Свободный член b0
в уравнении – это значение Y
при Х=0. Поскольку маловероятно, что
цена видеомагнитофона равна нулю, то
можно рассматривать b0
как меру влияния на величину объема
продаж других факторов, не включенных
в уравнение регрессии. Это влияние можно
объяснить и с помощью коэффициента
детерминации:
,
Для линейной модели коэффициент
характеризует долю объясняемого моделью
разброса экспериментальных данных. В
нашем примере модель учитывает 67,23%
изменения выручки
магазина. И 32,7% разброса объясняются
факторами, не включенными в уравнение
регрессии.
Коэффициент эластичности для нашей
модели вычисляем по формуле:
,
то есть при увеличении средней цены на
видеомагнитофон на 1% объем их продаж в
среднем уменьшается на 0,517%.
Так как исходная выборка малого объема,
проверим значимость коэффициента
корреляции. Основная гипотеза Н0
состоит в том, что коэффициент корреляции
не значим Н0:
то есть между переменными Х и Y
нет линейной связи. Альтернативная
гипотеза Н1:
— коэффициент корреляции значим, и
переменные Х и Y
связаны отрицательной линейной
зависимостью.
Наблюдаемое значение статистики К
равно:
Согласно заданному уровню значимости
α=0,05 определим границу критической
области по таблице распределения
Стьюдента. По виду альтернативной
гипотезы заключаем, что критическая
область является левосторонней: (-∞;
—Ккр]. Значение Ккр
находим по таблице распределения
Стьюдента:
.
Наблюдаемое значение
попадает в критическую область (-∞;
-1,94], поэтому основную гипотезу следует
отвергнуть в пользу альтернативной:
связь между переменными Х и Y
значима.
Данные наблюдений на уровне значимости
α=0,05 говорят о том, что объем продаж
видеомагнитофонов в среднем линейно
убывает при увеличении цены на него.
Проводится исследование зависимости числа продаж видеомагнитофонов (y) от цены (х) по статистическим данным выборки.
1)
Зависимая переменная y – число продаж, шт.
Фактор х – цена видеомагнитофона, у.е.
Диаграмма рассеивания:
По диаграмме можно сделать вывод, что между признаками наблюдается линейная убывающая связь.
Эта связь, то есть зависимость у от х описывается уравнением
у=b0+b1*x
Для оценки коэффициентов уравнения b0 и b1 применяют метод наименьших квадратов, он состоит в минимизации суммы квадратов отклонений фактических значений зависимой переменной yi от расчетных yi
yi-yi2=yi-(b0+b1xi)2b0,b1min
Чтобы решить задачу минимизации, то есть рассчитать b0 и b1, нужно составить и решить относительно b0 и b1 систему нормальных уравнений
nb0+b1∑xi = ∑yib0∑xi+b1∑xi2=∑xiyi
Решением системы являются
b1=∑xiyi-1n∙∑xi·∑yi∑xi2-1n∑xi2
b0=∑yin-b1∙∑xin
Расчеты проведены в Excel:
Уравнение регрессии
у=626,89-40,79*x
Коэффициент b1=-40,79 показывает, что при увеличении цены на видеомагнитофон (за 1 шт.) на 1 у.е
. количество проданных единиц (число продаж y) снижается на 40,79 шт. в среднем.
Коэффициент b0=626,89 интерпретировать можно так: если бы цена на видеомагнитофон (за 1 шт.) была равна 0 у.е., мы бы “продали” 626,89 штук в среднем (то есть отдали бы даром).
2)
Найдем прогнозные значения yi и построим теоретическую линию регрессии.
Можно сделать вывод о том, что модель адекватна исходным данным.
3)
Рассчитаем следующие суммы квадратов
Общая сумма квадратов (общая дисперсия)
Qобщ=yi-y2
Сумма квадратов остатков (остаточная дисперсия)
Qост=yi-yi2
Сумма квадратов, объясненная регрессией
Qрегр=yi-y2
Коэффициент детерминации показывает долю дисперсии зависимой переменной у, объясненную уравнением и является мерой адекватности построенной модели.
Формула расчета
R2=1-QостQобщ
R2=1-1611,917200=0,7761
77,61% дисперсии количества проданных единиц видеомагнитофонов объяснено построенной моделью. Так как процент высокий, модель адекватно описывает исходные данные.
Линейный коэффициент корреляции является мерой линейной зависимости между зависимой переменной у и фактором х.
Формула расчета
R=R2
R=0,7761=0,88
Так как R > 0,7 то связь между признаками сильная.
4)
Для оценки значимости уравнения регрессии рассчитаем F-статистику
Fнабл=Qрегр1Qост(n-2)=5588,091611,91/6=20,8
Критическое значение распределения Фишера при уровне значимости = 0,05 и числе степеней свободы k1 = 1 и k2 = n – 2 найдем функцией Excel FРАСПОБР с параметрами (0,05;1;8-2)
Fкрит=5,987
Так как Fнабл > Fкрит, то уравнение признается значимым с вероятностью 95%.
Статистическая значимость коэффициентов регрессии проверяется критерием Стьюдента.
Сначала вычисляются стандартизированные ошибки коэффициентов регрессии
Sb0=Qостn-2*x2n*x-x2
Sb1=Qостn-2*1(x-x)2
Далее t-статистики коэффициентов
tb0=b0Sb0
tb1=b1Sb1
Далее критическое значение распределения Стьюдента при уровне значимости = 0,05 и числе степеней свободы k = n – 2 функцией Excel
tкрит= СТЬЮДРАСПОБР(0,05; 8-2)
Расчеты с помощью Excel
Так как расчетные t-статистики по модулю больше чем критическое значение распределения Стьюдента:
tb0>tкрит
tb1>tкрит
то оба коэффициента b0 и b1 значимы с вероятностью 95%.
Интервальные оценки генеральных параметров β0 и β1
b0-tкрит*Sb0<β0<b0+tкрит*Sb0
b1-tкрит*Sb1<β1<b1+tкрит*Sb1
С доверительной вероятностью 95% параметры попадают в интервалы:
β0∈(504,34;749,44)
β1∈-62,67;-18,91
5)
По уравнению у=626,89-40,79*x
точечный прогноз зависимой переменной y (число проданных видеомагнитофонов, шт.) при цене x* = 5,75 у.е.
y*=626,89-40,79*5,75=392,35
Стандартная ошибка прогноза
Sy*=Qостn-2∙1+1n+(x*-x)2(x-x)2
Интервальный прогноз зависимой переменной Y
y*-tкрит*Sy*<Y*<y*+tкрит*Sy*
С доверительной вероятностью 95% число проданных видеомагнитофонов Y при цене 5,75 у.е


Подборка по базе: Примеры заданий на развитие функциональной.docx, Бланк титульного листа для практических заданий.docx, задачи решение.docx, Готовое решение АД.docx, Соколова только решение 2 практ.docx, (1-5 заданий) — Контрольная работа №6 — Ряды.pdf, (1-5 заданий) — Контрольная работа №8 -ТФКП.pdf, Ситуационные задачи с решением по уголовному процессуальному пра, (1-5 заданий)-Контрольная работа №3-Неопределенные интегралы.pdf, (1-6 заданий)-Контрольная работа №1-Матричная алгебра.pdf
Задача по эконометрике с решением. Выполнена в https://www.matburo.ru/
©МатБюро – Решение заданий высшей математики, экономики, бухучета
Решение задачи по эконометрике (парная регрессия)
Задание
- Постройте поле корреляции результативного и факторного признаков.
- Определите параметры уравнения парной линейной регрессии. Дайте интерпретацию найденных параметров и всего уравнения в целом.
- Постройте теоретическую линию регрессии, совместив ее с полем корреляции. Сделайте выводы.
- Рассчитайте линейный коэффициент корреляции и поясните его смысл. Определите коэффициент детерминации и дайте его интерпретацию.
- С вероятностью 0,95 оцените статистическую значимость коэффициента регрессии и уравнения регрессии в целом. Сделайте выводы.
- С вероятностью 0,95 постройте доверительный интервал для прогноза оценки yi и
доверительный интервал генерального значения
ˆyген.( x = 5,75).
- Определите значение коэффициента эластичности и объясните его.
Компания, занимающаяся продажей радиоаппаратуры, установила на видеомагнитофон определенной модели цену, дифференцированную по регионам. Следующие данные показывают цены на видеомагнитофон в 8 различных регионах и соответствующее им число продаж:
| Число продаж, шт. | 420 | 380 | 350 | 400 | 440 | 380 | 450 | 420 |
| Цена, у.е. | 5,5 | 6,0 | 6,5 | 6,0 | 5,0 | 5,6 | 4,5 | 5,0 |
Решение
- Построим поле корреляции:
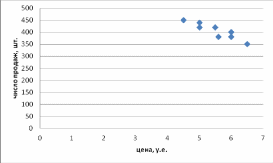
Очевидно, что число продаж видеомагнитофонов находится в обратной зависимости от установленных цен. Можно предположить, что зависимость линейная, так как расположение точек на графике по форме близко к прямой линии.
- Находим коэффициенты постулируемого уравнения регрессии, а также коэффициенты корреляции и детерминации. Для этого можно воспользоваться следующими формулами: yˆ x a bx
b xy x* y

a y bx
Приведём расчётную таблицу:
| № | у | х | у2 | х2 | ху | yˆ x | ( y уˆх )2 | ( y у)2 |
| 1 | 420 | 5,5 | 176400 | 30,25 | 2310 | 405,59 | 207,59 | 225 |
| 2 | 380 | 6 | 144400 | 36 | 2280 | 381,91 | 3,65 | 625 |
| 3 | 350 | 6,5 | 122500 | 42,25 | 2275 | 358,23 | 67,74 | 3025 |
| 4 | 400 | 6 | 160000 | 36 | 2400 | 381,91 | 327,21 | 25 |
| 5 | 440 | 5 | 193600 | 25 | 2200 | 429,27 | 115,07 | 1225 |
| 6 | 380 | 5,6 | 144400 | 31,36 | 2128 | 400,86 | 434,97 | 625 |
| 7 | 450 | 4,5 | 202500 | 20,25 | 2025 | 452,95 | 8,73 | 2025 |
| 8 | 420 | 5 | 176400 | 25 | 2100 | 429,27 | 85,99 | 225 |
| Сумма | 3240 | 44,1 | 1320200 | 246,11 | 17718 | 3240 | 1250,93 | 8000 |
| Среднее | 405 | 5,51 | 165025 | 30,76 | 2214,75 | 405 | 156,37 | 1000 |
Определим ряд характеристик моделируемых рядов:
х
у
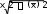


0,61
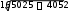
х
∑(х х)2 2 * n 0,612 * 8 3
Рассчитаем коэффициенты регрессии:
b 2214,74 5,51* 405 47,36 30,76 5,512
a 405 47,36 * 5,51 666,08
Таким образом, регрессионное уравнение имеет следующий вид:
yˆx 666,08 47,36x
Можно сделать вывод, что при росте цены на 1 у.е. число продаж видеомагнитофонов сокращается в среднем на 47,36 ≈ 47 шт. Условный объём продаж при нулевой цене равен 666 шт.
- Построим теоретическую линию регрессии:
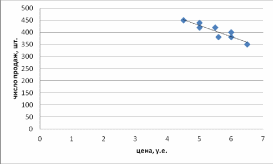
Так как эмпирические точки находятся вблизи теоретической прямой, то уравнение регрессии хорошо аппроксимирует данные.
- Определим линейный коэффициент корреляции:
r xy x* y 2214,74 5,51* 405 0,919
Коэффициент корреляции указывает на наличие связи и находится в интервале [-1;1]. В данном случае его отрицательное значение говорит об обратной связи между ценой видеомагнитофона и объёмом продаж. Связь весьма высокая по тесноте, так как |r| > 0,9.
Рассчитаем коэффициент детерминации:
R2 1
∑( y yˆх ) 2

1
1250,93
8000
0,844
Коэффициент детерминации показывает, что 84,4% вариации числа продаж видеомагнитофонов объясняется вариацией их цен, а остальные 15,6% — вариацией прочих факторов.
На основании данных расчётной таблицы рассчитаем остаточное среднее квадратическое отклонение:
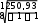
Определим стандартную ошибку для коэффициента регрессии:
mb S
ост *
14,44 *
8,32

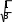
t b 47,36 5,69
m
b
b8,32
Табличное значение t-критерия Стьюдента при α = 0,05 и k = 8 – 1 – 1 = 6 будет равно tтабл
= 2,45. Таким образом, коэффициент регрессии оказался значим, так как расчётное значение t-критерия по модулю выше табличного значения.
Для определения значимости полученного уравнения регрессии необходимо рассчитать эмпирическую величину F-критерия Фишера:
R2
Fp 1 R2 *
n p 1
p
0,844 *
1 0,844
8 1 1
1
32,37
По таблице F-распределения Снедекора-Фишера при α = 0,05 и К1 = 1, К2 = 8 – 2 = 6 величина Fт = 5,99. Это означает, что гипотеза Н0 о несущественности связи между y и x с вероятностью ошибочности суждения α = 0,05 отклоняется, то есть связь между этими переменными может быть признана существенной.
- Спрогнозируем число продаж видеомагнитофонов при цене 5,75 у.е. за 1 шт.
yˆxр
666,08 47,36 * 5,75 393,75
Построим доверительные интервалы для индивидуальной прогнозной величины точке х* по следующим формулам:
yˆxр dy yˆxр yˆxр dy, где
yˆ xр в

, где
h 1
n
(x* x)2

1
8
(5,75 5,51) 2
3
0,14
Тогда:
dy 2,45 *14,44 *
393,75 37,79 yˆxр 393,75 37,79
355,97 yˆxр 431,54
Следовательно, с 95% уверенностью можно утверждать, что число продаж видеомагнитофонов компанией при цене 5,75 у.е. за 1 шт., находится в пределах от 356 до 431 шт.
Если нужно сделать вывод относительно числа продаж во всех компаниях со средней ценой видеомагнитофона 5,75 у.е., то необходимо построить доверительный интервал для
генерального среднего значения
ˆyген.
при заданном х*. Вариация в этом случае будет
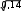
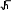
2,45 *14,44 *
13,4
393,75 13,4 yˆген 393,75 13,4
380,36 yˆген 407,15
Таким образом, с 95% уверенностью можно утверждать, что число продаж видеомагнитофонов во всех компаниях по средней цене 5,75 у.е. находится в пределах от 380 до 407 шт.
- Коэффициент эластичности определим по формуле:

yx y
0,61
31,62
0,64%
Итак, в относительном выражении при увеличении цены видеомагнитофона на 1%
возможно сокращение продаж в анализируемой компании на 0,64%.
2015-08-162015-08-16СтудИзба
Описание файла
Документ из архива «Математическая статистика (DOC)»,
который расположен в категории «».
Всё это находится в предмете «теория вероятностей и математическая статистика» из 7 семестр, которые можно найти в файловом архиве НИУ «МЭИ» .
Не смотря на прямую связь этого архива с НИУ «МЭИ» , его также можно найти и в других разделах. Архив можно найти в разделе «книги и методические указания», в предмете «теория вероятности и математическая статистика» в общих файлах.
Онлайн просмотр документа «Математическая статистика (DOC)»
Текст 6 страницы из документа «Математическая статистика (DOC)»
4) Компания, занимающаяся продажей радиоаппаратуры, установила на видеомагнитофон определённой модели цену, диффириенцированную по регионам. Следующие данные показывают цену в 8 различных регионах и соответствующее им число продаж.
|
Число продаж, шт. |
420 |
380 |
350 |
400 |
440 |
380 |
450 |
420 |
|
Цена, тыс. руб. |
5,5 |
6 |
6,5 |
6 |
5 |
6,5 |
4,5 |
5 |
Постройте график исходных данных и определите по нему характер зависимости. Рассчитайте выборочный коэффициент линейной корреляции Пирсона, проверьте его значимость при α = 0,01. Постройте уравнение регрессии и объясните смысл полученных результатов.
5) Опрос 10 студентов НХК позволяет выявить зависимость между средним баллом по результатам предыдущей сессии и числом часов в неделю затраченных студентом на самостоятельную подготовку.
|
Средний балл |
4,6 |
4,3 |
3,8 |
3,8 |
4,2 |
4,3 |
3,8 |
4 |
3,1 |
3,9 |
|
Число часов |
25 |
22 |
9 |
15 |
15 |
30 |
20 |
30 |
10 |
17 |
Постройте график исходных данных и определите по нему характер зависимости. Рассчитайте выборочный коэффициент линейной корреляции Пирсона, проверьте его значимость при α = 0,05. Постройте уравнение регрессии и дайте интерпретацию полученных результатов. Если студент занимается самостоятельно по 12 часов в неделю, то каков прогноз успеваемости?
6) Имеется случайная выборка из 10 семей для изучения связи между числом телевизоров (Y) в домохозяйстве и числом членов семьи (Х)
|
Х |
6 |
2 |
4 |
3 |
4 |
4 |
6 |
3 |
2 |
2 |
|
Y |
4 |
1 |
3 |
2 |
2 |
3 |
4 |
1 |
2 |
2 |
Постройте график исходных данных и определите по нему характер зависимости. Рассчитайте выборочный коэффициент линейной корреляции Пирсона, проверьте его значимость при α = 0,01. Постройте уравнение регрессии и дайте интерпретацию полученных результатов.
7) Имеются данные о стаже работы (Х, лет) и выработке одного рабочего за смену (Y, шт.)
|
Х |
1 |
3 |
4 |
5 |
6 |
7 |
|
Y |
14 |
15 |
18 |
20 |
22 |
25 |
Постройте график исходных данных и определите по нему характер зависимости. Рассчитайте выборочный коэффициент линейной корреляции Пирсона, проверьте его значимость при α = 0,05. Постройте уравнение регрессии и дайте интерпретацию полученных результатов.

|
Х |
2 |
3 |
4 |
5 |
6 |
|
Y |
1,9 |
1,7 |
1,8 |
1,6 |
1,4 |
Полагая, что между Х и Y имеет место линейная зависимость, определите выборочное уравнение линейной регрессии и объясните смысл полученных коэффициентов.
9) Имеются выборочные данные о глубине вспашки полей под озимые культуры (Х, см.) и их урожайность (Y, га)
|
Х |
10 |
15 |
20 |
25 |
30 |
|
Y |
5 |
10 |
16 |
20 |
24 |
При α = 0,05 установить значимость статистической связи между признаками Х и Y. Если признаки коррелируют, постройте уравнение регрессии и объясните его смысл. Сделайте прогноз урожайности пшеницы при глубине вспашки 22 см.
10) Из студентов 3-го курса групп ЭВМ отобраны случайным образом 10 человек и подсчитаны средние оценки, полученные ими на 1-ом (Х) и 3-м (Y) курсе.
|
Х |
3,5 |
4 |
3,8 |
4,6 |
3,9 |
3 |
3,5 |
3,9 |
4,5 |
4,1 |
|
Y |
4,2 |
3,9 |
3,8 |
4,5 |
4,2 |
3,4 |
3,8 |
3,9 |
4,6 |
3 |
Полагая, что между Х и Y имеет место линейная зависимость, определите выборочное уравнение линейной регрессии и объясните смысл полученных коэффициентов. Каковы значимость коэффициента корреляции, направление и теснота связи между показателями Х и Y, если α = 0,05?
11) Определите тесноту связи общего веса некоторого растения (Х, гр) и веса его семян (Y, гр) на основе следующих выборочных данных:
|
Х |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
|
Y |
20 |
25 |
28 |
30 |
35 |
40 |
45 |
Проверьте значимость выборочного коэффициента корреляции при α = 0,05. Постройте линейное уравнение регрессии и объясните его.
12) Перед сдачей экзаменов в конце семестра в 20 группах студентов НХК был проведён опрос о том, какую оценку по сдаваемым в сессию курсам они ожидают получить. После сессии средние полученные оценки были сопоставлены со средними ожидаемыми.
Результаты приведены в таблице:
|
Ожидаемая |
3,4 |
3,1 |
3 |
2,8 |
3,7 |
3,5 |
2,9 |
3,7 |
3,5 |
3,2 |
|
Полученная |
4,1 |
3,4 |
3,3 |
3 |
4,7 |
4,6 |
3 |
4,6 |
4,6 |
3,6 |
|
Ожидаемая |
3 |
3,5 |
3,3 |
3,1 |
3,3 |
3,9 |
2,9 |
3,2 |
3,4 |
3,4 |
|
Полученная |
3,5 |
4 |
3,6 |
3,1 |
3,3 |
4,5 |
2,8 |
3,7 |
3,8 |
3,9 |
Рассчитайте линейный коэффициент корреляции Пирсона, оцените его значимость при α = 0,05.
13) Определите тесноту связи между возрастом самолёта (Х, лет) и стоимостью его эксплуатации (Y, млн. руб.) по следующим данным:
|
Х |
1 |
2 |
3 |
4 |
5 |
|
Y |
2 |
4 |
5 |
8 |
10 |
Установите значимость коэффициента корреляции. Если он значим, то постройте уравнение регрессии и объясните его смысл. Каким будет прогноз стоимости эксплуатации самолёта, если его возраст 1,5 года, а уровень значимости принять равным 0,05?
14) Определите тесноту связи объёма выпуска продукции (Х, тыс. шт.) и себестоимости единицы изделия (Y, тыс. руб.) на основе следующих данных:
|
Х |
3 |
4 |
5 |
6 |
7 |
|
Y |
10 |
8 |
7 |
5 |
2 |
Проверьте значимость выборочного коэффициента корреляции на уровне значимости равном 0,05. Постройте уравнение линейной регрессии и объясните его.
15)Имеются данные по 14 предприятиям о производительности труда (Y, шт.) и коэффициенте механизации работ (Х, %).
|
Х |
32 |
30 |
36 |
40 |
41 |
47 |
56 |
54 |
60 |
55 |
61 |
67 |
69 |
76 |
|
Y |
20 |
24 |
28 |
30 |
31 |
33 |
34 |
37 |
38 |
40 |
41 |
43 |
45 |
48 |
Проверьте значимость выборочного коэффициента корреляции при α = 0,05. Постройте уравнение регрессии и объясните его.
Свежие статьи
Популярно сейчас
Зачем заказывать выполнение своего задания, если оно уже было выполнено много много раз? Его можно просто купить или даже скачать бесплатно на СтудИзбе. Найдите нужный учебный материал у нас!
Ответы на популярные вопросы
То есть уже всё готово?
Да! Наши авторы собирают и выкладывают те работы, которые сдаются в Вашем учебном заведении ежегодно и уже проверены преподавателями.
А я могу что-то выложить?
Да! У нас любой человек может выложить любую учебную работу и зарабатывать на её продажах! Но каждый учебный материал публикуется только после тщательной проверки администрацией.
А если в купленном файле ошибка?
Вернём деньги! А если быть более точными, то автору даётся немного времени на исправление, а если не исправит или выйдет время, то вернём деньги в полном объёме!
Отзывы студентов
Добавляйте материалы
и зарабатывайте!
Продажи идут автоматически
643
Средний доход
с одного платного файла
Обучение Подробнее
Примеры решений задач по эконометрике
В этом разделе вы найдете несколько готовые задачи с решениями по разным разделам эконометрики для студентов ВУЗов. Все примеры выложены бесплатно, вы можете их просмотреть, распечатать, изучить.
Если вам нужна помощь в выполнении ваших работ по эконометрике, обращайтесь: эконометрика на заказ. Делаем контрольные работы, лабораторные, выполняем решение задач в Эксель и специальных программах.
Задачи по эконометрике с решениями
Задача 1. По группе предприятий, производящих однородную продукцию, известно, как зависит себестоимость единицы продукции $y$ от факторов, приведенных в таблице. Определите с помощью коэффициентов эластичности силу влияния каждого фактора на результат. Проранжируйте факторы по силе влияния, сделайте вывод. Данные представлены в таблице.
Задача 2. В таблице указаны парные коэффициенты корреляции. Проведите анализ целесообразности включения заданных факторов в уравнение множественной линейной регрессии.
Задача 3. По некоторым территориям районов края известны значения средней суточного душевого дохода в у.е. (фактор $X$) и процент от общего дохода, расходуемого на покупку продовольственных товаров (фактор $Y$), таблица 1. Требуется для характеристики зависимости $Y$ от $X$ рассчитать параметры линейной, степенной, показательной функции и выбрать оптимальную модель (провести оценку моделей через среднюю ошибку аппроксимации $(А)$ и $F$-критерий Фишера.
Задача 4. На основе данных о доходах $Y$, расходах на промышленные товары $X_2$, наличии детей (табл. 1), необходимо построить модель с фиктивной переменной $D$ (принять $D = 1$, если дети есть; $D = 0$ при их отсутствии), вида: $$Y=b_0+ b_2 X_2+b D.$$ Проверить статистическую значимость коэффициентов. Сделать выводы.
Задача 5. Постройте линии регрессии $Y$ на $х$ и $Х$ на $у$ для двумерной с.в. $(X,Y)$, закон распределения которой задан таблицей, рассчитайте коэффициенты корреляции и детерминации.
Задача 6. 1) Постройте поле корреляции результативного и факторного признаков.
2) Определите параметры уравнения парной линейной регрессии. Дайте интерпретацию найденных параметров и всего уравнения в целом.
3) Постройте теоретическую линию регрессии, совместив ее с полем корреляции. Сделайте выводы.
4) Рассчитайте линейный коэффициент корреляции и поясните его смысл. Определите коэффициент детерминации и дайте его интерпретацию.
5) С вероятностью 0,95 оцените статистическую значимость коэффициента регрессии и уравнения регрессии в целом. Сделайте выводы.
6) С вероятностью 0,95 постройте доверительный интервал для прогноза оценки $y_t$ и доверительный интервал генерального значения.
7) Определите значение коэффициента эластичности и объясните его.
Компания, занимающаяся продажей радиоаппаратуры, установила на видеомагнитофон определенной модели цену, дифференцированную по регионам. Следующие данные показывают цены на видеомагнитофон в 8 различных регионах и соответствующее им число продаж.
Задача 7. В таблице приведены данные о прибыли $Y$ (в тыс. руб.) в зависимости от доли товара $А$ в грузообороте $X$ (%).
1. Построить корреляционное поле. Выдвинуть предположение о характере статистической зависимости между переменными $X$ и $Y$.
2. Найти параметры линейного уравнения регрессии. Поясните экономический смысл выборочного коэффициента регрессии.
3. Найти коэффициент парной корреляции и оценить тесноту связи на основе таблицы Чеддока.
4. Найти коэффициент детерминации $R^2$.
5. Оценить статистическую значимость уравнения регрессии на уровне 0,05, используя $F$-статистику.
6. Полученное уравнение регрессии изобразить графически. Сделать вывод о качестве построенной модели.
7. Вычислить прогнозное значение при прогнозном значении $x_0$, составляющем 130% от среднего уровня $x$.
Задача 8. По группе 18 заводов, производящих однородную продукцию, получено уравнение регрессии себестоимости продукции $Y$ (тыс. руб.) от уровня технической оснащенности $X$ (тыс. руб.): $$y_i = 20+700/x$$ Доля остаточной дисперсии в общей составила 0,19. Найдите индекс корреляции, а также проверьте статистическую значимость уравнения регрессии в целом с помощью критерия Фишера ($alpha = 0,05$).
Задача 9. По 25 предприятиям региона изучается зависимость выработки продукции на одного работника $у$ (тыс. руб.) от ввода в действие новых основных фондов $х_1$ (% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих $х_2$ (%). $$y_i=-1.725+0.903 x_1+0.081 x_2, , overline=9.6 , overline=6.27 , overline=22.3$$ Определить с помощью коэффициентов эластичности силу влияния каждого фактора на результат. Ранжировать факторы по силе влияния. Найти скорректированный коэффициент детерминации, если множественный коэффициент детерминации равен 0,74.
Задача 10. В результате исследования зависимости среднедневной заработной платы $Y$ от среднедушевого прожиточного минимуме в день одного трудоспособного $Х$ по $n$ территориям региона было получено линейное уравнение регрессии $y=bx+a$. Исследуйте остатки данного уравнения регрессии на гетероскедастичность с помощью теста Голдфельда-Квандта на уровне значимости $alpha = 0.01$, если остаточные суммы квадратов для первой и второй групп соответственно равны $S_1 = 0,07$ и $S_2 = 0,92$; число степеней свободы остаточных сумм квадратов равны $k=k_1=k_2=6$.
Задача 11. Применив необходимое и достаточное условие идентификации, определите, идентифицировано ли каждое из уравнений модели.
Решение задач по эконометрике
Эконометрика — это быстро развивающаяся отрасль науки, характеризующаяся математическим описанием рядов экономических данных и представлением таких данных в геометрической или графической форме.
Термин «эконометрика» был впервые использован в 1910 году. Эконометрика означает измерение экономики. Предпосылкой для возникновения эконометрики послужила давняя необходимость получить достаточное представление о количественных взаимосвязях в современной экономической жизни, которое не могли дать статистика, экономическая теория и математика по отдельности. Это подчеркивает междисциплинарный характер предмета. Кроме того, предпосылками возникновения эконометрики являются развитие количественных методов в экономических исследованиях, накопление бухгалтерских и статистических данных, а также создание современной микро- и макроэкономики. Современная экономика определяет эконометрику как «науку о моделировании экономических явлений для объяснения и прогнозирования их развития, а также для выявления и измерения их детерминант». Таким образом, эконометрика — это наука об измерении и анализе экономических явлений и экономических отношений с помощью математических и статистических методов.
 Ответы на вопросы по заказу заданий по эконометрике:
Ответы на вопросы по заказу заданий по эконометрике:

- Цена зависит от объёма, сложности и срочности. Присылайте любые задания по любым предметам — я изучу и оценю.

- Мне и моей команде под силу выполнить как срочный заказ, так и сложный заказ. Стандартный срок выполнения – от 1 до 3 дней. Мы всегда стараемся выполнять любые работы и задания раньше срока.

- Доработка бесплатна. Срок выполнения от 1 до 2 дней.

- Оценка стоимости бесплатна.

- Можно оплатить любым способом: картой Visa / MasterCard, с баланса мобильного, google pay, apple pay, qiwi и т.д.

- Если работу не зачли, и мы не смогли её исправить – верну полную стоимость заказа.

- Присылайте в любое время! Я стараюсь быть всегда онлайн.
Содержание:
Парная регрессия и корреляция
Задача 1
По территориям региона приводятся данные за 199Х г. (табл. 1.6). Таблица 1.6
1. Построить линейное уравнение парной регрессии
2. Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации.
3. Оценить статистическую значимость параметров регрессии и корреляции.
4. Выполнить прогноз заработной платы 

5. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.
Решение:
I. Для расчета параметров уравнения линейной регрессии строим расчетную таблицу (табл. 1.7). Таблица !.7
Получено уравнение регрессии:
С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
2. Тесноту линейной связи оценит коэффициент корреляции:
Это означает, что 52% вариации заработной платы 

Качество построенной модели оценивается как хорошее, так как 
3. Оценку статистической значимости параметров регрессии проведем с помощью 
Выдвигаем гипотезу 


Определим случайные ошибки
Фактические значения 
поэтому гипотеза 

Рассчитаем доверительный интервал для 
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью 

4. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит: 
прогнозное значение прожиточного минимума составит:
5. Ошибка прогноза составит:
Предельная ошибка прогноза, которая в 95% случаев не будет превышена, составит:
Доверительный интервал прогноза:
Выполненный прогноз среднемесячной заработной платы оказался надежным 

Возможно, вас также заинтересует эта ссылка:
Задача 2
По группе предприятий, производящих однородную продукцию, известно, как зависит себестоимость единицы продукции у от факторов, приведенных в табл. 1.8. Таблица 1.8
1. Определить с помощью коэффициентов эластичности силу влияния каждого фактора на результат.
2. Ранжировать факторы по силе влияния.
Решение:
1. Для уравнения равносторонней гиперболы
Для уравнения прямой
Для уравнения степенной зависимости
Для уравнения показательной зависимости
2. Сравнивая значения 

Для формирования уровня себестоимости продукции группы предприятий первоочередное значение имеют цены на энергоносители; в гораздо меньшей степени влияют трудоемкость продукции и отчисляемая часть прибыли. Фактором снижения себестоимости выступает размер производства: с ростом его на 1% себестоимость единицы продукции снижается на -0,97%.
Возможно, вас также заинтересует эта ссылка:
Задача 3
Зависимость потребления продукта 
уравнение регрессии
индекс корреляции
остаточная дисперсия
Провести дисперсионный анализ полученных результатов.
Решение:
Результаты дисперсионного анализа приведены в табл. 1.9. Таблица 1.9
В силу того что 

Реализация типовых задач на компьютере
Решение с помощью ППП Excel
1. Встроенная статистическая функция ЛИНЕЙН определяет параметры линейной репрессии 
1) введите исходные данные или откройте существующий файл, содержащий анализируемые данные;
2) выделите область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики или область 1×2 — для получения только оценок коэффициентов регрессии;
3) активизируйте Мастер функций любым из способов:
а) в главном меню выберите Вставка/Функция;
б) на панели инструментов Стандартная щелкните по кнопке Вставка функции;
4) в окне Категория (рис. 1.1) выберите Статистические, в окне Функция — ЛИНЕЙН. Щелкните по кнопке ОК;
5) заполните аргументы функции (рис. 1.2):
Известные значения 
Известные значения 
Константа — логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа — 0, то свободный член равен 0; Статистика — логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация
выводится, если Статистика 23 0, то выводятся только оценки параметров уравнения. Щелкните по кнопке ОК;
6) в левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу , а затем — на комбинацию клавиш + + .
Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
Для вычисления параметров экспоненциальной кривой

Для данных из примера 2 результат вычисления функции ЛИНЕИН представлен на рис. 1.3, функции ЛГРФПРИБЛ — на рис. 1.4.
2. С помощью инструмента анализа данных Регрессия, помимо результатов регрессионной статистики, дисперсионного анализа и доверительных интервалов, можно получить остатки и графики подбора линии регрессии, остатков и нормальной вероятности. Порядок действий следующий:
1) проверьте доступ к пакету анализа. В главном меню последовательно выберите Сервис /Надстройки. Установите флажок Пакет анализа (рис. 1.5);
2) в главном меню выберите Сервис/Анализ данных/Регрессия. Щелкните по кнопке ОК;
3) заполните диалоговое окно ввода данных и параметров вывода (рис. 1.6):
Входной интервал 
Входной интервал 
Метки — флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа — ноль — флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал — достаточно указать левую верхнюю ячейку будущего диапазона;
Новый рабочий лист — можно задать произвольное имя нового листа.
Если необходимо получить информацию и графики остатков, установите соответствующие флажки в диалоговом окне. Щелкните по кнопке ОК.
Результаты регрессионного анализа для данных из примера 2 представлены на рис. 1.7.
Возможно, вас также заинтересует эта ссылка:
Множественная регрессия и корреляция
Задача 4
По 20 территориям России изучаются следующие данные (табл. 2.2): зависимость среднегодового душевого дохода 


1. Составить таблицу дисперсионного анализа для проверки при уровне значимости 
2. С помощью частных 



3. Оценить с помощью 

Решение:
1. Задача дисперсионного анализа состоит в проверке нулевой гипотезы 
Анализ выполняется при сравнении фактического и табличного (критического) значений 






Результаты дисперсионного анализа представлены в табл. 2.3. Таблица 2.3
Сравнивая 

уравнения регрессии в целом и значения 
2. Частный 





Включение фактора 


Аналогично проверим целесообразность включения в модель дополнительного фактора 

В силу того что 



3. Оценка с помощью 




Табличные (критические) значения 




В нашем примере при 


коэффициент регрессии 





Возможно, вас также заинтересует эта ссылка:
Задача 5
Зависимость спроса на свинину 



1. Представить данное уравнение в естественной форме (не в логарифмах).
2. Оценить значимость параметров данного уравнения, если известно, что 



Решение:
1. Представленное степенное уравнение множественной регрессии приводим к естественной форме путём потенцирования обеих частей уравнения:
Значения коэффициентов регрессии 
Спрос на свинину 
2. Табличное значение 



которые свидетельствуют о случайной природе взаимосвязи, о статистической ненадежности всего уравнения, поэтому применять полученное уравнение для прогноза не рекомендуется.
Возможно, вас также заинтересует эта ссылка:
Задача 6
По 20 предприятиям региона (табл. 2.5) изучается зависимость выработки продукции на одного работника 


1. Оценить показатели вариации каждого признака и сделать вывод о возможностях применения МНК для их изучения.
2. Проанализировать линейные коэффициенты парной и частной корреляции.
3. Написать уравнение множественной регрессии, оценить значимость его параметров, пояснить их экономический смысл.
4. С помощью 

5. С помощью частных 



6. Рассчитать средние частные коэффициенты эластичности и дать на их основе сравнительную оценку силы влияния факторов на результат.
Реализация типовых задач на компьютере
1. Решение примера проведем с использованием ППП MS Excel и Statgraphics.
Решение с помощью ППП Excel
Сводную таблицу основных статистических характеристик для одного или нескольких массивов данных можно получить с помощью инструмента анализа данных Описательная статистика. Для этого выполните следующие шаги:
1) введите исходные данные или откройте существующий файл, содержащий анализируемые данные;
2) в главном меню выберите последовательно пункты Сервис / Анализ данных / Описательная статистика, после чего щелкните по кнопке ОК;
3) заполните диалоговое окно ввода данных и параметров вывода (рис. 2.1);
Входной интервал — диапазон, содержащий анализируемые данные, это может быть одна или несколько строк (столбцов); Группирование — по столбцам или по строкам — необходимо указать дополнительно;
Метки — флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Выходной интервал — достаточно указать левую верхнюю ячейку будущего диапазона;
Новый рабочий лист — можно задать произвольное имя нового листа.
Если необходимо получить дополнительную информацию Итоговой статистики, Уровня надежности, 
Результаты вычисления соответствующих показателей для каждого признака представлены на рис. 2.2.
Решение с помощью ППП Statgraphics
Для проведения многофакторного анализа в ППП Statgraphics используется пункт меню Multiple Variable Analysis. Для получения показателей описательной статистики необходимо проделать следующие операции:
1) ввести исходные данные или открыть существующий файл, содержащий анализируемые данные;
2) в главном меню выбрать Describe/Numeric Data/Multiple Variable Analysis;
3) заполнить диалоговое окно ввода данных (рис. 2.3). Ввести названия всех столбцов, значения которых вы хотите включить в анализ; щелкнуть по кнопке ОК;
4) в окне табличных настроек поставить флажок напротив Summary Statistics (рис. 2.4). Итоговая статистика — показатели вариации -появится в отдельном окне.



Совокупность предприятий однородна, и для ее изучения могут использоваться метод наименьших квадратов и вероятностные методы оценки статистических гипотез.
2. Значения линейных коэффициентов парной корреляции определяют тесноту попарно связанных переменных, использованных в данном уравнении множественной регрессии. Линейные коэффициенты частной корреляции оценивают тесноту связи значений двух переменных, исключая влияние всех других переменных, представленных в уравнении множественной регрессии.
Решение с помощью ППП Excel
К сожалению, в ППП MS Excel нет специального инструмента для расчета линейных коэффициентов частной корреляции. Матрицу парных коэффициентов корреляции переменных можно рассчитать, используя инструмент анализа данных Корреляция. Для этого:
1) в главном меню последовательно выберите пункты Сервис / Анализ данных / Корреляция. Щелкните по кнопке ОК;
2) заполните диалоговое окно ввода данных и параметров вывода (см. рис. 2.1);
3) результаты вычислений — матрица коэффициентов парной корреляции — представлены на рис. 2.6.
Решение с помощью ППП Statgraphics
При проведении многофакторного анализа — Multiple Variable Analysis — вычисляются линейные коэффициенты парной корреляции и линейные коэффициенты частной корреляции. Последовательность операций описана в п.1 этого примера. Для отображения результатов вычисления на экране необходимо установить флажки напротив Correlations и Partial Correlations в окне табличных настроек (рис. 2.7).
В результате получим матрицы коэффициентов парной и частной корреляции (рис. 2.8).
Значения коэффициентов парной корреляции указывают на весьма тесную связь выработки 

Коэффициенты частной корреляции дают более точную характеристику тесноты связи двух признаков, чем коэффициенты парной корреляции, так как очишают парную зависимость от взаимодействия данной пары признаков с другими признаками, представленными в модели. Наиболее тесно связаны 







Если сравнить коэффициенты парной и часгной корреляции, то можно увидеть, что из-за высокой межфакторной зависимости коэффициенты парной корреляции дают завышенные оценки тесноты связи:
Именно по этой причине рекомендуется при наличии сильной коллинеарности (взаимосвязи) факторов исключать из исследования тот фактор, у которого теснота парной зависимости меньше, чем теснота межфакторной связи.
3. Вычисление параметров линейного уравнения множественной регрессии.
Система эконометрических уравнений
Задача 7
Изучается модель вида
где 




Информация за девять лет о приростах всех показателей дана в табл. 3.1
Таблица 3.1
Для данной модели была получена система приведенных уравнений:
1. Провести идентификацию модели.
2. Рассчитать параметры первого уравнения структурной модели.
Решение:
1. В данной модели две эндогенные переменные 

Первое уравнение сверхидентифицировано, так как в нем на параметры при 




2. Для определения параметров сверхидентифицированной модели используется двухшаговый метод наименьших квадратов.
Шаг 1. На основе системы приведенных уравнений по точно идентифицированному второму уравнению определим теоретические значения эндогенной переменной 
подставим значения 
Шаг 2. По сверхидентифицированному уравнению структурной формы модели заменяем фактические значения 


Далее к сверхидентифицированному уравнению применяется метод наименьших квадратов. Обозначим новую переменную 

Система нормальных уравнений составит:
Итак, первое уравнение структурной модели будет таким:
Задача 8
Имеются данные за 1990-1994 гг. (табл. 3.3). 4 Таблица 3.3
Требуется: Построить модель вида
рассчитав соответствующие структурные коэффициенты.
Решение:
Система одновременных уравнений с двумя эндогенными и двумя экзогенными переменными имеет вид
В каждом уравнении две эндогенные и одна отсутствующая экзогенная переменная из имеющихся в системе. Для каждого уравнения данной системы действует счетное правило 2=1 + 1. Это означает, что каждое уравнение и система в целом идентифицированы.
Для определения параметров такой системы применяется косвенный метод наименьших квадратов.
С этой целью структурная форма модели преобразуется в приведенную форму:
в которой коэффициенты при 
Для нахождения значений 
При ее решении предполагается, что 
Применительно к ней необходимые суммы оказываются следующими:
Система нормальных уравнений составит:
Решая ее, получим:
Итак, имеем
Аналогично строим систему нормальных уравнений для определения коэффициентов
тогда второе уравнение примет вид
Приведенная форма модели имеет вид
Из приведенной формы модели определяем коэффициенты структурной модели:
Итак, структурная форма модели имеет вид
Возможно, вас также заинтересует эта ссылка:
Задача 8
Имеются следующие данные о величине дохода на одного члена семьи и расхода на товар 
Таблица 4.3
1. Определить ежегодные абсолютные приросты доходов и расходов и сделать выводы о тенденции развития каждого ряда.
2. Перечислить основные пути устранения тенденции для построения модели спроса на товар 
3. Построить линейную модель спроса, используя первые разности уровней исходных динамических рядов.
4. Пояснить экономический смысл коэффициента регрессии.
5. Построить линейную модель спроса на товар 
Решение:
1. Обозначим расходы на товар 


Расчеты можно оформить в виде таблицы (табл. 4.4). Таблица 4.4
2. Так как ряды динамики имеют общую тенденцию к росту, то для построения регрессионной модели спроса на товар 

Другой возможный путь учета тенденции при построении моделей — найти по каждому ряду уравнение тренда:
и отклонения от него:
Далее модель строится по отклонениям от тренда:
При построении эконометрических моделей чаще используется другой путь учета тенденции — включение в модель фактора времени. Иными словами, модель строится по исходным данным, но в нее в качестве самостоятельного фактора включается время, т.е.
3. Модель имеет вид
Для определения параметров 
Применительно к нашим данным имеем
Решая эту систему, получим:
откуда модель имеет вид
4. Коэффициент регрессии 

5. Модель имеет вид
Применяя МНК, получим систему нормальных уравнений:
Расчеты оформим в виде табл. 4.5. Таблица 4.5
Система уравнений примет вид
Решая ее, получим
Уравнение регрессии имеет вид
Параметр 




Задача 9
По данным за 30 месяцев некоторого временного ряда 


1. Охарактеризовать структуру этого ряда, используя графическое изображение.
2. Для прогнозирования значений 
Решение:
1. Так как значения всех коэффициентов автокорреляции достаточно высокие, ряд содержит тенденцию. Поскольку наибольшее абсолютное значение имеет коэффициент автокорреляции 4-го порядка 
График этого ряда можно представить на рис. 4.1.

так как значение 
Кроме того, возможно построение и множественного уравнения авторегрессии 
Сравнить полученные уравнения и выбрать наилучшее решение можно с помощью скорректированного коэффициента детерминации.
Реализация типовых задач на компьютере
Решение с использованием ППП MS Excel
1. Для определения параметров линейного тренда по методу наименьших квадратов используется статистическая функция ЛИНЕЙН, для определения экспоненциального тренда -ЛГРФПРИБЛ. Порядок вычисления был рассмотрен в 1-м разделе практикума. В качестве зависимой переменной в данном примере
выступает время 
функций ЛИНЕЙН и ЛГРФПРИБЛ (рис. 4.2 и 4.3).
Запишем уравнения линейного и экспоненциального тренда, используя данные рис. 4.2 и 4.3:
2. Построение графиков осуществляется с помощью Мастера диаграмм.
Порядок построения следующий:
1) введите исходные данные или откройте существующий файл, содержащий анализируемые данные;
2) активизируйте Мастер диаграмм любым из следующих способов:
а) в главном меню выберите Вставка/Диаграмма;
б) на панели инструментов Стандартная щелкните по кнопке Мастер диаграмм;
3) в окне Тип выберите График (рис. 4.4); вид графика выберите в поле рядом со списком типов. Щелкните по кнопке Далее;
4) заполните диапазон данных, как показано на рис. 4.5. Установите флажок размещения данных в столбцах (строках). Щелкните по кнопке Далее;
5) заполните параметры диаграммы на разных закладках (рис. 4.6): названия диаграммы и осей, значения осей, линии сетки, параметры легенды, таблица и подписи данных. Щелкните по кнопке Далее;
6) Укажите место размещения диаграммы на отдельном или имеющимся листе(рис. 4.7) Щелкните по кнопке далее. Готовая диаграмма, отражающая динамику уровней изучаемого ряда, представлена на рис 4.8

1) выделите область построения диаграммы; в главном меню выберите Диаграмма/Добавить линию тренда;
2) в появившемся диалоговом окне (рис. 4.9) выберите вид линии тренда и задайте соответствующие параметры. Для полиномиального тренда необходимо задать степень аппроксимирующего полинома, для скользящего среднего — количество точек усреднения.
В качестве дополнительной информации на диаграмме можно отобразить уравнение регрессии и значение среднеквадратического отклонения, установив соответствующие флажки на закладке Параметры (рис. 4.10). Щелкните по кнопке ОК.
На рис 4.11-4.15 представлены различные виды трендов, описывающие исходные данные задачи
3. Сравним значения 
Исходные данные лучше всего описывает полином 6-й степени. Следовательно, в рассматриваемом примере для расчета прогнозных значений следует использовать полиномиальное уравнение.
Возможно, вас также заинтересует эта ссылка:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Примеры решений задач по эконометрике
Парная регрессия и корреляция
- Оценка параметров уравнения регрессии
- Пример нахождения коэффициента корреляции (линейный коэффициент корреляции Пирсона). Значимость коэффициента корреляции.
- Пример нахождения доверительных интервалов коэффициентов регрессии
- Пример нахождения коэффициента детерминации
- Пример нахождения статистической значимости коэффициентов регрессии (параметров регрессии)
- Средняя ошибка аппроксимации
По семи территориям Уральского района За 199Х г. известны значения двух признаков.
По территориям региона приводятся данные за 199Х г. - Парная нелинейная регрессия и корреляция
Изучается зависимость материалоемкости продукции от размера предприятия по 10 однородным заводам (см. таблицу). - Экспоненциальное уравнение регрессии
Парная нелинейная регрессия и корреляция
- Парная нелинейная регрессия и корреляция
Изучается зависимость материалоемкости продукции от размера предприятия по 10 однородным заводам (см. таблицу). - Экспоненциальное уравнение регрессии
- Индекс корреляции (для нелинейной связи)
- Другие примеры для нелинейной связи (Аналитическое выравнивание ряда по параболе, степенной функции)
Регрессионный и корреляционный анализа
- Пример регрессионного анализа
- Корреляционный анализ
- Поле корреляции и формулирование гипотезы о форме связи
По территории Северного, Северо-Западного и Центрального районов известны данные за ноябрь 1997 г. - Решение контрольной работы по эконометрике
По 12 предприятиям концерна изучается зависимость прибыли (тыс. руб.) Y от выработки продукции на одного человека (единицу) по следующим данным (см. таблицу) - Практикум по эконометрике
- Методические рекомендации по подготовке контрольных работ
Исследовать статистическую зависимость между парой показателей: Х < 10, 22, 15, 22, 7, 14, 20>и Y <5, 1, 3, 2, 7, 4, 1 > - Эконометрическое исследование
- Тест Голдфелда-Квандта
- Пример проверки наличия в модели автокорреляции
- Частные F-критерии
Непараметрические показатели связи
Эконометрические методы проведения экспертных исследований
Статистические таблицы
- Шкала Чеддока. Применяется для оценки показателей тесноты связи (коэффициента линейной корреляции, коэффициента Фехнера, коэффициента ранговой корреляции Спирмена).
- Статистические таблицы Стьюдента и Фишера. используются для оценки качества полученного уравнения регрессии.
- Статистические таблицы Дарбина-Уотсона. используется для анализа автокорреляции.
- Распределение ХИ квадрат (X 2 ). Используется для определения доверительного интервала дисперсии и проверке гипотез о виде распределения.
- Критические значения критерия U Манна-Уитни.
Эконометрический анализ в Excel
Оформление решений
Оформление отчета по форме №2
Поскольку 5.22 > 2.752, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Поскольку 3.56 > 2.752, то статистическая значимость коэффициента регрессии a подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Доверительный интервал для коэффициентов уравнения регрессии.
Для расчета доверительного интервала определяем предельную ошибку Δ для каждого показателя:
Δb = ±tтаблmb = ±2.752*0.441 = 1.213
Доверительный интервал: b — Δb ≤ b ≤ b + Δb
5.22 — 1.213 ≤ b ≤ 5.22 + 1.213
1.089 ≤ b ≤ 3.515
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
Δa = ±tтаблma = ±2.752*36.855 = 101.426
Доверительный интервал: a — Δa ≤ a ≤ a + Δa
3.56 — 101.426 ≤ a ≤ 3.56 + 101.426
-232.492 ≤ a ≤ -29.64
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
источники:
http://natalibrilenova.ru/reshenie-zadach-po-ekonometrike/
http://math.semestr.ru/corel/corel_practice.php
Компания, занимающаяся продажей радиоаппаратуры, установила на видеомагнитофон определенной модели цену, дифференцированную по регионам. Следующие данные показывают цены на видеомагнитофон в 8 различных регионах и соответствующее им число продаж:
Номер региона Число продаж, шт.,
y Цена, у.е,
x
1 410 5.5
2 370 6.1
3 350 6.5
4 400 6.2
5 440 5.0
6 380 5.7
7 440 4.5
8 410 5.0
1) Определите параметры уравнения парной линейной регрессии. Дайте интерпретацию найденных параметров и всего уравнения в целом.
2) Постройте теоретическую линию регрессии, совместив ее с полем корреляции. Сделайте выводы.
3) Рассчитайте линейный коэффициент корреляции и поясните его смысл. Определите коэффициент детерминации и дайте его интерпретацию.
4) С вероятностью 0,95 оцените статистическую значимость коэффициента регрессии и уравнения регрессии в целом. Сделайте выводы.
5) С вероятностью 0,95 постройте доверительный интервал для прогноза оценки yi и доверительный интервал генерального значения y при x* = 5,75.
6) Определите значение коэффициента эластичности и объясните его.
Проводится исследование зависимости числа продаж видеомагнитофонов (y) от цены (х) по статистическим данным выборки.
1)
Зависимая переменная y – число продаж, шт.
Фактор х – цена видеомагнитофона, у.е.
Диаграмма рассеивания:
По диаграмме можно сделать вывод, что между признаками наблюдается линейная убывающая связь.
Эта связь, то есть зависимость у от х описывается уравнением
у=b0+b1*x
Для оценки коэффициентов уравнения b0 и b1 применяют метод наименьших квадратов, он состоит в минимизации суммы квадратов отклонений фактических значений зависимой переменной yi от расчетных yi
yi-yi2=yi-(b0+b1xi)2b0,b1min
Чтобы решить задачу минимизации, то есть рассчитать b0 и b1, нужно составить и решить относительно b0 и b1 систему нормальных уравнений
nb0+b1∑xi = ∑yib0∑xi+b1∑xi2=∑xiyi
Решением системы являются
b1=∑xiyi-1n∙∑xi·∑yi∑xi2-1n∑xi2
b0=∑yin-b1∙∑xin
Расчеты проведены в Excel:
Уравнение регрессии
у=626,89-40,79*x
Коэффициент b1=-40,79 показывает, что при увеличении цены на видеомагнитофон (за 1 шт.) на 1 у.е
. количество проданных единиц (число продаж y) снижается на 40,79 шт. в среднем.
Коэффициент b0=626,89 интерпретировать можно так: если бы цена на видеомагнитофон (за 1 шт.) была равна 0 у.е., мы бы “продали” 626,89 штук в среднем (то есть отдали бы даром).
2)
Найдем прогнозные значения yi и построим теоретическую линию регрессии.
Можно сделать вывод о том, что модель адекватна исходным данным.
3)
Рассчитаем следующие суммы квадратов
Общая сумма квадратов (общая дисперсия)
Qобщ=yi-y2
Сумма квадратов остатков (остаточная дисперсия)
Qост=yi-yi2
Сумма квадратов, объясненная регрессией
Qрегр=yi-y2
Коэффициент детерминации показывает долю дисперсии зависимой переменной у, объясненную уравнением и является мерой адекватности построенной модели.
Формула расчета
R2=1-QостQобщ
R2=1-1611,917200=0,7761
77,61% дисперсии количества проданных единиц видеомагнитофонов объяснено построенной моделью. Так как процент высокий, модель адекватно описывает исходные данные.
Линейный коэффициент корреляции является мерой линейной зависимости между зависимой переменной у и фактором х.
Формула расчета
R=R2
R=0,7761=0,88
Так как R > 0,7 то связь между признаками сильная.
4)
Для оценки значимости уравнения регрессии рассчитаем F-статистику
Fнабл=Qрегр1Qост(n-2)=5588,091611,91/6=20,8
Критическое значение распределения Фишера при уровне значимости = 0,05 и числе степеней свободы k1 = 1 и k2 = n – 2 найдем функцией Excel FРАСПОБР с параметрами (0,05;1;8-2)
Fкрит=5,987
Так как Fнабл > Fкрит, то уравнение признается значимым с вероятностью 95%.
Статистическая значимость коэффициентов регрессии проверяется критерием Стьюдента.
Сначала вычисляются стандартизированные ошибки коэффициентов регрессии
Sb0=Qостn-2*x2n*x-x2
Sb1=Qостn-2*1(x-x)2
Далее t-статистики коэффициентов
tb0=b0Sb0
tb1=b1Sb1
Далее критическое значение распределения Стьюдента при уровне значимости = 0,05 и числе степеней свободы k = n – 2 функцией Excel
tкрит= СТЬЮДРАСПОБР(0,05; 8-2)
Расчеты с помощью Excel
Так как расчетные t-статистики по модулю больше чем критическое значение распределения Стьюдента:
tb0>tкрит
tb1>tкрит
то оба коэффициента b0 и b1 значимы с вероятностью 95%.
Интервальные оценки генеральных параметров β0 и β1
b0-tкрит*Sb0<β0<b0+tкрит*Sb0
b1-tкрит*Sb1<β1<b1+tкрит*Sb1
С доверительной вероятностью 95% параметры попадают в интервалы:
β0∈(504,34;749,44)
β1∈-62,67;-18,91
5)
По уравнению у=626,89-40,79*x
точечный прогноз зависимой переменной y (число проданных видеомагнитофонов, шт.) при цене x* = 5,75 у.е.
y*=626,89-40,79*5,75=392,35
Стандартная ошибка прогноза
Sy*=Qостn-2∙1+1n+(x*-x)2(x-x)2
Интервальный прогноз зависимой переменной Y
y*-tкрит*Sy*<Y*<y*+tкрит*Sy*
С доверительной вероятностью 95% число проданных видеомагнитофонов Y при цене 5,75 у.е

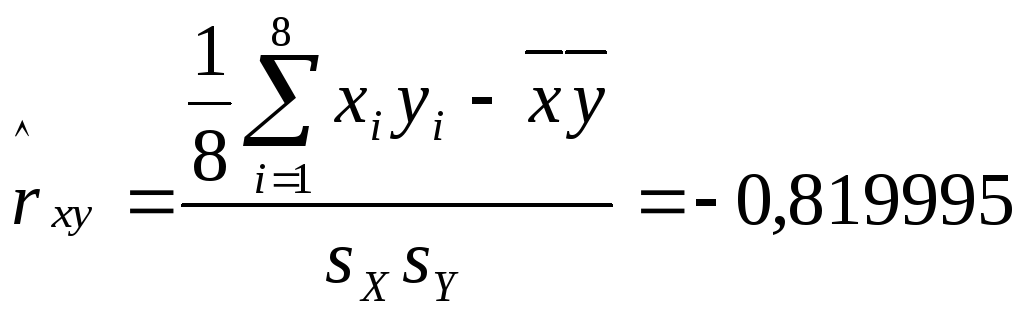

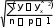

 Ответы на вопросы по заказу заданий по эконометрике:
Ответы на вопросы по заказу заданий по эконометрике:





























































































































