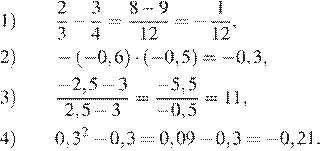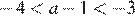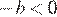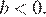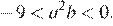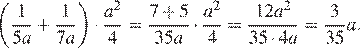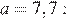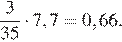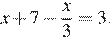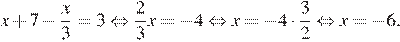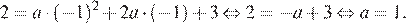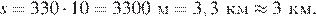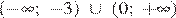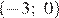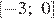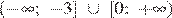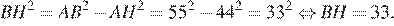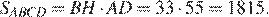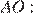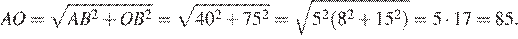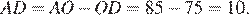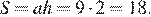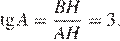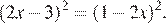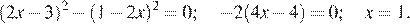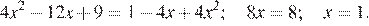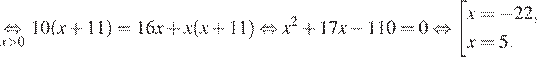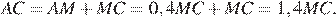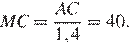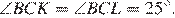Компания выбирает место для строительства торгово‐развлекательного комплекса: на месте квартала старых одноэтажных домов в центре города или на окраине города. Стоимость прокладки 1 метра коммуникаций равна 6000 рублей. В аренду планируется сдавать 4000 м2 площади комплекса. Стоимость земли, цена строительства комплекса с учётом сноса старых зданий и предполагаемая стоимость сдачи даны в таблице.
| Место | Цена земли (млн руб.) |
Цена строительства (млн руб.) |
Длина коммуникаций (м) |
Стоимость аренды за 1 м2 (руб./месяц) |
|---|---|---|---|---|
| Центр | 64,4 | 176 | 200 | 1200 |
| Окраина | 11,2 | 168 | 3500 | 900 |
Обдумав оба варианта, компания выбрала местом для строительства центр города. Через сколько месяцев после начала сдачи в аренду торговых площадей построенного комплекса более высокая стоимость аренды компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций? Ответ округлите до целых.
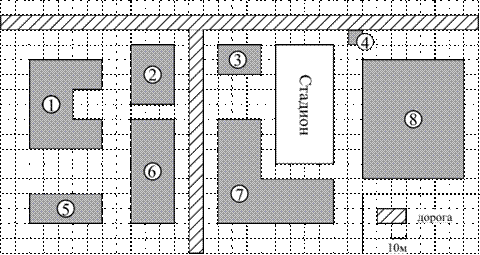
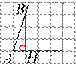
На плане (см. рис.) изображён район города, в котором живёт Петя. Сторона каждой клетки на плане равна 10 м.
Дом, в котором живёт Петя, обозначен цифрой 6. Прямо напротив дома, где живёт Петя, через дорогу находится дом в форме буквы «Г», где живёт его друг Вася. Рядом с домом, где живёт Петя, расположен дом, где живёт одноклассница Таня, а напротив него через дорогу имеется здание банка площадью 600 м2. А с другой стороны дома, где живёт Таня, расположен детский сад. Недалеко от детского сада и дома, где живёт Петя, находится магазин. Также имеется автобусная остановка, обозначенная цифрой 4, а в десяти метрах от неё — квартал старых одноэтажных домов.
1
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Банк | Магазин | Дом, где живёт Таня |
Квартал старых домов |
|---|---|---|---|---|
| Цифры |
Источник: Тренировочный вариант № 231, усложнённая версия, Александр Ларин
2
Территорию стадиона необходимо засеять газонной травой. В одной упаковке газонной травы содержится 12 кг семян, при этом для засеивания 3 м2 земли необходимо 100 г семян. Какое минимальное количество упаковок газонной травы необходимо приобрести?
Источник: Тренировочный вариант № 231, усложнённая версия, Александр Ларин
3
Найдите суммарную площадь, которую занимают дома, где проживают Таня, Петя и Вася. Ответ дайте в м2.
Источник: Тренировочный вариант № 231, усложнённая версия, Александр Ларин
4
Найдите расстояние от дома, где живёт Петя, до автобусной остановки (расстояние между двумя ближайшими точками по прямой) в метрах.
Источник: Тренировочный вариант № 231, усложнённая версия, Александр Ларин
Спрятать решение
Решение.
Стоимость постройки ТРК в центре города равна
рублей.
Стоимость постройки ТРК на окраине города равна
рублей.
Разница в стоимости составляет
рублей.
Разница в стоимости аренды составляет
рублей.
Значит, более высокая стоимость аренды компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций через месяцев. Округляя, получаем ответ — 35 месяцев.
Ответ: 35.
Источник: Тренировочный вариант № 231, усложнённая версия, Александр Ларин
6 декабря 2022 13:02
398
компания выбирает место для строительства торгово-развлекательного комплекса:на месте квартал старых одноэтажных домов в центре города или на окраине города.стоимость прокладки 1 метра коммуникации равна 6000 руб.в аренду планирует создавать 4000 кв.м.площади комплекса.стоимость земли цена строительства комплекса с учетом сноса старых зданий и предполагаемая стоимость сдачи в аренду в таблице.обдумав оба варианта компания выбрала место для строительства центр города.Через сколько месяцев после начала сдачи в аренду торговых площадей построенного комплекса более высокая стоимость аренды компенсирует разность в стоимости земли,строительство и прокладывания коммуникаций,если компания платит налог 13% стоимости,полученных за сдачу в аренду?Ответ округлите до целых.
Посмотреть ответы
1 млн = 1 000 000
1)
6 000 · 200 = 1 200 000 (руб.) — стоимость прокладки коммуникаций в центре;
1 200 000 руб. = 1,2 млн руб.;
64,4 + 176 + 1,2 = 241,6 (млн руб.) —
затраты на постройку ТРК в центре
.
2)
6 000 · 3 500 = 21 000 000 (руб.) — стоимость прокладки коммуникаций на окраине;
21 000 000 руб. = 21 млн руб.;
11,2 + 168 + 21 = 200,2 (млн руб.) —
затраты на постройку ТРК на окраине
.
3)
241,6 — 200,2 = 41,4 (млн руб.) —
разность в стоимости земли, строительства и прокладывания коммуникаций
.
4)
1 200 — 900 = 300 (руб./месяц) — разность в стоимости аренды за 1 м².
После уплаты налога в 13% аренда принесёт 100%-13%=87% от прибыли без налогов.
1% от чего-то составляет 0,01 долю от того же.
300 · 0,87 = 261 (руб./месяц) — разность в стоимости аренды за 1 м², с учётом уплаты налогов.
261 · 4 000 = 1 044 000 (руб./месяц) —
разность в стоимости аренды за 4 000 м², с учётом уплаты налогов
.
1 044 000 руб./месяц = 1,044 млн руб./месяц
5) (мес.) — время за которое компенсируется разность.
Ответ
: 40.
Еще вопросы по категории Математика
Тип 1 № 367690
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Банк | Магазин | Дом, где живёт Таня | Квартал старых домов |
|---|---|---|---|---|
| Цифры |
На плане (см. рис.) изображён район города, в котором живёт Петя. Сторона каждой клетки на плане равна 10 м.
Дом, в котором живёт Петя, обозначен цифрой 6. Прямо напротив дома, где живёт Петя, через дорогу находится дом в форме буквы «Г», где живёт его друг Вася. Рядом с домом, где живёт Петя, расположен дом, где живёт одноклассница Таня, а напротив него через дорогу имеется здание банка площадью 600 м2. А с другой стороны дома, где живёт Таня, расположен детский сад. Недалеко от детского сада и дома, где живёт Петя, находится магазин. Также имеется автобусная остановка, обозначенная цифрой 4, а в десяти метрах от неё — квартал старых одноэтажных домов.
2. Тип 2 № 367691
Территорию стадиона необходимо засеять газонной травой. В одной упаковке газонной травы содержится 12 кг семян, при этом для засеивания 3 м2 земли необходимо 100 г семян. Какое минимальное количество упаковок газонной травы необходимо приобрести?
3. Тип 3 № 367692
Найдите суммарную площадь, которую занимают дома, где проживают Таня, Петя и Вася. Ответ дайте в м2.
4. Тип 4 № 367693
Найдите расстояние от дома, где живёт Петя, до автобусной остановки (расстояние между двумя ближайшими точками по прямой) в метрах.
5. Тип 5 № 367694
Компания выбирает место для строительства торгово‐развлекательного комплекса: на месте квартала старых одноэтажных домов в центре города или на окраине города. Стоимость прокладки 1 метра коммуникаций равна 6000 рублей. В аренду планируется сдавать 4000 м2 площади комплекса. Стоимость земли, цена строительства комплекса с учётом сноса старых зданий и предполагаемая стоимость сдачи даны в таблице.
| Место | Цена земли (млн руб.) | Цена строительства (млн руб.) | Длина коммуникаций (м) | Стоимость аренды за 1 м2 (руб./месяц) |
|---|---|---|---|---|
| Центр | 64,4 | 176 | 200 | 1200 |
| Окраина | 11,2 | 168 | 3500 | 900 |
Обдумав оба варианта, компания выбрала местом для строительства центр города. Через сколько месяцев после начала сдачи в аренду торговых площадей построенного комплекса более высокая стоимость аренды компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций? Ответ округлите до целых.
6. Тип 6 № 337273
Найдите значение выражения
7. Тип 7 № 341320
На координатной прямой точками отмечены числа
Какому числу соответствует точка B?
1)
2)
3) 0,42
4) 0,45
8. Тип 8 № 338092
Найдите если
9. Тип 9 № 338503
Решите уравнение
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
10. Тип 10 № 311391
Какова вероятность того, что случайно выбранное натуральное число от 15 до 29 делится на 5?
11. Тип 11 № 351965
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А)
Б)
В)
ГРАФИКИ
В таблице под каждой буквой укажите соответствующий номер.
12. Тип 12 № 311528
Площадь треугольника можно вычислить по формуле
, где a — сторона треугольника, h — высота, проведенная к этой стороне (в метрах). Пользуясь этой формулой, найдите сторону
, если площадь треугольника равна
, а высота h равна 14 м.
13. Тип 13 № 320666
Укажите неравенство, решением которого является любое число.
В ответе укажите номер правильного варианта.
1) x2 − 15 < 0
2) x2 + 15 > 0
3) x2 + 15 < 0
4) x2 − 15 > 0
14. Тип 14 № 394399
Мать дарит каждой из пяти своих дочерей в день рождения, начиная с пяти лет, столько книг, сколько дочери лет. Возрасты пяти дочерей составляют арифметическую прогрессию, разность которой равна 2. Сколько лет было старшей дочери, когда у них составилась библиотека общей численностью в 495 книг?
15. Тип 15 № 311412
Углы, отмеченные на рисунке одной дугой, равны. Найдите угол α. Ответ дайте в градусах.
16. Тип 16 № 102
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
17. Тип 17 № 39
Найдите площадь трапеции, изображённой на рисунке.
18. Тип 18 № 348467
На клетчатой бумаге с размером клетки 1×1 изображен прямоугольный треугольник. Найдите длину его большего катета.
19. Тип 19 № 341525
Какие из следующих утверждений верны?
1) Треугольника со сторонами 1, 2, 4 не существует.
2) Сумма углов любого треугольника равна 360 градусам.
3) Серединные перпендикуляры к сторонам треугольника пересекаются в центре его описанной окружности.
Если утверждений несколько, запишите их номера в порядке возрастания.
20. Тип 20 № 311599
Какое из чисел больше: или
?
21. Тип 21 № 314431
При смешивании первого раствора кислоты, концентрация которого 20%, и второго раствора этой же кислоты, концентрация которого 50%, получили раствор, содержащий 30% кислоты. В каком отношении были взяты первый и второй растворы?
22. Тип 22 № 338207
Постройте график функции и определите, при каких значениях m прямая
имеет с графиком ровно две общие точки.
23. Тип 23 № 311666
Диагонали AC и BD трапеции ABCD пересекаются в точке O. Площади треугольников AOD и BOC равны соответственно и
. Найдите площадь трапеции.
24. Тип 24 № 311969
Окружность касается стороны AB треугольника ABC, у которого ∠C = 90°, и продолжений его сторон AC и BC за точки A и B соответственно. Докажите, что периметр треугольника ABC равен диаметру этой окружности.
25. Тип 25 № 333027
Две касающиеся внешним образом в точке K окружности, радиусы которых равны 16 и 48, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
Просмотр содержимого документа
«ОГЭ 2023 Февраль Математика Вариант 2»
1. Задание 1 № 406563
Определите, какие месяцы соответствуют указанному в таблице трафику мобильного интернета.
Заполните таблицу, в бланк ответов перенесите числа, соответствующие номерам месяцев, без пробелов, запятых и других дополнительных символов (например, для месяцев май, январь, ноябрь, август в ответе нужно записать
число 51118).
| Мобильный интернет | 2,5 Гб | 3 Гб | 3,25 Гб | 1 Гб |
| Номер месяца |
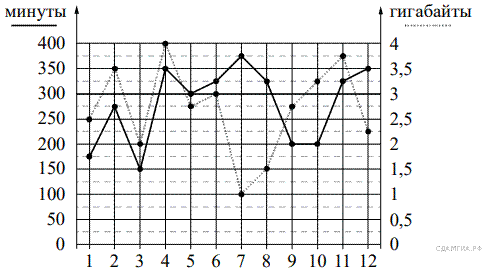
На рисунке точками показано количество минут исходящих вызовов и трафик мобильного интернета в гигабайтах, израсходованных абонентом в процессе пользования смартфоном, за каждый месяц 2019 года. Для удобства точки, соответствующие минутам и гигабайтам, соединены сплошными и пунктирными линиями соответственно.
В течение года абонент пользовался тарифом «Стандартный», абонентская плата по которому составляла 350 рублей в месяц. При условии нахождения абонента на территории РФ в абонентскую плату тарифа «Стандартный» входит:
• пакет минут, включающий 300 минут исходящих вызовов на номера, зарегистрированные на территории РФ;
• пакет интернета, включающий 3 гигабайта мобильного интернета;
• пакет СМС, включающий 120 СМС в месяц;
• безлимитные бесплатные входящие вызовы.
Стоимость минут, интернета и СМС сверх пакета тарифа указана в таблице.
| Исходящие вызовы | 3 руб./мин. |
| Мобильный интернет (пакет) | 90 руб. за 0,5 Гб |
| СМС | 2 руб./шт. |
Абонент не пользовался услугами связи в роуминге. За весь год абонент отправил 110 СМС.
Решение.
Пунктирной линей на графике показан трафик мобильного интернета в гигабайтах, израсходованных за каждый месяц года.
Из рисунка видно, что 2,5 Гб было потрачено в первый месяц, 3 Гб — потрачено в шестой, 3,25 Гб — в десятый, 1 Гб — в седьмой.
Ответ: 16107.
2. Задание 2 № 406675
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику израсходованных минут и гигабайтов.
| ПЕРИОДЫ | ХАРАКТЕРИСТИКИ | |
| А) январь−февраль Б) февраль−март В) август–сентябрь Г) ноябрь–декабрь |
1) Расход минут увеличился, а расход гигабайтов уменьшился. 2) Расход гигабайтов увеличился, а расход минут уменьшился. 3) Расход минут увеличился, и расход гигабайтов увеличился. 4) Расход минут уменьшился, и расход гигабайтов уменьшился. |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Решение.
Пунктирной линей на графике показан трафик мобильного интернета в гигабайтах, израсходованных за каждый месяц года, а сплошной линей — количество минут исходящих вызовов.
За период январь−февраль расход минут увеличился, и расход гигабайтов увеличился.
За период февраль−март расход минут уменьшился, и расход гигабайтов уменьшился.
За период август–сентябрь расход гигабайтов увеличился, а расход минут уменьшился.
За период ноябрь–декабрь расход минут увеличился, а расход гигабайтов уменьшился.
Таким образом, получается соответствие: А — 3, Б — 4, В — 2, Г — 1.
Ответ: 3421.
3. Задание 3 № 406564
Сколько рублей потратил абонент на услуги связи в июне?
Решение.
По рисунку видно, что за июнь абонент потратил 3 Гб интернета, 325 минут исходящих вызовов, и в условии сказано, что за год отправил 110 СМС.
Количество потраченного интернета и СМС не превысило это количество в пакете тарифа, а исходящих вызовов сверх пакета было потрачено 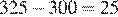
Вычислим стоимость услуг связи, потраченных абонентом в июне:
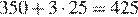
Ответ: 425.
4. Задание 4 № 406565
Какое наименьшее количество минут исходящих вызовов за месяц было в 2019 году?
Решение.
Сплошной линей на графике показано количество минут исходящих вызовов, израсходованных за каждый месяц года.
Из рисунка видно, что в третьем месяце было потрачено 150 минут, что является наименьшим количеством за 2019 год.
Ответ: 150.
5. Задание 5 № 367694
Компания выбирает место для строительства торгово‐развлекательного комплекса: на месте квартала старых одноэтажных домов в центре города или на окраине города. Стоимость прокладки 1 метра коммуникаций равна 6000 рублей. В аренду планируется сдавать 4000 м2 площади комплекса. Стоимость земли, цена строительства комплекса с учётом сноса старых зданий и предполагаемая стоимость сдачи даны в таблице.
| Место | Цена земли (млн руб.) | Цена строительства (млн руб.) | Длина коммуникаций (м) | Стоимость аренды за 1 м2 (руб./месяц) |
| Центр | 64,4 | |||
| Окраина | 11,2 |
Обдумав оба варианта, компания выбрала местом для строительства центр города. Через сколько месяцев после начала сдачи в аренду торговых площадей построенного комплекса более высокая стоимость аренды компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций? Ответ округлите до целых.
На плане (см. рисунок) изображён район города, в котором живёт Петя. Сторона каждой клетки на плане равна 10 м.
Дом, в котором живёт Петя, обозначен цифрой 6. Прямо напротив дома, где живёт Петя, через дорогу находится дом в форме буквы «Г», где живёт его друг Вася. Рядом с домом, где живёт Петя, расположен дом, где живёт одноклассница Таня, а напротив него через дорогу имеется здание банка площадью 600 м2. А с другой стороны дома, где живёт Таня, расположен детский сад. Недалеко от детского сада и дома, где живёт Петя, находится магазин. Также имеется автобусная остановка, обозначенная цифрой 4, а в десяти метрах от неё — квартал старых одноэтажных домов.
Решение.
Стоимость постройки ТРК в центре города равна
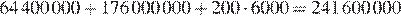
Стоимость постройки ТРК на окраине города равна
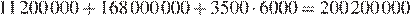
Разница в стоимости составляет
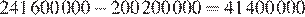
Разница в стоимости аренды составляет
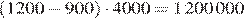
Значит, более высокая стоимость аренды компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций через 34,5 месяцев. Округляя, получаем ответ — 35 месяцев.
Ответ: 35.
6. Задание 6 № 203743
Запишите в ответе номера выражений, значения которых положительны.
Номера запишите в порядке возрастания без пробелов, запятых и других дополнительных символов.
Решение.
Найдём значения выражений:
Таким образом, искомое выражение указано под номером 3.
7. Задание 7 № 314800
На координатной прямой отмечены числа а и b. Какое из следующих утверждений неверно?
В ответе укажите номер правильного варианта.
1)
2)
3)
4)
Решение.
Заметим, что 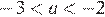
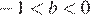
1) 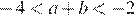
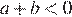
2) 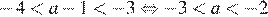
3) 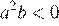
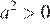
4) 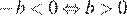
Неверным является утверждение 4.
Примечание.
Нетрудно заметить, что справедливо неравенство:
8. Задание 8 № 341704
Найдите значение выражения 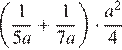
Решение.
Упростим выражение:
Подставим в полученное выражение значение
Ответ: 0,66.
9. Задание 9 № 338610
Решите уравнение
Решение.
Последовательно получаем:
Ответ: −6.
10. Задание 10 № 325541
Стрелок 3 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что стрелок первые 2 раза попал в мишени, а последний раз промахнулся.
Решение.
Вероятность того, что стрелок промахнётся равна 1 − 0,8 = 0,2. Вероятность того, что стрелок первые два раза попал по мишеням равна 0,82 = 0,64. Откуда, вероятность события, при котором стрелок сначала два раза попадает в мишени, а третий раз промахивается равна 0,64 · 0,2 = 0,128.
Ответ: 0,128.
11. Задание 11 № 193089
Найдите значение 
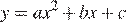
Решение.
Абсцисса вершины параболы равна −1, поэтому 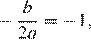
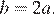
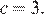
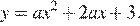
Верный ответ указан под номером 2.
Ответ: 2.
12. Задание 12 № 338396
Расстояние s (в метрах) до места удара молнии можно приближённо вычислить по формуле s = 330t, где t — количество секунд, прошедших между вспышкой молнии и ударом грома. Определите, на каком расстоянии от места удара молнии находится наблюдатель, если t = 10 с. Ответ дайте в километрах, округлив его до целых.
Решение.
Найдем расстояние, на котором находится наблюдатель от места удара молнии:
Ответ: 3.
13. Задание 13 № 311312
Решите неравенство 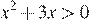
В ответе укажите номер правильного варианта.
1)
2)
3)
4)
Решение.
Решим данное неравенство:
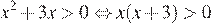
В данном случае это выполняется при следующих значениях 
1) 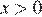
2) 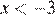
Решением неравенства будет являться объединение этих промежутков: 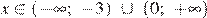
Ответ: 1
14. Задание 14 № 394426
Давление воздуха под колоколом равно 625 мм ртутного столба. Каждую минуту насос откачивает из-под колокола 20% находящегося там воздуха. Определите давление (в мм рт. ст.) через 5 минут после начала работы насоса.
Решение.
Через минуту давление воздуха (в мм рт. ст.) под колоколом станет 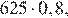
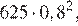
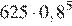
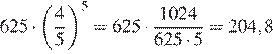
Ответ: 204,8.
15. Задание 15 № 348371
Высота BH ромба ABCD делит его сторону AD на отрезки AH = 44 и HD = 11. Найдите площадь ромба.
Решение.
Заметим, что сторона ромба AB = AD = AH + HD = 44 + 11 = 55.
Из прямоугольного треугольника ABH найдем BH по теореме Пифагора:
Площадь ромба можно найти как произведение основания на высоту:
Ответ: 1815.
16. Задание 16 № 339975
Отрезок AB = 40 касается окружности радиуса 75 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
Решение.
Радиус окружности перпендикулярен касательной в точке касания. Из прямоугольного треугольника 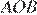
Найдём 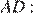
Ответ: 10.
17. Задание 17 № 324017

Решение.

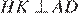
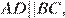
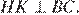
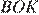
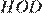
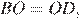
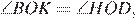
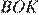
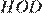

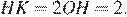
Ответ: 18.
18. Задание 18 № 311485
На квадратной сетке изображён угол 
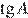
Решение.
Опустим перпендикуляр BH. Треугольник ABH — прямоугольный. Таким образом,
Ответ: 3.
19. Задание 19 № 341676
Какие из следующих утверждений верны?
1) Треугольника со сторонами 1, 2, 4 не существует.
2) Смежные углы равны.
3) Все диаметры окружности равны между собой.
Если утверждений несколько, запишите их номера в порядке возрастания.
Решение.
1) «Треугольника со сторонами 1, 2, 4 не существует» — верно, большая сторона треугольника должна быть меньше суммы двух других.
2) «Смежные углы равны» — неверно, смежные углы 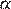
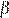
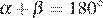
3) «Все диаметры окружности равны между собой» — верно.
Ответ: 13.
20. Задание 20 № 311591
Решите уравнение:
Решение.
Перенесем все члены влево и применим формулу разности квадратов:
Другой способ. Раскроем скобки, пользуясь формулой квадрата разности:
Ответ: 1.
21. Задание 21 № 314507
Из пункта А в пункт В, расстояние между которыми 13 км, вышел пешеход. Одновременно с ним из В в А выехал велосипедист. Велосипедист ехал со скоростью, на 11 км/ч большей скорости пешехода, и сделал в пути получасовую остановку. Найдите скорость пешехода, если известно, что они встретились в 8 км от пункта В.
Решение.
Пусть скорость пешехода — x км/ч, 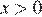
Составим таблицу по данным задачи:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| Пешеход | 
|
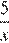
|
|
| Велосипедист | 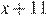
|
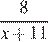
|
Так как по пути велосипедист сделал остановку на 
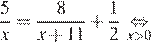
Корень −22 не подходит нам по условию задачи. Скорость пешехода равна 5 км/ч.
Ответ: 5 км/ч.
22. Задание 22 № 353274
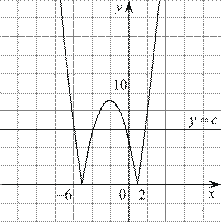
Постройте график функции 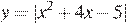
Решение.
График данной функции — это график параболы 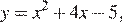
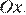
Прямая, параллельная оси абсцисс задаётся формулой 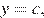


Ответ: 4.
23. Задание 23 № 333321
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB = 10, DC = 25, AC = 56 .
Решение.

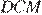
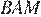
Значит, 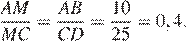
Откуда
Ответ: 40.
24. Задание 24 № 349626
Окружности с центрами в точках 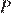
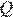
Решение.
Проведём построения и введём обозначения, как показано на рисунке. Пусть 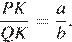
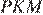
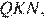
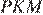
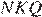
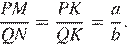
25. Задание 25 № 311708
В прямоугольном треугольнике ABC с прямым углом B, проведена биссектриса угла A. Известно, что она пересекает серединный перпендикуляр, проведённый к стороне BC в точке K. Найдите угол BCK, если известно, что угол ACB равен 40°.
Решение.
Так как биссектриса острого угла A прямоугольного треугольника ABC не может быть перпендикулярна BC, то биссектриса угла A и серединный перпендикуляр к BC имеют ровно одну общую точку.
Пусть N — середина BC. Рассмотрим окружность, описанную около треугольника ABC. Пусть серединный перпендикуляр к BC пересекает меньшую дугу BC в точке L (см. рисунок), тогда точка L является серединой этой дуги, ⌣BL = ⌣LC. Но тогда 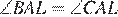
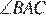
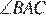
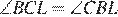
Пусть 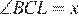
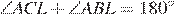
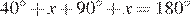
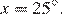
Ответ: 25°.
1.
2.
Задача 1 (№1-№5)
3.
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на
схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
На плане (см. рисунок) изображён район города, в котором живёт Петя. Сторона каждой
клетки на плане равна 10 м.
Дом, в котором живёт Петя, обозначен цифрой 6. Прямо напротив дома, где живёт Петя,
через дорогу находится дом в форме буквы «Г», где живёт его друг Вася. Рядом с домом,
где живёт Петя, расположен дом, где живёт одноклассница Таня, а напротив него через
дорогу имеется здание банка площадью 600 м2. А с другой стороны дома, где живёт Таня,
расположен детский сад. Недалеко от детского сада и дома, где живёт Петя, находится
магазин. Также имеется автобусная остановка, обозначенная цифрой 4, а в десяти метрах
от неё — квартал старых одноэтажных домов.
Решение.
Рядом с домом, где живёт Петя, расположен дом, где живёт одноклассница Таня, а
напротив него через дорогу имеется здание банка площадью 600 м2. Значит, Банк отмечен
цифрой 3, а дом, где живёт Таня, отмечен цифрой 2. Недалеко от детского сада и дома, где
живёт Петя, находится магазин, следовательно, магазин отмечен цифрой 5. Также имеется
автобусная остановка, обозначенная цифрой 4, а в десяти метрах от неё — квартал старых
одноэтажных домов, значит, квартал старых домой обозначен цифрой 8.
Объекты Банк Магазин Дом, где живёт Квартал старых
Таня
домов
Цифры
4.
2. Территорию стадиона необходимо засеять газонной травой. В одной
упаковке газонной травы содержится 12 кг семян, при этом для
засеивания 3 м2 земли необходимо 100 г семян. Какое минимальное
количество упаковок газонной травы необходимо приобрести?
Решение.
Найдём площадь стадиона: 1клетка=10м, 4клетки=10•4м, 8клеток=10•8м
м2.
Значит, для того, чтобы засеять стадион, понадобится
кг семян.
106,7 : 12 = 8,88 приближенно округляем до целых 9 упаковок
Таким образом, чтобы засеять стадион газонной травой, требуется купить
9 упаковок газонной травы.
О т ве т: 9.
5.
3. Найдите суммарную площадь, которую занимают дома, где
проживают Таня, Петя и Вася. Ответ дайте в м2.
Решение.
Площадь дома, в котором живёт Петя, равна
м2.
Площадь дома, в котором живёт Таня, равна
м2.
Площадь дома, в котором живёт Вася, равна
м2.
Таким образом, суммарная площадь домов, где проживают Таня, Петя и
Вася равна
м2.
Ответ: 6900.
6.
4. Найдите расстояние от дома, где живёт Петя, до автобусной
остановки (расстояние между двумя ближайшими точками по прямой) в
метрах.
Решение.
Найдём расстояние между двумя ближайшими точками по прямой дома
Пети и автобусной остановки по теореме Пифагора:
От ве т: 130.
7.
5. Компания выбирает место для строительства торгово‐развлекательного комплекса:
на месте квартала старых одноэтажных домов в центре города или на окраине города.
Стоимость прокладки 1 метра коммуникаций равна 6000 рублей. В аренду планируется
сдавать 4000 м2 площади комплекса. Стоимость земли, цена строительства комплекса с
учётом сноса старых зданий и предполагаемая стоимость сдачи даны в таблице.
Место
Центр
Цена
Длина
Стоимость
Цена земли
строительства коммуникаций аренды за 1 м2
(млн руб.)
(млн руб.)
(м)
(руб./месяц)
64,4
176
200
1200
Окраина
11,2
168
3500
900
Обдумав оба варианта, компания выбрала местом для строительства центр города. Через сколько
месяцев после начала сдачи в аренду торговых площадей построенного комплекса более высокая
стоимость аренды компенсирует разность в стоимости земли, строительства и прокладывания
коммуникаций? Ответ округлите до целых.
Решение.
Стоимость постройки ТРК в центре города равна
рублей.
Стоимость постройки ТРК на окраине города равна
рублей.
Разница в стоимости составляет
рублей.
Разница в стоимости аренды составляет
рублей
41 400 000 : 1 200 000 = 34,5 месяцев округляем 35 месяцев.
Значит, более высокая стоимость аренды компенсирует разность в стоимости земли,
строительства и прокладывания коммуникаций через 34,5 месяцев. Округляя, получаем ответ — 35
месяцев.
О т в е т : 35.
8.
Задача 2 (№1-№5).
9.
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на
плане. Заполните таблицу, в ответ запишите последовательность четырёх цифр без
пробелов и других дополнительных символов.
На плане (см. рисунок) изображена местность, прилегающая к озеру Круглому. Для
удобства план нанесён на квадратную сетку, сторона каждого квадрата которой равна 500
м. Населённые пункты обозначены на плане жирными точками.
Рядом с озером Круглое находится болото, обозначенное на плане штриховкой. На
болоте расположен хутор Камышино. От хутора Камышино проложена дорога к деревне
Дубки, вокруг которой имеются дубовые рощи. Далее дорога идёт к селу Большое,
расположенному по другую сторону озера от хутора Камышино. Село Большое соединено
также дорогой с деревней Малая, обозначенной на плане цифрой 7. Деревня Малая, в свою
очередь, соединена дорогой с деревней Дальней (отмечена цифрой 4). Преобладающая
часть изображённой на плане местности — это поля, используемые для выращивания
злаков.
Решение.
Рядом с озером Круглое находится болото, обозначенное на плане штриховкой. На
болоте расположен хутор Камышино, значит, хутор Камышино отмечен на плане цифрой
2. На плане (см. рисунок) изображена местность, прилегающая к озеру Круглому, значит,
озеро Круглое отмечено цифрой 5. От хутора Камышино проложена дорога к деревне
Дубки, вокруг которой имеются дубовые рощи, следовательно, деревня Дубки отмечена
цифрой 1. Далее, от деревни Дубки, дорога идёт к селу Большое, расположенному по
другую сторону озера от хутора Камышино, поэтому село Большое отмечено цифрой 6.
Объекты Хутор Камышино Село Большое Озеро Круглое Деревня Дубки
Цифры
10.
2. Автомобиль расходует в среднем 9 л топлива на 100 км пути. Сколько литров
топлива израсходует автомобиль при поездке из хутора Камышино в деревню Малая
по имеющимся дорогам?
Решение.
Сторона каждого квадрата равна 500 м. От хутора Камышино до деревни
Дубки 6 клеток. От деревни Дубки до села Большого 8 клеток. От села
Большого до деревни Малая 6 клеток. Значит, расстояние, которое нужно
проехать, равно
Чтобы проехать один километр, понадобится
Значит, при поездке из хутора Камышино
понадобится
л.
в
литров бензина.
деревню Малая
11.
3. Найдите площадь (в км2) болота, отмеченного на плане.
Решение.
Сторона одной клетки равна 500 м. Значит, площадь болота равна:
Ответ: 3,75.
12.
4. Найдите расстояние (в метрах) по прямой от хутора
Камышино до села Большое.
Решение.
Сторона одной клетки равна 500 м. Значит, расстояние по прямой
от хутора Камышино до села Большое по теореме Пифагора:
Ответ: 5000.
13.
5. Для улучшения сообщения между населёнными пунктами планируется
построить ещё одну дорогу: из хутора Камышино в деревню Малая либо из хутора
Камышино в деревню Дальняя. Дорога должна соединить населённые пункты по
прямой. Цена прокладки дороги по полю равна 10 млн рублей за 1 км, по болоту – 20
млн рублей за 1 км. Из указанных двух вариантов дороги выберете тот, стоимость
которого будет ниже. В ответе укажите стоимость (в млн рублей) выбранного
варианта дороги.
Решение.
Сторона одной клетки равна 500 м. Значит, 1 км дороги из хутора Камышино в деревню
Малая будет проходить по болоту, а другие 3 км — по полю. Следовательно, стоимость
дороги из хутора Камышино в деревню Малая равна
млн рублей.
Далее, 2 км дороги из хутора Камышино в деревню Дальняя будет проходить по болоту,
а 0,5 км — по полю. Следовательно, стоимость дороги из хутора Камышино в деревню
Дальняя равна
млн рублей.
Таким образом, стоимость дороги из хутора Камышино в деревню Дальняя меньше и
равна 45 млн рублей. Ответ: 45
14.
Спасибо
за внимание!
14
Бесплатные консультации
по юридическим и бухгалтерским вопросам. Задавайте вопросы профессионалам и получите, понятный ответ и решение вашей проблемы.
- Мы вам поможем:
- Право
- Бухгалтерия
- ИП
- ООО
- И много другое
5 000 000 консультаций
Более пяти миллионов консультаций, от профессионалов в своих областях.
100 категорий, права
Опыт во всех областях: от гражданского права до уголовного, от ИП до ООО
Полный ответ на вопрос
Выделим тезисы, порекомендуем документы и сошлемся на статьи РФ.
Категории вопросов
Выберите категорию вопроса
«Баркли» может построить крупный апарт-комплекс рядом с торговым центром «Авиапарк»
Это будет первый проект девелопера за последние несколько лет
К рискам нового комплекса консультанты относят и высокую конкуренцию в этом районе / Максим Стулов / Ведомости
Компания «Специализированный застройщик (СЗ) «М-девелопмент» попросила градостроительно-земельную комиссию Москвы (ГЗК) внести изменения в правила землепользования и застройки участка за торгово-развлекательным комплексом (ТРК) «Авиапарк» на Ходынском бульваре (между ТРК и парком «Ходынское поле»). Это следует из документов ГЗК, с которыми ознакомились «Ведомости». Площадь этой территории, согласно данным Росрееста, составляет 1,69 га. Ранее Москомстройинвест сообщал, что там планируется строительство 130 000 кв. м недвижимости. Один из консультантов, работавших с этой площадкой, уточняет, что проект должен включать в себя гостиницу на 74 000 кв. м, многофункциональный комплекс на 46 000 кв. м, а также Центр современного искусства на 10 000 кв. м.
Изначально девелопером этой площадки выступал собственник «Авиапарка» – АО «ТВК «Авиапарк». Ранее конечными бенефициарами этой компании консультанты называли бизнесмена Михаила Зайца, совладельца Amma Development (строила этот торговый центр), и структуры семьи Аркадия Ротенберга (сначала его самого, потом сына Игоря, а затем дочь Лилию). Но СЗ «М-девелопмент», который подал заявку в ГЗК на согласование нового проекта за «Авиапарком», может быть связан с девелоперской компанией «Баркли» Леонида Казинца.
По крайней мере, согласно «СПАРК-Интерфаксу», в России зарегистрировано лишь две компании с таким названием. Первая находится под управлением «Баркли», директором второй выступает Казинец. Сам он подтверждать свое участие в проекте у «Авиапарка» не стал, сообщив, что «это какая-то ошибка или совпадение». Правда, два консультанта, работавших с данной площадкой, знают, что «Баркли» «договорилась с владельцами «Авиапарка» о застройке участка рядом с ТРК». Один из них утверждает, что стороны заключили или в ближайшее время планируют заключить сделку по приобретению площадки. По его словам, «Баркли» хочет согласовать тут строительство или апартаментов, или гостинично-апартаментного комплекса.