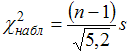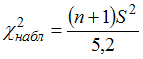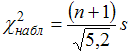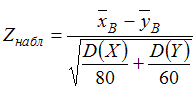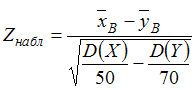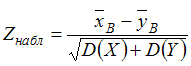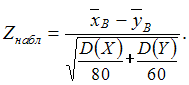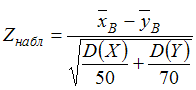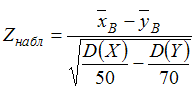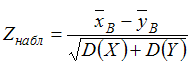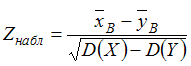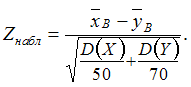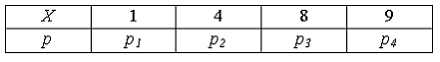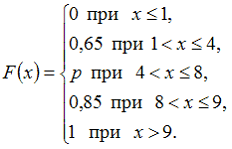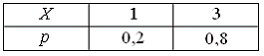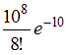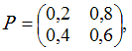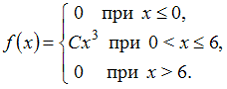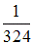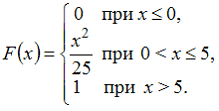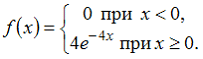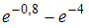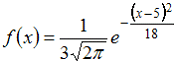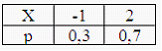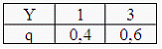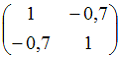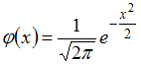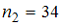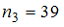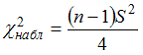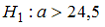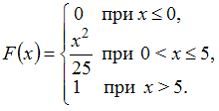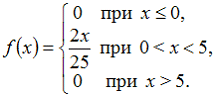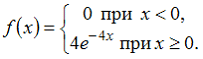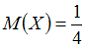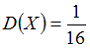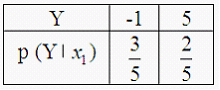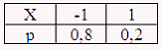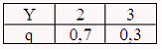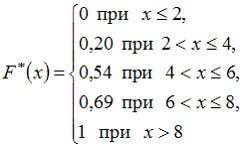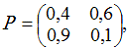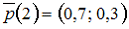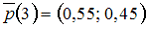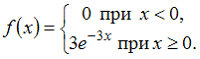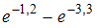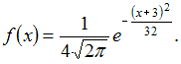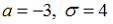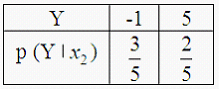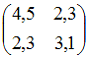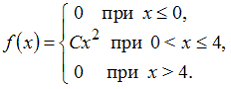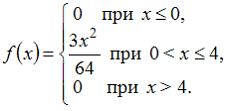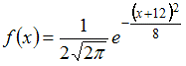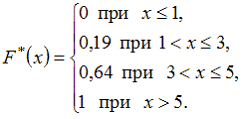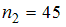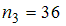1. Левосторонняя
критическая область может определяться
из соотношения …
Решение:Левосторонней
называют критическую область, определяемую
соотношением
,
где–
отрицательное число, а–
уровень значимости. Таким соотношением
является.
3. Соотношением
вида
можно
определить …
левостороннюю
критическую область
правостороннюю
критическую область
двустороннюю
критическую область
область принятия
гипотезы
Решение:Данное
соотношение определяет левостороннюю
критическую область, так как левосторонней
называют критическую область, определяемую
соотношением
,
где–
положительное число, а–
уровень значимости.
4. Соотношением
вида
можно
определить …
двустороннюю
критическую область
правостороннюю
критическую область
левостороннюю
критическую область
область принятия
гипотезы
Решение:Данное
соотношение определяет двустороннюю
критическую область, так как двусторонней
называют критическую область, определяемую,
например, соотношением вида
,
где–
положительное число, а–
уровень значимости.
Тема 35: Проверка гипотез о дисперсиях
1. Основная гипотеза
имеет вид
Тогда
конкурирующей может являться гипотеза …
Решение:Конкурирующей
(альтернативной) называют гипотезу,
которая противоречит основной гипотезе.
Условию
противоречит
3. Основная гипотеза
имеет вид
Тогда
конкурирующей может являться гипотеза …
Решение:Конкурирующей
(альтернативной) называют гипотезу,
которая противоречит основной гипотезе.
Условию
противоречит
4. Наблюдаемое
значение критерия проверки гипотезы
о
равенстве неизвестной генеральной
дисперсии нормальной совокупности
гипотетическому (предполагаемому)
значениюможет
иметь вид …
Решение:Для
проверки гипотезы
о
равенстве неизвестной генеральной
дисперсии нормальной совокупности
гипотетическому (предполагаемому)
значениюприменяется
статистический критерий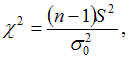
имеет хи-квадрат распределение сстепенями
свободы, где–
объем выборки, по которой вычисляется
исправленная дисперсия.
Тема 36: Проверка гипотез о математических ожиданиях
1. Основная гипотеза
имеет вид
Тогда
конкурирующей может являться гипотеза …
Решение:Конкурирующей
(альтернативной) называют гипотезу,
которая противоречит основной гипотезе.
Условию
противоречит
2. Наблюдаемое
значение критерия проверки гипотезы
о
равенстве средних двух нормальных
генеральных совокупностей с известными
дисперсиямии
может
иметь вид …
Решение:Для
проверки гипотезы
о
равенстве средних двух нормальных
генеральных совокупностей с известными
дисперсиямии
применяется
статистический критерий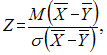
имеет стандартное нормальное распределение.
Тогда наблюдаемое значение критерия
определяется как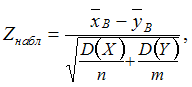
и
–
объемы независимых выборок, по которым
вычислены выборочные средниеи
соответственно.
Следовательно, например, при,
получаем
3. Наблюдаемое
значение критерия проверки гипотезы
о
равенстве средних двух нормальных
генеральных совокупностей с известными
дисперсиямии
может
иметь вид …
Решение:Для
проверки гипотезы
о
равенстве средних двух нормальных
генеральных совокупностей с известными
дисперсиямии
применяется
статистический критерий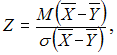
имеет стандартное нормальное распределение.
Тогда наблюдаемое значение критерия
определяется как
и
–
объемы независимых выборок, по которым
вычислены выборочные средниеи
соответственно.
Следовательно, например, при,
получаем
Кейс 1 подзадача 1
1. Курсовая стоимость
ценной бумаги равна 1000 рублей. Она может
в течение недели подорожать на 4 % с
вероятностью 0,9 или подешеветь на 4 %
с вероятностью 0,1. Предполагается, что
еженедельные изменения цен независимы.
Прошло две недели.Установите
соответствие между случайными событиями
и вероятностями этих событий.
1. Курс
ценной бумаги упадет
2. Курс ценной
бумаги вырастет
3. Курс ценной бумаги
не изменится
0,19
0,81
0
0,01
0,18
Решение:Пусть
событие
заключается
в том, что стоимость ценной бумаги в
течение недели вырастет на 4 % доруб.,
а событиезаключается
в том, что стоимость ценной бумаги в
течение недели упадет на 4 % доруб.
Следовательно,
1) вероятность того,
что курс ценной бумаги за две недели
упадет, определяется как вероятность
событиято
есть равнатак
как2)
вероятность того, что курс ценной бумаги
за две недели вырастет, определяется
как вероятность событиято
есть равна3)
вероятность того, что курс ценной бумаги
за две недели не изменится, равна нулю,
так как соответствующее событие является
невозможным.
2. Курсовая стоимость
ценной бумаги равна 1000 рублей. Она может
в течение недели подорожать на 6 % с
вероятностью 0,75 или подешеветь на 6 %
с вероятностью 0,25. Предполагается, что
еженедельные изменения цен независимы.
Прошло две недели.Установите
соответствие между случайными событиями
и вероятностями этих событий.
1. Курс
ценной бумаги упадет
2. Курс ценной
бумаги вырастет
3. Курс ценной бумаги
не изменится
0,4375
0,5625
0
0,0625
0,375
Решение:Пусть
событие
заключается
в том, что стоимость ценной бумаги в
течение недели вырастет на 6 % доруб.,
а событиезаключается
в том, что стоимость ценной бумаги в
течение недели упадет на 6 % доруб.
Следовательно,
1) вероятность того,
что курс ценной бумаги за две недели
упадет, определяется как вероятность
событиято
есть равнатак
как2)
вероятность того, что курс ценной бумаги
за две недели вырастет, определяется
как вероятность событиято
есть равна3)
вероятность того, что курс ценной бумаги
за две недели не изменится, равна нулю,
так как соответствующее событие является
невозможным.
3. Курсовая стоимость
ценной бумаги равна 1000 рублей. Она может
в течение недели подорожать на 5 % с
вероятностью 0,8 или подешеветь на 5 %
с вероятностью 0,2. Предполагается, что
еженедельные изменения цен независимы.
Прошло две недели.Установите
соответствие между случайными событиями
и вероятностями этих событий.
1. Курс
ценной бумаги упадет
2. Курс ценной
бумаги вырастет
3. Курс ценной бумаги
не изменится
0,36
0,64
0
0,04
0,32
Решение:Пусть
событие
заключается
в том, что стоимость ценной бумаги в
течение недели вырастет на 5 % доруб.,
а событиезаключается
в том, что стоимость ценной бумаги в
течение недели упадет на 5 % доруб.
Следовательно,
1) вероятность того,
что курс ценной бумаги за две недели
упадет, определяется как вероятность
событиято
есть равнатак
как2)
вероятность того, что курс ценной бумаги
за две недели вырастет, определяется
как вероятность событиято
есть равна3)
вероятность того, что курс ценной бумаги
за две недели не изменится, равна нулю,
так как соответствующее событие является
невозможным.
4. Курсовая стоимость
ценной бумаги равна 1000 рублей. Она может
в течение недели подорожать на 2 % с
вероятностью 0,6 или подешеветь на 2 %
с вероятностью 0,4. Предполагается, что
еженедельные изменения цен независимы.
Прошло две недели.Установите
соответствие между случайными событиями
и вероятностями этих событий.
1. Курс
ценной бумаги упадет
2. Курс ценной
бумаги вырастет
3. Курс ценной бумаги
не изменится
0,64
0,36
0
0,16
0,24
Решение:Пусть
событие
заключается
в том, что стоимость ценной бумаги в
течение недели вырастет на 2 % доруб.,
а событиезаключается
в том, что стоимость ценной бумаги в
течение недели упадет на 2 % доруб.
Следовательно,
1) вероятность того,
что курс ценной бумаги за две недели
упадет, определяется как вероятность
событиято
есть равнатак
как2)
вероятность того, что курс ценной бумаги
за две недели вырастет, определяется
как вероятность событиято
есть равна3)
вероятность того, что курс ценной бумаги
за две недели не изменится, равна нулю,
так как соответствующее событие является
невозможным.
Кейс 1 подзадача 2
1. Курсовая стоимость
ценной бумаги равна 1000 рублей. Она может
в течение недели подорожать на 4 % с
вероятностью 0,9 или подешеветь на 4 %
с вероятностью 0,1. Предполагается, что
еженедельные изменения цен независимы.
Прошло две недели.Максимально
возможный курс ценной бумаги будет
принадлежать интервалам (в руб.) …
(1081,5; 1082,5)
(1081,0; 1082,0)
(1080,5; 1081,5)
(1080,0; 1081,0)
Решение:Определим
максимально возможный курс ценной
бумаги как
руб.
Тогда из предложенных ответов правильными
будут ответы: (1081,5; 1082,5) и (1081,0; 1082,0).
2. Курсовая стоимость
ценной бумаги равна 1000 рублей. Она может
в течение недели подорожать на 6 % с
вероятностью 0,75 или подешеветь на 6 %
с вероятностью 0,25. Предполагается, что
еженедельные изменения цен независимы.
Прошло две недели.Максимально
возможный курс ценной бумаги будет
принадлежать интервалам (в руб.) …
(1123,5; 1127,5)
(1121,5; 1125,0)
(1118,5; 1122,5)
(1115,5; 1121,0)
Решение:Определим
максимально возможный курс ценной
бумаги как
руб.
Тогда из предложенных ответов правильными
будут ответы: (1123,5; 1127,5) и (1121,5; 1125,0).
3. Курсовая стоимость
ценной бумаги равна 1000 рублей. Она может
в течение недели подорожать на 5 % с
вероятностью 0,8 или подешеветь на 5 %
с вероятностью 0,2. Предполагается, что
еженедельные изменения цен независимы.
Прошло две недели.Максимально
возможный курс ценной бумаги будет
принадлежать интервалам (в руб.) …
(1101,0; 1103,4)
(1100,4; 1103,0)
(1099,9; 1102,4)
(1099,4; 1102,0)
Решение:Определим
максимально возможный курс ценной
бумаги как
руб.
Тогда из предложенных ответов правильными
будут ответы: (1101,0; 1103,4) и (1100,4; 1103,0).
4. Курсовая стоимость
ценной бумаги равна 1000 рублей. Она может
в течение недели подорожать на 2 % с
вероятностью 0,6 или подешеветь на 2 %
с вероятностью 0,4. Предполагается, что
еженедельные изменения цен независимы.
Прошло две недели.Максимально
возможный курс ценной бумаги будет
принадлежать интервалам (в руб.) …
(1040,0; 1041,0)
(1039,5; 1040,5)
(1039,0; 1040,0)
(1038,5; 1039,5)
Решение:Определим
максимально возможный курс ценной
бумаги как
руб.
Тогда из предложенных ответов правильными
будут ответы:
(1040,0; 1041,0) и (1039,5; 1040,5).
Кейс 1 подзадача 3
1. Курсовая стоимость
ценной бумаги равна 1000 рублей. Она может
в течение недели подорожать на 4 % с
вероятностью 0,9 или подешеветь на 4 %
с вероятностью 0,1. Предполагается, что
еженедельные изменения цен независимы.
Прошло две недели.Математическое
ожидание курсовой стоимости ценой
бумаги будет равно …
1065,024
1065,00
1064,976
1000,00
Решение:Составим
закон распределения вероятностей
дискретной случайной величины
–
курсовой стоимости ценной бумаги,
как
а
Тогда
2. Курсовая стоимость
ценной бумаги равна 1000 рублей. Она может
в течение недели подорожать на 6 % с
вероятностью 0,75 или подешеветь на 6 %
с вероятностью 0,25. Предполагается, что
еженедельные изменения цен независимы.
Прошло две недели.Математическое
ожидание курсовой стоимости ценой
бумаги будет равно …
1060,90
1060,00
1059,10
1000,00
Решение:Составим
закон распределения вероятностей
дискретной случайной величины
–
курсовой стоимости ценной бумаги,
как:
а
Тогда
3. Курсовая стоимость
ценной бумаги равна 1000 рублей. Она может
в течение недели подорожать на 5 % с
вероятностью 0,8 или подешеветь на 5 %
с вероятностью 0,2. Предполагается, что
еженедельные изменения цен независимы.
Прошло две недели.Математическое
ожидание курсовой стоимости ценой
бумаги будет равно …
1060,90
1050,00
1059,10
1000,00
Решение:Составим
закон распределения вероятностей
дискретной случайной величины
–
курсовой стоимости ценной бумаги,
как
а
Тогда
4. Курсовая стоимость
ценной бумаги равна 1000 рублей. Она может
в течение недели подорожать на 2 % с
вероятностью 0,6 или подешеветь на 2 %
с вероятностью 0,4. Предполагается, что
еженедельные изменения цен независимы.
Прошло две недели.Математическое
ожидание курсовой стоимости ценой
бумаги будет равно …
1008,016
1008,00
1007,944
1000,00
Решение:Составим
закон распределения вероятностей
дискретной случайной величины
–
курсовой стоимости ценной бумаги,
как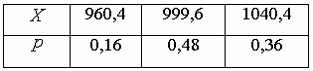
а
Тогда
Кейс 2 подзадача 1
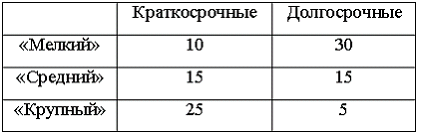
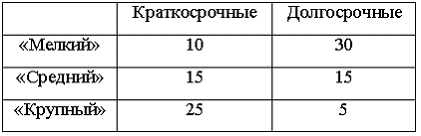
1. Кредитный отдел
банка проанализировал выданные кредиты
по двум параметрам (в % от общего числа
кредитов): по величине и срокам.

того, что кредит краткосрочный, если он
«средний», можно оценить как …
Решение:Вероятность
того, что кредит краткосрочный, если он
«средний», можно оценить как
2. Кредитный отдел
банка проанализировал выданные кредиты
по двум параметрам (в % от общего числа
кредитов): по величине и срокам.
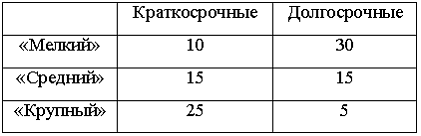
того, что кредит краткосрочный, если он
«крупный», можно оценить как …
Решение:Вероятность
того, что кредит краткосрочный, если он
«крупный», можно оценить как
3. Кредитный отдел
банка проанализировал выданные кредиты
по двум параметрам (в % от общего числа
кредитов): по величине и срокам.
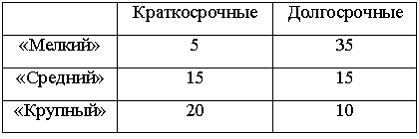
того, что кредит долгосрочный, если он
«мелкий», можно оценить как …
Решение:Вероятность
того, что кредит долгосрочный, если он
«мелкий», можно оценить как
Кейс 2 подзадача 2
1. Кредитный отдел
банка проанализировал выданные кредиты
по двум параметрам (в % от общего числа
кредитов): по величине и срокам.

долгосрочный кредит. Установите
соответствие между видом кредита и
вероятностью его выдачи.
1. «Крупный»
2.
«Средний»
3. «Мелкий»
Решение:1.
Вероятность того, что кредит «крупный»,
если он долгосрочный, можно оценить как
2.
Вероятность того, что кредит «средний»,
если он долгосрочный, можно оценить как3.
Вероятность того, что кредит «мелкий»,
если он долгосрочный, можно оценить как
2. Кредитный отдел
банка проанализировал выданные кредиты
по двум параметрам (в % от общего числа
кредитов): по величине и срокам.
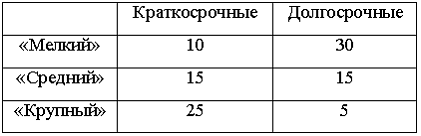
краткосрочный кредит. Установите
соответствие между видом кредита и
вероятностью его выдачи.
1. «Крупный»
2.
«Средний»
3. «Мелкий»
Решение:1.
Вероятность того, что кредит «крупный»,
если он краткосрочный, можно оценить
как
2.
Вероятность того, что кредит «средний»,
если он краткосрочный, можно оценить
как3.
Вероятность того, что кредит «мелкий»,
если он краткосрочный, можно оценить
как
3. Кредитный отдел
банка проанализировал выданные кредиты
по двум параметрам (в % от общего числа
кредитов): по величине и срокам.
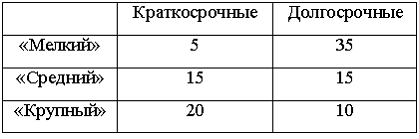
краткосрочный кредит. Установите
соответствие между видом кредита и
вероятностью его выдачи.
1. «Крупный»
2.
«Средний»
3. «Мелкий»
Решение:1.
Вероятность того, что кредит «крупный»,
если он краткосрочный, можно оценить
как
2.
Вероятность того, что кредит «средний»,
если он краткосрочный, можно оценить
как3.
Вероятность того, что кредит «мелкий»,
если он краткосрочный, можно оценить
как
Кейс 2 подзадача 3
1. Кредитный отдел
банка проанализировал выданные кредиты
по двум параметрам (в % от общего числа
кредитов): по величине и срокам.
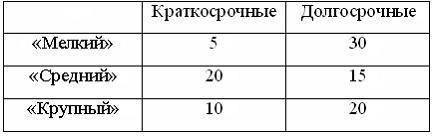
рассматриваемом периоде банк выдал 100
кредитов. Если средний размер кредита
«Мелкий» был равен 100 тыс. руб., кредита
«Средний» – 700 тыс. руб., кредита «Крупный»
– 2 млн руб., то объем кредитного портфеля
банка составит ____ млн руб.
Решение:Объем
кредитного портфеля банка составит:

руб.
2. Кредитный отдел
банка проанализировал выданные кредиты
по двум параметрам (в % от общего числа
кредитов): по величине и срокам.
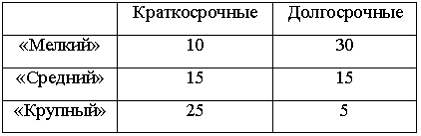
рассматриваемом периоде банк выдал 100
кредитов. Если средний размер кредита
«Мелкий» был равен 100 тыс. руб., кредита
«Средний» – 400 тыс. руб., кредита «Крупный»
– 2 млн руб., то объем кредитного портфеля
банка составит ____ млн руб.
Решение:Объем
кредитного портфеля банка составит:
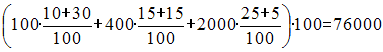
руб., или 76 млн. руб.
3. Кредитный отдел
банка проанализировал выданные кредиты
по двум параметрам (в % от общего числа
кредитов): по величине и срокам.
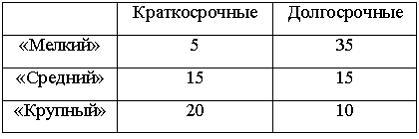
рассматриваемом периоде банк выдал 100
кредитов. Если средний размер кредита
«Мелкий» был равен 100 тыс. руб., кредита
«Средний» – 600 тыс. руб., кредита «Крупный»
– 2 млн руб., то объем кредитного портфеля
банка составит ____ млн руб.
Решение:Объем
кредитного портфеля банка составит:
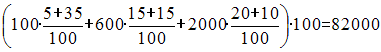
руб., или 82 млн руб.
Кейс 3 подзадача 1
1. Компания
рассматривает проект по строительству
трех домов, по одному в разных районах
города. Средства для строительства дают
сами будущие жильцы. Вероятность набрать
необходимые средства для постройки
одного дома составляет 0,6. Каждый
построенный дом окупает 80 % всех
затрат компании по проекту, равных 500
млн руб.Предположим,
что собранных средств будет достаточно
для строительства k
домов. Установите соответствие между
значениями k
и вероятностями соответствующих
случайных событий.
1.
k = 1
2. k
= 2
3. k
= 3
0,288
0,432
0,216
0,6
0,36
Решение:Пусть
случайная величина
–
количество домов, построенных компанией.
Воспользуемся формулой Бернуллигде
Тогда:
1)2)
3)
2. Компания
рассматривает проект по строительству
трех домов, по одному в разных районах
города. Средства для строительства дают
сами будущие жильцы. Вероятность набрать
необходимые средства для постройки
одного дома составляет 0,9. Каждый
построенный дом окупает 50 % всех
затрат компании по проекту, равных 500
млн руб.Предположим,
что собранных средств будет достаточно
для строительства k
домов. Установите соответствие между
значениями k
и вероятностями соответствующих
случайных событий.
1.
k = 1
2. k
= 2
3. k
= 3
0,027
0,243
0,729
0,9
0,81
Решение:Пусть
случайная величина
–
количество домов, построенных компанией.
Воспользуемся формулой Бернуллигде
Тогда:
1)2)
3)
3. Компания
рассматривает проект по строительству
трех домов, по одному в разных районах
города. Средства для строительства дают
сами будущие жильцы. Вероятность набрать
необходимые средства для постройки
одного дома составляет 0,8. Каждый
построенный дом окупает 60 % всех
затрат компании по проекту, равных 500
млн руб.Предположим,
что собранных средств будет достаточно
для строительства k
домов. Установите соответствие между
значениями k
и вероятностями соответствующих
случайных событий.
1.
k = 1
2. k
= 2
3. k
= 3
0,096
0,384
0,512
0,8
0,64
Решение:Пусть
случайная величина
–
количество домов, построенных компанией.
Воспользуемся формулой Бернуллигде
Тогда:
1)2)
3)
4. Компания
рассматривает проект по строительству
трех домов, по одному в разных районах
города. Средства для строительства дают
сами будущие жильцы. Вероятность набрать
необходимые средства для постройки
одного дома составляет 0,7. Каждый
построенный дом окупает 70 % всех
затрат компании по проекту, равных 500
млн руб.Предположим,
что собранных средств будет достаточно
для строительства k
домов. Установите соответствие между
значениями k
и вероятностями соответствующих
случайных событий.
1. k
= 1
2. k
= 2
3. k
= 3
0,189
0,441
0,343
0,7
0,49
Решение:Пусть
случайная величина
–
количество домов, построенных компанией.
Воспользуемся формулой Бернуллигде
Тогда:
1)2)
3)
Кейс 3 подзадача 2
1. Компания
рассматривает проект по строительству
трех домов, по одному в разных районах
города. Средства для строительства дают
сами будущие жильцы. Вероятность набрать
необходимые средства для постройки
одного дома составляет 0,6. Каждый
построенный дом окупает 80 % всех
затрат компании по проекту, равных 500
млн руб.Если
обозначить через
количество
построенных компанией домов, то случайную
величинуS
– прибыль компании (в млн руб.) – можно
определить как …
Решение:Так
как каждый построенный дом окупает 80%
всех затрат по проекту, а именно
млн
руб., то прибыль компании можно определить
как
2. Компания
рассматривает проект по строительству
трех домов, по одному в разных районах
города. Средства для строительства дают
сами будущие жильцы. Вероятность набрать
необходимые средства для постройки
одного дома составляет 0,9. Каждый
построенный дом окупает 50 % всех
затрат компании по проекту, равных 500
млн руб.Если
обозначить через
количество
построенных компанией домов, то случайную
величинуS
– прибыль компании (в млн руб.) – можно
определить как …
Решение:Так
как каждый построенный дом окупает 50%
всех затрат по проекту, а именно
млн
руб., то прибыль компании можно определить
как
3. Компания
рассматривает проект по строительству
трех домов, по одному в разных районах
города. Средства для строительства дают
сами будущие жильцы. Вероятность набрать
необходимые средства для постройки
одного дома составляет 0,8. Каждый
построенный дом окупает 60 % всех
затрат компании по проекту, равных 500
млн руб.Если
обозначить через
количество
построенных компанией домов, то случайную
величинуS
– прибыль компании (в млн руб.) – можно
определить как …
Решение:Так
как каждый построенный дом окупает 60%
всех затрат по проекту, а именно
млн
руб., то прибыль компании можно определить
как
4. Компания
рассматривает проект по строительству
трех домов, по одному в разных районах
города. Средства для строительства дают
сами будущие жильцы. Вероятность набрать
необходимые средства для постройки
одного дома составляет 0,7. Каждый
построенный дом окупает 70 % всех
затрат компании по проекту, равных 500
млн руб.Если
обозначить через
количество
построенных компанией домов, то случайную
величинуS
– прибыль компании (в млн руб.) – можно
определить как …
Решение:Так
как каждый построенный дом окупает 70%
всех затрат по проекту, а именно
млн
руб., то прибыль компании можно определить
как
Кейс 3 подзадача 3
1. Компания
рассматривает проект по строительству
трех домов, по одному в разных районах
города. Средства для строительства дают
сами будущие жильцы. Вероятность набрать
необходимые средства для постройки
одного дома составляет 0,6. Каждый
построенный дом окупает 80 % всех
затрат компании по проекту, равных 500
млн руб.Ожидаемая
прибыль компании равна ____ млн руб.
Решение:Составим
закон распределения случайной величины
S
– прибыли компании:

ожидаемая прибыль компании равнамлн
руб.
2. Компания
рассматривает проект по строительству
трех домов, по одному в разных районах
города. Средства для строительства дают
сами будущие жильцы. Вероятность набрать
необходимые средства для постройки
одного дома составляет 0,9. Каждый
построенный дом окупает 50 % всех
затрат компании по проекту, равных 500
млн руб.Ожидаемая
прибыль компании равна ____ млн руб.
Решение:Составим
закон распределения случайной величины
S
– прибыли компании:

ожидаемая прибыль компании равнамлн
руб.
3. Компания
рассматривает проект по строительству
трех домов, по одному в разных районах
города. Средства для строительства дают
сами будущие жильцы. Вероятность набрать
необходимые средства для постройки
одного дома составляет 0,8. Каждый
построенный дом окупает 60 % всех
затрат компании по проекту, равных 500
млн руб.Ожидаемая
прибыль компании равна ____ млн руб.
Решение:Составим
закон распределения случайной величины
S
– прибыли компании:

ожидаемая прибыль компании равнамлн
руб.
4. Компания
рассматривает проект по строительству
трех домов, по одному в разных районах
города. Средства для строительства дают
сами будущие жильцы. Вероятность набрать
необходимые средства для постройки
одного дома составляет 0,7. Каждый
построенный дом окупает 70 % всех
затрат компании по проекту, равных 500
млн руб.Средняя
ожидаемая прибыль компании равна ____
млн руб.
Решение:Составим
закон распределения случайной величины
S
– прибыли компании:

ожидаемая прибыль компании равнамлн
руб.
Компания рассматривает проект по строительству трех домов, по одному в разных районах города. Средства для строительства дают сами будущие жильцы. Вероятность набрать необходимые средства для постройки одного дома составляет 0,9. Каждый построенный дом окупает 50 % всех затрат компании по проекту, равных 500 млн руб.
Предположим, что собранных средств будет достаточно для строительства k домов. Установите соответствие между значениями k и вероятностями соответствующих случайных событий.
1. k = 1
2. k = 2
3. k = 3
Варианты для выбора соответствия: Выберите соответствие:
- 0,027
- 0,243
- 0,81
- 0,9
- 0,729
Внимание!
Верный ответ отмечен зелёным цветом.
Загрузка ответа…
Если через несколько секунд ответ не появился, то проверьте соединение с интернетом и нажмите на кнопку
Тесты по Теории вероятностей и математической статистики
| Содержание |
Тесты от института.
1. В круг радиуса 8 помещен меньший круг радиуса 5. Тогда вероятность того, что точка, наудачу брошенная в больший круг, попадет также и в меньший круг, равна …
— ! 25/64
2. Операции сложения и умножения событий не обладают свойством …
— ! А-В = В-А
3. Вероятность поражения цели первым стрелком равна 0,95, а вторым – 0,80. Оба стрелка стреляют одновременно. Тогда вероятность того, что цель будет поражена только одним стрелком, равна …
— !! 0,23
4. Банк выдает 40% всех кредитов юридическим лицам, а 60% – физическим лицам. Вероятность того, что юридическое лицо не погасит в срок кредит, равна 0,1; а для физического лица эта вероятность составляет 0,05. Получено сообщение о невозврате кредита. Тогда вероятность того, что этот кредит не погасило физическое лицо, равна …
— !! 3/7
5. Дискретная случайная величина X задана законом распределения вероятностей:
Тогда вероятность 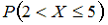
— !! 0,25
6. Для дискретной случайной величины X:
функция распределения вероятностей имеет вид:
Тогда значение параметра p может быть равно …
— !! 0,7
7. Дискретная случайная величина X задана законом распределения вероятностей:
Тогда ее среднее квадратическое отклонение равно …
— !! 0,80
8. Проводится n независимых испытаний, в каждом из которых вероятность появления события A постоянна и равна 0,6. Тогда математическое ожидание M(X) и дисперсия D(X) дискретной случайной величины X – числа появлений события A в n=100 проведенных испытаниях – равны …
— M(X)=60, D(X)=24
9. Среднее число заявок, поступающих на предприятие бытового обслуживания за 1 час равно пяти. Тогда вероятность того, что за два часа поступит восемь заявок, можно вычислить как …
—
10. Матрица вероятностей перехода однородной цепи Маркова имеет вид
а вектор начального распределения вероятностей – 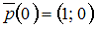
Тогда вектор вероятностей состояний цепи Маркова на втором шаге равен …
— p(2) = (0,36; 0,64)
11. Непрерывная случайная величина X задана плотностью распределения вероятностей:
Тогда значение параметра C равно …
—
12. Непрерывная случайная величина X задана функцией распределения вероятностей:
Тогда вероятность 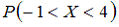
— 16/25
13. Непрерывная случайная величина X задана плотностью распределения вероятностей:
Тогда ее дисперсия равна …
— 25/18
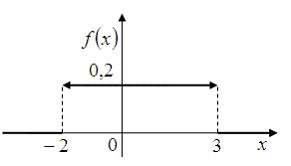
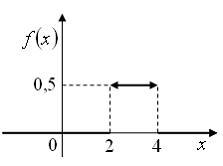
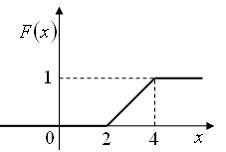
14. Дан график плотности распределения вероятностей непрерывной случайной величины X :
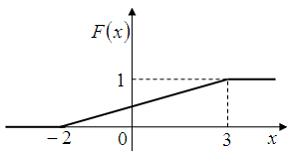
Тогда график ее функции распределения вероятностей имеет вид …
—
15. Случайная величина X распределена по показательному закону с плотностью распределения вероятностей
Тогда вероятность 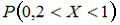
—
16. Случайная величина X распределена нормально с математическим ожиданием M(X)=5 и дисперсией D(X)=9 Тогда ее плотность распределения вероятностей имеет вид …
—
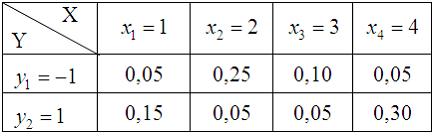
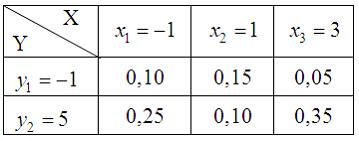
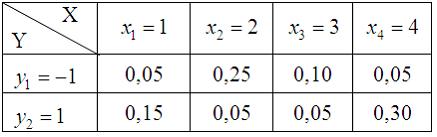
17. Двумерная дискретная случайная величина (X, Y) задана законом распределения вероятностей:
Тогда вероятность 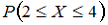
— 0,80
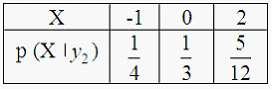
18. Двумерная дискретная случайная величина (X, Y) задана законом распределения вероятностей:
Тогда условный закон распределения вероятностей составляющей X при условии, что составляющая Y приняла значение y2=6, имеет вид …
—
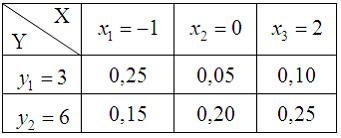
19. Дискретные случайные величины X и Y заданы законами распределения вероятностей:
Тогда закон распределения вероятностей функции Z=X+Y имеет вид …
—
20. Корреляционная матрица для системы случайных величин (X, Y) может иметь вид …
—
21. Математическое ожидание случайной величины X равно M(X)=52, а дисперсия – D(X)=24. Тогда вероятность того, что 32<X<72, можно оценить с использованием неравенства Чебышева как …
— P=0,94
22. Вероятность появления события A в каждом из 800 проведенных испытаний равна 0,4. Тогда вероятность того, что относительная частота появлений события A будет заключена в пределах от 0,38 до 0,42, можно оценить с использованием неравенства Бернулли как …
— (? ?) P=0,25
— (—>) P≥0,25
23. Вероятность появления некоторого события в каждом из 400 независимых испытаний постоянна и равна 0,1. Тогда вероятность того, что событие появится ровно 52 раза, следует вычислять как …
— 
24. Вероятность того, что деталь не пройдет проверку ОТК, равна 0,15. Тогда вероятность того, что среди 300 случайно отобранных деталей окажется не менее 50 деталей, не прошедших проверку ОТК, следует вычислить по …
— интегральной формуле Лапласа
25. Из генеральной совокупности извлечена выборка объема n=81:
Тогда значение n3 равно …
— 34
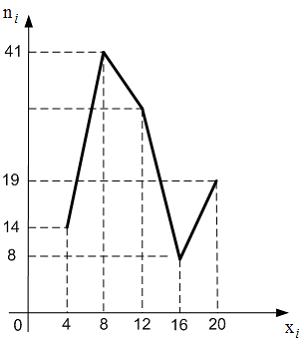
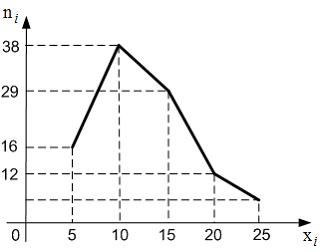
26. Из генеральной совокупности извлечена выборка объема n=114, полигон частот которой имеет вид:
Тогда число вариант xi=12 в выборке равно …
— 32
27. Медиана вариационного ряда 11, 14, 16, 17, 17, 17, 18, 19, 21, 22, 22, 23, 25, 25 равна …
— 18,5
28. Из генеральной совокупности X извлечена выборка объема n=100:
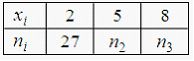
эмпирическая функция распределения вероятностей которой имеет вид:
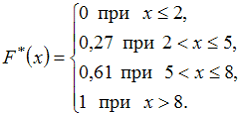
Тогда …
—
29. Дан доверительный интервал (20,145;21,755) для оценки математического ожидания нормально распределенного количественного признака. Тогда точность этой оценки равна …
— 0,805
30. Из генеральной совокупности извлечена выборка объема n=20:
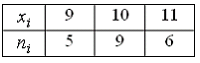
Тогда несмещенная оценка математического ожидания равна …
— 10,05
31. В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 3,6; 3,8; 4,3. Тогда несмещенная оценка дисперсии равна …
— 0,13
32. Дан доверительный интервал (32,06;41,18) для оценки математического ожидания нормально распределенного количественного признака. Тогда точечная оценка математического ожидания равна …
— 36,62
33. Выборочное уравнение прямой линии регрессии Y на X имеет вид y=2,7+0,6x, а выборочные средние квадратические отклонения равны: 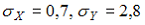
— 0,15
34. Соотношением вида 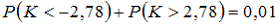
— двустороннюю критическую область
35. Наблюдаемое значение критерия проверки гипотезы 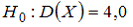
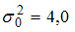
—
36. Основная гипотеза имеет вид 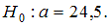
—
37. Курсовая стоимость ценной бумаги равна 1000 рублей. Она может в течение недели подорожать на 4 % с вероятностью 0,9 или подешеветь на 4 % с вероятностью 0,1. Предполагается, что еженедельные изменения цен независимы. Прошло две недели.
Установите соответствие между случайными событиями и вероятностями этих событий.
— Курс ценной бумаги упадет — 0,19
— Курс ценной бумаги вырастет — 0,81
— Курс ценной бумаги не изменится — 0
— нет соответствия — 0,01
— нет соответствия — 0,18
38. Курсовая стоимость ценной бумаги равна 1000 рублей. Она может в течение недели подорожать на 5 % с вероятностью 0,8 или подешеветь на 5 % с вероятностью 0,2. Предполагается, что еженедельные изменения цен независимы. Прошло две недели.
Максимально возможный курс ценной бумаги будет принадлежать интервалам (в руб.) …
— (1101,0; 1103,4)
— (1100,4; 1103,0)
39. Курсовая стоимость ценной бумаги равна 1000 рублей. Она может в течение недели подорожать на 5 % с вероятностью 0,8 или подешеветь на 5 % с вероятностью 0,2. Предполагается, что еженедельные изменения цен независимы. Прошло две недели.
Математическое ожидание курсовой стоимости ценой бумаги будет равно …
— 1060,90
40. Кредитный отдел банка проанализировал выданные кредиты по двум параметрам (в % от общего числа кредитов): по величине и срокам.
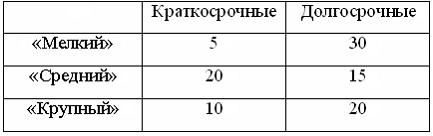
Вероятность того, что кредит краткосрочный, если он «средний», можно оценить как …
— 4/7
41. Кредитный отдел банка проанализировал выданные кредиты по двум параметрам (в % от общего числа кредитов): по величине и срокам.
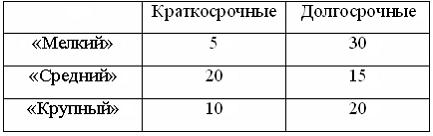
Выдан долгосрочный кредит. Установите соответствие между видом кредита и вероятностью его выдачи.
— «крупный» — 4/13
— «средний» — 3/13
— «мелкий» — 6/13
— не имеет соответсвия — 4/7
— не имеет соответсвия — 2/7
42. Кредитный отдел банка проанализировал выданные кредиты по двум параметрам (в % от общего числа кредитов): по величине и срокам.
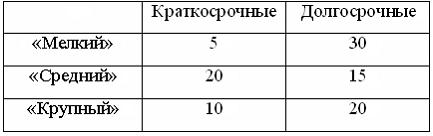
В рассматриваемом периоде банк выдал 100 кредитов. Если средний размер кредита «Мелкий» был равен 100 тыс. руб., кредита «Средний» – 700 тыс. руб., кредита «Крупный» – 2 млн руб., то объем кредитного портфеля банка составит ____ млн руб.
— 88
43. Компания рассматривает проект по строительству трех домов, по одному в разных районах города. Средства для строительства дают сами будущие жильцы. Вероятность набрать необходимые средства для постройки одного дома составляет 0,7. Каждый построенный дом окупает 70 % всех затрат компании по проекту, равных 500 млн руб.
Предположим, что собранных средств будет достаточно для строительства k домов. Установите соответствие между значениями k и вероятностями соответствующих случайных событий.
— k = 1 — 0,189
— k = 2 — 0,441
— k = 3 — 0,343
— нет соответствия — 0,7
— нет соответствия — 0,49
44. Компания рассматривает проект по строительству трех домов, по одному в разных районах города. Средства для строительства дают сами будущие жильцы. Вероятность набрать необходимые средства для постройки одного дома составляет 0,8. Каждый построенный дом окупает 60 % всех затрат компании по проекту, равных 500 млн руб.
Если обозначить через X количество построенных компанией домов, то случайную величину S – прибыль компании (в млн руб.) – можно определить как …
— S=300*X-500
45. Компания рассматривает проект по строительству трех домов, по одному в разных районах города. Средства для строительства дают сами будущие жильцы. Вероятность набрать необходимые средства для постройки одного дома составляет 0,6. Каждый построенный дом окупает 80 % всех затрат компании по проекту, равных 500 млн руб.
Ожидаемая прибыль компании равна ____ млн руб.
— 220
93% отлично
13.14.20.23.26.27.35.
46. В партии из 12 деталей имеется 5 бракованных. Наудачу отобраны три детали. Тогда вероятность того, что среди отобранных деталей нет годных, равна …
— 1/22
47. Два студента сдают экзамен. Если ввести события A (экзамен успешно сдал первый студент) и B (экзамен успешно сдал второй студент), то событие, заключающееся в том, что экзамен сдадут успешно оба студента, будет представлять собой выражение …
— А*В
48. В урну, в которой лежат 6 белых и 5 черных шаров добавляют два черных шара. После этого наудачу по одному извлекают три шара без возвращения. Тогда вероятность того, что хотя бы один шар будет белым, равна …
— 251/286
49. Банк выдает 35% всех кредитов юридическим лицам, а 65% – физическим лицам. Вероятность того, что юридическое лицо не погасит в срок кредит, равна 0,15; а для физического лица эта вероятность составляет 0,1. Тогда вероятность непогашения в срок очередного кредита равна …
— 0,1175
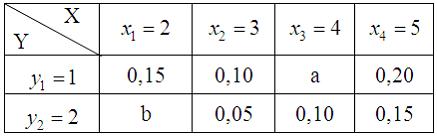
50. Дискретная случайная величина X задана законом распределения вероятностей:

Тогда значения a и b могут быть равны …
— a=0,35 b=0,2
51. Дискретная случайная величина X задана законом распределения вероятностей:

Тогда ее функция распределения вероятностей имеет вид …
— 
52. Дискретная случайная величина X задана законом распределения вероятностей:

Тогда ее дисперсия равна …
— 0,96
53. Банк выдал пять кредитов. Вероятность того, что кредит не будет погашен в срок, равна 0,1. Тогда вероятность того, что в срок не будут погашены три кредита, равна …
— 0,0081
54. Среднее число заявок, поступающих на предприятие бытового обслуживания за 1 час, равно трем. Тогда вероятность того, что за два часа поступит пять заявок, можно вычислить как …
—
55. Матрица вероятностей перехода однородной цепи Маркова имеет вид
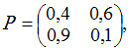
а вектор вероятностей состояний цепи Маркова на втором шаге равен p(2)=(0,3; 0,7).
Тогда вектор вероятностей состояний цепи Маркова на третьем шаге равен …
— p(3)=(0,75; 0,25)
56. Непрерывная случайная величина X задана плотностью распределения вероятностей:
Тогда вероятность P(1<X<3) равна …
— 1/2
57. Непрерывная случайная величина задана функцией распределения вероятностей:
Тогда ее плотность распределения вероятностей имеет вид …
—
58. Случайная величина распределена по показательному закону с плотностью распределения вероятностей
Тогда ее математическое ожидание и дисперсия равны …
—
59. Непрерывная случайная величина X задана плотностью распределения вероятностей
Тогда математическое ожидание a и среднее квадратическое отклонение σ этой случайной величины равны …
— a =4, σ =2
60. Двумерная дискретная случайная величина (X, Y) задана законом распределения вероятностей:
Тогда значения a и b могут быть равны …
— a =0,10; b =0,15
61. Двумерная дискретная случайная величина (X, Y) задана законом распределения вероятностей:
Тогда условный закон распределения вероятностей составляющей Y при условии, что составляющая X приняла значение x1=-1, равно …
— !!
62. Дискретные случайные величины X и Y заданы законами распределения вероятностей:
Тогда закон распределения вероятностей функции Z=X*Y имеет вид …
—
63. Вероятность выигрыша по одному лотерейному билету равна 0,3. Всего было куплено 200 билетов. Тогда вероятность того, что количество выигравших билетов будет заключено в пределах от 50 до 70, можно оценить с использованием неравенства Чебышева как …
— (? ?) P =0,58
— (—>) P ≥0,58
64. Вероятность появления некоторого события в каждом из 400 независимых испытаний постоянна и равна 0,8. Тогда вероятность того, что событие появится не менее 300 и не более 328 раз, следует вычислять как …
— 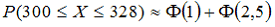
65. Статистическое распределение выборки имеет вид
Тогда объем выборки равен …
— 67
66. Из генеральной совокупности X извлечена выборка объема n =100:
Тогда ее эмпирическая функция распределения вероятностей F*(x) имеет вид …
—
67. Дан доверительный интервал (16,64; 18,92) для оценки математического ожидания нормально распределенного количественного признака. Тогда при увеличении объема выборки этот доверительный интервал может принять вид …
— (17,18; 18,38)
68. Проведено пять измерений (без систематических ошибок) некоторой случайной величины (в мм): 4,5; 5,2; 6,1; 7,8, 8,3. Тогда несмещенная оценка математического ожидания равна …
— 6,38
69. В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 15; 18; 21; 24. Тогда выборочная дисперсия равна …
— 11,25
70. Точечная оценка вероятности биномиально распределенного количественного признака равна 0,38. Тогда его интервальная оценка может иметь вид …
— (0,25; 0,51)
71. При построении выборочного уравнения парной регрессии вычислены выборочный коэффициент корреляции rB=0,54 и выборочные средние квадратические отклонения σX=1,6; σY=3,2. Тогда выборочный коэффициент регрессии Y на X равен …
— 0,27
72. Левосторонняя критическая область может определяться из соотношения …
— P(K < -1,72)=0,05
73. Основная гипотеза имеет вид H0:a=18,5. Тогда конкурирующей может являться гипотеза …
— H1:a≠18,5
74. Курсовая стоимость ценной бумаги равна 1000 рублей. Она может в течение недели подорожать на 2 % с вероятностью 0,6 или подешеветь на 2 % с вероятностью 0,4. Предполагается, что еженедельные изменения цен независимы. Прошло две недели.
Установите соответствие между случайными событиями и вероятностями этих событий.
— 0,36 __ Курс ценной бумаги вырастет
— 0 __ Курс ценной бумаги не изменится
— 0,64 __ Курс ценной бумаги упадет
— 0,16 __ не имеет соответствия
— 0,24 __ не имеет соответствия
Нет результата
47.3.49.5.51.53.9.11.12.13.17.19.63.22.
75. Игральная кость бросается два раза. Тогда вероятность того, что сумма выпавших очков – семь, а разность – три, равна …
— 1/18
76. Дискретная случайная величина X задана законом распределения вероятностей:
—
77. Матрица вероятностей перехода однородной цепи Маркова имеет вид
а вектор вероятностей состояний цепи Маркова на втором шаге равен
. Тогда вектор вероятностей состояний цепи Маркова на третьем шаге равен …
—
78. Дан график плотности распределения вероятностей непрерывной случайной величины X:
Тогда график ее функции распределения вероятностей имеет вид …
—
79. Случайная величина X распределена по показательному закону с плотностью распределения вероятностей
Тогда вероятность 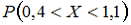
—
80. Непрерывная случайная величина X задана плотностью распределения вероятностей
Тогда математическое ожидание a и среднее квадратическое отклонение σ этой случайной величины равны …
—
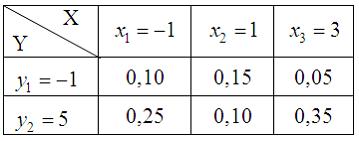
81. Двумерная дискретная случайная величина (X, Y) задана законом распределения вероятностей:
Тогда условный закон распределения вероятностей составляющей Y при условии, что составляющая X приняла значение x2= 1, имеет вид …
— !!!
82. Ковариационная матрица для системы случайных величин (X, Y) может иметь вид …
— ?
Нет результат
1.2.5.51.9.55.12.14.79.61.62.82.63.22.23.24.25.27.72.35.37.42.44.
83. В урну, в которой лежат 6 белых и 5 черных шаров добавляют два белых шара. После этого наудачу по одному извлекают три шара без возвращения. Тогда вероятность того, что все три шара будут белыми, равна …
— 28/143
84. В первой урне 3 черных шара и 7 белых шаров. Во второй урне 4 белых шара и 6 черных шаров. Из наудачу взятой урны вынули один шар, который оказался черным. Тогда вероятность того, что этот шар вынули из второй урны, равна …
— 2/3
85. Проводится n независимых испытаний, в каждом из которых вероятность появления события A постоянна и равна 0,8. Тогда математическое ожидание M(X) и дисперсия D(X) дискретной случайной величины X – числа появлений события A в n=200 проведенных испытаниях – равны …
— M(X) =160, D(X) =32
86. Непрерывная случайная величина X задана плотностью распределения вероятностей:
Тогда значение параметра C равно …
— 3/64
87. Непрерывная случайная величина X задана плотностью распределения вероятностей:
Тогда ее математическое ожидание равно …
— 3
88. Случайная величина X распределена нормально с математическим ожиданием M(X)= -12 и дисперсией D(X)= 4 Тогда ее плотность распределения вероятностей имеет вид …
—
89. Двумерная дискретная случайная величина задана законом распределения вероятностей:
Тогда вероятность 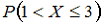
— 0,45
90. Из генеральной совокупности извлечена выборка объема n = 100, полигон частот которой имеет вид:
Тогда относительная частота варианты xi s= 25 в выборке равна …
— 0,05
91. Из генеральной совокупности извлечена выборка объема n= 100:
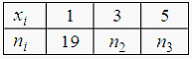
эмпирическая функция распределения вероятностей которой имеет вид:
Тогда …
—
92. Дан доверительный интервал (12,44; 14,68) для оценки математического ожидания нормально распределенного количественного признака. Тогда точность этой оценки равна …
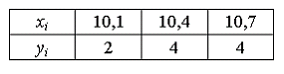
— 1,12
93. Из генеральной совокупности извлечена выборка объема n= 50:
Тогда несмещенная оценка математического ожидания равна …
— 13,14
94. Из генеральной совокупности извлечена выборка объема n= 10:
Тогда выборочное среднее квадратическое отклонение равно …
—
95. Точечная оценка математического ожидания нормально распределенного количественного признака равна 0,4. Тогда его интервальная оценка может иметь вид …
— (-0,05; 0,85)
96. Выборочное уравнение прямой линии регрессии Y на X имеет вид y= -4,8+1,2x. Тогда выборочный коэффициент корреляции может быть равен …
— 0,82
97. Наблюдаемое значение критерия проверки гипотезы H0 : M(X) = M(Y) о равенстве средних двух нормальных генеральных совокупностей с известными дисперсиями D(X) и D(Y) может иметь вид …
—
98. Курсовая стоимость ценной бумаги равна 1000 рублей. Она может в течение недели подорожать на 6 % с вероятностью 0,75 или подешеветь на 6 % с вероятностью 0,25. Предполагается, что еженедельные изменения цен независимы. Прошло две недели.
Максимально возможный курс ценной бумаги будет принадлежать интервалам (в руб.) …
— (1123,5; 1127,5)
— (1121,5; 1125,0)
99. Курсовая стоимость ценной бумаги равна 1000 рублей. Она может в течение недели подорожать на 2 % с вероятностью 0,6 или подешеветь на 2 % с вероятностью 0,4. Предполагается, что еженедельные изменения цен независимы. Прошло две недели.
Математическое ожидание курсовой стоимости ценой бумаги будет равно …
— 1008,016
100. Кредитный отдел банка проанализировал выданные кредиты по двум параметрам (в % от общего числа кредитов): по величине и срокам.
Вероятность того, что кредит краткосрочный, если он «крупный», можно оценить как …
— 5/6
101. Кредитный отдел банка проанализировал выданные кредиты по двум параметрам (в % от общего числа кредитов): по величине и срокам.
Выдан краткосрочный кредит. Установите соответствие между видом кредита и вероятностью его выдачи.
— 1/2 — Крупный
— 3/10 — Средний
— 2/10 — Мелкий
— 2/5 — иное
— 3/5 — иное
102. Компания рассматривает проект по строительству трех домов, по одному в разных районах города. Средства для строительства дают сами будущие жильцы. Вероятность набрать необходимые средства для постройки одного дома составляет 0,9. Каждый построенный дом окупает 50 % всех затрат компании по проекту, равных 500 млн руб.
Предположим, что собранных средств будет достаточно для строительства k домов. Установите соответствие между значениями k и вероятностями соответствующих случайных событий.
— k = 1 — 0,027
— k = 2 — 0,243
— k = 3 — 0,729
— 0,9 — нет соответствия
— 0,81 — нет соответствия
103. Компания рассматривает проект по строительству трех домов, по одному в разных районах города. Средства для строительства дают сами будущие жильцы. Вероятность набрать необходимые средства для постройки одного дома составляет 0,9. Каждый построенный дом окупает 50 % всех затрат компании по проекту, равных 500 млн руб.
Ожидаемая прибыль компании равна ____ млн руб.
— 175
98% отлично
2._.48.4._.6.
104. В партии из 12 деталей имеется 5 бракованных. Наудачу отобраны три детали. Тогда вероятность того, что среди отобранных деталей нет бракованных, равна …
— 7/44
105. Дискретная случайная величина X задана законом распределения
вероятностей:
Тогда вероятность 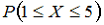
— 0,7
106.
—
107.
—
10.
—
| … |
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5