Компания по страхованию автомобилей разделяет водителей по трем классам класс а мало рискует

Задача 2.

Электролампы изготавливаются на трех заводах. Первый завод производит 45% общего количества электроламп, второй – 40%, третий – 15%. Продукция первого завода содержит 70% стандартных ламп, второго – 80%, третьего – 81%. В магазин поступает продукция всех трех заводов. Какова вероятность того, что купленная в магазине лампа стандартная.

Решение.

А = {купленная в магазине лампа стандартная}, Н1 = {лампа с первого завода}, Н2 = {лампа со второго завода}, Н3 = {лампа с третьего завода}.

Р(Н1) = 0,45; Р(Н2) = 0,4; Р(Н3) = 0,15.

Р(А/Н1) = 0,7; Р(А/Н2) = 0,8; Р(А/Н3) = 0,81.

P( A) = 0,45× 0,7 + 0,4× 0,8 + 0,15× 0,81 = 0,7565.

Задача 3.

Агентство по страхованию автомобилей разделяет водителей по трем классам: 1 класс – мало рискуют, 2 класс – рискуют средне, 3 класс – сильно рискуют. Из всех водителей, застраховавших автомобили, 30% принадлежат к классу 1, 50% — к классу 2 и 20% — к классу 3. Вероятность того, что в течение года водитель класса 1 попадет хотя бы в одну аварию, равна 0,01; для водителя класса 2 вероятность равна 0,02; для водителя третьего класса – 0,08. Водитель страхует свою машину и в течение года попадает в аварию. Какова вероятность того, что он относится к классу 1? К классу 2? К классу 3?

Решение.

А = {водитель попадает в аварию}. Н1 = {водитель относится к 1 классу}, Н2 = {водитель относится к 2 классу}, Н3 = {водитель относится к 3 классу}. Р(Н1) = 0,3; Р(Н2) = 0,5; Р(Н3) = 0,2;

Р(А/Н1) = 0,01; Р(А/Н2) = 0,02; Р(А/Н3) = 0,08;

P( A) = 0,3× 0,01+ 0,5× 0,02 + 0,2× 0,08 = 0,029 .

По формуле Байеса пересчитаем вероятности гипотез, после того, как событие А произошло:

P(H1 \| A) =	0,3× 0,01	» 0,1035 ;
		0,029
P(H 2	\| A) =	0,5× 0,02	» 0,3448 ;
		0,029
P(H3	\| A) =	0,2× 0,08	» 0,5517 .
		0,029

6. Формула Бернулли.

Рассматривается последовательность независимых испытаний, в каждом из которых вероятность наступления события А одинакова и равна р (условно это событие

рассматривается как успех, а его ненаступления ( A ) как неудача, причем p( A) = 1— p = q ).

Вероятность того, что в n испытаниях успех наступит ровно m раз, обозначим через

Pn(m).

Имеет место формула Бернулли:

Pn (m) = Cnm p m q n− m .

Задача 1.

Что вероятнее выиграть у равносильного противника а) три партии из четырех или пять партий из восьми? б) не менее трех партий из четырех или не менее пяти партий из восьми?

Решение.

Так как противники равносильные, то вероятности выигрыша и проигрыша каждой партии одинаковы и равны p = q = ½.

а) Найдем вероятность выигрыша трех партий из четырех:

P (3) = C 3

1 ö

3 ×

æ 1

ö 1

= 1 .

2 ø

è 2

Аналогично, P (5) =

C 5

ö 5

ö 3

Так как

, то вероятнее выиграть три партии из четырех.

б) Вероятность выиграть не менее 3-хпартий их четырех (обозначим ее R4 (3) ). R4 (3) = P4 (3) + P4 (4) = 14 + 161 = 165 ;

Вероятность выиграть не менее пяти партий из восьми ( R8 (5) ):

R8 (5) = P8 (5) + P8 (6) + P8 (7) + P8 (8) = 25693 .

Так как 25693 > 165 , то вероятнее выиграть не менее пяти партий из восьми.

Задача 2.

Всхожесть семян ржи составляет 90%. Чему равна вероятность того, что из семи посеянных семян взойдут пять?

Решение.

Вероятность всхожести отдельно взятого семени р=0,9; q=1-0,9=0,1. По формуле Бернулли:

P7 (5) = C75 p5 q 2 = C75 × (0,9)5 × (0,1)2 = 0,124 .

Таким образом, в среднем в 124 случаях из 1000 из 7 посеянных семян взойдут 5.

7. Дискретные и непрерывные случайные величины.

Величина, которая в зависимости от случай принимает различные числовые значения, называется случайной. Обозначаются они буквами Х, У и т.п.

Вероятность того, что случайная величина Х примет значение, меньшее х, называется функцией распределения случайной величины Х:

F(x)=P(X<x).

Основные свойства функции распределения: 1. Если a<b, то P(a ≤ X < b) = F(b) − F(a) .

2.Функция распределения – неубывающая функция.

3.Функция распределения непрерывна слева, то есть

			lim F( x) = F(a) .
			x→ a−	0
4.	lim F( x) = 1	;	lim F( x) = 0.
	x→ + ∞		x→ − ∞

7.1. Дискретная случайная величина.

Случайная величина называется дискретной, если ее значения можно перенумеровать.

Функция распределения дискретной случайной величины определяется посредством

равенства: F( x) = å pi , где суммирование распространяется на все индексы, для которых

xi<x.

Дискретная случайная величина может быть задана: 1) рядом распределения, 2) многоугольником распределения, 3) функцией распределения.

Рядом распределения называется совокупность всех частных значений, которые принимает случайная величина xi, и соответствующих им вероятностей pi = P{X = xi } . Ряд распределения обычно задается в виде таблицы:

Х		х1	x2	…	xn	…
Р		Р1	р2	…	pn	…
å	pi = 1.
i
Многоугольником распределения называется графическое изображение ряда.
Откладываются точки Ai ( xi , pi )	и соединяются ломанной.

Напоминаем схему решения задач на построение законов распределения.

1)Необходимо обозначить и описать случайную величину, о которой идет речь в задаче.

2)Описать множество ее возможных значений xi.

3)Рассмотреть каждое из событий {X=xi}, i=1,2,…, n.

4)Вычислить вероятность каждого из событий {X=xi} с помощью основных теорем и формул.

5) Проверить правильность составленного распределения с помощью равенства

ån pi = 1. i= 1

Задача 1.

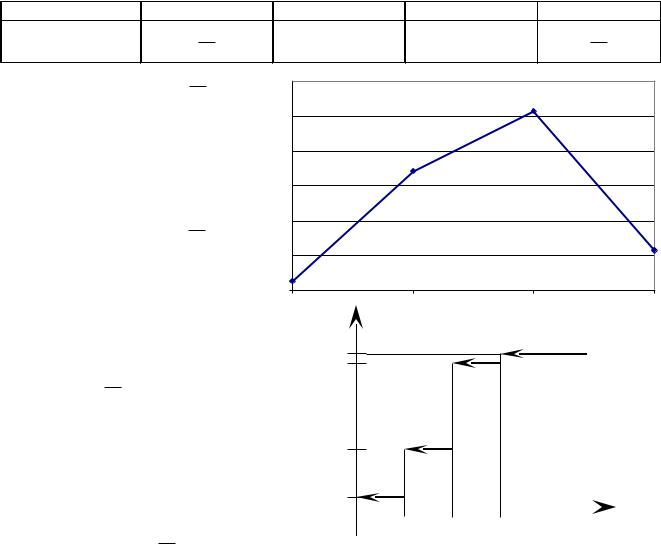
В урне 7 шаров, из которых 4 белых, а остальные черные. Из урны наудачу извлекаются 3 шара. Х – число извлеченных белых шаров. Найти а) закон распределения;

б) построить многоугольник распределения; в) найти и F(x); г)Найти вероятность

события X ³ 2 .

Решение.

Возможные значения случайной величины Х: 0, 1, 2, 3. Заполняем таблицу:

Х						0		1			2	3
Р						1		12			18	4
		C40 × C33			35		35			35	35
P{X = 0} =		=	1	,		3/5
C73		35		1/2				18/35
P{X = 1} =	C41 × C32			12
=	,
C73	35		2/5
P{X = 2} =	C42 × C31		=	18	,	P	3/10		12/35
C73		35
P{X = 3} =	C43 × C30		=	4			1/5
C 3		35 .						4/35
		7						1/10

									1/35
									0
									0	1		2	3
Найдем F(x).							F(x)			X
						1
ì	0, x £	0;
ï	1	,0 <	x £	1;				31/35
ï	35
ï
F( x) = íï	13	,1 < x £ 2;
ï	35								13/35
ï	31	,2 <	x £		3;
ï	35
ï	1, x >	3.						1/35
î
P{ X ³ 2} =	18 +	4			22 .		0	1	2	3	x
	=
		35	35		35

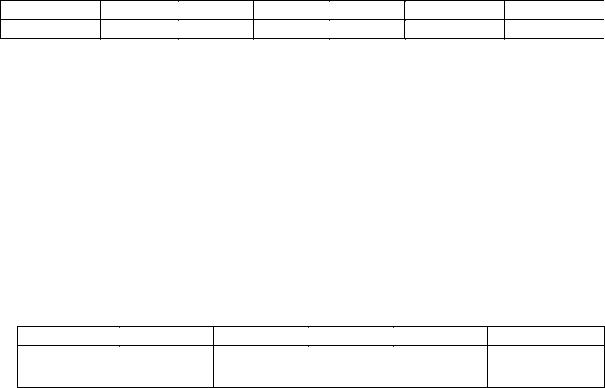
Задача 2.

Пусть ведется стрельба по цели до первого попадания с конечным запасом «k». Пусть Х – число израсходованных патронов до первого попадания. Составить закон распределения случайной величины Х.

Решение.

X		1	2	3	…	k-1	k
P		p	qp	q2p		qk-2p	qk-1p+qk
P{ X = 1} =	p;
P{ X = 2} = q × p;
P{ X = 3} = q2 × p;
…
P{ X = k — 1} = qk − 2 × p.
Событие { X = k}	означает, что израсходован весь запас патронов.

P{ X = k} = qk − 1 × p + q k .

Задача 3.

Имеется 5 ключей, из которых только один подходит к замку. Найти закон распределения случайной величины Х – числа проб при открывании замка, если испробованный ключ в следующих опробываниях не участвует.

Решение.

Х					1					2	3	4	5
Р					1					1	1	1	1
					5					5	5	5	5
P{ X = 1} =	1	;
	5
P{ X = 2} =	4	×	1	= 1	;
	5		4		5
P{ X = 3} =	4	×	3	×	1	=	1 ;
	5		4		3		5
P{ X = 4} =	4	×	3	×	2	×	1	=	1	;
	5		4		3		2		5
P{ X = 5} =	4	×	3	×	2	×	1	×1 =	1 .
	5		4		3		2			5

7.2. Непрерывная случайная величина.

Непрерывной случайной величиной называется такая величина, которая может принимать любые числовые значения из некоторого интервала (конечного и бесконечного). Задать ее можно с помощью функции распределения F(x) или плотности распределения f(x) (дифференциальной функции распределения). Дифференциальной

функцией распределения f(x) называется функция	f ( x) = lim	P( x <	X < x + x)	.

	x→ 0	D x

График функции f(x) называется кривой распределения.

Свойства дифференциальной функции распределения.

1. f ( x) ³ 0 для любого х.

2. P(α < X < β ) = ò f ( x)dx (см. рис.).

f(x)

				x

	+ò∞	α	β

3.	f ( x)dx = 1.

−∞

4.Связь между дифференциальной и интегральной функциями распределения:

F( x) = òx f (t)dt ,

− ∞

F ′( x) = f ( x) , если в точке х функция f(x) непрерывна.

Пример непрерывного распределения.

Равномерное распределение.

Непрерывная случайная величина Х имеет равномерное распределение на отрезке [a, b], если на этом отрезке плотность вероятности случайной величины постоянна, то есть

ì	0, x <	a;
f ( x) = íï c, a £ x £ b;
ï	0, x >	b.
î

Найдем параметр с. Так как +ò∞ f ( x)dx = 1, то имеем:

	− ∞
òa 0× dx + òb c × dx +	+ò∞ 0× dx = 1;
− ∞	a	b

Следовательно, c = Таким образом,

с(b-a)=1,

1 . b — a

ì		0, x
f ( x) = íï	1		, a
	a
ï b —
î		0, x

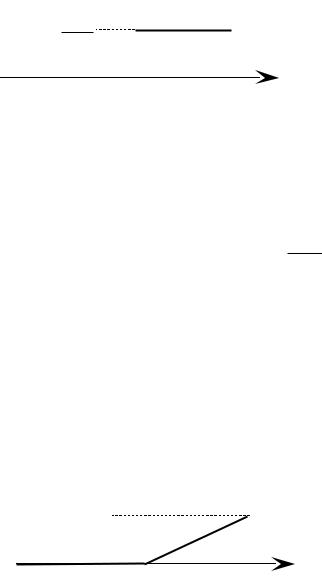
Построим график f(x).

f(x)

b − a

		a	b	x
Найдем функцию распределения F(x):

F( x) = òx f ( x)dx .

− ∞

Если x<a, то F( x)

òx

0 × dx =

0 .

− ∞

Если a £ x £ b , то F( x) = ò 0 × dx +

× dx =

b —

b — a

Если x>b, то F( x)

− ∞

0× dx +

× dx +

0× dx = 1.

b —

Таким образом,

− ∞

0, x <

F( x) = íï

x — a

, a £ x £ b;

ï b —

1, x >

График F(x) представим на рисунке:

=x — a . b — a

F(x)

		1		x

		a	b
Задача 1.	f ( x) = íì	0, x < 0;
Дана функция
	î	Cxe− x , x ³ 0.

При каком С она является плотностью вероятности?

Решение.

Во-первых, f ( x) ³ 0 , если f(x) – плотность вероятности, то есть C ³ 0 . Во-вторых, +ò∞ f ( x)dx = 1.

− ∞

+ ∞

× dx +

Cxe− x dx = C

xe− x dx = C lim

—

— e− A + 1ö

C = 1

− ∞

→ ∞

Ответ: С=1.

8. Числовые характеристики случайной величины.

Пусть Х – случайная дискретная величина, закон распределения которой имеет вид:

X	x1	x2	…	xk	…	xn
P	p1	p2	…	pk	…	pn
Математическим	ожиданием	МХ случайной	величины	Х	называется сумма

произведений значений случайной величины на вероятности, с которыми она принимает эти значения:

MX = ån xi pi .

i= 1

Математическим ожиданием непрерывной случайной величины с плотностью f(x) называется

MX = +ò∞ x × f ( x) × dx ,

− ∞

при условии, что интеграл сходится.

Свойства математического ожидания.

1.M[C]=C, где С – постоянная.

2.M[CX]=CM[X], где С – постоянная.

3.M[X1+X2+…+Xn]=M[X1]+M[X2]+…+M[Xn].

4.Если — независимы, то M[X1×X2×…×Xn]=M[X1] ×M[X2] ×…×M[Xn]. Дисперсией случайной величины Х называется число DX

DX=M[(X—MX)2].

Число σ ( x) = DX называется средним квадратическим отклонением случайной

величины Х.

Справедлива формула

DX=M[X2]-(M[X])2 (*), Этой формулой удобно пользоваться на практике.

Формула нахождения дисперсии для дискретной случайной величины

DX = å (xi — MX )2 pi ,

или с учетом формулы (*):

DX = å xi2 pi — (MX ) 2 .

Формула нахождения дисперсии непрерывной случайной величины:

DX = +ò∞ ( x — MX ) 2 f ( x) × dx , или

− ∞

DX = +ò∞ x 2 f ( x) × dx — (MX ) 2 .

− ∞

Свойства дисперсии.

1.D[C]=0, где С – постоянная.

2.D[CX]=C2D[X], где С – постоянная.

3.D[X ± Y]=D[X] + D[Y], где X, Y – независимые случайные величины.

Задача 1.

Случайная величина Х задана плотностью f(x):

													ì	0, x £ 0;
												f ( x) = íï	2x,0 < x < 1;
													ï	0, x ³ 1.
													î
Найти MX, DX, σX.
Решение.													1
MX =	+ò∞ x × f ( x) × dx = ò1	x × 2x × dx =	2x3		=	2 ,

	− ∞								0		3		0	3

DX = M [X 2 ]— (M [X ])2 ,
M [X 2 ] = ò1 x2 × 2x × dx =	x4		1	=	1	,

2			2
	0									0

DX =	1 —	4	=	9 − 8 =		1	,
9	18
	2			18
σ X =		1		=			1	.
18
3	2

Задача 2.

Пусть задан закон распределения некоторой случайной величины Х:

Х		2	4
Р		0,6	0,4
Найти МХ и DX.
Решение.
MX = å xi	pi = 2× 0,6 + 4× 0,4 = 2,8.
i

DX = M [X 2 ]— (M [X ])2

Напишем закон распределения случайной величины Х2:

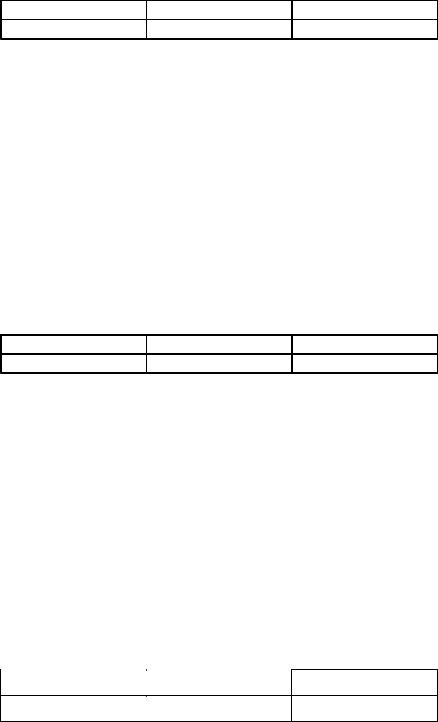
М[X2]=4×0,6+16×0,4=8,8; DX=8,8-(2,8)2=0,96.

Задача 3.

Согласно таблицам смертности, вероятность того, что 25-летний человек проживет еще один год равна 0,992; а вероятность того, что он умрет в течение года равна 0,008. Страховая компания предлагает застраховать жизнь на 10000 рублей. Какова должна быть величина годового взноса, чтобы подобная страховка не была для страховых органов убыточной?

Решение.

Пусть Х – случайная величина, равная выплате застрахованному лицу страховой суммы (за вычетом страхового взноса а). Тогда закон распределения случайной величины Х будет таким:

Х	а-10000	а
Р	0,008	0,992

х1=а-10000, если застрахованный умрет и х2=а, если застрахованный проживет еще

год.

МХ=(а-10000)×0,008+а×0,992=(а-80).

Чтобы страховые органы в среднем не терпели убытка, необходимо, чтобы МХ³0, следовательно, а³80 рублей.

Задача 4

Дискретная случайная величина X может принимать только два значения x1 и x2 , причем x1 < x2 . Известна вероятность p1 = P{ X = x1} = 0,1, MX = 3,9, DX = 0,09 . Написать закон распределения дискретной случайной величины.

Решение.

Составим таблицу: в первом ряду возможные значения случайной величины, во втором – вероятности, с которыми она эти значения принимает:

Х	x1	x2
Р	p1 = 0,1	p
		2
Т.к. p1 + p2 = 1, то	p2 = 1− 0,1 = 0,9 .

Запишем MX :

MX = x1 Ч0,1+ x2 Ч0,9 = 3,9 . Найдем DX :

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Преподаватель который помогает студентам и школьникам в учёбе.

Компания по страхованию автомобилей разделяет водителей по трем классам риска: класс 𝐴 (мало рискует), класс 𝐵 (рискует средне), класс

		Высшая математика
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №16173
		Прошла проверку преподавателем МГУ
		245 руб.

Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл!

Закажите у меня новую работу, просто написав мне в чат!

Описание заказа и 38% решения ( + фото):

Компания по страхованию автомобилей разделяет водителей по трем классам риска: класс 𝐴 (мало рискует), класс 𝐵 (рискует средне), класс 𝐶 (рискует сильно). Компания предполагает, что из всех водителей, застрахованных у нее, 30% принадлежат классу 𝐴, 50% – классу 𝐵, 20% – классу 𝐶. Вероятность того, что в течение года водитель класса 𝐴 попадет хотя бы в одну автокатастрофу, равна 0,01, для водителя класса 𝐵 эта вероятность равна 0,03, а для водителя класса 𝐶 – 0,1. Мистер Джонс страхует свою машину у этой компании и в течение года попадает в автокатастрофу. Какова вероятность того, что он относится к классу 𝐴?

Решение

Основное событие 𝐴 – водитель страхует машину и попадает в аварию. Гипотезы: 𝐻1 − машину страховал водитель класса 𝐴; 𝐻2 − машину страховал водитель класса 𝐵 𝐻3 − машину страховал водитель класса 𝐶. Вероятности гипотез (по условию): Условные вероятности (по условию): Вероятность события 𝐴 по формуле полной вероятности равна: Вероятность того, что попавший в аварию водитель относится к классу 𝐴, по формуле Байеса:

Похожие готовые решения по высшей математике:

Страховая компания разделяет застрахованных клиентов по классам риска: I – малый риск, II – средний, III – большой риск
Стрелок производит 3 выстрела. Вероятности попадания при первом, втором и третьем выстрелах соответственно равны 0,7; 0,8; 0,9. Найти вероятность
В эпоху мезолита (среднего каменного века) для того, чтобы убить зайца, было достаточно двух попаданий из лука
Производится два выстрела по цели. Вероятность попадания при первом выстреле 0,2; при втором – 0,6. Вероятность разрушения цели
Агентство по страхованию автомобилей разделяет водителей по трем классам: №1 (мало рискует), № 2 (рискует средне), № 3 (рискует сильно). Агентство
Агентство по страхованию автомобилей разделяет водителей по трем классам? I-класс – мало рискует, II-класс – средне рискует, III-класс – сильно рискует
Страховая компания разделяет застрахованных по классам риска: малый риск, средний риск, большой риск
Страховая компания продала 100 страховых полисов, страховая сумма по которым выплачивается в случае пожара, 350 страховых полисов

Отдел технического контроля проверяет изделия на стандартность. Вероятность, что изделие стандартное, равна 0,8
В магазин поступают телевизоры четырех заводов. Вероятность того, что в течение года телевизор
Страховая компания разделяет застрахованных клиентов по классам риска: I – малый риск, II – средний, III – большой риск
Вероятность возникновения опасной перегрузки в каждом из трех независимых опытов

Источник

Компания по страхованию автомобилей разделяет водителей по трём классам: класс А (мало рискует), класс В (рискует средне), класс С (рискует сильно)

Компания по страхованию автомобилей разделяет водителей по трём классам: класс А (мало рискует), класс В (рискует средне), класс С (рискует сильно). Компания предполагает, что из всех водителей, застрахованных у неё, 30% принадлежат классу А, 50% — классу В, 20% — классу С. Вероятность того, что в течение года водитель класса А попадёт хотя бы в одну автокатастрофу, равна 0,01; для водителя класса В эта вероятность равна 0,03, а для водителя класса С — 0,1. Мистер Джонс страхует свою машину у этой компании и в течение года попадает в автокатастрофу. Какова вероятность того, что он относится к классу А?

Просмотров: 1475 | Добавил: (24.07.2018) (Изменено: 24.07.2018)

Всего ответов: 1
Обсуждение вопроса: Всего ответов: 1 Порядок вывода комментариев: 0 shurik 24.07.2018 оставил(а) комментарий:

Источник

Готовое решение: Заказ №8391

Тип работы: Задача

Статус: Выполнен (Зачтена преподавателем ВУЗа)

Предмет: Теория вероятности

Дата выполнения: 16.09.2020

Цена: 226 руб.

Чтобы получить решение, напишите мне в WhatsApp, оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным, не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу, я смогу выполнить её в срок 1-3 дня!

Описание и исходные данные задания, 50% решения + фотография:

Агентство по страхованию автомобилей разделяет водителей по 3 классам: класс H₁ (мало рискует), класс H₂ (рискует средне), класс H₃ (рискует сильно). Агентство предполагает, что из всех водителей, застраховавших автомобили, 30 % принадлежат к классу H₁, 50 % – к классу H₂ и 20 % – к классу H₃. Вероятность того, что в течение года водитель класса H₁ попадёт в аварию, равна 0,01, для водителей класса H₂ эта вероятность равна 0,02, а для водителя класса H₃ – 0,08. Водитель страхует свою машину и в течение года попадает в аварию. Какова вероятность того, что он относится к классу H₁?

Решение.

Пусть событие A – случайно выбранный водитель, застраховавший свою машину, в течение года попадёт в аварию.

Выдвинем следующие гипотезы:

H₁ – водитель рискует мало (относится к классу H₁);

H₂ – водитель рискует средне (относится к классу H₂);

H₃ – водитель рискует сильно (относится к классу H₃).

По статистическому определению вероятности, вероятности гипотез равны:

Условные вероятности события A известны:

Агентство предполагает, что из всех водителей, застраховавших автомобили, 30 % принадлежат к классу H1, 50 % – к классу H2 и 20 % – к классу H3. Вероятность того, что в течение года водитель класса H1 попадёт хотя бы в одну аварию, равна 0,01, для водителей класса H2 эта вероятность равна 0,02, а для водителя класса H3 – 0,08. Водитель A страхует свою машину и в течение года попадает в аварию. Какова вероятность того, что он относится к классу H1? К классу H2? К классу H3?
Среди клиентов страховой компании 50 % относится к классу малого риска, 30 % – к классу среднего риска и 20 % – к классу большого риска. Вероятность необходимости выплачивать страховое вознаграждение для класса малого риска равна 0,01, среднего – 0,03, большого – 0,08. Какова вероятность того, что:
Вероятность того, что изделие, произведённое первым изготовителем, имеет скрытый дефект, равна p1, для второго и третьего изготовителей эти вероятности равны, соответственно p2 и p3. m = 65, n = 15, p1 = 0,03, p2 = 0,05, p3 = 0,04.
На трёх дочерей – Анну, Бетти и Шарлотту – в семье возложена обязанность мыть посуду. Поскольку Анна старшая, она выполняет 40 % всей работы. Остальные 60 % Бетти и Шарлотта делят пополам. Когда Анна моет посуду, вероятность для неё разбить хотя бы одну тарелку равна 0,02; для Бетти – 0,03; для Шарлотты – 0,02. Родители не знают, кто мыл тарелки вечером, но они слышали звон разбитой посуды. Какова вероятность того, что посуду мыла Анна?

Источник

Агентство по страхованию автомобилей разделяет водителей по трем классам : Р 1 класс – практически не рискует, Р2 класс – мало рискует, Р3 класс – всегда рискует.

Анализ застрахованных водителей предыдущих периодов показал, что 24% принадлежат к классу Р1, 48% — к классу Р2 и 28% — к классу З3.

Вероятность того, что в течение года водитель класса Р1 попадет хотя бы в одну аварию, равна 0, 01 ; для водителя класса Р2 вероятность равна 0, 015 ; для водителя Р3 класса – 0, 024.

Какова вероятность того, что водитель ни разу не попавший в аварию из класса Р1?

Вы открыли страницу вопроса Агентство по страхованию автомобилей разделяет водителей по трем классам : Р 1 класс – практически не рискует, Р2 класс – мало рискует, Р3 класс – всегда рискует?. Он относится к категории
Математика. Уровень сложности вопроса – для учащихся 10 — 11 классов.
Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие
ответы по интересующей теме. Чтобы получить наиболее развернутый ответ,
можно просмотреть другие, похожие вопросы в категории Математика,
воспользовавшись поисковой системой, или ознакомиться с ответами других
пользователей. Для расширения границ поиска создайте новый вопрос, используя
ключевые слова. Введите его в строку, нажав кнопку вверху.

Источник

С этим файлом связано 1 файл(ов). Среди них: Конспект урока (КСП) по русскому языку Имя прилагательное 2 клас.
Показать все связанные файлы

Подборка по базе: Самостоятельная работа по теме «Государственная политика в сфере, ЧАСТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ.docx, краевое государственное бюджетное.docx, ……..готова Государственное управление в сфере внутренних де, ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИ, Негосударственное образовательное учреждение.docx, Государственное бюджетное профессиональное образовательное учреж, М. Порядок оформления возникновения, приостановления и прекращен, КОМИТЕТ ПО ДЕЛАМ ОБРАЗОВАНИЯ ГОРОДА ЧЕЛЯБИНСКА МУНИЦИПАЛЬНОЕ АВТ, Негосударственное образовательное учреждение.docx

Задание 1/4
Для ответа на вопрос отметьте нужные варианты ответа. При обсуждении информации о музее ребята высказали несколько утверждений.
Отметьте все верные варианты ответа.

В музее меньше 900 игрушек.

В музее есть игрушки, сделанные в 2021 г.

На трёх мастер-классах предлагается расписывать готовые игрушки.

В музее экспонируются игрушки, изготовленные в IX веке.

Мастер-класс займет меньше 3–4 часов.
Решение:
Из текста следуют 3 верных утверждения:
В музее меньше 900 игрушек.
На трёх мастер-классах предлагается расписывать готовые игрушки.
Мастер-класс займет меньше 3–4 часов.
Формы работы: индивидуальная с проверкой.
Задание 2/4
Прочитайте текст «Экскурсия в музей» и рассмотрите расписание электричек в таблице 5.

79
Таблица 5. Расписание электричек
Отправление из
Москвы
с Ярославского
вокзала
Прибытие
в Сергиев
Посад
Режим
движения
Цена одного
билета (руб.)
09:04 10:35 ежедневно
208 09:20 10:24 по воскресеньям
208 09:35 10:51 ежедневно
208 09:40 11:12 ежедневно
208
Для ответа на вопрос отметьте нужный вариант ответа.
Всех интересовало, сколько времени занимает поездка на электричке от Москвы до Сергиева Посада. Какая из электричек преодолевает расстояние до
Сергиева Посада быстрее всего?
Отметьте один верный вариант ответа.

09:04

09:20

09:35

09:40
Решение:
10 ч 35 мин – 09 ч 04 мин = 1 ч 31 мин
10 ч 24 мин – 09 ч 20 мин = 1 ч 04 мин – самое маленькое время
10 ч 51 мин – 09 ч 35 мин = 1ч 16 мин
11 ч 12 мин – 09 ч 40 мин = 1ч 32 мин
Ответ: 09:20
Формы работы: групповая с распределением работы и взаимопроверкой.

80
Задание 3/4
Прочитайте текст «Экскурсия в музей» и рассмотрите расписание
электричек в таблице 5. Запишите свой ответ на вопрос.
Ребята узнали, что от железнодорожной станции Сергиев Посад до музея можно дойти за 12–15 минут. Укажите время отправления из Москвы всех электричек (см. таблицу 5), на которых могут доехать ребята, чтобы успеть на экскурсию.
Запишите свой ответ.
Решение:
10 ч 35 мин + 15 мин = 10 ч 50 мин – успеют
10 ч 24 мин + 15 мин = 10 ч 39 мин – успеют
10 ч 51 мин +15 мин = 11 ч 06 мин – не успеют
Ответ: 09:04 и 09:20
Формы работы: групповая с распределением работы и взаимопроверкой.
Задание 4/4
Прочитайте текст «Экскурсия в музей». Для ответа на вопрос отметьте
нужный вариант ответа, а затем объясните свой ответ.
Ирина Петровна – классный руководитель – заказала экскурсию в музей на 11 часов. Ребята планировали побыть на экскурсии, которая занимает около 1 часа, затем посетить один мастер-класс, после чего пообедать в кафе рядом с музеем примерно за 1 час 30 минут.
Успеют ли ребята выполнить все намеченные дела до 15 часов?
Объясните свой ответ.
Решение:
11 ч + 1 ч 40 мин + 1 ч 30 мин = 14 ч 10 мин < 15 ч
Ответ: успеют.
Формы работы: индивидуальная с проверкой.
Задание 5. Московский метрополитен (7 класс) [5]
В кассе московского метрополитена продают билеты на различное число поездок (таблица 6).

81
Таблица 6
Число поездок
1 2
20 40 60
Стоимость билета, р.
55 110 747 1494 1765
Задание 1/2
Для проведения рекламной кампании с целью увеличения покупок билетов на
40 поездок рекламной службе метрополитена необходимо сообщить пассажирам, сколько рублей можно сэкономить, покупая билет на 40 поездок (при условии использования всех поездок), по сравнению с покупкой одноразовых билетов?
Запишите ответ и приведите соответствующее решение.
Решение:
1) 55 · 40 = 2200 (руб.) – стоимость одноразовых билетов на 40 поездок (при условии использования всех поездок).
2) 2200 – 1494 = 706 (руб.) – можно сэкономить, покупая билет на 40 поездок
(при условии использования всех поездок), по сравнению с покупкой одноразовых билетов.
Ответ: 706.
Формы работы: групповая с коллективным обсуждением проблемы.
Задание 2/2
Билеты на одну и на две поездки действуют 5 дней с момента продажи (включая день продажи). Билеты на 20, 40, 60 поездок действуют 90 дней с момента продажи.
Не всегда удаётся, купив билет на определённое число поездок, совершить все поездки за отведённое количество дней. Например, пассажир, который рассчитывает на то, что он будет ездить на работу 5 дней в неделю, может надолго заболеть или неожиданно уехать в командировку.
Какое наименьшее число поездок надо совершить, чтобы стоимость билета на
40 поездок не превысила стоимости одноразовых билетов?
Решение:
1494 : 55 = 27 (ост. 9)

82
Ответ: 28.
Формы работы: работа в парах с общей проверкой и обсуждением способа округления.
Задание 6. Кулинарный колледж (8 класс) [5]
Наташа и Оля учатся в кулинарном колледже. Они изучают технологии приготовления различных блюд. На занятиях по теме «Каши и блюда из круп» при вычислении массы готового продукта обучающиеся считают, что:
1 порция – это 200 г готовой каши; из 1 кг пшённой крупы получается 4 кг готовой каши; для приготовления 1 кг готовой каши пшённой необходимо 0,8 л жидкости, из которой 40% составляет вода и 60% – молоко.
Задание 1/2
На практическом занятии Наташа и Оля получили задание определить количество порций каши пшённой, которое можно приготовить из 3 кг пшена.
Сделайте расчёты и приведите ответ.
Решение:
1) 3 4 = 12 кг готовой каши получается из 3 кг пшённой крупы.
2) 12 : 0,2 = 60 порций.
Ответ: 60 порций.
Формы работы: индивидуальная.
Задание 2/2
Наташа и Оля должны рассчитать, сколько литров воды и сколько литров молока необходимо для приготовления 1 кг каши пшённой.
Сделайте расчёты и приведите ответ.
Решение:
1) 0,8 · 0,4 = 0,32 л воды.
2) 0,8 · 0,6 = 0,48 л или 0,8 – 0,32 = 0,48 л молока.
Ответ: 0,32 л воды и 0,48 л молока.
Формы работы: парная.

83
Кейс № 8. Учебный раздел «Случайные события» (8 класс)
Выбор потребителя
Методическая проблема
Формирование компетенции математической грамотности «распознавать математические объекты и закономерности в реальных жизненных ситуациях» в рамках изучения раздела «Случайные события».
Анализ методической проблемы
Выделение математического содержания в контексте реальной ситуации является одной из компетенций математической грамотности. «Умение распознавать проявления математических понятий, объектов и закономерностей в реальных жизненных ситуациях и при изучении других учебных предметов, проявления зависимостей и закономерностей» входит в приоритетные цели обучения математике в 5–9 классах, представленные в Примерной основной образовательной программе основного общего образования (протокол от 18 марта 2022 г. № 1/22) [9].
Однако в существующих УМК в большей степени присутствуют задания, ориентированные преимущественно на освоение математического аппарата, и практически отсутствуют задания, которые позволяли бы целенаправленно формировать «умение распознавать проявления математических понятий, объектов и закономерностей в реальных жизненных ситуациях».
В федеральном государственном образовательном стандарте основного общего образования, утверждённом приказом Министерства просвещения Российской
Федерации от 31 мая 2021 г. № 287, отмечается важность прикладного характера математики как описательного языка науки и техники, средства моделирования процессов и явлений, в том числе из повседневной жизни [11]. Включение теории вероятностей и математической статистики в школьный курс математики отражает возрастание их значимости при получении, анализе и обработке информации и последующего принятия решений в различных ситуациях с неожиданными исходами.
Таким образом, раздел «Случайные события» может стать предметной основой для

84 формирования «умения распознавать проявления математических понятий, объектов и закономерностей в реальных жизненных ситуациях и при изучении других учебных предметов, проявления зависимостей и закономерностей».
Цель
Раскрыть способы формирования компетенции математической грамотности
«распознавать математические объекты и закономерности в реальных жизненных ситуациях» в рамках изучения раздела «Случайные события».
Задачи
1. Выделить характеристики деятельности обучающихся в основном содержании темы «Случайные события».
2. Разработать систему типовых заданий на формирование компетенции
«распознавать математические объекты и закономерности в реальных жизненных ситуациях».
3. Описать методические приемы формирования компетенции «распознавать математические объекты и закономерности в реальных жизненных ситуациях» в рамках изучения темы «Случайные события».
Способы решения методической проблемы
В таблице 1 представлены характеристики деятельности обучающихся в основном содержании темы «Случайные события».
Таблица 1. Характеристики деятельности обучающихся в основном содержании
темы «Случайные события»
Основное содержание
Характеристики деятельности обучающихся
Противоположное событие.
Диаграмма
Эйлера. Объединение и пересечение событий.
Осваивать понятия: взаимно противоположные события, операции над событиями, объединение и пересечение событий, диаграмма Эйлера (Эйлера–
Венна), совместные и несовместные события.
Несовместные события.
Формула сложения
Изучать теоремы о вероятности объединения двух событий (формулы сложения вероятностей).

85
Основное содержание
Характеристики деятельности обучающихся
вероятностей. Правило умножения вероятностей. Условная вероятность.
Независимые события.
Представление случайного эксперимента в виде дерева
Решать задачи, в том числе текстовые задачи на определение вероятностей объединения и пересечения событий, с помощью числовой прямой, диаграмм Эйлера, формулы сложения вероятностей.
Осваивать
понятия: правило умножения вероятностей, условная вероятность, независимые события дерево случайного опыта.
Изучать свойства (определения) независимых событий.
Решать задачи на определение и использование независимых событий.
Формирование компетенции математической грамотности «распознавать математические объекты и закономерности в реальных жизненных ситуациях» в рамках темы «Случайные события» следует поэтапно.
На первом этапе необходимо, чтобы обучающиеся научились выделять понятийный аппарат теории вероятностей в описании реальной ситуации. Для этого можно предложить следующие задания.
Задание 1
Замените слова в описании реальной ситуации на термины теории вероятностей.
1) В танцевальном кружке занимаются 15 девочек и 10 мальчиков. На конкурс необходимо отобрать 3 пары детей. Оцените возможность попасть на конкурс для девочки и для мальчика.
Ответ: «возможность» следует заменить на «вероятность»
2) Магазин проводит акцию. Покупатель, купивший каждую сотую коробку конфет марки «N», выигрывает 500 рублей. Покупатель A выиграл 500 рублей. Как можно охарактеризовать покупку сотой коробки и девяноста девяти предыдущих?
Ответ: как противоположные события, как несовместные события.

86 3) При бросании игрального кубика могут выпасть числа от 1 до 6. Как можно назвать все шесть случаев?
Ответ: полная группа событий.
Формы работы: коллективное обсуждение.
На следующем этапе следует предложить обучающимся описать ситуацию как математическую задачу, определить тип задачи и необходимый для решения математический аппарат.
Задание 2
Опишите реальную ситуацию в терминах математической задачи и
приведите необходимый математический аппарат для ее решения.
Петр Иванович решил заказать товар в интернет-магазине. Он изучил отзывы покупателей о работе двух интернет-магазинов, которые представлены в таблице 2.
Таблица 2. Отзывы покупателей о работе двух интернет-магазинов
Магазин 1
Магазин 2
Всего отзывов – 120
Недовольны качеством товара – 20 чел.
Не вовремя доставлен товар – 12 чел.
Всего отзывов – 150
Недовольны качеством товара – 18 чел.
Не вовремя доставлен товар – 12 чел.
Оцените возможность получить товар не вовремя, если заказать его сразу в двух магазинах.
Решение:
Необходимо вычислить вероятности трех событий, которые составляют полную группу событий:
А – получить товар не вовремя в 1 магазине:
P(A) = 12 : 120 = 0,1
𝐴̅ – получить товар вовремя в 1 магазине
𝑃(𝐴̅) = 1 – 0,1 = 0,9
B – получить товар не вовремя во 2 магазине:

87
P(B) = 12 : 150 = 0,08
𝐵̅ – получить товар вовремя во 2 магазине
𝑃(𝐵̅) = 1 – 0,08 = 0,92
P(AB) = 0,1 · 0,08 = 0,008
Тогда вероятность события E – получить товар не вовремя – будет равна сумме вероятностей:
P(E) = 0,1 · 0,92 + 0,08 · 0,9 + 0,008 = 0,172
Формы работы: коллективное обсуждение решения.
Далее предлагаем аналогичную задачу на самостоятельную работу
Пример задачи
Компания по страхованию автомобилей разделяет водителей по трем классам: класс А (мало рискует), класс В (рискует средне), класс С (рискует сильно).
На диаграмме (Рисунок 1) представлено распределение водителей по классам.
Рисунок 1. Распределение водителей по классам
Вероятность того, что в течение года водитель класса А попадет хотя бы в одну автокатастрофу, равна 0,01; для водителя класса В эта вероятность равна 0,04, а для водителя класса С – 0,1.
К какому классу компания должна отнести Игоря Владимировича, если вероятность, что в течение года он попадет в автокатастрофу, составляет не более 0,1?
Класс А
30%
Класс В
55%
Класс С
15%

88
Решение:
Найдем вероятность того, что наугад выбранный застрахованный водитель в течение года попадет хотя бы в одну автокатастрофу.
𝑃 = 0,3 ∙ 0,01 + 0,55 ∙ 0,04 + 0,15 ∙ 0,1 = 0,04
Найдем
𝑃
𝐴
=
0,003 0,04
≈ 0,075;
𝑃
𝐵
=
0,022 0,04
≈ 0,55;
𝑃
с
=
0,015 0,04
≈ 0,375
Ответ: к классу А.
Формы работы: по парам, в группах по 5–6 человек. Можно использовать один и тот же сюжет и разные данные или разные сюжеты (о работе различных устройств, о бракованных изделиях и др.). После выполнения задания необходимо организовать коллективное обсуждение решения.
Далее обучающимся предлагается составить задачу на использование формулы полной вероятности
Формы работы: индивидуальная.

89
Кейс № 9. Учебный раздел
«Вероятность случайного события» (8 класс)
Благоприятные исходы
Методическая проблема
Формирование компетенции математической грамотности «распознавать математические объекты и закономерности в реальных жизненных ситуациях» в рамках изучения раздела «Вероятность случайного события».
Анализ методической проблемы
Включение в программу школьного курса математики стохастической линии связано c необходимостью формирования у обучающихся умений выдвигать гипотезы, анализировать случайные факторы, оценивать различные варианты развития событий, делать прогнозы и принимать решения в ситуациях неопределённости. Для лучшего понимания сущности рассматриваемых понятий необходимо использование реальных ситуаций в качестве их наглядного представления, что позволяет органично сочетать процесс изучения теории вероятностей и математической статистики с формированием математической грамотности.
Одной из составляющих математической грамотности выступает «умение распознавать проявления математических понятий, объектов и закономерностей в реальных жизненных ситуациях и при изучении других учебных предметов, проявления зависимостей и закономерностей», что зафиксировано в приоритетных целях обучения математике в 5–9 классах, содержащихся в Примерной основной образовательной программе основного общего образования (протокол от 18 марта
2022 г. № 1/22) [9].
В случае с изучением теории вероятностей (раздел «Вероятность случайного события») это предполагает выделение в описании реальной ситуации таких понятий, как случайные, элементарные и равновозможные события, вероятность.

90
Цель
Раскрыть способы формирования компетенции математической грамотности
«распознавать математические объекты и закономерности в реальных жизненных ситуациях» в рамках раздела «Вероятность случайного события».
Задачи
1. Выделить характеристики деятельности обучающихся в основном содержании раздела «Вероятность случайного события».
2. Разработать систему типовых заданий на формирование компетенции
«распознавать математические объекты и закономерности в реальных жизненных ситуациях».
3. Описать методические приемы формирования компетенции «распознавать математические объекты и закономерности в реальных жизненных ситуациях» в рамках изучения раздела «Вероятность случайного события».
Способы решения методической проблемы
В таблице 1 представлены характеристики деятельности обучающихся в основном содержании раздела «Вероятность случайного события».
Таблица 1. Характеристики деятельности обучающихся в основном содержании
раздела «Вероятность случайного события»
Основное содержание

Источник

Компания по страхованию автомобилей разделяет водителей по трем классам риска: класс 𝐴 (мало рискует), класс 𝐵 (рискует средне), класс

Компания по страхованию автомобилей разделяет водителей по трём классам: класс А (мало рискует), класс В (рискует средне), класс С (рискует сильно)

Обсуждение вопроса:

Описание и исходные данные задания, 50% решения + фотография: