![Контрольная работа по ЭММ и ПМ Вариант №7 [28.05.13]](https://studrb.ru/files/works_screen/1/42/99.png)
Тема: Контрольная работа по ЭММ и ПМ Вариант №7
Раздел: Бесплатные рефераты по ЭММ и ПМ
Тип: Контрольная работа | Размер: 1.38M | Скачано: 162 | Добавлен 28.05.13 в 17:45 | Рейтинг: 0 | Еще Контрольные работы
Вуз: Финансовый университет
Оглавление
Задача 2.7. 3
Задача 3.7. 12
Задача 4.7. 21
Задача 5.7. 32
Список литературы.. 36
Задача 2.7
Можно закупить корм видов 1 и 2, при этом стоимость единиц корма вида 1 равна 2 ден. единицам, а вида 2 – 4 ден. единицы. В каждой единице корма 1 содержится одна единица витамина А, две единицы витамина В и нет витамина С, а в каждой единице корма 2 – две единицы витамина А, одна единица В и одна единица С. Животному в сутки необходимо не менее 10 единиц витамина А, 10 единиц витамина В и 4 единицы витамина С. Составить наиболее дешевый рацион питания животного в расчете на сутки.
|
содержание питат. веществ |
норма содержания |
||
|
Витамины |
1 |
2 |
|
|
А |
1 |
2 |
10 |
|
В |
2 |
1 |
10 |
|
С |
0 |
1 |
4 |
|
Стоимость 1 ед. |
2 |
4 |
Таблица 1.
Экономико-математическая модель задачи:
Пусть Х1 – количество корма 1 , X2 – количество корма 2, тогда суммарная стоимость будет равна:
Z=2X1+4X2 → min (1)
Задача 3.7
Компания владеет тремя фабриками F1, F2 и F3, способными произвести еженедельно 50, 25 и 25 тыс. изделий соответственно. По договорам компания поставляет продукцию четырем заказчикам С1, С2, С3 и С4, каждому из которых требуется 15, 20, 20 и 30 тыс. изделий еженедельно. Стоимости производства и транспортировки 1 тыс. изделий с фабрики F1 каждому из заказчиков составляют 13, 17, 17 и 14 ден. единиц соответственно; аналогичные стоимости для фабрики F2 равны 18, 16, 16 и 18 ден. единиц, а для фабрики F3 – 12, 14, 19 и 17 ден. единиц. Определить оптимальный план производства и транспортировки продукции, минимизирующий общие затраты компании.
|
Фабрики |
Затраты на перевозку 1 тыс. изделий к заказчикам |
Запас изделий, тыс |
|||
|
С1 |
С2 |
С3 |
С4 |
||
|
F1 F2 F3 |
13 18 12 |
17 16 14 |
17 16 19 |
14 18 17 |
50 25 25 |
|
Потребности в изделиях, тыс |
15 |
20 |
20 |
30 |
Таблица 2.
Данная задача является транспортной задачей открытого типа, так как запасы продукции у поставщиков (фабрик) больше потребностей в изделиях у заказчиков.
Транспортную задачу открытого типа предварительно необходимо свести к закрытой, для чего вводится фиктивный пункт производства с номером m+1 с объемом производства:
|
Фабрики |
Затраты на перевозку 1 тыс. изделий к заказчикам |
Запас изделий, тыс |
||||
|
С1 |
С2 |
С3 |
С4 |
С5 |
||
|
F1 F2 F3 |
13 18 12 |
17 16 14 |
17 16 19 |
14 18 17 |
0 0 0 |
50 25 25 |
|
Потребности в изделиях, тыс |
15 |
20 |
20 |
30 |
15 |
100 |
Таблица 3.
Экономико-математическая модель задачи:
Переменные: хij(i=1,3; j=1,5) – количество продукции, поставляемой i-ой фабрикой j-у заказчику.
Целевая функция – суммарные транспортные издержки, которые надо минимизировать:
F(X) = 13х11 + 17х12 + 17х13 + 14х14 + 18х21 + 16х22 + 16х23 + 18х24 + 12х31 + 14х32 + 19х33 + 17х34 min
Задача 4.7
В таблице приведены годовые данные о трудоемкости производства 1 т цемента (нормо-смен) (N – последняя цифра зачетной книжки студента):
Таблица 3.
N = 7.
Задание 1. Сгладить временной ряд методом простой скользящей средней, выбрав длину интервала сглаживания m= 3; результаты отразить на графике.
Задание 2. Определить наличие тренда во временном ряду методом Фостера-Стьюарта. Табличные значения статистики Стьюдента tα принять равными при уровне значимости α = 0,05 tα = 2,23, а при α = 0,30 — tα = 1,09; другие необходимые табличные данные приведены в таблице 4,5 учебника на с. 153.
Задание 3. Для исходного временного ряда построить линейную трендовую модель , определив ее параметры на основе метода наименьших квадратов.
Задание 4. Оценить адекватность построенной модели на основе исследования
а) близости математического ожидания остаточной компоненты (ряда остатков) нулю; критические значения t-критерия принять равным тому числу, как указано в задании 2;
б) случайности отклонений остаточной компоненты по критерию пиков (поворотных точек);
расчеты выполнить на основе соотношения (5.9) на стр. 200 учебника;
в) независимости уровней ряда остатков (отсутствие автокорреляции) на основе критерия Дарбина-Уотсона (см. учебник с. 203-204), используя в качестве критических значений d1 = 1,08 и d2 = 1,36; если критерий Дарбина-Уотсона ответа не дает, исследование независимости провести по первому коэффициенту автокорреляции:
г) нормальности закона распределения уровней остаточной компоненты на основе RS-критерия;
в качестве критических значений принять интервал от 2,7 до 3,7 (см. учебник с. 201-202).
Модель является адекватной, если математическое ожидание значений остаточного ряда случайны, независимы и подчинены нормальному закону распределения.
Задание 5. Оценить точность построенной трендовой линейной модели, используя показатели среднего квадратического отклонения от линии тренда (формула 5,17 учебника на с. 210, k = 1) и средней относительной ошибки аппроксимации (формула 5,14 учебника на с. 204).
Задание 6. Построить точечный и интервальный прогноз трудоемкости производства 1 т цемента на два шага вперед (формула 5.18 учебника на с. 210). Результаты моделирования и прогнозирования отразить на графике.
Задача 5.7
В таблице представлены первый (хij) и второй (Yi) квадранты схемы межотраслевого баланса производства и распределения продукции для трехотраслевой экономической системы (N – последняя цифра зачетной книжки студента):
Задание 1. Рассчитать объемы валовой продукции отраслей (формула 6.2 учебника на с. 237).
Задание 2. Рассчитать матрицу коэффициентов прямых затрат А = (aij) (формула 6.4 учебника на с.238).
Задание 3. Найти матрицу коэффициентов полных затрат В = (bij), используя формулу 6.16 учебника на с. 244.
Задание 4. Рассчитать объемы условно чистой продукции отраслей Zij, используя формулу 6.1 учебника на с. 236.
Задание 5. Представить в таблице полную схему межотраслевого баланса (в соответствии с принципиальной схемой МОБ табл. 6.1 учебника на с. 234).
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы
Бесплатная оценка
0
Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).
Чтобы скачать бесплатно Контрольные работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.
Важно! Все представленные Контрольные работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.
Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.
Добавить работу
Если Контрольная работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.
Добавление отзыва к работе
Добавить отзыв могут только зарегистрированные пользователи.
Похожие работы
- Контрольная работа по ЭММ и ПМ Вариант №7
- Контрольная работа по ЭММ и ПМ вариант №7
- Контрольная работа по ЭММ и ПМ Вариант 7
- Контрольная работа по ЭММ и ПМ Вариант №7
- Контрольная работа по ЭММ и ПМ Вариант №7
- Контрольная работа по ЭММ и ПМ Вариант №7
- Контрольная работа по ЭММ и ПМ Вариант №7
- Контрольная работа по ЭММ и ПМ Вариант №7
- Контрольная работа по ЭММ и ПМ Вариант №7
- Контрольная работа по ЭММ и ПМ Вариант №7
- Контрольная работа по ЭММ и ПМ Вариант №7
- Контрольная работа по ЭММ и ПМ Вариант №7
1. Транспортная задача
Компания контролирует три фабрики А1, А2, А3,
способные произвести 50, 25 и 25 тысяч изделий ежедневно.
Она заключила договоры с четырьмя заказчиками В1, В2, В3 и В4,
которым ежедневно требуется 25, 20, 30 и 25 тысяч изделий
соответственно. Стоимости транспортировки 1 тысячи изделий
заказчикам с фабрик следующие:
Определить минимизирующий общую стоимость план
перевозок изделий от фабрик к заказчикам.
2.
Составляем математическую модель задачи:
Компания контролирует три фабрики А1, А2, А3,
способные произвести 50, 25 и 25 тысяч изделий ежедневно.
Она заключила договоры с четырьмя заказчиками В1, В2, В3 и В4,
которым ежедневно требуется 25, 20, 30 и 25 тысяч изделий
соответственно.
Пусть
xij
количество изделий, перевозимых с i-й фабрики
j-му заказчику
B1
A1
A2
A3
x11
x21
x31
B2
x12
x22
x32
B3
B4
x13 x14
x23 x24
x33 x34
3.
Составляем математическую модель задачи:
Компания контролирует три фабрики А1, А2, А3,
способные произвести 50, 25 и 25 тысяч изделий ежедневно.
Она заключила договоры с четырьмя заказчиками В1, В2, В3 и В4,
которым ежедневно требуется 25, 20, 30 и 25 тысяч изделий
соответственно.
Пусть
xij
B1
A1
A2
A3
x11
x21
x31
количество изделий, перевозимых с i-й фабрики
j-му заказчику
B2
x12
x22
x32
B3
B4
x13 x14
x23 x24
x33 x34
4
x
50
x
25
x
25
1j
j 1
4
j 1
4
j 1
2j
3j
4.
Составляем математическую модель задачи:
Компания контролирует три фабрики А1, А2, А3,
способные произвести 50, 25 и 25 тысяч изделий ежедневно.
Она заключила договоры с четырьмя заказчиками В1, В2, В3 и В4,
которым ежедневно требуется 25, 20, 30 и 25 тысяч изделий
соответственно.
xij
Пусть
количество изделий, перевозимых с i-й фабрики
j-му заказчику
B1
A1
A2
A3
3
x11
x21
x31
x
i 1
i1
25
B2
3
B3
x12
x22
x32
x
i 1
i2
20
B4
x13 x14
x23 x24
x33 x34
3
x
i 1
i2
30
4
x
i 1
i2
25
5.
Стоимости транспортировки 1 тысячи изделий
заказчикам с фабрик следующие:
Определить минимизирующий общую стоимость план
перевозок изделий от фабрик к заказчикам.
Пусть
cij
стоимость перевозки с i-й фабрики j-му
потребителю
13 17 17 14
матрица стоимостей
C 18 16 16 18
12 14 19 17
6.
Математическая модель:
Найти матрицу перевозок Х, такую чтобы
3
4
c
i 1 j 1
ij
xij min
3
3
4
3
xi1 25, xi 2 20, xi 2 30, xi 2 25
i 1
i 1
i 1
i 1
4
4
4
x1 j 50, x2 j 25, x3 j 25
j 1
j 1
j 1
x 0
ij
7.
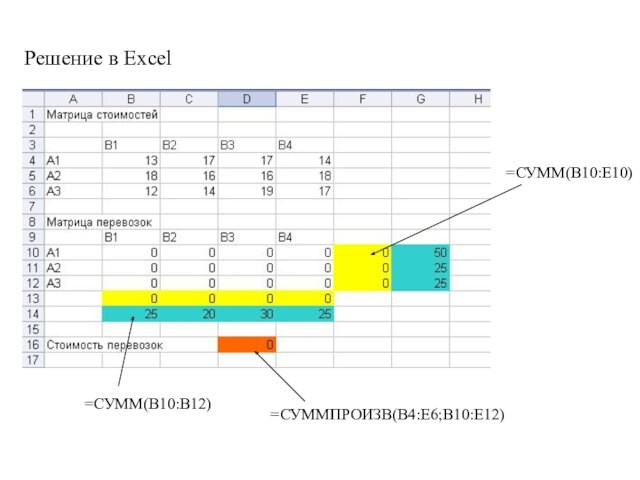
Решение в Excel
=СУММ(B10:E10)
=СУММ(B10:B12)
=СУММПРОИЗВ(B4:E6;B10:E12)
1.
Сталеплавильная компания располагает
тремя заводами M1, M2 и M3, способными
произвести за некоторый промежуток
времени 50, 30 и 20 тыс. т стали соответственно.
Свою продукцию компания поставляет
четырем потребителям C1, C2, C3 и C4, потребности
которых составляют соответственно 24,
15, 25 и 36 тыс. т стали. Стоимости производства
и транспортировки 1 тыс. т стали с
различных заводов различным потребителям
приведены ниже:
-
Потребитель
Завод
M1
M2
M3
C1
10
17
14
C2
12
18
16
C3
19
13
20
C4
15
19
18
Определите
минимальные общую стоимость, объемы
производства на каждом заводе и планы
перевозок.
2.
Фирма ведет работы в различных странах
мира. Ей необходимо перевозить бригады
своих специалистов в разные части света.
Стоимость перевозок в условных единицах
одной бригады самолетами различных
авиакомпаний приведена в таблице:
|
Авиакомпания |
Сидней |
Калькутта |
Бейрут |
Даллас |
Сан-Паулу |
|
С-Эйр |
24 |
16 |
8 |
10 |
14 |
|
Пит |
21 |
15 |
7 |
12 |
16 |
|
Лайнс |
23 |
14 |
7 |
14 |
12 |
Администрация
фирмы решила, что индивидуальные
контракты на перевозку будут заключаться
с владельцами авиалинии С-Эйр, Пит
Эрлайнз и Лайнс Т. в отношении 2:3:2. То
есть из каждых 7 рейсов 2 будут переданы
компании С-Эйр, 3 – компании Пит Эрлайнз
и 2 – для Лайнс Т и уведомила об этом
управляющего транспортными перевозками,
а также известила его о том, что из 70
намеченных на следующий год перевозок
10 – в Сидней, 15 – в Калькутту, 20 – в
Бейрут, 10 – в Даллас и 15 – в Сан-Паулу.
Как
ему следует распределить индивидуальные
контракты на перевозки для минимизации
общей стоимости при условии удовлетворения
запросов администрации фирмы? Какова
минимальная стоимость перевозок,
удовлетворяющих приведенным выше
ограничениям?
3.
Компания владеет двумя фабриками F1 и
F2, производящими электронное оборудование.
Фабрики в течение некоторого периода
выпускает 16 и 14 тыс. изделий соответственно
при нормальных темпах производства.
Компания
снабжает трех потребителей C1, C2 и C3,
потребности которых в течение одного
и того же периода составляют соответственно
10, 13 и 7 тыс. изделий. Стоимости перевозок
1 тыс. изделий потребителю с фабрик
приведены в таблице:
-
Фабрика
Потребители
C1
C2
C3
F1
5
4
6
F2
6
3
2
Сформулируйте
задачу нахождения оптимальных планов
производства и распределения как
транспортную и найдите ее решение.
4.
Компания контролирует три фабрики F1,
F2, F3, способные произвести 50, 25 и 25 тыс.
изделий еженедельно. Она заключила
договоры с заказчиками С1, С2, С3 и С4,
которым требуется еженедельно 15, 20, 20 и
30 тыс. изделий. Стоимости производства
и транспортировки 1 тыс. изделий заказчикам
с фабрик приведены ниже:
|
Фабрика |
Заказчик |
|||
|
С1 |
С2 |
С3 |
С4 |
|
|
F1 |
13 |
17 |
17 |
14 |
|
F2 |
18 |
16 |
16 |
18 |
|
F3 |
12 |
14 |
19 |
17 |
Определите
минимизирующую стоимость, объемы
производства и распределения для каждой
фабрики.
5.
Четыре сталелитейных завода производят
еженедельно соответственно 950, 300, 1350 и
450 т стали. Стальные болванки должны
быть преданы потребителям А, В, С, Е и Д,
еженедельные запросы которых составляют
250, 1000, 700, 650 и 450 т стали.
Стоимость
транспортировки от заводов к потребителям
приведена в таблице:
|
Завод |
Потребитель |
||||
|
А |
В |
С |
Д |
Е |
|
|
1 |
12 |
16 |
21 |
19 |
32 |
|
2 |
4 |
4 |
9 |
5 |
24 |
|
3 |
3 |
8 |
14 |
10 |
26 |
|
4 |
24 |
33 |
36 |
34 |
49 |
Какой
нужно составить план, чтобы минимизировать
общую стоимость?
6.
Четыре предприятия Староюрьевского
района используют для производства
используют некоторое сырьё. Спрос на
сырьё каждого из предприятий составляет
соответственно 120, 50, 190 и 110 условных
единиц. Сырьё сосредоточенно в тех
местах. Предложения поставщиков сырья
равны 160, 140 и 170 усл. Ед. На каждое
предприятие сырьё может завозиться от
любого поставщика. Тарифы перевозок
составляют соответственно 78, 121 и 91 усл.
Ед. Под тарифом понимается стоимость
перевозки единицы сырья. Требуется
составить план перевозок при котором
общая стоимость сырья минимальна.
7.
Компания владеет четырьмя заводами.
Соответствующие стоимости производства
равны 26, 54, 23 и 22 на единицу. Объем
производства 6000, 3000, 4500 и 3000 единиц.
Компания обязалась поставлять
соответственно 2500, 2700 и 3300 единиц в три
различных города. При заданных стоимостях
перевозок составьте оптимальные планы
производства и распределения.
|
Город |
Стоимость |
|||
|
А |
В |
С |
Д |
|
|
W |
1 |
9 |
6 |
8 |
|
X |
4 |
2 |
1 |
1 |
|
Z |
9 |
8 |
3 |
4 |
8.
Сталеплавильная компания располагает
двумя заводами, способными произвести
за некоторый промежуток времени 50 и
20итыс. Тонн стали соответственно. Свою
продукцию Компании поставляют четырем
различным потребителям, потребности
которых составляют соответственно 12,
15, 5 и 16 тыс. тонн.
Стоимости
производства и транспортировки приведены
в таблице.
|
Потребитель |
Завод |
|
|
М1 |
М2 |
|
|
С1 |
15 |
19 |
|
С2 |
19 |
18 |
|
С3 |
19 |
18 |
|
С4 |
15 |
19 |
9.
Компания контролирует 4 фабрики, способные
произвести 50, 30, 25 и 25 тыс. тонн изделий
еженедельно. Она заключила договоры с
пятью заказчиками, которым требуется
еженедельно 15, 20, 30, 20 и 30 тыс. изделий.
Стоимости производства и транспортировки
1 тыс. изделий заказчикам с фабрик
приведены ниже.
|
Фабрика |
Заказчик |
||||
|
1 |
2 |
3 |
4 |
5 |
|
|
1 |
13 |
17 |
17 |
14 |
14 |
|
2 |
18 |
16 |
16 |
18 |
18 |
|
3 |
12 |
14 |
19 |
17 |
17 |
|
4 |
11 |
15 |
21 |
13 |
12 |
Определите
оптимальный план перевозок, минимизирующий
затраты.
10.
Четыре сталелитейных завода производят
еженедельно соответственно 1150, 200, 1650 и
1450 т стали определенного сорта. Стальные
болванки должны быть переданы пяти
потребителям, еженедельные запросы
которых составляют 450, 1260, 200, 687, 450 тонн.
Стоимость транспортировки от заводов
к потребителям приведена в таблице.
|
Завод |
Потребитель |
||||
|
А |
В |
С |
Д |
Е |
|
|
1 |
17 |
14 |
23 |
12 |
52 |
|
2 |
5 |
3 |
10 |
7 |
23 |
|
3 |
10 |
5 |
15 |
18 |
18 |
|
4 |
12 |
21 |
42 |
34 |
49 |
Какой
нужно составить план распределения
продукции, чтобы минимизировать общую
стоимость.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

Главная Контакты Случайная статья
|
||||||
|
⇐ ПредыдущаяСтр 2 из 21Следующая ⇒ Масло |
||||||
| X | Y | Z | W | А | В | С |
Предполагая, что необработанная нефть доступна в неограниченном количестве, решить задачу максимизации прибыли.
Задача № 4
Компания контролирует три фабрики Ф1, Ф2, ФЗ, способные произвести 50, 25 и 25 тыс изделий. Она заключила договора с четырьмя заказчиками Cl, C2, СЗ и С4, которым требуется еженедельно 15, 20, 20, 30 тыс. изделий. Стоимость производства и транспортировки 1 тыс. изделий заказчикам с фабрик приведены ниже:
Фабрика
Заказчик
С1
С2
C3
С4
Ф1
Ф2
ФЗ
Определите минимизирующие общую стоимость, объемы производства и распределения для каждой фабрики.
Задача № 5
Производитель безалкогольной продукции располагает двумя разливочными машинами А и В. Машина А спроектирована для пол-литровьк бутылок, а машина В — для литровых, но каждая из них может использоваться для обоих типов бутылок с некоторой потерей эффективности в соответствии с приведенными в таблице данными о работе машин.
|
Кол-во бутылок, производимых в 1 мин. |
||
| Пол-литровые бутылки | Литровые бутылки | |
| А | ||
| В |
Каждая из машин работает ежедневно по 6 часов пятидневной рабочей недели. Прибыль от пол-литровой бутылки составляет 4 цента, а от литровой 10 центов. Недельная продукция не может превосходить 50000 литров, рынок принимает не более 44000 пол-литровых и 30000 литровых бутылок. Производитель хочет максимизировать свою прибыль при имеющихся средствах.
Задача № 6
Сталеплавильная компания располагает тремя заводами, способными произвести за некоторый промежуток времени 50, 30, 20 тыс. т. стали соответственно. Свою продукцию компания отправляет четырем потребителям С1, С2, СЗ, С4, потребности которых соответственно составляют 12, 15, 25, 36 тыс. тонн. Стоимость производства и транспортировки 1 тыс. т. стали с различных заводов различным потребителям приведены ниже.
Потребность
Завод
Ml
М2
M3
Cl
С2
СЗ
С4
Определите минимальную общую стоимость объема производства на каждом заводе и планы перевозок.
Задача № 7
Средства очистки пола оцениваются по следующим показателям:
1) очищающие свойства,
2) дезинфицирующие свойства,
3) раздражающее воздействие на кожу.
Каждый из этих показателей измеряется по линейной шкале от 0 до 100 единиц. Продукт на рынке должен иметь, по крайней мере, 60 единиц очищающих свойств и, по крайней мере, 60 единиц дезинфицирующих свойств по соответствующей шкале. При этом раздражающее воздействие на кожу должно быть минимальным. Конечный продукт должен быть смесью 3 основных очистителей, характеристики которых приведены в таблице.
| Очиститель | Очищающее свойство | Дезинфицирующее свойство | Раздражающее свойство |
| А | |||
| В | |||
| С |
Как смешать эти очистители, чтобы минимизировать раздражающее воздействие и удовлетворить ограничениям?
Задача № 8.
На 3-х нефтебазах некоей фирмы имеется 15000, 25000 и 20000 тонн горючего. Для собственных автозаправочных станций необходимо перевезти 20000, 12000, 5000, 8000 тонн. Цена перевозки 1000 тонн от базы до станции приведена в таблице. Спланировать перевозку горючего с целью минимизации затрат.
Базы
Автозаправочные станции
С1
С2
C3
С4
Б1
Б2
БЗ
Задача 9
Небольшая фирма производит два типа подшипников А и В, каждый из которых должен быть обработан на 3 станках — токарном, сверлильном и шлифовальном. Время, необходимое для каждой из стадий производственного процесса приведено в таблице.
|
Тип подшипника |
Время обработки
Токарный
Шлифовальный
Сверлильный
Прибыль от продажи одного подшипника
А
0,01
0,02
0,04
В
0,02
0,01
0,01
Полное возможное время работы в неделю
Фирма хотела бы производить подшипники в количествах, максимизирующих ее прибыль.
Задача №10.
Компания имеет три фабрики Ф1, Ф2, ФЗ, способные произвести 55, 27,5 и 27,5 тыс. изделий. Она заключила договора с четырьмя заказчиками С1, С2, СЗ и С4, которым требуется еженедельно 16,5, 22, 22, 33 тыс. изделий. Стоимость производства и транспортировки 1 тыс. изделий заказчикам с фабрик приведены ниже:
|
Фабрика |
Заказчик |
|||
| С1 | С2 | C3 | С4 | |
| Ф1 | 14,3 | 18,7 | 18,7 | 15,4 |
| Ф2 | 19,8 | 17,6 | 17,6 | 19,8 |
| ФЗ | 13,2 | 15,4 | 20,9 | 18,7 |
Определите минимизирующие общую стоимость, объемы производства и распределения для каждой фабрики.
Задача № 11
Сталеплавильная компания располагает тремя заводами, способными произвести за некоторый промежуток времени 100, 60, 40 тыс. т. стали соответственно. Свою продукцию компания отправляет четырем потребителям С1, С2, СЗ, С4, потребности которых соответственно составляют 24, 30, 50, 72 тыс. тонн. Стоимость производства и транспортировки 1 тыс. т. стали с различных заводов различным потребителям приведены ниже.
Потребность
Завод
Ml
М2
M3
Cl
С2
СЗ
С4
Определите минимальную общую стоимость объема производства на каждом заводе и планы перевозок.
Задача № 12
Производитель элементов центрального отопления изготовляет радиаторы 4 моделей. Ограничения на производство обусловлены количеством рабочей силы (не более 1000 человеко-часов) и количеством металлических листов (2000 кв.м.), из которых изготовляются радиаторы.
| Модель радиатора | А | В | С | Д |
| Необходимое количество рабочей силы, человеко-часы | 0,5 | 1,5 | 1,5 | |
| Необходимое количество стального листа, кв.м. | .2 | |||
| Прибыль от продажи одного радиатора, долл. | 12,5 |
Решить задачу с максимизацией прибыли в качестве целевой функции.
Задача № 13.
Компания контролирует три фабрики Ф1, Ф2, ФЗ, способные произвести 500, 250 и 250 тыс изделий. Она заключила договора с четырьмя заказчиками Cl, C2, СЗ и С4, которым требуется еженедельно 150, 200, 200, 300 тыс. изделий. Стоимость производства и транспортировки 1 тыс. изделий заказчикам с фабрик приведены ниже:
Фабрика
Заказчик
С1
С2
C3
С4
Ф1
Ф2
ФЗ
Определите минимизирующие общую стоимость, объемы производства и распределения для каждой фабрики.
Задача № 14
Аудитории и лаборатории университета рассчитаны не более чем на 500 студентов. Университет не принимает более 4000 студентов своей страны, но разрешает прием любого количества иностранных студентов. Персонал университета составляет 440 человек. Для обучения 12 студентов данной страны и 10 студентов — иностранцев требуется один преподаватель. Необходимо, чтобы 40% студентов данной страны и 80% иностранных могли разместиться в аудиториях, где имеется 2800 мест. Университет получает 2000 Евро в год из правительственных средств на каждого студента своей страны и берет плату в размере 3000 Евро в год за каждого иностранного студента. Предположив, что единственной целью университета является максимизация прибыли, определите, какой прием студентов своей страны и иностранных студентов следует планировать?
Задача № 15.
Сталеплавильная компания располагает тремя заводами, способными произвести за некоторый промежуток времени 55, 34, 21 тыс. т. стали соответственно. Свою продукцию компания отправляет четырем потребителям С1. С2. СЗ. С4, потребности которых соответственно составляют 19. 29. 27. 35 тыс. тонн. Стоимость производства и транспортировки 1 тыс. т. стали с различных- заводов различным потребителям приведены ниже.
|
Потребность |
Завод |
||
| Ml | М2 | M3 | |
| Cl | |||
| С2 | |||
| СЗ | |||
| С4 |
Определите минимальную общую стоимость объема производства на каждом заводе и планы перевозок.
Задача № 16
Для нормального развития молодняка зверофермы, необходимо здоровое питание с соблюдением нормы выдачи питательных веществ. Требуется определить минимальные затраты при соблюдении диетологических норм.
| питательные вещества (на 1000 г. продукта) | мясо | кости | крупа | норма |
| белки | ||||
| жиры | ||||
| углеводы | ||||
| микроэлементы | ||||
| стоимость единицы пищи |
60 |
Задача № 17
Сталеплавильная компания располагает тремя заводами, способными произвести за некоторый промежуток времени 50, 30, 20 тыс. т. стали соответственно. Свою продукцию компания отправляет четырем потребителям CL С2. СЗ, С4, потребности которых соответственно составляют 12. 15. 25, 36 тыс. тонн. Стоимость производства и транспортировки 1 тыс. т. стали с различных заводов различным потребителям приведены ниже.
Потребность
Завод
Ml
М2
M3
Cl
С2
СЗ
С4
Задача № 18
Грабитель, забравшись в магазин, стоит перед выбором, каким товаром заполнить рюкзак, соблюдая следующие ограничения:
• вес рюкзака не более 25 кг.,
• объем не должен превышать 0,3 куб. м.
• Стоимость набранных товаров должна быть максимальной. Рассчитать характер и количество взятого товара. Необходимые характеристики товаров, имеющихся в наличии в магазине, приведены в таблице:
| Товар | Цена (руб.) | Вес (г) | Объем (куб. см) | Всего в наличии |
| Водка | ||||
| Вино | ||||
| Пиво | ||||
| Мясо | ||||
| Сыр | ||||
| Консервы (в асе.) | 5,5 |
Задача № 19
Сталеплавильная компания располагает тремя заводами, способными произвести за некоторый промежуток времени 55. 34, 21 тыс. т. стали соответственно. Свою продукцию компания отправляет четырем потребителям C1, С2, СЗ, С4, потребности которых соответственно составляют 19, 29, 27, 35 тыс. тонн. Стоимость производства и транспортировки 1 тыс. т. стали с различных заводов различным потребителям приведены ниже.
Потребность
Завод
Ml
М2
M3
CI
С2
СЗ
С4
Определите минимальную общую стоимость объема производства на каждом заводе и планы перевозок.
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна. |
Презентация на тему Транспортная задача
Содержание
-
1.
Транспортная задача -
2.
Компания контролирует три фабрики А1, А2, А3, -
3.
Компания контролирует три фабрики А1, А2, А3, -
4.
Компания контролирует три фабрики А1, А2, А3, -
5.
Стоимости транспортировки 1 тысячи изделий заказчикам -
6.
Математическая модель: Найти матрицу перевозок Х, такую чтобы -
7.
Решение в Excel =СУММ(B10:E10) =СУММ(B10:B12) =СУММПРОИЗВ(B4:E6;B10:E12) -
12.
Скачать презентацию -
13.
Похожие презентации
Компания контролирует три фабрики А1, А2, А3, способные произвести 50, 25 и 25 тысяч изделий ежедневно. Она заключила договоры с четырьмя заказчиками В1, В2, В3 и В4, которым ежедневно требуется 25, 20, 30 и 25 тысяч изделий
Слайды и текст этой презентации
Слайд 1
Транспортная задача
Компания контролирует три фабрики А1, А2, А3,

способные произвести 50, 25 и 25 тысяч изделий ежедневно.
Она заключила договоры с четырьмя заказчиками В1, В2, В3 и
В4,
которым ежедневно требуется 25, 20, 30 и 25 тысяч изделий
соответственно. Стоимости транспортировки 1 тысячи изделий
заказчикам с фабрик следующие:
Определить минимизирующий общую стоимость план
перевозок изделий от фабрик к заказчикам.
Слайд 2
Компания контролирует три фабрики А1, А2, А3,
способные

произвести 50, 25 и 25 тысяч изделий ежедневно.
Она
заключила договоры с четырьмя заказчиками В1, В2, В3 и В4,
которым ежедневно требуется 25, 20, 30 и 25 тысяч изделий
соответственно.
Составляем математическую модель задачи:
Пусть
количество изделий, перевозимых с i-й фабрики
j-му заказчику
Слайд 3
Компания контролирует три фабрики А1, А2, А3,
способные

произвести 50, 25 и 25 тысяч изделий ежедневно.
Она
заключила договоры с четырьмя заказчиками В1, В2, В3 и В4,
которым ежедневно требуется 25, 20, 30 и 25 тысяч изделий
соответственно.
Составляем математическую модель задачи:
Пусть
количество изделий, перевозимых с i-й фабрики
j-му заказчику
Слайд 4
Компания контролирует три фабрики А1, А2, А3,
способные

произвести 50, 25 и 25 тысяч изделий ежедневно.
Она
заключила договоры с четырьмя заказчиками В1, В2, В3 и В4,
которым ежедневно требуется 25, 20, 30 и 25 тысяч изделий
соответственно.
Составляем математическую модель задачи:
Пусть
количество изделий, перевозимых с i-й фабрики
j-му заказчику
Слайд 5
Стоимости транспортировки 1 тысячи изделий
заказчикам с фабрик

следующие:
Определить минимизирующий общую стоимость план
перевозок изделий от
фабрик к заказчикам.
Пусть
стоимость перевозки с i-й фабрики j-му
потребителю
матрица стоимостей
Слайд 6
Математическая модель:
Найти матрицу перевозок Х, такую чтобы

Слайд 7
Решение в Excel
=СУММ(B10:E10)
=СУММ(B10:B12)
=СУММПРОИЗВ(B4:E6;B10:E12)
Слайды презентации
Слайд 1
Транспортная задача
Компания контролирует три фабрики А1, А2, А3 ,
способные
произвести 50, 25 и 25 тысяч изделий ежедневно.
Она
заключила договоры с четырьмя заказчиками В1, В2, В3 и В4
,
которым ежедневно требуется 25, 20, 30 и 25 тысяч изделий
соответственно. Стоимости транспортировки 1 тысячи изделий
заказчикам с фабрик следующие:
Определить минимизирующий общую стоимость план
перевозок изделий от фабрик к заказчикам.
Слайд 2
Компания контролирует три фабрики А1, А2, А3 ,
способные произвести
50, 25 и 25 тысяч изделий ежедневно.
Она заключила
договоры с четырьмя заказчиками В1, В2, В3 и В4 ,
которым ежедневно требуется 25, 20, 30 и 25 тысяч изделий
соответственно. Составляем математическую модель задачи :
Пусть
ijx количество изделий, перевозимых с i- й фабрики
j- му заказчику
B1 B2 B3 B4
A1
A2
A3
11
x 12
x
13
x
14
x
21
x
22
x 23
x
24
x
31
x
32
x 33
x
34
x
Слайд 3
Компания контролирует три фабрики А1, А2, А3 ,
способные произвести
50, 25 и 25 тысяч изделий ежедневно.
Она заключила
договоры с четырьмя заказчиками В1, В2, В3 и В4 ,
которым ежедневно требуется 25, 20, 30 и 25 тысяч изделий
соответственно. Составляем математическую модель задачи :
Пусть
ijx количество изделий, перевозимых с i- й фабрики
j- му заказчику
B1 B2 B3 B4
A1
A2
A3
11
x 12
x
13
x
14
x
21
x
22
x 23
x
24
x
31
x
32
x 33
x
34
x 4
1
1
50 j
j x
4
2
1
25 j
j x
4
3
1
25 j
j x
Слайд 4
Компания контролирует три фабрики А1, А2, А3 ,
способные произвести
50, 25 и 25 тысяч изделий ежедневно.
Она заключила
договоры с четырьмя заказчиками В1, В2, В3 и В4 ,
которым ежедневно требуется 25, 20, 30 и 25 тысяч изделий
соответственно. Составляем математическую модель задачи :
Пусть
ijx количество изделий, перевозимых с i- й фабрики
j- му заказчику
B1 B2 B3 B4
A1
A2
A3
11
x 12
x
13
x
14
x
21
x
22
x 23
x
24
x
31
x
32
x 33
x
34
x
3
1
1
25 i
i x
3
2
1
20 i
i
x
3
2
1
30 i
i
x
4
2
1
25 i
i
x
Слайд 5
Стоимости транспортировки 1 тысячи изделий
заказчикам с фабрик следующие:
Определить
минимизирующий общую стоимость план
перевозок изделий от фабрик к
заказчикам.
Пусть ij
c стоимость перевозки с i- й фабрики j-
му
потребителю
13 17 17 14
18 16 16 18
12 14 19 17
C
матрица стоимостей
Слайд 6
Математическая модель :3 4
1 1
3 3 3 4
1 2 2
2
1 1 1 1
4 4 4
1 2 3
1 1
1
min
25, 20, 30, 25
50, 25, 25
0
ij ij
i j
i i i
i
i i i i
j j j
j j j
ij
c x
x x x x
x x x
x
Найти матрицу перевозок Х, такую чтобы
Слайд 7
Решение в Excel
= СУММ( B10:E10)
= СУММ( B10:B12)
=СУММПРОИЗВ(B4:E6;B10:E12)
Чтобы скачать презентацию — поделитесь ей с друзьями с помощью
социальных кнопок.







