Математика Профильный уровень
Часть 1
Ответом на задания 1—12 должно быть целое число или десятичная дробь.
1
1
Компания для украшения помещения к новому году закупила 7 искусственных ёлок. Для украшения одной ёлки требуется не менее 13 игрушек. Игрушки продаются комплектами по 10 штук. Сколько нужно закупить комплектов, чтобы украсить все ёлки?
2
2
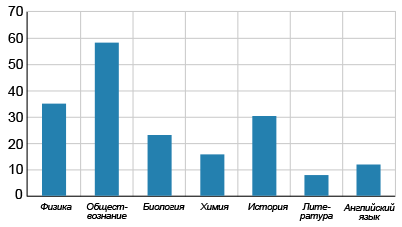
На диаграмме изображено количество учеников 11 класса, выбравших для сдачи ЕГЭ различные дополнительные экзамены. По горизонтали указаны экзамены, по вертикали — количество учеников, выбравших тот или иной экзамен. По диаграмме определите, сколько экзаменов были более востребованы, чем химия.
3
3
Найдите площадь равнобедренной трапеции (в см2), высота которой равна 7 см и делит основание на отрезки длиной 17 см и 6 см.
4
4
На производстве при упаковке чая вероятность того, что упаковка окажется не герметичной, равна 0,09. Найдите вероятность того, что две произвольно выбранные упаковки чая окажутся герметичными.
5
5
Решите уравнение [math]sqrt{frac{3x-5}{2x}}=frac13[/math]
6
6
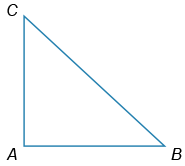
В прямоугольном треугольнике ABC угол A равен 90°. Найдите сторону AC (в см), если tg∠C=[math]frac74[/math], CB=[math]2sqrt{65}[/math] см.
7
7
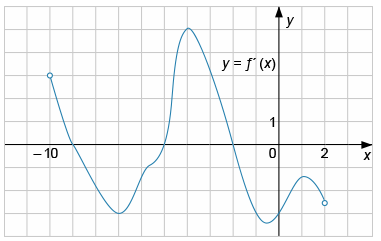
На рисунке представлен график производной функции y=f ‘(x) на интервале (−10; 2). Найдите точку минимума функции y=f(x) на данном промежутке.
8
8
Объём прямоугольного параллелепипеда, в основании которого лежит квадрат, равен 200 см3. Найдите площадь его боковой поверхности (в см2), если высота параллелепипеда равна 8 см.
9
9
Найдите значение выражения [math]frac{log_5125}{log_frac139}[/math]
10
10
Координата тела при равноускоренном движении изменяется по закону [math]x=x_0+v_0t+frac{at^2}2[/math], где [math]x_0[/math] — начальная координата тела, a — ускорение тела, t — время движения тела. Найдите время движения тела, если его ускорение равно 2 м/c2, начальная координата равна 7 м, а координата в конце движения равна 67 м при начальной скорости 11 м/с.
11
11
Из одного порта в другой по течению выплыл плот, через два часа ему навстречу выплыла моторная лодка, они встретились через 4 часа после отправления лодки. Найдите скорость лодки (в км/ч), если скорость течения равна 3 км/ч, а расстояние между портами равно 146 км.
12
12
Найдите наименьшее значение функции [math]y=4x+frac1x+7[/math] на промежутке (0;2)
Часть 2.
При выполнении заданий 13—19 требуется записать полное решение и ответ.
13
Дано уравнение 4cos4x — 5cos2x — 1 = 0.
А) Решите уравнение.
Б) Укажите корни этого уравнения, принадлежащие отрезку [arccos0; arccos(-1)].
Показать ответ
А) Преобразуем уравнение:
[math]4(frac{1+cos2x}2)^2-5cos2x-1=0[/math]
[math]1+2cos2x+cos^22x-5cos2x-1=0[/math]
[math]cos^22x-3cos2x=0[/math]
[math]cos2x(cos2x-3)=0[/math]
т.е. имеем, что [math]cos2x=0[/math] или [math]cos2x-3=0[/math]
В первом случае [math]2x=fracpi2+pi n[/math]; [math]x=fracpi4+frac{pi n}2[/math], [math]nin Z[/math]
Во втором случае [math]varnothing[/math], так как не соответствует области значений косинуса
Б) Нанесем корни на числовую прямую и определим, какие корни входят в отрезок:
Ответ:
А) [math]fracpi4+frac{pi k}2;;kin Z;[/math]
Б) [math]frac{3pi}4[/math]
14
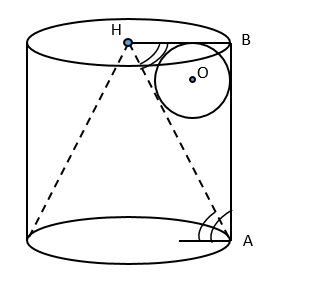
Цилиндр и конус имеют общее основание, вершина конуса является центром другого основания цилиндра. Каждая образующая конуса наклонена к плоскости основания под углом 30°.
А) Докажите, что площади боковых поверхностей цилиндра и конуса равны.
Б) Найдите радиус сферы, касающейся боковых поверхностей цилиндра и конуса, а также одного из оснований цилиндра, если известно, что объем конуса равен [math]left(6sqrt3+10right)cdotpi[/math].
Показать ответ
А) [math]S_{б.к.}=S_{б.ц.}[/math] — доказать
[math]S_{б.к.}=pi rcdot AH[/math] ; [math]S_{б.ц.}=2pi rcdot AB[/math]
Рассмотрим [math]bigtriangleup ABH[/math], [math]H[/math] — центр основания цилиндра, [math]BAperp[/math] нижнему основанию цилиндра, [math]angle B=90^circ[/math]
[math]sin(angle H)=frac{AB}{AH}=sin(30^circ)=frac12Rightarrow AB=frac12AH[/math]
[math]Rightarrow S_{б.ц.}=2pi rcdotfrac12AH=pi rcdot AH=S_{б.к.}[/math], что и требовалось доказать
Б) [math]V_к=(6sqrt3+10)pi[/math], [math]r_0[/math] — ?
т. [math]О[/math] — центр сферы, пусть т. [math]Oin(ABH)[/math]
[math]Rightarrow r_0=[/math] радиусу вписанное в [math]bigtriangleup ABH[/math] окружности
[math]Rightarrow r_0=frac{HB+AB-AH}2=frac{R+h-frac h{sin(angle H)}}2=frac{R-h}2[/math]
[math]frac hR=tg(angle H)Rightarrow h=Rcdot tg(30^circ)=frac{Rsqrt3}3[/math]
[math]V_к=frac13pi R^2h=frac13pi R^2cdotfrac{Rsqrt3}3=frac{pi R^3sqrt3}9[/math], [math]r_0=frac{R(1-frac{sqrt3}3)}2Rightarrow R=frac{2r_0}{1-frac{sqrt3}3}[/math]
[math]Rightarrowfrac{pisqrt3}9cdot(frac{2r_0}{1-frac{sqrt3}3})^3=(6sqrt3+10)pi[/math]
[math]frac{8sqrt3}9r_0^3=12sqrt3-20+20-frac{100sqrt3}9[/math]
[math]r_0^3=1[/math]
[math]r_0=1[/math]
Ответ: 1
15
Решите неравенство [math]frac{log_3sqrt{28cdot3^x-3}}{x+1}geq1[/math].
Показать ответ
Перенесем единицу в левую часть и приведем к общему знаменателю:
[math]frac{log_3sqrt{28cdot3^x-3}-(x+1)}{x+1}geq0[/math]
ОДЗ: [math]28cdot3^x-3>0[/math]
[math]x>log_3frac3{28}[/math]
[math]x>1-log_328[/math]
Нули числителя: [math]frac12log_3(28cdot3^x-3)-(x+1)=0[/math]
[math]log_3(28cdot3^x-3)=2(x+1)[/math]
[math]28cdot3^x-3=3^{2(x+1)}[/math]
[math]9cdot3^{2x}-28cdot3^x+3=0[/math]
D=646
[math]3^x=frac{28+26}{18}=3Rightarrow x=1[/math]
[math]3^x=frac{28-26}{18}=frac19Rightarrow x=-2[/math]
Нули знаменателя:[math]x+1=0Rightarrow x=-1[/math]
Нанесем нули на числовую прямую, расставим знаки, при этом учитываем ОДЗ:
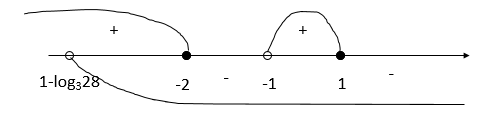
Ответ: (1-log328; -2]⋃(-1; 1]
16
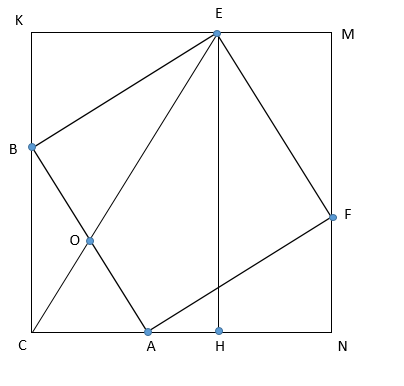
В прямоугольном треугольнике АВС известно, что ВС=2⋅АС. На гипотенузе АВ вне треугольника построен квадрат ABEF. Прямая СЕ пересекает АВ в точке О.
А) Докажите, что ОА:ОВ=3:4.
Б) Найдите отношение площадей треугольников АОС и ВОЕ.
Показать ответ
А) Достроим до квадрата [math]CKMN[/math] так, чтобы [math]bigtriangleup ABC=bigtriangleup FAN=bigtriangleup EFM=bigtriangleup BEK[/math]
Обозначим [math]angle OCA=alpha[/math] и запишем теорему синусов для [math]bigtriangleup OCA[/math] и [math]bigtriangleup OCB[/math]:
[math]frac{OC}{sin(angle OBC)}=frac{OB}{sinn(90^circ-alpha)}[/math]
[math]Rightarrowfrac{OA}{OB}cdotfrac{cosalpha}{sinalpha}=frac{sin(angle OBC)}{sin(angle OAC)}[/math]
[math]Rightarrowfrac{OA}{OB}=frac{sin(angle OBC)}{sin(angle OAC)}cdot tgalpha[/math]
Опустим из Е перпендикуляр на CN. [math]EHperp CN;EH=MN=CA+BC=3AC[/math]
[math]HN=EM[/math] (по свойству прямоугольника [math]EMNH[/math])
[math]Rightarrow CH=CN-HN=3AC-AC=2AC[/math]
[math]Rightarrow tg(angle ECH)=tgalpha=frac32[/math]
Рассмотрим [math]bigtriangleup ABC[/math]: по теореме Пифагора [math]AB=sqrt{AC^2+BC^2}=sqrt{AC^2+4AC^2}=sqrt5AC[/math]
[math]sin(angle ABC)=sin(angle OBC)=frac{AC}{sqrt5AC}=frac1{sqrt5}[/math]
[math]sin(angle BAC)=sin(angle OAC)=frac{2AC}{sqrt5AC}=frac2{sqrt5}[/math]
[math]Rightarrowfrac{OA}{OB}=frac1{sqrt5}cdotfrac{sqrt5}2cdotfrac32=frac34[/math], ч.т.д.
Б) [math]frac{S_{bigtriangleup AOC}}{S_{bigtriangleup BOE}}-?[/math]
[math]S_{bigtriangleup AOC}=frac12AOcdot ACcdot sin(angle AOC)=frac12cdotfrac37ABcdot ACcdotfrac2{sqrt5}=frac3{7sqrt5}ACcdotsqrt5cdot AC=frac37AC^2[/math]
[math]S_{bigtriangleup BOE}=frac12BOcdot BE=frac12cdotfrac47cdot ABcdot AB=frac27cdotleft(ACsqrt5right)^2=frac{10}7AC^2[/math]
[math]Rightarrowfrac{S_{bigtriangleup AOC}}{S_{bigtriangleup BOE}}=frac{frac37AC^2}{frac{10}7AC^2}=frac3{10}[/math]
Ответ: 0,3
17
16 ноября близнецы Саша и Паша взяли в банке кредит по 500 тысяч руб. каждый сроком на четыре месяца. Условия возврата кредита таковы:
• 28-го числа каждого месяца долг увеличивается на 10 % по сравнению с 16-м числом текущего месяца;
• с 1-го по 15-е число каждого месяца необходимо выплатить часть долга; 16-го числа каждого месяца долг должен составлять некоторую сумму в соответствии с предложенной для каждого из них таблицей:
Саша
| Дата | 16.11 | 16.12 | 16.01 | 16.02 | 16.03 |
| Долг, тыс. руб. | 500 | 300 | 200 | 100 | 0 |
Паша
| Дата | 16.11 | 16.12 | 16.01 | 16.02 | 16.03 |
| Долг, тыс. руб. | 500 | 400 | 300 | 200 | 0 |
Kто из братьев за четыре месяца выплатит банку меньшую сумму? На сколько рублей?
Показать ответ
Решение:
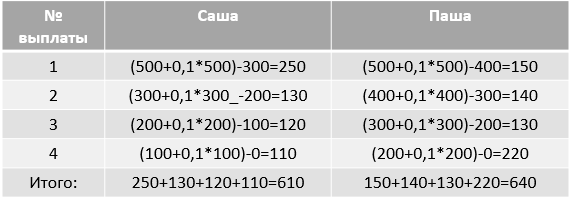
Составим таблицу выплат каждого из близнецов и посчитаем итоговую сумму выплаты по каждому:
Получим, что Саша выплатит меньше на 30 тыс. ( 640-610=30)
Ответ: Саша выплатит меньше на 30 тыс.
18
Найдите все а, при каждом из которых в область значений функции [math]y=frac{8x-a-6}{8x^2+8}[/math] входит ровно два целых числа. Для каждого такого а укажите эти целые числа.
Показать ответ
Решение: так как нам дана дробь, и числитель является линейной функцией , то какое бы a мы не взяла всегда найдется значение х, в котором числитель равен 0, соответственно и исходная функция. ( такой же вывод можно сделать из предела функции)
Исходная функция непрерывна на [math]xin R[/math]. Требуется по условию, что в область значений входит только два целых числа, значит имеем два варианта: 0 и 1, 0 и -1. Рассмотрим два случая.
1 сл: 0 и 1
Решим уравнение:
[math]frac{8x-a-6}{8x^2+8}=1[/math]
[math]8x^2-8x+a+14=0[/math]
[math]D=64-32(a+14)geq0[/math]
[math]aleq-12[/math]
Учтем, что значения функции в данном случае лежит в пределах [math](-1;2)[/math] при [math]xin R[/math]
Решим неравенство [math]-1<frac{8x-a-6}{8x^2+8}<2[/math].
Решение: [math]a>-21;a<0[/math]. Получим, учитывая область значений функции, что [math]ain(-21;-12rbrack[/math]
2 сл: 0 и -1
Решим уравнение:
[math]frac{8x-a-6}{8x^2+8}=-1[/math]
[math]8x^2+8x-a+2=0[/math]
[math]D=64-32(-a+2)geq0[/math]
[math]ageq0[/math]
Учтем, что значения функции в данном случае лежит в пределах [math](-2;1)[/math] при [math]xin R[/math]
Решим неравенство [math]-2<frac{8x-a-6}{8x^2+8}<1[/math].
Решение: [math]a>-12;a<9[/math]. Получим, учитывая область значений функции, что [math]ainlbrack0;9)[/math]
Ответ: a∈(-21; -12]⋃[0; 9);
при а∈(-21; -12] y=0 и y=1;
при а∈[0; 9) y=0 и y=-1
19
А) Каждая точка плоскости окрашена в один из двух цветов. Обязательно ли на плоскости найдутся две точки одного цвета, удаленные друг от друга ровно на 1 м?
Б) Каждая точка прямой окрашена в один из 10 цветов. Обязательно ли на прямой найдутся две точки одного цвета, удаленные друг от друга на целое число метров?
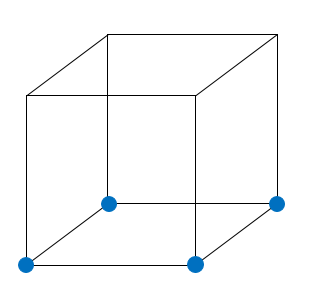
В) Какое наибольшее количество вершин куба можно покрасить в синий цвет так, чтобы среди синих вершин нельзя было выбрать три, образующие равносторонний треугольник?
Показать ответ
А) Предположим, что для произвольной точки плоскости все точки, удаленные от нее ровно на 1 м, другого цвета (если среди них были бы точки того же цвета, то это бы означало, что для этой произвольной точки нашлась точки того же цвета и задача была решена изначально). Следовательно, мы получим окружность радиуса 1 м, центр которой — точка одного цвета, а все точки окружности — точки другого цвета. На окружности всегда найдется хорда, равная радиусу окружности, следовательно мы найдем две точки одного цвета ( на концах хорды), отстоящих друг от друга на длину хорды, т.е. 1м. Ответ : да, можно
Б) Вероятность точки прямой определенного цвета 1/10. Следовательно из 20 точек прямой точки одного цвета попадут минимум 2 раза. Разместим точки разных десяти цветов на одинаковом целочисленном расстоянии друг от друга, тогда 11 точка будет совпадать с цветом любой из предыдущих, так как точки размещены всех 10ти цветов. Значит ответ:да, можно
В) Можно выбрать 4 вершины (вершины одной грани, они не образуют равносторонний треугольник). Если берем пять вершин, то можно составить равносторонний треугольник. На рисунке приведено решение:
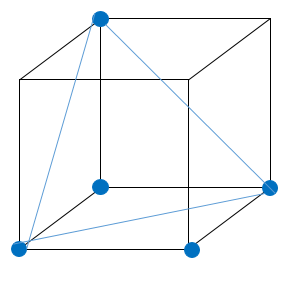
Ответ: А) да; Б) да; В) 4.
👋 Привет Лёва
Середнячок
40/250
Задать вопрос

nargizibraeva0
+10
Решено
2 года назад
Математика
5 — 9 классы
Задача. В том году в магазине к новому году купили 200 ёлок. В этом году количество купленных ёлок увеличилось на 120%. Сколько ёлок купили в этом году?даю за правильный ответ 5 звёзд
Смотреть ответ
1
Ответ
2
(2 оценки)
1
ekaterina13041989
2 года назад
Светило науки — 748 ответов — 256 раз оказано помощи
Ответ:
от 200 =120%=200÷100×120=240
200+240=440 ёлок
(2 оценки)
https://vashotvet.com/task/12062453
В каком случае учитываются расходы на приобретение елки и игрушек при исчислении налога на прибыль?
Вопрос: Организация к новогоднему празднику приобрела елку и новогодние игрушки. При каких условиях налогооблагаемую базу можно уменьшить на понесенные расходы при исчислении налога на прибыль, а при каких — нет? Необходимо ли составлять приказ о покупке новогодних украшений?
Ответ: Расходы на приобретение елки и новогодних игрушек можно включить в налоговую базу по налогу на прибыль, в случае если указанные расходы направлены на получение дохода, например, от организации отдыха и развлечений, культуры и спорта, либо иного их использования, связанного с предпринимательской деятельностью (реклама, представительские расходы).
Также указанные расходы возможно включить в состав прочих расходов, если указанные расходы произведены организацией, соответствующей требованиям пп. 38 или 39 п. 1 ст. 264 Налогового кодекса РФ.
Издавать приказ о покупке новогодних украшений не требуется.
Затраты на приобретение елки и новогодних игрушек, приобретенных не для предпринимательской деятельности, например, для празднования Нового года в организации, не могут быть учтены в составе расходов, уменьшающих налогооблагаемую базу по налогу на прибыль.
Обоснование: Согласно положениям ст. 252 НК РФ расходами признаются любые обоснованные и документально подтвержденные затраты при условии, что они произведены для осуществления деятельности, направленной на получение дохода.
Соответственно, затраты, направленные на приобретение елки и новогодних игрушек, могут быть признаны обоснованными, в случае если направлены на получение дохода, а это, как правило, деятельность, связанная с организацией отдыха и развлечений, культуры и спорта.
В соответствии с пп. 38 п. 1 ст. 264 НК РФ к прочим расходам, связанным с производством и реализацией, относятся расходы, осуществленные налогоплательщиком-организацией, использующей труд инвалидов, в виде средств, направленных на цели, обеспечивающие социальную защиту инвалидов, если от общего числа работников такого налогоплательщика инвалиды составляют не менее 50 процентов и доля расходов на оплату труда инвалидов в расходах на оплату труда составляет не менее 25 процентов.
Целями социальной защиты инвалидов в соответствии с законодательством Российской Федерации о социальной защите инвалидов признаются мероприятия по интеграции инвалидов в общество (включая культурные, спортивные и иные подобные мероприятия).
Также в соответствии с пп. 39 п. 1 ст. 264 НК РФ к прочим расходам относятся расходы налогоплательщиков — общественных организаций инвалидов, а также налогоплательщиков-учреждений, единственными собственниками имущества которых являются общественные организации инвалидов, в виде средств, направленных на осуществление деятельности указанных общественных организаций инвалидов и на цели, указанные в пп. 38 п. 1 ст. 264 НК РФ.
В силу пп. 28 п. 1 ст. 264 НК РФ расходы на рекламу производимых (приобретенных) и (или) реализуемых товаров (работ, услуг), деятельности налогоплательщика, товарного знака и знака обслуживания, включая участие в выставках и ярмарках, также относятся к прочим расходам, связанным с производством и реализацией, с учетом положений п. 4 ст. 264 НК РФ.
Затраты на приобретение елки и новогодних игрушек в ряде случаев можно учесть в составе прочих расходов, связанных с производством и реализацией, как затраты на рекламу, в связи с тем что зачастую организации при помощи новогоднего оформления витрин стараются привлечь внимание потенциального клиента к себе или к своей продукции. Но в зависимости от конкретной ситуации не исключены споры с контролирующими органами.
Например, Решением Арбитражного суда Челябинской области от 24.12.2007 по делу N А76-24215/2007 (оставлено в силе Постановлением Президиума ВАС РФ от 25.02.2009 N 12664/08) признаны обоснованными затраты на приобретение елки и новогодних украшений. В Постановлении ФАС Московского округа от 27.06.2011 по делу N А40-55988/10-142-307 также сделан вывод о том, что произведенные затраты на новогоднее оформление гирляндами, фонарями и другой иллюминацией отвечают требованиям пп. 28 п. 1 ст. 264 НК РФ.
Противоположный вывод сделан в Постановлениях ФАС Западно-Сибирского округа от 15.12.2010 N А70-6645/2009 и ФАС Поволжского округа от 01.10.2009 N А55-1113/2009, в которых суды пришли к выводу, что расходы на оформление территории и помещений организации предметами украшательства (елками, елочными изделиями, плакатами и т.д.), которые, по ее мнению, являются рекламными, не направлены на получение дохода, экономически неэффективны, не относятся к рекламной деятельности, соответственно, не могут быть учтены в целях исчисления налога на прибыль.
Расходы на приобретение елки и новогодних игрушек могут быть связаны с представительскими расходами, если они используются на официальных приемах, встречах, направленных на поддержание (установление) взаимного сотрудничества с контрагентами.
Согласно пп. 22 п. 1 ст. 264 НК РФ к прочим расходам, связанным с производством и реализацией, относятся представительские расходы, связанные с официальным приемом и обслуживанием представителей других организаций, участвующих в переговорах в целях установления и поддержания сотрудничества, в порядке, предусмотренном п. 2 данной статьи.
В силу п. 2 ст. 264 НК РФ к представительским расходам относятся расходы налогоплательщика на официальный прием и (или) обслуживание представителей других организаций, участвующих в переговорах в целях установления и (или) поддержания взаимного сотрудничества, а также участников, прибывших на заседания совета директоров (правления) или иного руководящего органа налогоплательщика, независимо от места проведения указанных мероприятий. К представительским расходам относятся расходы на проведение официального приема (завтрака, обеда или иного аналогичного мероприятия) для указанных лиц, а также официальных лиц организации-налогоплательщика, участвующих в переговорах, транспортное обеспечение доставки этих лиц к месту проведения представительского мероприятия и (или) заседания руководящего органа и обратно, буфетное обслуживание во время переговоров, оплата услуг переводчиков, не состоящих в штате налогоплательщика, по обеспечению перевода во время проведения представительских мероприятий. Представительские расходы в течение отчетного (налогового) периода включаются в состав прочих расходов в размере, не превышающем 4 процентов от расходов налогоплательщика на оплату труда за этот отчетный (налоговый) период.
В Постановлении ФАС Уральского округа от 19.01.2012 по делу N А50-3964/2011 сделан вывод о правомерном включении налогоплательщиком в состав прочих расходов затрат на проведение официального представительского мероприятия (новогоднего праздника).
Таким образом, возможность учета расходов на приобретение елки и новогодних игрушек в налоговой базе по налогу на прибыль зависит от вида деятельности организации и конкретных обстоятельств, с которыми связано приобретение этих товаров.
Издавать приказ о покупке новогодних украшений не требуется.
В любом случае затраты на приобретение елки и новогодних игрушек, не связанные с предпринимательской деятельностью, например, для празднования Нового года в организации, не могут быть учтены в составе расходов, уменьшающих налогооблагаемую базу по налогу на прибыль, поскольку не отвечают требованиям ст. 252 НК РФ.
И.В.Просеков
Советник государственной
гражданской службы РФ
3 класса
15.07.2016