Какую минимальную работу нужно совершить чтобы за время t

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

2018-01-20   

Какую работу нужно совершить, чтобы за время $t = 10 мин$ подняться по движущемуся вниз эскалатору? Высота подъема равна $h = 10 м$, скорость эскалатора постоянна и равна $v_{э} = 0,5 м/с$, угол наклона эскалатора к горизонту равен $alpha = 40^{ circ}$. Масса человека $m = 70 кг$.

Решение:

По закону сложения скоростей $vec{v}_{з} = vec{ч} + vec{v}_{э}$, где $vec{v}_{з}$ — скорость человека относительно земли, $vec{v}_{ч}$ — скорость человека относительно эскалатора, $vec{v}_{э}$ — скорость движения эскалатора. В скалярном виде $v_{з} = v_{ч} — v_{э}$. Домножим все слагаемые на время движения $t$, получим $v_{з}t = v_{ч}t — v_{э}t$, где $v_{з}t = l = h/ sin alpha$ — длина эскалатора, $v_{э}t$ — путь, пройденный эскалатором, $v_{ч}t = S$ — расстояние, которое прошел человек относительно эскалатора. Тогда $S = l + v_{э}t = h / sin alpha + v_{э}t$. Во время подъема сила тяжести составляет угол $beta = 90^{ circ} + alpha$ с перемещением $S$. Работа, которую совершает человек, $A = mg (h/ sin alpha + v_{э}t ) | cos (90^{ circ} + alpha)| = mg (h / sin alpha + v_{э}t) sin alpha; A = 140 кДж$. Часть работы $mgh$ идет на увеличение потенциальной энергии человека, а другая часть $mgv_{э} t sin alpha$ вместе с работой мотора, приводящего эскалатор в движение, идет на преодоление сил трения.

№19450

Экзамены с этой задачей:

Предмет и тема: Физика, Механика, Закон сохранения энергии и импульса, Работа. Мощность. Энергия, Механическая работа,

Задача в следующих классах: 10 класс 11 класс

Сложность задачи : 2

Задача встречается в следующей книге: Турчина Н. В. и др. Физика: 3800 задач для школьников и поступающих в вузы //М.: Дрофа. – 2000. – Т. 3.

Условие

Какую минимальную работу нужно совершить, чтобы за время (t) подняться по движущемуся вниз эскалатору метро? Высота подъема (h), скорость эскалатора и, угол наклона эскалатора к горизонту равен (alpha) .

Ответ

NaN

Решение № 19441:

(A=mcdot gcdot (h+vcdot tcdot sincdot alpha ))

Спрятать решение

Спрятать критерии

Классификатор: Механика. Механическая работа и энергия

Минимальная работа

Cтраница 3

Минимальной работе сжижения соответствует следующее проведение процесса ( рис. 9.15): изотермическое сжатие АВ и изоэнтропическое расширение ВС.
 [31]

Такова минимальная работа, которую необходимо затратить для того, чтобы сжать 1 кг — моль SOa до давления конденсации при 25 С.
 [32]

Величина минимальной работы, так же как и в примере 1, не меняется, если процесс ведут любым другим обратимым способом, а не тем путем, который изображен нз диаграмме, так как / mm зависит только от начальной и конечной точек процесса.
 [34]

Величина минимальной работы на единицу разделяемой смеси равна Де6 о ев. Работа, отнесенная, например, к единице продукта с концентрацией Sjs.
 [36]

Отношение минимальной работы к реально затраченной характеризует термодинамическую эффективность процесса опреснения.
 [37]

Отношение теоретической минимальной работы к работе, расходуемой на сжижение ( конденсацию) газа, представляет собой коэффициент полезного действия холодильного оборудования ( см. табл. 76, стр.
 [38]

Какую минимальную работу нужно совершить, чтобы сдвинуть ось системы вправо на расстояние I, меньшее, чем расстояние до края пресса.
 [39]

Вычислите минимальную работу ( в джоулях), которую нужно затратить на замораживание одного литра воды с начальной температурой Г 20 С, если используется тепловой резервуар при температуре 20 С.
 [40]

Какую минимальную работу нужно затратить для того, чтобы заморозить 1 кг воды, находящейся при температуре окружающей среды 300 К.
 [41]

Какую минимальную работу необходимо совершить чтобы вынести пластину из электрического поля.
 [42]

Какую минимальную работу против сил электрического поля нужно совершить, чтобы собрать каплю ртути радиуса R с зарядом Q из N одинаковых заряженных капель.
 [43]

Какую минимальную работу нужно совершить, чтобы за время t подняться по движущемуся вниз эскалатору метро.
 [44]

Какую минимальную работу нужно совершить, чтобы поднять шарик на высоту Я 2 м над поверхностью воды.
 [45]

Страницы:  

   1

   2

   3

   4

Условие задачи:

Какую минимальную работу необходимо совершить, чтобы лежащий на столе груз массой 1 кг поднять на высоту 1 м при помощи привязанного к нему невесомого резинового жгута? В начальном состоянии жгут не растянут, его жесткость 10 Н/м.

Задача №2.8.24 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(m=1) кг, (h=1) м, (k=10) Н/м, (A-?)

Решение задачи:

Для начала груз нужно оторвать от стола. Так как груз поднимают резиновым жгутом, то перед тем как груз оторвется от стола, жгут растянется на некоторую величину (x). Как эту деформацию определить? Достаточно записать первый закон Ньютона для покоящегося груза в проекции на ось (y):

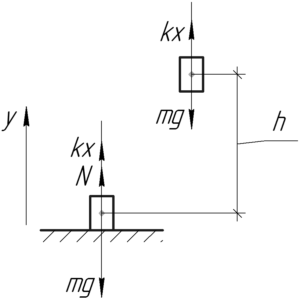
[N + kx – mg = 0]

Здесь (kx) – сила упругости резинового жгута, определяемое по закону Гука:

[{F_{у}} = kx]

Когда груз оторвется от стола, то сила реакции опоры (N) станет равной нулю. Тогда:

[N = 0 Rightarrow kx = mg]

[x = frac{{mg}}{k}]

После отрыва от стола груз поднимают равномерно с такой маленькой скоростью, что ею можно пренебречь, дабы соблюсти условие минимальности работы и не изменить величину деформации жгута (если груз поднимать равноускоренно, то деформация увеличится).

Далее воспользуемся законом сохранения энергии. Согласно ему работа внешней силы есть изменение полной механической энергии системы. В данном случае изменилась потенциальная энергия жгута и груза.

[A = Delta E]

В начале потенциальная энергия обоих тел равна нулю. Когда груз будет поднят на заданную высоту (h), то его потенциальная энергия будет равна ({E_{1}} = mgh), при этом жгут будет растянут на величину (x), а его потенциальная энергия будет равна ({E_{2}} = frac{{k{x^2}}}{2}).

[A = {E_1} + {E_2}]

[A = mgh + frac{{k{x^2}}}{2}]

Так как мы определили, что (x = frac{{mg}}{k}), то:

[A = mgh + frac{k}{2}{left( {frac{{mg}}{k}} right)^2} = mgh + frac{{{m^2}{g^2}}}{{2k}}]

[A = mgleft( {h + frac{{mg}}{{2k}}} right)]

Так как все численные значения величин даны в системе СИ, то можем сразу посчитать ответ:

[A = 1 cdot 10left( {1 + frac{{1 cdot 10}}{{2 cdot 10}}} right) = 15; Дж]

Ответ: 15 Дж.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.8.23 Мяч бросили под углом к горизонту со скоростью 20 м/с. Найти скорость мяча
2.8.25 На тело массой 1 кг, брошенное с поверхности Земли вертикально вверх с начальной
2.8.26 Пуля, летящая горизонтально со скоростью 510 м/с, попадает в ящик, лежащий