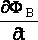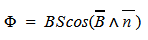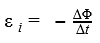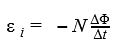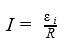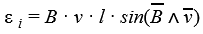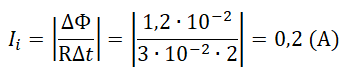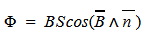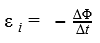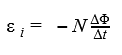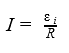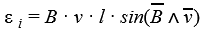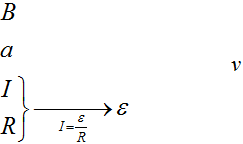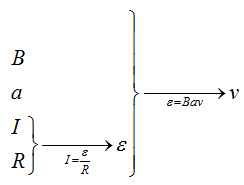Вопросы и задания для самоконтроля
-
Что называется
элементарным магнитным потоком? -
Что называется
магнитным потоком? -
При каких условиях
магнитный поток равен нулю? -
При каких условиях
магнитный поток равен произведению
индукции магнитного поля на площадь
контура? -
Сформулируйте
определение явления электромагнитной
индукции. -
Сформулируйте закон
электромагнитной индукции. -
Дайте определение
циркуляции магнитного поля. -
Запишите закон ЭМИ
в расшифрованном виде. -
Какое поле является
вихревым? -
Что такое ток Фуко?
-
Чем отличается
электрическое поле, созданное точечным
зарядом, от электрического поля,
появляющегося при ЭМИ? -
Сформулируйте закон
ЭМИ для замкнутого проводящего контура. -
При каких условиях
возникает ЭДС самоиндукции? -
Сформулируйте
определение явления самоиндукции. -
Сформулируйте
словами закон самоиндукции. -
Назовите все способы
создания переменного магнитного потока. -
Как изменяется со
временем магнитный поток в данной
работе? -
Как выглядит
поверхность, через которую формируется
переменный магнитный поток в данной
работе? -
Какова зависимость
магнитного потока от времени в данной
работе? -
Как направлен вектор
магнитной индукции в данной работе?
ЛАБОРАТОРНАЯ РАБОТА
2_6. Свободные колебания в контуре
Ознакомьтесь с теорией
в конспекте, учебнике (Савельев, т.2, §89,
§90). Запустите
программу «Эл-магн.Кванты». Выберите
«Электричество и магнетизм» и «Свободные
колебания в RLC контуре».
Нажмите вверху внутреннего окна кнопку
с изображением страницы. Прочитайте
краткие теоретические сведения.
Необходимое запишите в свой конспект.
(Если вы забыли, как работать с системой
компьютерного моделирования, прочитайте
ВВЕДЕНИЕ стр.5 еще раз).
ЦЕЛЬ РАБОТЫ:
-
Знакомство с
компьютерной моделью процесса свободных
затухающих колебаний в электрическом
колебательном контуре. -
Экспериментальное
исследование закономерностей свободных
затухающих колебаний. -
Экспериментальное
определение величины индуктивности
контура.
КРАТКАЯ ТЕОРИЯ:
КОЛЕБАТЕЛЬНЫМ КОНТУРОМ
называется замкнутая цепь, содержащая
катушку индуктивности с индуктивностью
L и конденсатор с емкостью С. Если в цепи
нет активного сопротивления R (резистора),
то в контуре возможны гармонические
(незатухающие) колебания тока I,
заряда конденсатора q и напряжения на
элементах.
НАПРЯЖЕНИЕ НА
КОНДЕНСАТОРЕ
.
ЭДС самоиндукции в
катушке
.
НАПРЯЖЕНИЕ НА РЕЗИСТОРЕ
.
ОПРЕДЕЛЕНИЕ ТОКА
.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ свободных
незатухающих колебаний
, где 0 =
— собственная
частота контура .
Период Т =
2
.
Его решение q(t) = qv
cos(0 t + ),
где — начальная
фаза.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ свободных
затухающих колебаний
,
где =
— коэффициент затухания.
Его решение q(t) = qv0
е—t
cos(t + ),
где
—
частота затухающих колебаний..
ПОСТОЯННАЯ ВРЕМЕНИ
ЗАТУХАНИЯ в контуре
есть время, за которое амплитуда колебаний
уменьшается в е = 2.73 раз. На графике
зависимости амплитуды затухающих
колебаний от времени касательная,
проведенная к этому графику в начальный
момент времени, пересекает ось времени
в точке t = .
q(t)
А1
А2 —- касательная
А3
t
t2=Т
t3=2Т
ЛОГАРИФМИЧЕСКИМ
ДЕКРЕМЕНТНОМ ЗАТУХАНИЯ называется
величина, определяемая формулой
.
ДОБРОТНОСТЬ контура равна Q =
.
МЕТОДИКА и ПОРЯДОК
ИЗМЕРЕНИЙ
Закройте окно теории.
Внимательно рассмотрите рисунок, найдите
все регуляторы и другие основные элементы
и зарисуйте их в конспект.

Получите у преподавателя допуск для
выполнения измерений.
ИЗМЕРЕНИЯ:
-
Нажмите мышью кнопку
«Выбор». Подведите маркер мыши к движку
регулятора, нажмите на левую кнопку
мыши и, удерживая ее в нажатом состоянии,
меняйте величину емкости конденсатора
и установите числовое значение, равное
взятому из таблицы 1 для вашей бригады.
Аналогичным способом установите
величину индуктивности в соответствии
с таблицей 1. -
Установите
сопротивления резистора R = 1 Ом. Нажав
кнопку «Старт», наблюдайте график
зависимости заряда конденсатора от
времени. Измерьте линейкой значения
первых шести амплитуд и запишите их в
таблицу 2. Меняя сопротивление R, повторите
измерения амплитуд и заполните таблицу
2.
ТАБЛИЦА 1. Значения емкости конденсатора
и индуктивности катушки (не перерисовывать)
|
Бригада |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
С [мкФ] |
3 |
3 |
2.7 |
2.7 |
2.4 |
2.4 |
2 |
2 |
|
L[мГн] |
6 |
7 |
8 |
9 |
10 |
9 |
8 |
7 |
ТАБЛИЦА
2. Результаты измерений при С = ____ мкФ, L
= ____ мГн,
Т =
____ мс.
|
R Ом |
А1 мм |
А2 мм |
А3 мм |
А4 мм |
А5 мм |
А6 мм |
мс |
с-1 |
|
1 |
||||||||
|
2 |
||||||||
|
3 |
||||||||
|
4 |
||||||||
|
5 |
||||||||
|
6 |
||||||||
|
t [мс] |
ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ
ОТЧЕТА:
-
Рассчитайте значения
периода колебаний и запишите в заголовке
табл. 2. -
Рассчитайте время
t , при котором измерена соответствующая
амплитуда и запишите в таблицу 2. -
Постройте на одном
чертеже графики экспериментальных
зависимостей амплитуды колебания А от
времени t (6 линий, соответствующих
разным R). -
Для каждого графика
постройте касательную к нему в начальный
момент времени. Продолжив касательную
до пересечения с осью времени, определите
экспериментальное значение постоянной
времени затухания ,
и запишите в таблицу 2. -
Рассчитайте величины
коэффициента затухания
= 1/ и также внесите
в таблицу 2. -
Постройте график
зависимости коэффициента затухания
от сопротивления резистора. -
По графику (
R ) определите индуктивность контура,
используя формулу
. -
Запишите ответ и
сформулируйте выводы по ответу и
графикам.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
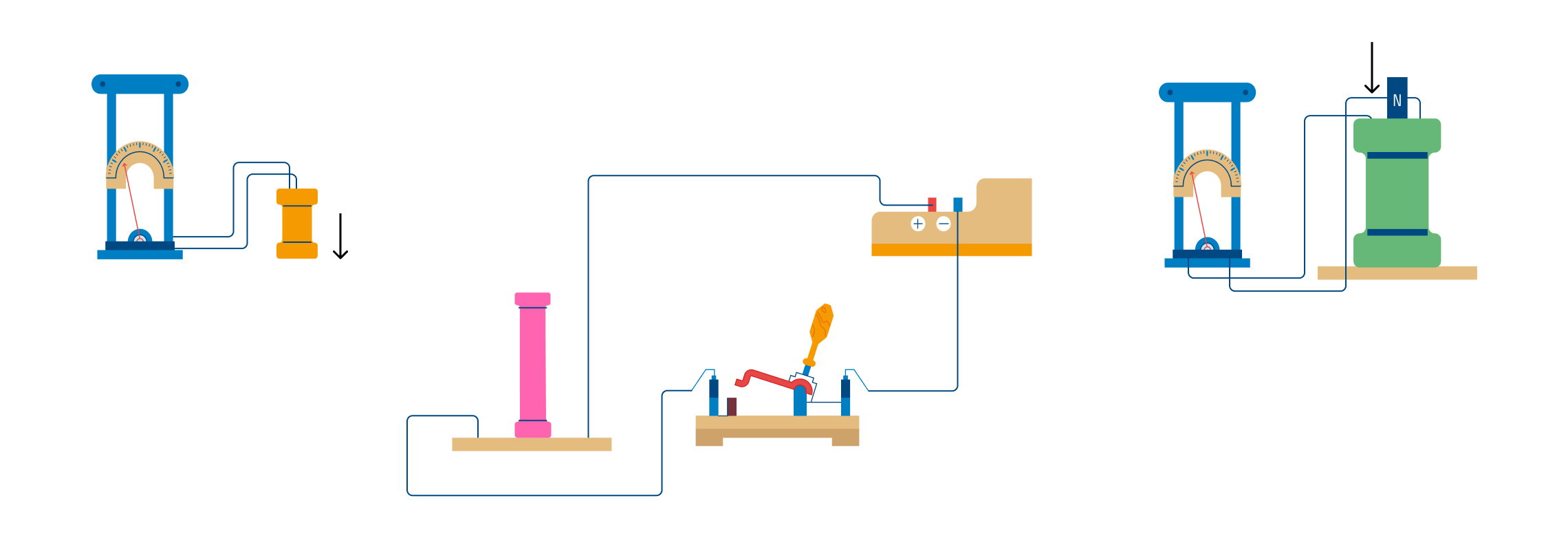
Рис. 5.1. Изменяющийся магнитный поток
1. Запустите эксперимент, щёлкнув мышью по кнопке «Старт». Наблюдайте движение перемычки и изменение магнитного потока Ф (цифры внизу окна).
2. Зацепив мышью, перемещайте движки регуляторов:
L – расстояния между проводами; R – сопротивления перемычки;
B1 – величины индукции магнитного поля.
Зафиксируйте значения, указанные в таблице 5.1 и под ней, для вашей бригады.
33
|
Таблица 5.1 |
||||
|
Значения характеристик (не перерисовывать) |
||||
|
Бригады |
R , Ом |
B1 , мТл |
B2 , мТл |
B3 , мТл |
|
1 и 5 |
1 |
1 |
40 |
90 |
|
2 и 6 |
2 |
2 |
20 |
80 |
|
3 и 7 |
1 |
1 |
10 |
70 |
|
4 и 8 |
2 |
2 |
-20 |
100 |
Для бригад 1–4 L = 1 м, для бригад 5–8 L = 0,7 м.
3. Установив указанное в таблице 5.2 значение скорости движе-ния перемычки, нажмите левую кнопку мыши, когда её маркер раз-мещён над кнопкой «Старт». Значения ЭДС и тока индукции занесите в таблицу 5.2. Повторите измерения для других значений скорости из таблицы 5.2.
|
Результаты измерений В = ____ мТл |
Таблица 5.2 |
|||||||||||||
|
V , м/c |
-10 |
-8 |
-6 |
-4 |
-2 |
0 |
2 |
4 |
6 |
8 |
10 |
|||
|
ЭДС, В |
||||||||||||||
|
I , мА |
4. Повторите измерения для двух других значений индукции магнитного поля, выбирая их из таблицы 5.1. Полученные результаты запишите в таблицы 5.3 и 5.4.
Таблица 5.3
Результаты измерений В = ____ мТл
|
V , м/c |
-10 |
-8 |
-6 |
-4 |
-2 |
0 |
2 |
4 |
6 |
8 |
10 |
|
ЭДС, В |
|||||||||||
|
I , мА |
|
Результаты измерений В = ____ мТл |
Таблица 5.4 |
|||||||||||||
|
V , м/c |
-10 |
-8 |
-6 |
-4 |
-2 |
0 |
2 |
4 |
6 |
8 |
10 |
|||
|
ЭДС, В |
||||||||||||||
|
I , мА |
Обработка данных и анализ результатов
1. Постройте на одном листе графики зависимости тока индук-ции от скорости движения перемычки при трёх значениях индукции магнитного поля.
34
2. Для каждой прямой определите тангенс угла наклона по фор-
|
муле: tg( )ЭКСП |
I |
. |
||||
|
V |
||||||
|
3. Вычислите теоретическое значение тангенса для каждой пря- |
||||||
|
мой по формуле: tg( )ТЕОР |
BL . |
|||||
|
R |
||||||
|
4. Заполните таблицу 5.4 результатов измерений. |
||||||
|
Результаты измерений |
Таблица 5.4 |
|||||
|
Номер измерения |
tg( )ЭКСП, Ac/м |
tg( )ТЕОР, Ac/м |
||||
5. Сделайте выводы по графикам и результатам измерений.
Контрольные вопросы
1. Что называется элементарным магнитным потоком?
2. Что называется магнитным потоком?
3. При каких условиях магнитный поток равен нулю?
4. При каких условиях магнитный поток равен произведению индукции магнитного поля на площадь контура?
5. Сформулируйте определение явления электромагнитной ин-дукции.
6. Сформулируйте закон электромагнитной индукции.
7. Дайте определение циркуляции магнитного поля.
8. Запишите закон электромагнитной индукции в расшифрован-ном виде.
9. Какое поле является вихревым?
10. Что такое ток Фуко?
11. Чем отличается электрическое поле, созданное точечным за-рядом, от электрического поля, появляющегося при электро-магнитной индукции?
12. Сформулируйте закон электромагнитной индукции для замк-нутого проводящего контура.
13. При каких условиях возникает ЭДС самоиндукции?
14. Сформулируйте определение явления самоиндукции.
35
15. Сформулируйте словами закон самоиндукции.
16. Назовите все способы создания переменного магнитного по-тока.
17. Как изменяется со временем магнитный поток в данной рабо-те?
18. Как выглядит поверхность, через которую формируется пе-ременный магнитный поток в данной работе?
19. Какова зависимость магнитного потока от времени в данной работе?
20. Как направлен вектор магнитной индукции в данной работе?
Лабораторная работа № 6 СВОБОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ
Выберите «Электричество и магнетизм» и «Свободные колеба-ния в RLC-контуре». Нажмите вверху внутреннего окна кнопку с изо-бражением страницы.
Цель работы:
знакомство с компьютерной моделью процесса свободных за-тухающих колебаний в электрическом колебательном контуре; экспериментальное исследование закономерностей свобод —
ных затухающих колебаний; экспериментальное определение величины индуктивности
контура.
Краткие сведения из теории
Колебательным контуром называется замкнутая цепь, содержа-щая катушку индуктивности с индуктивностью L и конденсатор ём-костью C . Если в цепи нет активного сопротивления R (резистора), то в контуре возможны гармонические (незатухающие) колебания то-ка I , заряда конденсатора q и напряжения на элементах.
Напряжение на конденсаторе Uc Cq .
ЭДС самоиндукции в катушке L dIdt . Напряжение на резисторе U R IR .
36
|
Определение тока I dq . |
|||||||||||||||
|
dt |
|||||||||||||||
|
Дифференциальное уравнение свободных незатухающих коле- |
|||||||||||||||
|
баний: |
d 2q 02q 0 , |
||||||||||||||
|
1 |
dt 2 |
||||||||||||||
|
где |
– собственная частота контура. Период Т 2 LC . |
||||||||||||||
|
0 |
LC |
||||||||||||||
|
Решение уравнения свободных незатухающих колебаний имеет |
|||||||||||||||
|
вид: |
q(t) q |
cos( t ) , |
|||||||||||||
|
где – начальная фаза. |
0 |
0 |
|||||||||||||
|
Дифференциальное уравнение свободных затухающих колеба- |
|||||||||||||||
|
ний: |
d 2q |
dq |
|||||||||||||
|
2 |
2 |
||||||||||||||
|
q 0 , |
|||||||||||||||
|
dt2 |
dt |
0 |
|||||||||||||
|
R |
|||||||||||||||
|
где |
– коэффициент затухания. |
||||||||||||||
|
2L |
|||||||||||||||
|
Решение уравнения свободных затухающих колебаний имеет |
|||||||||||||||
|
вид: |
q(t) q e— t cos( t ) , |
||||||||||||||
|
0 |
|||||||||||||||
|
где |
2 |
2 |
– частота затухающих колебаний. |
||||||||||||
|
0 |
|||||||||||||||
|
Период свободных затухающих колебаний: |
|||||||||||||||
|
T |
2 |
. |
|||||||||||||
|
2 |
2 |
||||||||||||||
|
0 |

которое амплитуда колебаний уменьшается в e раз ( e 2,73). Логарифмическим декрементом затухания называется величина,
|
определяемая формулой ln |
q(t) |
T T . |
|
|
q(t T ) |
|||
|
Добротность контура равна Q |
. |
||
Методика и порядок измерений
Внимательно рассмотрите рисунок 6.1, найдите все регуляторы и другие основные элементы и зарисуйте их в конспект.
37
Рис. 6.1. Изменяющийся магнитный поток
Нажмите мышью кнопку «Выбор». Подведите маркер мыши к движку регулятора, нажмите на левую кнопку мыши и, удерживая её в нажатом состоянии, меняйте величину ёмкости конденсатора С и установите числовое значение, равное взятому из таблицы 6.1, для вашей бригады. Аналогичным способом установите величину индук-тивности L в соответствии с таблицей 6.1.
Таблица 6.1
Значения ёмкости конденсатора и индуктивности катушки (не перерисовывать)
|
Бригада |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
C , мкФ |
3 |
3 |
2,7 |
2,7 |
2,4 |
2,4 |
2 |
2 |
|
L , мГн |
6 |
7 |
8 |
9 |
10 |
9 |
8 |
7 |
Установите сопротивления резистора R 1 Ом. Нажав кнопку «Старт», наблюдайте график зависимости заряда конденсатора от времени. Измерьте линейкой значения первых шести амплитуд коле-бания заряда A и запишите их в таблицу 6.2. Меняя сопротивление R , повторите измерения амплитуд и заполните таблицу 6.2.
38
Таблица 6.2
Результаты измерений при С = ___ мкФ, L = ___ мГн, Т = ___ мс
|
R , Ом |
A1 , Кл |
A2 , Кл |
A3 , Кл |
A4 , Кл |
A5 , Кл |
A6 , Кл |
, мс |
, с-1 |
|
1 |
||||||||
|
2 |
||||||||
|
3 |
||||||||
|
4 |
||||||||
|
5 |
||||||||
|
6 |
||||||||
|
t, мс |
Обработка данных и анализ результатов
1. Рассчитайте значения периода колебаний T и запишите в за-головке таблицы 6.2.
2. Рассчитайте время t , при котором измерена соответствующая амплитуда колебания заряда A , и запишите в таблицу 6.2.
3. Постройте на одном чертеже графики экспериментальных за —
висимостей амплитуды колебания заряда А от времени t (6 линий, соответствующих разным R ).
4. Для каждого графика постройте касательную к нему в на-чальный момент времени. Продолжив касательную до пересе-чения с осью времени, определите экспериментальное значе-ние постоянной времени затухания и запишите в таблицу 6.2.
5. Рассчитайте величины коэффициента затухания 1 и также
внесите в таблицу 6.2.
6. Постройте график зависимости коэффициента затухания от сопротивления резистора R .
7. По графику f (R) определите индуктивность контура L ,
используя формулу L 1 R .
2
8. Запишите ответ и сформулируйте выводы по ответу и графи-кам.
ЭЛЕМЕНТАРНЫМ МАГНИТНЫМ ПОТОКОМ dФB через физически малый элемент поверхности площадью dS называется скалярное произведение вектора индукции магнитного поля 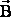
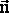
dФB = (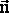
МАГНИТНЫМ ПОТОКОМ ФB через поверхность площадью S называется сумма всех элементарных потоков через все элементы этой поверхности (интеграл по поверхности):
ФB = 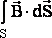
Анализируя свойства интеграла в правой части данного соотношения, можем получить условия, когда для определения потока не требуется интегрирование.
Простейший вариант: потока нет (ФВ = 0), если 1) В = 0 или 2) вектор магнитной индукции направлен по касательной к поверхности в любой ее точке (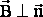
Второй вариант: поток есть произведение индукции на площадь (ФВ = B?S), если 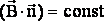
ИНДУКЦИЕЙ называется явление возникновения одного поля (например, электрического) при изменении другого поля (например, магнитного).
ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИЕЙ называется явление возникновения электрического поля при изменении магнитного поля.
ЗАКОН ЭМИ: циркуляция электрического поля по замкнутому контуру Г0Е пропорциональна быстроте изменения потока магнитного поля Ф0В через замкнутую поверхность S0 (L0), ограниченную контуром L0 , по которому рассчитана циркуляция. Математически:
Г0Е = —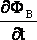
В расшифрованном виде 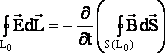
В результате ЭМИ возникает электрическое поле с ненулевой циркуляцией. Поле с ненулевой циркуляцией называется вихревым.
Если в таком поле находится проводящее вещество, то в веществе возникает ВИХРЕВОЙ ЭЛЕКТРИЧЕСКИЙ ТОК, величина которого пропорциональна напряженности вихревого электрического поля. Такие токи называются токами Фуко.
Если проводящее вещество имеет форму ЗАМКНУТОГО КОНТУРА, тогда циркуляция электрического поля в нем определяет ЭДС, которая в случае ЭМИ называется ЭДС индукции. Закон ЭМИ для проводящего контура будет выглядеть так ЭДСИНД = —
Ток, который в этом случае появляется в контуре, называется индукционным.
Обозначая ЭДС индукции символом eинд и используя закон Ома для полной цепи, получим выражение для тока индукции iИНД = eинд / R , где R – сопротивление контура.
Если имеется замкнутый контур с переменным током, тогда магнитное поле с изменяющимся потоком создается собственным током в этом контуре, и в соответствии с законом ЭМИ в контуре возникает дополнительная ЭДС, называемая ЭДС самоиндукции.
Явлением САМОИНДУКЦИИ называется возникновение ЭДС самоиндукции при протекании по проводнику переменного тока.
ЗАКОН самоиндукции: ЭДССАМОИНД = -L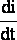
МЕТОДИКА и ПОРЯДОК ИЗМЕРЕНИЙ
Закройте окно теории.
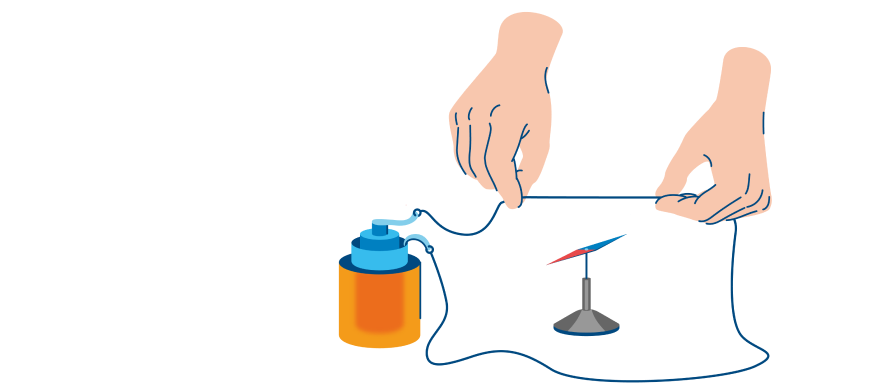
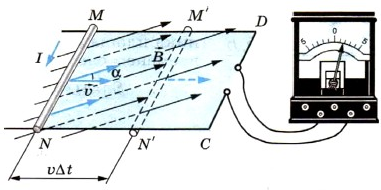
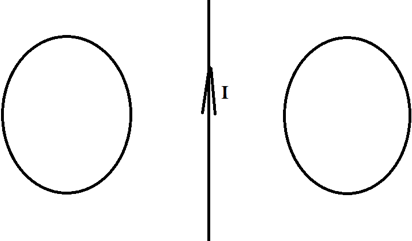
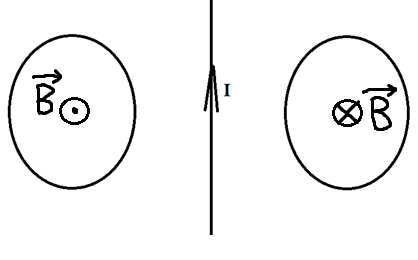
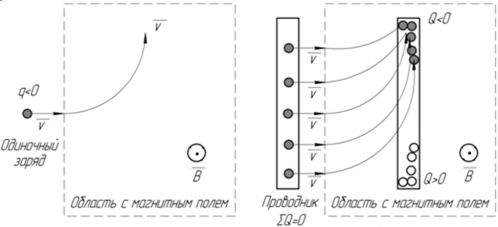
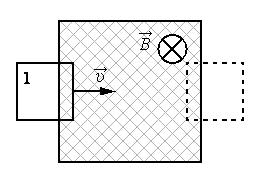
В данной лабораторной работе используется компьютерная модель, в которой изменяющийся магнитный поток возникает в результате движения проводящей перемычки по параллельным проводникам, замкнутым с одной стороны.
Эта система изображена на рисунке:
ЗАДАЧА:
Проводящая перемычка движется со скоростью V по параллельным проводам, замкнутым с одной стороны. Система проводников расположена в однородном магнитном поле, индукция которого равна В и направлена перпендикулярно плоскости, в которой расположены проводники. Найти ток в перемычке, если ее сопротивление R, а сопротивлением проводников можно пренебречь.
Решив задачу в черновике, получите уравнение для тока в общем виде.
Подготовьте таблицу 1, используя образец. Подготовьте также таблицы 3 и 4, аналогичные табл.1.
|
ТАБЛИЦА 1. РЕЗУЛЬТАТЫ ИЗМЕРЕНИЙ (12 столбцов). В = ____ мТл |
ТАБЛИЦА 2. Значения характеристик (не перерисовывать) |
||||||||||||
|
v (м/c) = |
-10 |
-8 |
… |
10 |
Варианты |
R (Ом) |
В1 (мТл) |
В2 (мТл) |
В3 (мТл) |
||||
|
ЭДС, В |
1 и 5 |
1 |
-30 |
40 |
90 |
||||||||
|
I, мА |
2 и 6 |
2 |
-40 |
20 |
80 |
||||||||
|
3 и 7 |
1 |
-50 |
10 |
70 |
|||||||||
|
4 и 8 |
2 |
-60 |
-20 |
100 |
|||||||||
Для вариантов 1-4 L = 1 м, для вариантов 5-8 L = 0.7 м.
ИЗМЕРЕНИЯ:
1. Закройте окно теории (если вы ее вызывали), нажав кнопку в правом верхнем углу внутреннего окна. Запустите эксперимент, щелкнув мышью по кнопке «Старт». Наблюдайте движение перемычки и изменение магнитного потока Ф (цифры внизу окна) .
2. Зацепив мышью, перемещайте движки регуляторов
· L –расстояния между проводами,
· R – сопротивления перемычки,
· В1 – величины индукции магнитного поля
и зафиксируйте значения, указанные в таблице 2 и под ней для вашего варианта.
3. Установив указанное в табл.1 значение скорости движения перемычки, нажмите левую кнопку мыши, когда ее маркер размещен над кнопкой «Старт». Значения ЭДС и тока индукции занесите в табл.1. Повторите измерения для других значений скорости из табл.1.
4. Повторите измерения для двух других значений индукции магнитного поля, выбирая их из табл.2. Полученные результаты запишите в табл.3 и 4.
ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЕТА
1. Постройте на одном листе графики зависимости тока индукции от скорости движения перемычки при трех значениях индукции магнитного поля.
2. Для каждой прямой определите тангенс угла наклона по формуле
tg(j) = 
3. Вычислите теоретическое значение тангенса для каждой прямой по формуле tg(j)ТЕОР = 
4. Заполните таблицу результатов измерений
|
Номер измерения |
tg(j)ЭКСП (Ac/м) |
tg(j)ТЕОР (Ac/м) |
5. Сделайте выводы по графикам и результатам измерений.
- Что называется элементарным магнитным потоком?
- Что называется магнитным потоком?
- При каких условиях магнитный поток равен нулю?
- При каких условиях магнитный поток равен произведению индукции магнитного поля на площадь контура?
- Сформулируйте определение явления электромагнитной индукции.
- Сформулируйте закон электромагнитной индукции.
- Дайте определение циркуляции магнитного поля.
- Запишите закон ЭМИ в расшифрованном виде.
- Какое поле является вихревым?
- Что такое ток Фуко?
- Чем отличается электрическое поле, созданное точечным зарядом, от электрического поля, появляющегося при ЭМИ?
- Сформулируйте закон ЭМИ для замкнутого проводящего контура.
- При каких условиях возникает ЭДС самоиндукции?
- Сформулируйте определение явления самоиндукции.
- Сформулируйте словами закон самоиндукции.
- Назовите все способы создания переменного магнитного потока.
- Как изменяется со временем магнитный поток в данной работе?
- Как выглядит поверхность, через которую формируется переменный магнитный поток в данной работе?
- Какова зависимость магнитного потока от времени в данной работе?
- Как направлен вектор магнитной индукции в данной работе?
 |
Введение |  |
 |
Цель работы |  |
 |
Краткая теория |  |
 |
Модель |  |
 |
Методика и порядок измерений |  |
 |
Измерения |  |
 |
Обработка результатов и оформление отчета |  |
 |
Вопросы и задания для самоконтроля |  |
 |
Литература |  |
Закон электромагнитной индукции
О чем эта статья:
11 класс, ЕГЭ/ОГЭ
Магнитный поток
Прежде, чем разобраться с тем, что такое электромагнитная индукция, нужно определить такую сущность, как магнитный поток.
Представьте, что вы взяли обруч в руки и вышли на улицу в ливень. Чем сильнее ливень, тем больше через этот обруч пройдет воды — поток воды больше.
Если обруч расположен горизонтально, то через него пройдет много воды. А если начать его поворачивать — уже меньше, потому что он расположен не под прямым углом к вертикали.
Теперь давайте поставим обруч вертикально — ни одной капли не пройдет сквозь него (если ветер не подует, конечно).
Магнитный поток по сути своей — это тот же самый поток воды через обруч, только считаем мы величину прошедшего через площадь магнитного поля, а не дождя.
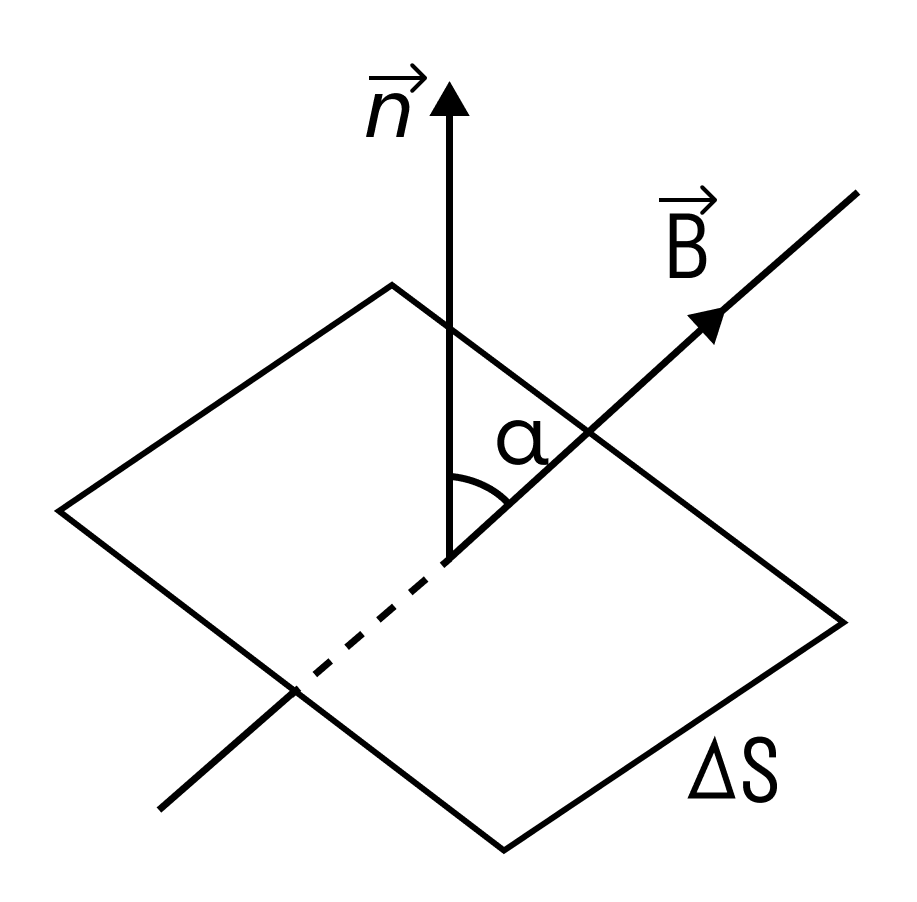
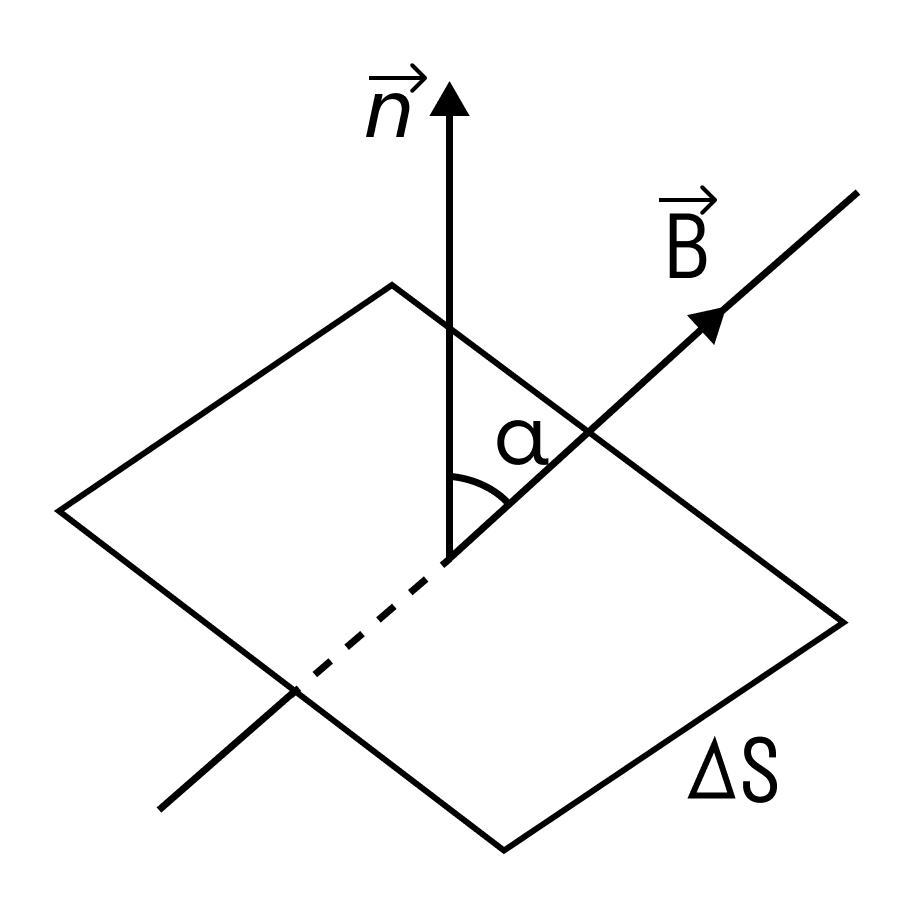
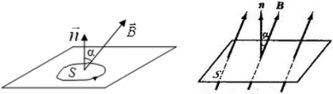
Магнитным потоком через площадь S контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции B, площади поверхности S, пронизываемой данным потоком, и косинуса угла α между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):
Магнитный поток
Ф — магнитный поток [Вб]
B — магнитная индукция [Тл]
S — площадь пронизываемой поверхности [м^2]
n — вектор нормали (перпендикуляр к поверхности) [-]
Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла α магнитный поток может быть положительным (α 90°). Если α = 90°, то магнитный поток равен 0. Это зависит от величины косинуса угла.
Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура, магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Электромагнитная индукция
Электромагнитная индукция — явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
Майкл Фарадей провел ряд опытов, которые помогли открыть явление электромагнитной индукции.
Опыт раз. На одну непроводящую основу намотали две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй — подключены к источнику тока.
При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
Опыт два. Первую катушку подключили к источнику тока, а вторую — к гальванометру. При этом вторая катушка перемещалась относительно первой. При приближении или удалении катушки фиксировался ток.
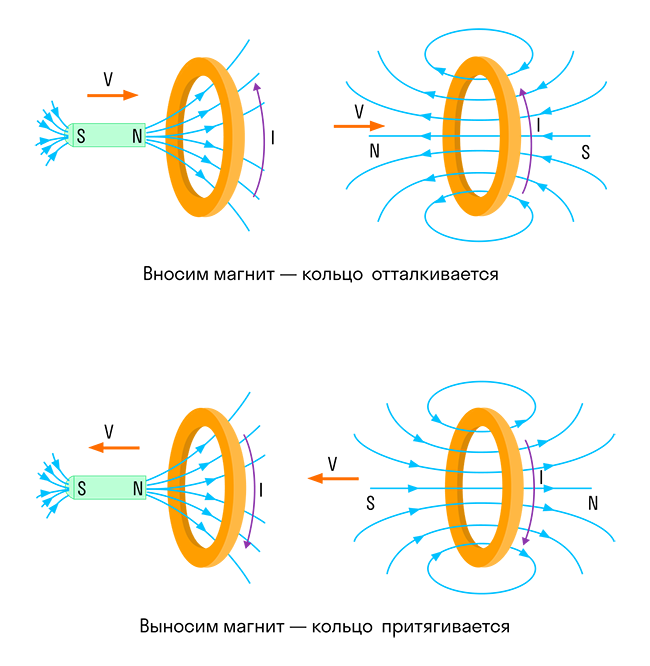
Опыт три. Катушка замкнута на гальванометр, а магнит движется вдвигается (выдвигается) относительно катушки
Вот, что показали эти опыты:
- Индукционный ток возникает только при изменении линий магнитной индукции.
- Направление тока будет различно при увеличении числа линий и при их уменьшении.
- Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Почему возникает индукционный ток?
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС.
Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
Закон электромагнитной индукции
Закон электромагнитной индукции (закон Фарадея) звучит так:
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром.
Математически его можно описать формулой:
Закон Фарадея
Ɛi — ЭДС индукции [В]
ΔФ/Δt — скорость изменения магнитного потока [Вб/с]
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре всегда направлен так, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из N витков (то есть он — катушка), то ЭДС индукции будет вычисляться следующим образом.
Закон Фарадея для контура из N витков
Ɛi — ЭДС индукции [В]
ΔФ/Δt — скорость изменения магнитного потока [Вб/с]
N — количество витков [-]
Сила индукционного тока в замкнутом проводящем контуре с сопротивлением R:
Закон Ома для проводящего контура
Ɛi — ЭДС индукции [В]
I — сила индукционного тока [А]
R — сопротивление контура [Ом]
Если проводник длиной l будет двигаться со скоростью v в постоянном однородном магнитном поле с индукцией B ЭДС электромагнитной индукции равна:
ЭДС индукции для движущегося проводника
Ɛi — ЭДС индукции [В]
B — магнитная индукция [Тл]
v — скорость проводника [м/с]
l — длина проводника [м]
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле
- вследствие изменения во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Правило Ленца
Чтобы определить направление индукционного тока, нужно воспользоваться правилом Ленца.
Академически это правило звучит следующим образом: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Давайте попробуем чуть проще: катушка в данном случае — это недовольная бабуля. Забирают у нее магнитный поток — она недовольна и создает магнитное поле, которое этот магнитный поток хочет обратно отобрать.
Дают ей магнитный поток, забирай, мол, пользуйся, а она такая — «Да зачем сдался мне ваш магнитный поток!» и создает магнитное поле, которое этот магнитный поток выгоняет.
Электромагнитная индукция
Явление электромагнитной индукции
Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
- На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
- Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
- Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.
Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.
Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Объяснения возникновения индукционного тока
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.
Свойства вихревого электрического поля:
- источник – переменное магнитное поле;
- обнаруживается по действию на заряд;
- не является потенциальным;
- линии поля замкнутые.
Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.
Магнитный поток
Магнитным потоком через площадь ( S ) контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ( B ) , площади поверхности ( S ) , пронизываемой данным потоком, и косинуса угла ( alpha ) между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):
Обозначение – ( Phi ) , единица измерения в СИ – вебер (Вб).
Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м 2 , расположенную перпендикулярно вектору магнитной индукции:
Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла ( alpha ) магнитный поток может быть положительным ( ( alpha ) ( alpha ) > 90°). Если ( alpha ) = 90°, то магнитный поток равен 0.
Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Закон электромагнитной индукции Фарадея
Закон электромагнитной индукции (закон Фарадея):
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из ( N ) витков, то ЭДС индукции:
Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ( R ) :
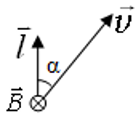
При движении проводника длиной ( l ) со скоростью ( v ) в постоянном однородном магнитном поле с индукцией ( vec ) ЭДС электромагнитной индукции равна:
где ( alpha ) – угол между векторами ( vec ) и ( vec ) .
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
- вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Правило Ленца
Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Алгоритм решения задач с использованием правила Ленца:
- определить направление линий магнитной индукции внешнего магнитного поля;
- выяснить, как изменяется магнитный поток;
- определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
- по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.
Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
Самоиндукция
Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.
При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.
В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.
Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.
При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.
Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.
Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.
При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.
ЭДС самоиндукции ( varepsilon_ ) , возникающая в катушке с индуктивностью ( L ) , по закону электромагнитной индукции равна:
ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.
Индуктивность
Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток ( Phi ) через контур из этого проводника пропорционален модулю индукции ( vec ) магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.
Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:
Индуктивность – коэффициент пропорциональности ( L ) между силой тока ( I ) в контуре и магнитным потоком ( Phi ) , создаваемым этим током:
Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.
Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:
Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.
Энергия магнитного поля
При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.
Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:
Основные формулы раздела «Электромагнитная индукция»
Алгоритм решения задач по теме «Электромагнитная индукция»:
1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.
2. Записать формулу:
- закона электромагнитной индукции;
- ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.
3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.
4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).
5. Решить полученную систему уравнений относительно искомой величины.
Закон электромагнитной индукции
теория по физике 🧲 магнетизм
Магнитный поток наглядно истолковывается как число линий магнитной индукции, пронизывающих поверхность площадью S. Поэтому скорость изменения этого числа есть не что иное, как скорость изменения магнитного потока.
Если за малое время ∆t магнитный поток поменялся на ∆Ф, то скорость изменения магнитного потока равна Δ Φ Δ t . . . Поэтому утверждение, которое вытекает непосредственно из опыта, можно сформулировать так:
Сила индукционного тока пропорциональная скорости изменения магнитного потока через поверхность, ограниченную контуром:
Известно, что в цепи появляется электрический ток в том случае, когда на свободные заряды проводника действуют сторонние силы. Работу этих сил при перемещении единичного положительного заряда вдоль замкнутого контура называют электродвижущей силой. Следовательно, при изменении магнитного потока через поверхность, ограниченную контуров, появляются сторонние силы, действие которых характеризуется ЭДС, называемой ЭДС индукции. Обозначают ее как ε i .
Согласно закону Ома для замкнутой цепи:
Сопротивление проводника не зависит от изменения магнитного потока. Следовательно, сила индукционного тока пропорциональна скорости изменения магнитного потока только потому, что ЭДС индукции тоже пропорциональна этой скорости изменения потока.
Закон электромагнитной индукции
ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром.
ε i = ∣ ∣ ∣ Δ Φ Δ t . . ∣ ∣ ∣
Закон электромагнитной индукции формулируется именно для ЭДС, а не для силы тока. При такой формулировке закон выражает сущность явления, не зависящую от свойств проводников, в которых возникает индукционный ток.
Определение знака ЭДС индукции
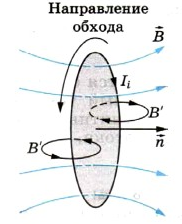
На рисунке изображен замкнутый контур. Будем считать положительным направление обхода контура против часовой стрелки. Нормаль → n к контуру образует правый винт с направлением обхода.
Пусть магнитная индукция → B внешнего магнитного поля направлена вдоль нормали к контуру и возрастает со временем. Тогда Φ > 0 и Δ Φ Δ t . . > 0 . Согласно правилу Ленца индукционный ток создает магнитный поток Φ ‘ 0 . Линии магнитной индукции B’ магнитного поля индукционного тока изображены черным цветом. Следовательно, индукционный ток Ii согласно правилу буравчика направлен по часовой стрелке (против направления положительного обхода) и ЭДС индукции отрицательна. Поэтому в законе электромагнитной индукции должен стоять знак «–», указывающий на то, что ε i и Δ Φ Δ t . . имеют разные знаки:
Пример №1. Магнитный поток через контур проводника сопротивлением 3∙10 –2 Ом за 2 с изменился на 1,2∙10 –2 Вб. Найдите силу тока в проводнике, если изменение потока происходило равномерно.
ε i = ∣ ∣ ∣ Δ Φ Δ t . . ∣ ∣ ∣
ЭДС индукции в движущихся проводниках
Электроны в неподвижном проводнике приводятся в движение электрическим полем, и это поле порождается переменным магнитным полем. Следовательно, изменяясь во времени, магнитное поле порождает электрическое поле. Но если проводник движется в постоянном во времени магнитном поле, то ЭДС индукции в проводнике обусловлена не вихревым электрическим полем, которое в этом случае не может возникнуть, а другой причиной.
При движении проводника его свободные заряды движутся вместе с ним. Поэтому на заряды со стороны магнитного поля действует сила Лоренца. Она и вызывает перемещение зарядов внутри проводника. ЭДС индукции, следовательно, имеет магнитное происхождение.
Вычислим ЭДС индукции, возникающую в проводнике, движущемся в однородном магнитном поле (см. рисунок). Пусть сторона контура MN длиной l скользит с постоянной скоростью → v вдоль сторон NC и MD, оставаясь все это время параллельной стороне CD. Вектор магнитной индукции → B однородного поля перпендикулярен проводнику и составляет угол α с направлением его скорости.
Сила, с которой магнитное поле действует на движущуюся заряженную частицу, равна по модулю:
F L = | q | v B sin . α
Направлена эта сила вдоль проводника MN. Работа силы Лоренца на пути l положительна и составляет:
A = F L l = | q | v B l sin . α
Формула выше определяет неполную работу силы Лоренца. Кроме силы Лоренца имеется составляющая силы Лоренца, направленная против скорости проводника → v . Такая составляющая тормозит проводник и совершает отрицательную работу. В результате полная работа силы Лоренца оказывается равной нулю.
Электродвижущая сила индукции в проводнике MN равна по определению отношению работы по перемещению заряда q к этому заряду:
ε i = A | q | . . = v B l sin . α
Эта формула справедлива для любого проводника длиной l, движущегося со скоростью → v в однородном магнитном поле.
В других проводниках контура ЭДС равна нулю, так как проводники неподвижны. Следовательно, ЭДС во всем контуре MNCD равна ε i и остается неизменной, если скорость движения → v постоянна. Электрический ток при этом будет увеличиваться, так как при смещении проводника MN вправо уменьшается общее сопротивление контура.
С другой стороны, ЭДС индукции можно вычислить с помощью закона электромагнитной индукции. Магнитный поток через контур MNCD равен:
Φ = B S cos . ( 90 ° − α ) = B S sin . α
угол 90 ° − α представляет собой угол между векторами → B и нормалью → n к поверхности контура, а S — площадь контура MNCD. Если считать, что в начальный момент времени t=0 проводник MN находится на расстоянии NC от проводника CD, то при перемещении проводника площадь S изменяется со временем следующим образом:
За время ∆t площадь контура меняется на Δ S = − l v Δ t . Знак «минус» указывает на то, что она уменьшается. Изменение магнитного потока за это время равно:
Δ Φ = − B v l Δ t sin . α
ε i = − Δ Φ Δ t . . = B v l sin . α
Если весь контур MNCD движется в однородном магнитном поле, сохраняя свою ориентацию по отношению к вектору → B , то ЭДС индукции в контуре будет равна нулю, так как поток Φ через поверхность, ограниченную контуром, не меняется. Объяснить это можно так. При движении контура в проводниках MN и CD возникают силы, действующие на электроны в направлениях от N к M и от C к D. Суммарная работа этих сил при обходе контура по часовой стрелке или против нее равна нулю.
Пример №2. Проводник длиной 50 см движется в однородном магнитном поле со скоростью 4 м/с перпендикулярно силовым линиям. Найдите разность потенциалов, возникающую на концах проводника, если вектор магнитной индукции 8 мТл.
8 мТл = 8∙10 –3 Тл
Так как проводник движется перпендикулярно силовым линиям, то угол α равен 90 градусам, а синус прямого угла равен единице. Поэтому:
ε i = B v l sin . α = 8 · 10 − 3 · 4 · 0 , 5 · 1 = 16 · 10 − 3 ( В )
источники:
http://fizi4ka.ru/egje-2018-po-fizike/jelektromagnitnaja-indukcija.html
http://spadilo.ru/zakon-elektromagnitnoj-indukcii/
Магнитный поток
Прежде, чем разобраться с тем, что такое электромагнитная индукция, нужно определить такую сущность, как магнитный поток.
Представьте, что вы взяли обруч в руки и вышли на улицу в ливень. Чем сильнее ливень, тем больше через этот обруч пройдет воды — поток воды больше.
Если обруч расположен горизонтально, то через него пройдет много воды. А если начать его поворачивать — уже меньше, потому что он расположен не под прямым углом к вертикали.
Теперь давайте поставим обруч вертикально — ни одной капли не пройдет сквозь него (если ветер не подует, конечно).
Магнитный поток по сути своей — это тот же самый поток воды через обруч, только считаем мы величину прошедшего через площадь магнитного поля, а не дождя.
Магнитным потоком через площадь S контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции B, площади поверхности S, пронизываемой данным потоком, и косинуса угла α между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):
Магнитный поток
Ф — магнитный поток [Вб]
B — магнитная индукция [Тл]
S — площадь пронизываемой поверхности [м^2]
n — вектор нормали (перпендикуляр к поверхности) [-]
Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла α магнитный поток может быть положительным (α < 90°) или отрицательным (α > 90°). Если α = 90°, то магнитный поток равен 0. Это зависит от величины косинуса угла.
Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура, магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Пятерка по физике у тебя в кармане!
Решай домашку по физике на изи. Подробные решения помогут разобраться в сложной теме и получить пятерку!
Электромагнитная индукция
Электромагнитная индукция — явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
Майкл Фарадей провел ряд опытов, которые помогли открыть явление электромагнитной индукции.
Опыт раз. На одну непроводящую основу намотали две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй — подключены к источнику тока.
При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
Опыт два. Первую катушку подключили к источнику тока, а вторую — к гальванометру. При этом вторая катушка перемещалась относительно первой. При приближении или удалении катушки фиксировался ток.
Опыт три. Катушка замкнута на гальванометр, а магнит движется вдвигается (выдвигается) относительно катушки
Вот, что показали эти опыты:
- Индукционный ток возникает только при изменении линий магнитной индукции.
- Направление тока будет различно при увеличении числа линий и при их уменьшении.
- Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Почему возникает индукционный ток?
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС.
Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
Закон электромагнитной индукции
Закон электромагнитной индукции (закон Фарадея) звучит так:
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром.
Математически его можно описать формулой:
Закон Фарадея
Ɛi — ЭДС индукции [В]
ΔФ/Δt — скорость изменения магнитного потока [Вб/с]
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре всегда направлен так, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из N витков (то есть он — катушка), то ЭДС индукции будет вычисляться следующим образом.
Закон Фарадея для контура из N витков
Ɛi — ЭДС индукции [В]
ΔФ/Δt — скорость изменения магнитного потока [Вб/с]
N — количество витков [-]
Сила индукционного тока в замкнутом проводящем контуре с сопротивлением R:
Закон Ома для проводящего контура
Ɛi — ЭДС индукции [В]
I — сила индукционного тока [А]
R — сопротивление контура [Ом]
Если проводник длиной l будет двигаться со скоростью v в постоянном однородном магнитном поле с индукцией B ЭДС электромагнитной индукции равна:
ЭДС индукции для движущегося проводника
Ɛi — ЭДС индукции [В]
B — магнитная индукция [Тл]
v — скорость проводника [м/с]
l — длина проводника [м]
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле
- вследствие изменения во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Правило Ленца
Чтобы определить направление индукционного тока, нужно воспользоваться правилом Ленца.
Академически это правило звучит следующим образом: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Давайте попробуем чуть проще: катушка в данном случае — это недовольная бабуля. Забирают у нее магнитный поток — она недовольна и создает магнитное поле, которое этот магнитный поток хочет обратно отобрать.
Дают ей магнитный поток, забирай, мол, пользуйся, а она такая — «Да зачем сдался мне ваш магнитный поток!» и создает магнитное поле, которое этот магнитный поток выгоняет.
Магнитный поток, проходящий через площадь S равен:
Ф = BScosα;
где:
Ф ― величина магнитного потока [Вб],
S ― площадь контура [м2],
B ― индукция магнитного поля [Тл],
α ― угол между нормалью $overrightarrow{n}$ к площади контура и вектором индукции магнитного поля $overrightarrow{B}$.
Если вектор индукции магнитного поля $overrightarrow{B}$ перпендикулярен площади контура, то магнитный поток равен:
Ф = BScos90° = BS;
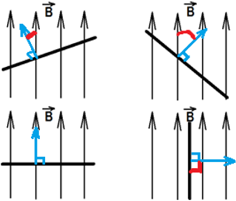
Максимальное значение потока будет тогда, когда косинус будет максимальным (cosα = 1), то есть угол между вектором $overrightarrow{B}$ и вектором нормали к пластинке равен 0°, чему соответствует картинка 3. Наименьшее же значение потока будет тогда, когда косинус будет равен нулю (cosα = 0), то есть угол между нормалью к пластинке и вектором индукции равен 90°, чему соответствует картинка 4.
Электромагнитная индукция ― явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через контур. Если контур разомкнут, то на его концах наблюдается разносность потенциалов, равная ЭДС индукции.
ЭДС электромагнитной индукции возникает только тогда, когда изменяется магнитный поток.
Закон Фарадея об электромагнитной индукции и гласит, что индуцируемая ЭДС прямо пропорциональна скорости изменения магнитного потока:
$varepsilon_i = -frac{Delta text{Ф}}{Delta t}$
где:
$varepsilon_i $ ― ЭДС электромагнитной индукции [B],
$frac{Delta text{Ф}}{Delta t}$ ― скорость изменения магнитного потока [Вб/с],
∆Ф ― изменение магнитного потока [Вб],
∆t ― время, за которое происходит это изменение [c].
Кроме того, ЭДС индукции равна производной магнитного потока по времени:
$varepsilon_i = -text{Ф}_t’$
где:
- ― ЭДС электромагнитной индукции [B],
- ― производная магнитного потока по времени [Вб/с].
Задача 1
Замкнутый контур площадью S из тонкой проволоки помещён в магнитное поле. Плоскость контура перпендикулярна вектору магнитной индукции поля. В контуре возникают колебания тока с амплитудой iм = 35 мА, если магнитная индукция поля меняется с течением времени в соответствии с формулой B = acos (bt), где a = 6 · 10-3Тл, b = 3500 c-1. Электрическое сопротивление контура R = 1,2 Ом. Чему равна площадь контура?
Решение:
Обратите внимание на величины, данные в условии. Они здесь совсем не такие, к которым вы привыкли, потому что не дано значение магнитного поля, а дана зависимость магнитного поля от времени. Посмотрим, как это скажется на решении задачи.
Поскольку магнитное поле, а вместе с ним и поток меняются, то будет возникать ЭДС индукции, именно это ЭДС и вызовет электрический ток, поэтому запишем закон электромагнитной индукции.
По закону электромагнитной индукции $varepsilon_i = -frac{Delta text{Ф}}{Delta t}$
ЭДС — это изменение магнитного потока за время. Ничего в определении ЭДС не сказано про это самое время. Дело в том, что изменение какой-то величины за небольшой промежуток времени называется производной по времени. То есть наше ЭДС, которое является изменением магнитного потока за небольшой промежуток времени, это просто производная магнитного потока по времени $varepsilon_i = -text{Ф}_t’$
И это очень важный момент, без которого мы не сможем решить такого рода задачу.
Теперь посчитаем ЭДС индукции.
Напишем, чему равен магнитный поток Ф = BS = acos (bt) · S.
ЭДС индукции — это производная магнитного потока по времени. Теперь придётся вспомнить немного математики. Множители “a” и “S” перед косинусом не зависят от времени, поэтому производная их не трогает, а вот у косинуса в скобках стоит зависимость от времени, поэтому именно от косинуса производную и нужно взять.
Обратите внимание на полученную формулу магнитного потока. В ней стоит просто множитель aS перед сложной функцией косинуса
$text{Ф} underset{text{множитель}}{underbrace{aS}} ;; cdot ;; underset{text{сложная функция}}{underbrace{cos(bt)}}$.
Взяв производную от этой функции, получаем Ф´ = –abS · sin (bt). А теперь, раз мы знаем производную магнитного потока, значит, знаем и ЭДС индукции, потому что $varepsilon_i = -text{Ф}_t’$
Подставив сюда значение производной, получим $varepsilon_i = -text{Ф}_t’$ = abS · sin (bt).
Мы получили значение ЭДС. Кроме этого, мы знаем сопротивление и максимальную силу тока, поэтому запишем закон Ома.
По закону Ома $I = frac{varepsilon}{R}$ , подставив сюда значение ЭДС, получаем $I = frac{abScdot sin(bt)}{R}$.
Мы получили зависимость силы тока от времени.
Из-за синуса, который стоит в этой формуле, ток постоянно меняет свое значение, то он становится больше, то меньше, поскольку синус меняет своё значение от -1 до 1.
В условии дано максимальное значение силы тока, которое протекает по контуру. Когда эта величина будет максимальной? В тот момент, когда синус будет максимальным, то есть равный единице. Поэтому запишем sin (bt) = 1.
Максимальное значение тока будет в тот момент, когда будет максимальным значение ЭДС индукции, то есть когда, $I_{max} = frac{abS}{R}$.
Отсюда можно легко выразить площадь контура $S = frac{I_{max}R}{ab}$, подставив сюда все значения, получим $S = frac{I_{max}R}{ab} = frac{35cdot 10^{-3} Acdot 1,2text{Ом}}{6cdot 10^{-3}text{Тл} cdot 35000c^{-1}} = 0,002text{м}^2$
Ответ: 0,002
Как видно из формулы магнитного потока Ф = BScosα, изменение магнитного потока может быть вызвано разными факторами:
- увеличением или уменьшением модуля индукции магнитного поля (т. е. величины $frac{Delta B}{Delta t}$);
- изменением направления вектора магнитного поля (т. е. изменением угла α);
- деформацией контура, причем такой деформацией, при которой изменяется площадь контура (т. е. изменением величины $frac{Delta S}{Delta t}$ );
- изменением нескольких из этих величин одновременно.
Таким образом, изменение модуля или направление вектора магнитной индукции или площади контура неизбежно приводят к тому, что в контуре возникает электродвижущая сила.
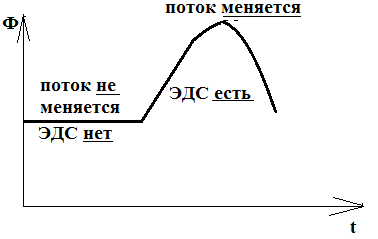
Если нарисовать график зависимости магнитного потока, то он может выглядеть либо так: тогда поток не будет менятьсяи ЭДС не возникает.
Либо так, тогда будет меняться поток и возникать ЭДС:
Знак «минус» перед скоростью изменения магнитного потока в формуле отражает правило Ленца: индуцированный ток всегда направлен так, чтобы магнитное поле, которое он создает, препятствовало изменению магнитного потока.
Если магнитный поток, проходящий через площадь контура, уменьшается, то магнитное поле индуцированных токов будет стремиться его увеличить.
Если поток увеличивается ― магнитное поле индуцированных токов будет стремиться его уменьшить.
Задача 2
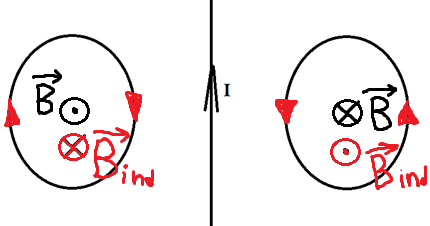
Два проводящих кольца расположены относительно проводника с током в одной плоскости, как это показано на рисунке. В каком направлении будет индуцироваться ток в этих кольцах, если начать двигать их в направлении проводника?
Решение:
Первым делом необходимо понять, как вообще может возникать индуцированный ток, если даже магнитного поля нет?
Его направление мы можем определить по правилу правого винта. Отметим это на рисунке.
Теперь эти два проводника начинают двигать. Разве от этого меняется поток? Ведь площадь остаётся та же самая, угол между нормалью и вектором тоже не меняется. Однако, чем ближе к проводнику с током, тем сильней поле, а чем дальше от него, тем слабее! Поэтому, когда мы двигаем кольца к проводнику, мы увеличиваем поток, ведь ближе поле сильнее. Значит, будет появляться ток, а его направление можно определить по правилу Ленца. Что нам говорит правило Ленца?
Раз поток увеличивается, то по правилу Ленца ток будет индуцироваться так, чтобы уменьшить поток, то есть магнитное поле в левом кольце будет направлено от нас, а в правом ─ на нас. А значит, по правилу правого винта мы можем определить, что ток будет течь по часовой стрелке слева и против часовой стрелки справа.
Движение проводников
Если к концам проводника, движущегося в магнитном поле, подключить вольтметр, то прибор покажет наличие разности потенциалов на концах проводника. Таким образом, когда проводник перемещается в области с магнитным полем, в нем возникает электромагнитная движущая сила (ЭДС).
Согласно закону Лоренца, в проводнике, движущемся в магнитном поле, создается ЭДС $|varepsilon_i| = Blvsinalpha$;
где:
$varepsilon_i$― ЭДС электромагнитной индукции [B],
B ― индукция магнитного поля [Тл],
l ― длина проводника [м],
v ― скорость движения проводника [м/с],
α ― угол между направлением вектора скорости $overrightarrow{v}$ и длиной проводника $overrightarrow{l}$ , если вектор индукции магнитного поля $overrightarrow{B}$перпендикулярен проводнику и вектору скорости его движения: $overrightarrow{B} perp overrightarrow{v}, overrightarrow{B} perp overrightarrow{l}$
Используя силу Лоренца, можно получить это определение ЭДС. Сила Лоренца ― это проявленное действие магнитного поля на заряженную частицу.
В проводнике присутствует большое количество свободных зарядов (именно это отличает проводники от диэлектриков), и на каждый из зарядов действует сила Лоренца, перемещая их по проводнику так, что в одной его части скапливается отрицательный заряд, а в другой, соответственно, положительный. Это распределение зарядов и является физической основой для возникновения электродвижущей силы.
На рисунке показано как сила Лоренца, действующая на каждый из зарядов проводника, создаёт ЭДС в проводнике. Если одиночный отрицательный заряд попадает в магнитное поле, направленное от нас, то, согласно правилу левой руки, направление его движения изменяется так, как показано на рисунке. Если в область с таким же магнитным полем входит проводник, суммарный заряд которого равен нулю, но внутри которого находятся электроны, способные свободно перемещаться в проводнике, то электроны стекаются в один конец проводника. Так как электроны переместились в один конец проводника, то этот конец приобретает отрицательный заряд, а противоположный ему ― положительный. Таким образом, в проводнике возникает разность потенциалов и электродвижущая сила.
В некоторых случаях удобно решать задачи, используя определение ЭДС через закон Лоренца (обычно это задачи о движении прямолинейного проводника в поле), в других ― через закон Фарадея.
В проводнике, движущемся в магнитном поле, образуется разность потенциалов U = lvBsinα;
где:
U — разность потенциалов [В],
l — длина проводника [м],
v — скорость движения проводника $big[ frac{text{м}}{c} big]$
B — индукция магнитного поля [Тл],
α — угол между направлением скорости и длиной проводника.
В случае, если есть какой-то замкнутый контур, то ЭДС в нем возникает только тогда, когда меняется магнитный потокчерез этот контур. В случае же тонкого стержня, для которого нельзя применить понятия магнитного потока, потому что у него просто нет площади, ЭДС возникает при движении в постоянном магнитном поле.
В случае, если в задаче дана проводящая рамка или контур, для определения ЭДС (напряжения) используем формулу $varepsilon_i = — frac{Delta text{Ф}}{Delta t}$
В случае, если в задачи дан проводник, движущейся в поле, для определения ЭДС (напряжения) используем формулу $varepsilon$ =U= lvBsinα.
Задача 3
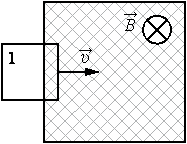
В заштрихованной области на рисунке действует однородное магнитное поле, перпендикулярное плоскости рисунка с индукцией В = 0,1 Тл. Квадратную проволочную рамку, сопротивление которой 10 Ом и длина стороны 10 см, перемещают в этом поле в плоскости рисунка поступательно равномерно с некоторой скоростью υ. При попадании рамки в магнитное поле в положении 1 в ней возникает индукционный ток, равный 1 мА. Какова скорость движения рамки?
Решение:
Составим цепочку.
Зная силу тока и сопротивление, что можно найти? Мы сможем найти напряжение, то есть ЭДС, а ЭДС, уже можно легко связать со скоростью движения рамки.
Составим цепочку. Мы знаем магнитное поле (В), длину стороны (a), сопротивление (R) и силу тока (I), а найти нужно скорость(v).
Зная ток и сопротивление, что сразу можно найти? Напряжение, то есть ЭДС, которое мы сможем найти по закону Ома.
А связать ЭДС с индукцией поля, стороной рамки и скоростью движения очень легко, воспользовавшись той формулой, которую мы получили в прошлой задаче.
Пройдёмся вдоль этой цепочки.
Запишем закон Ома $I = frac{varepsilon}{R}$, подставив сюда формулу для ЭДС, которую мы получили в прошлой задаче, отбросив знак «минус» получим $I = frac{varepsilon}{R} = frac{Bav}{R}$отсюда выразим скорость, и, подставив все величины, получим $v = frac{IR}{Ba} = frac{1cdot 10^{-3} Acdot 10text{Ом}}{0,1 text{Тл} cdot 0,1 text{м}} = 1 frac{text{м}}{c}$
Ответ: 1