Расчет электрической цепи
Задача 1
От источника постоянного тока получает питание
цепь, состоящая их ряда сопротивлений, включенных смешанно, величины которых
известны. Э.Д.С. источника — Е, внутреннее сопротивление — R0.
Начертить схему цепи и определить:
1. эквивалентное сопротивление цепи.
2. токи и напряжения на каждом
сопротивлении схемы.
. расход энергии цепью за время t
= 10ч.
Решение проверить составлением баланса
мощностей.
|
Е, |
100 |
|
R0, Ом |
0,2 |
|
R1, |
10 |
|
R2, |
1 |
|
R3, |
9 |
|
R4, |
3 |
|
R5, |
20 |
|
R6, |
5 |
|
R7, |
12 |
|
R8, |
4 |
|
R9, |
3 |
|
R10,Ом |
6 |
Решение:
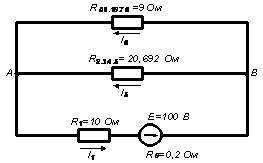
1. Начертим
схему цепи, обозначим токи и узлы.
2. Определим
эквивалентное сопротивление цепи Rэкв:
Цепь имеет смешанное соединение.
3. Начнем
с участка АСВ:
участок АСВ состоит из двух участков: АС и СВ
соединенных последовательно;
на участке АС сопротивления R2,
R3
и R3
включены параллельно, сопротивление R234:
;
Ом;
участок АСВ имеет последовательное соединение,
сопротивление на участке АСВ:
Ом;
4. Участок
AEDB:
участок ED
имеет параллельное соединение резисторов и
;
Ом;
участок АED
имеет последовательное соединение, сопротивление на участке АED:
Ом;
участок AD
имеет параллельное соединение резисторов и
;
Ом;
участок АEDB
имеет последовательное соединение, сопротивление на участке АEDB:
Ом;
Схема приобретает вид:
5. Участок
AB:
участок АВ имеет параллельное соединение:
Ом;
Схема приобретает вид:
6. Общее
сопротивление цепи :
Ом;
Схема приобретает вид:
7. По
закону Ома для замкнутой цепи определим ток I1:
А;
8. По
закону Ома для участка цепи определим напряжение на резисторе R1:
В;
9. Определим
напряжение приложенное к цепи:
сумма падений напряжения на внутреннем
сопротивлении источника тока и на внешней цепи равна ЭДС источника:
;
отсюда:
В;
10. По
закону Ома для участка цепи определим напряжение на резисторе :
В;
11. Определим
токи и
:
А;
А;
12. По
первому закону Кирхгофа сделаем проверку в узле А:
А;
Токи определили верно.
13. По
закону Ома для участка цепи определим напряжение на резисторе :
В;
14. По
закону Ома для участка цепи определим напряжение на резисторе :
В;
так как резисторы включены
параллельно, то напряжения приложенные к каждому из них будут одинаковыми:
В;
15. Определим
токи ,
:
А;
А;
А;
16. По
закону Ома для участка цепи определим напряжение на резисторе :
В;
17. По
закону Ома для участка цепи определим напряжение на резисторе :
В;
18. По
закону Ома для участка цепи определим ток на резисторе :
А;
19. По
первому закону Кирхгофа определим ток I8
из
узла А:
А;
20. По
закону Ома для участка цепи определим напряжение на резисторе :
В;
21. По
закону Ома для участка цепи определим напряжение на резисторе :
В;
22. По
закону Ома для участка цепи определим ток на резисторе :
А;
23. По
закону Ома для участка цепи определим ток на резисторе :
А;
24. Определим
расход энергии цепью за время t
= 10ч:
Рассчитаем мощность, потребляемую всей цепью:
Вт;
Расход энергии за 10 часов работы равен:
Вт∙час;
25. Для
проверки решения составим уравнение баланса мощностей:
;
Вт;
1,621 Вт;
Вт;
Вт;
Вт;
Вт;
Вт;
Вт;
Вт;
Вт;
;
,631≈ 599,601;
Неточность допущена при округлениях в расчетах.
Задача решена верно.
Задача 2
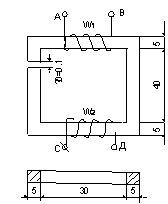
Магнитная цепь, схема которой приведена на
рис.2, состоит из двух вертикальных стержней и двух горизонтальных ярем.
Размеры цепи заданы в сантиметрах. В магнитной цепи предусмотрен зазор 0,1 см.
На ярмах расположены обмотки с числом витков W1и
W2.
Зажимы обмоток А, В, С и Д соединены так, как указано в таблице вариантов, при
этом получается согласное или встречное соединение обмоток, что следует
студенту определить самостоятельно.
Найти:
) необходимую силу тока для получения в
сердечнике заданного магнитного потока Ф (или магнитной индукции В);
) абсолютную магнитную проницаемость и магнитную
проницаемость на участке, где расположены обмотки;
)потокосцепление и индуктивность обмоток;
Начертить схему магнитной цепи для своего
варианта.
Магнитный поток, В —
Магнитная индукция,
Тл 0,8
W1 200
W2 900
Обозначения величин
Материал стержней Чугун
Материал ярем Э11
Какие зажимы
обмоток соединены вместе — В, С
|
Индукция, |
Напряженность |
||||
|
Т |
Гс |
Электротехническая |
Литая |
Чугун |
|
|
Э |
Э |
||||
|
0,25 |
2 |
100 |
25 |
200 |
1 |
|
0,3 |
3 |
113 |
29 |
240 |
1 |
|
0,35 |
3 |
126 |
33 |
280 |
1 |
|
0,4 |
4 |
140 |
37 |
320 |
1 |
|
0,45 |
4 |
155 |
42 |
360 |
1 |
|
0,5 |
5 |
171 |
48 |
400 |
2 |
|
0,55 |
5 |
190 |
55 |
443 |
2 |
|
0,6 |
6 |
211 |
63 |
488 |
2 |
|
0,65 |
6 |
236 |
73 |
535 |
3 |
|
0,7 |
7 |
261 |
84 |
584 |
3 |
|
0,75 |
7 |
287 |
96 |
632 |
4 |
|
0,8 |
8 |
318 |
110 |
682 |
5 |
|
0,85 |
8 |
352 |
125 |
745 |
6 |
|
0,9 |
9 |
397 |
140 |
798 |
7 |
|
0,95 |
9 |
447 |
160 |
860 |
8 |
|
1,0 |
10 |
502 |
185 |
924 |
10 |
|
1,1 |
11 |
647 |
260 |
1 |
14 |
|
1,2 |
12 |
843 |
380 |
1 |
19 |
|
1,3 |
13 |
1 |
680 |
1 |
26 |
|
1,4 |
14 |
1 |
1 |
2 |
34 |
|
1,5 |
15 |
2 |
3 |
2 |
47 |
|
1,6 |
16 |
4 |
5 |
4 |
— |
|
1,7 |
17 |
7 |
9 |
— |
— |
|
1,8 |
18 |
12 |
14 |
— |
— |
Дано:
Магнитная индукция — В = 0,8 Тл
W1 = 200
W2
= 900
материал стержней: чугун
материал ярем: Э11
соединены вместе зажимы В, С
Решение:
1. Размеры магнитопровода по средней
магнитной линии:
Т.к. площадь сечения во всей магнитной цепи
одинаково, то в качестве длины цепи принимаем длину средней магнитной линии
потока. (Среднеарифметическое между наружным и внутренним периметром магнитной
цепи минус воздушный зазор) l = 159,9 см;
длина воздушного зазора l0 = 0,1 см;
Толщина сердечника 50 мм.
S = 5 ∙ 5 = 25
см2 = 25 ∙ 10-4 м2;
S0
= 5 ∙ 5 = 25 см2 = 25 ∙ 10-4 м2;
2. Соединение обмоток — согласованное.
. Магнитный поток в данном магнитопроводе:
Ф = В · S = 0,8 · 25 · 10-4
= 20 · 10-4 Вб.
4. Магнитная индукция и воздушном зазоре В0
= В = 0,8 Тл, т.к. S=S0.
. Напряженность магнитного поля для участка из
чугуна находим по табл.2.1: при В = 0,8 Т Нч = 54 А/см;
. Напряженность магнитного поля для участка из
электротехнической стали Э11 находим по табл.2.1: при В = 0,8 Т Н = 3,18 А/см;
. Напряженность магнитного поля в воздушном
зазоре находим по формуле:
Н0 = 0,8 ∙ В ∙ 104
= 0,8 ∙ 0,8 ∙ 104 = 6400 М/см
8. По закону полного тока находим
ток в обмотках:
А;
. Определим магнитную проницаемость по
формуле
= μ∙Н
μ = В/Н = 0,8/54 =
0,0148 ;
. Абсолютная магнитная проницаемость:
μа
= В/µ0 Н = 0,8/1,256·10-6 ·54 = 0,0118 ·106 ;
. Относительная магнитная проницаемость:
μr
= µ/µ0 = 0,0148 /0,0118 ·106 = 1,254·10-6 ;
12. Определим потокосцепление и индуктивность
обмоток:
Ψ1
= W∙Ф = 200 ∙ 20 ·
10-4 = 0,4;
Ψ1
= W∙Ф = 900 ∙ 20 ·
10-4 = 1,8;
. Определим индуктивность обмоток:
L=Ф/I;
L = 20 · 10-4/3,816
= 5,241· 10-4 Гн;
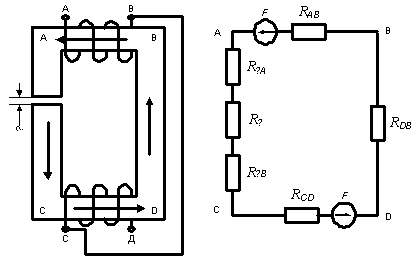
Схема магнитной цепи:
Задача 3
К зажимам цепи однофазного переменного тока
приложено напряжение U
(рис. схема а, б). Величины сопротивлений цепи R1,
R2,
XL1,
XL2,
XC1,
XC2 приведены
в таблице вариантов. Начертить схему для своего варианта и определить:
) токи в цепи;
) коэффициент мощности (cosφ)
цепи;
) активную Р, реактивную Q,
полную S мощности цепи,
потребляемые цепью;
) построить в масштабе векторную диаграмму.
Обозначения величин U,
В 36
Схема цепи а
Обозначения величин
R1,
Ом —
R2,
Ом 5
XL1,
Ом 2
XL2,
Ом —
XC1,
Ом 4
Схема цепи а).
Решение:
. Начертим схему цепи:
2. Определим полное сопротивление цепи Z:
;
XС
= XС1
+ XС2
= 4 + 3 = 7 Ом — арифметическая сумма однотипных индуктивного и емкостного
сопротивлений;
Ом;
2. По закону Ома для цепи переменного тока
определим ток цепи I:
= U / Z = 36/7,07= 5,09А;
3. Из треугольника сопротивлений определим
угол φ:
; угол составит 45º;
4. Полная мощность цепи:
S = U
∙
I = 36 ∙ 5,09
= 183,24 ВА;
5. По формуле P
= S ·
Cos φ определим
активную мощность цепи:
Р = 183,24 · 0,707 = 129,55 Вт;
6. Из формулы треугольника мощностей
определим реактивную мощность Q:
Вар;
7. Построение векторной диаграммы:
8. При построении векторной диаграммы
исходим из следующих условий: Ток одинаков для любого участка цепи, так как
разветлений нет; На каждом сопротивлении при
прохождении тока создается падение напряжения, значение которого определяем по
закону Ома для участка цепи;
9. Задаемся масштабом: mu= 4 в/см; mI=
1А/см;
Для построения векторов напряжений определим
напряжения на активном и индуктивном сопротивлениях:
UR2 = I ·R2 = 5,09
· 5 = 25,45 В;XL1 = I ·XL1 = 5,09 · 2 = 10,18 В;XС1 =
I ·XС1 = 5,09 · 4 = 20,36 В;XC2 =
I ·XL2 = 5,09 · 3 = 15,27 В
Определим длины векторов:
UR2 =
UR2/mu = 25,45 /4 = 6,36 см;UL1 = UXL1/mu
= 10,18 /4 = 2,54 см;UС1 = UXC1/mu = 20,36 /4
= 5,09 см;UC2 = UXC2/mu = 15,27 /4 = 3,82 см;I
= I/mI = 5,09 /1 = 5,09 см;
По горизонтали откладываем вектор тока Ī,
вдоль
вектора тока Ī откладываем вектор
напряжения на активном сопротивлении ŪR2
(при активном сопротивлении ток совподает с напряжением). От конца вектора ŪR2
откладываем вектор напряжения ŪL1
на индуктивном сопротивлении в сторону опережения от вектора тока Ī
на
90º
(при
индуктивном сопротивлении направление тока опережает от направления напряжения
на 90º).
От
конца вектора ŪL1 откладываем
вектор ŪL2.
От конца вектора ŪL2
откладываем вектор напряжения ŪC1
на емкостном сопротивлении в сторону отставания от вектора тока Ī
на
90º
(при
емкостном сопротивлении направление тока отстает от направления напряжения на
90º).
Геометрическая
сумма векторов ŪR2,
ŪL1, ŪL2
и ŪC1
равна напряжению Ū, приложенному
к цепи. Косинус угла φ между
вектором Ū и Ī
является
коэффициентом мощности цепи.
Задача 4
электрический магнитный цепь
выпрямитель
В четырехпроводную трехфазную линию с линейным
напряжением Uл
включается треугольником или звездой (согласно варианту) потребитель, в фазах
которого соединяются последовательно активные, индуктивные и емкостные
сопротивления в соответствии с таблицей вариантов. Начертить схему включения
потребителя для своего варианта и определить:
) фазные и линейные токи;
) углы сдвига фаз в каждой фазе;
) построить в масштабе векторную диаграмму и с
ее помощью определить величину тока в нулевом проводе («звезда»), либо линейные
токи («треугольник»);
) определить активную, реактивную и полную
мощности всей цепи.
Uл
= 127 В;
соединение треугольник;
фаза АВ
R = 6 Ом;
XС
= 8 Ом;
фаза СА
R = 7 Ом;
XС
= 6 Ом;
фаза ВС
XС
= 15 Ом;
Решение:
. При соединении треугольником фазное напряжение
равно линейному, т. е. Uф
=
Uл =
127 В;
. Определим полное сопротивление в фазе
СА:
;
Ом;
3. Определим ток в фазе СА:
ICA = U/
Z = 127/9,22
= 13,77 A;
. Определим полное сопротивление в фазе
АВ:
;
Ом;
5. Определим ток в фазе АВ:
IAB = U/
Z = 127/10
= 12,7 A;
. Определим полное сопротивление в фазе
ВС:
;
Ом;
7. Определим ток в фазе ВС:
IBC
= U/ Z
= 127/15 = 8,47 A;
. Определим углы сдвига фаз в каждой
фазе:
в фазе СА:
: угол 40,6º;
в фазе АВ:
; угол 66,4º;
в фазе ВС:
; угол 90º;
9. определим активную, реактивную и полную
мощности всей цепи:
в фазе СА:
ВА;
P = S ·
Cos φ;
P = ·
0,759 = 1327,33 Вт:
Вар;
в фазе АВ:
ВА;=
S ·
Cos φ;
P = ·
0,4 = 645,16 Вт:
Вар;
в фазе ВС:
ВА;=
S ·
Cos φ;
P = ·
0 = 0 Вт:
Вар;
Полная мощность всей цепи S:
S = ВА;
Активная мощность всей цепи Р:
Р = 1327,33 + 645,16 + 0 = 1972,49 Вт;
Реактивная мощность всей цепи Q:
Q = +
+
=
3692,55
Вар;
. Построение векторной диаграммы:
Задаемся масштабом: по току МI=2
А/см; по напряжению МU=20
В/см.
Длина векторов фазных (линейных) напряжений:
LUф=
Длина векторов фазных токов:
LСА=
LАВ=
LBС=
При построении векторной диаграммы вначале
откладываем три вектора фазных (линейных) напряжений с углом сдвига фаз
относительно друг друга 120°. Векторы фазных токов отстают от вектора фазных
напряжений, т. к. нагрузка емкостная. В фазе АВ на угол φ=66,4°,
в фазе СА на угол φ=40,6°, в
фазе ВС на угол φ=90°.
Векторы
линейных токов являются геометрической разностью векторов соответствующих
фазных токов:
=
—
;
=
—
;
=
—
;
. По векторной диаграмме определим
линейные токи:
IA
= 23,8 А;
IB
= 20 А;
Задача 5
Мостовой выпрямитель должен питать потребитель
постоянным током. Мощность потребителя Р0, Вт, при напряжении
питания U0,
В. Следует выбрать один из трех типов полупроводниковых диодов, параметры
которых приведены в табл. 5.11 для схемы выпрямителя, и пояснить, на основании
чего сделан выбор. Начертить схему выпрямителя.
Р0 = 300 Вт; U0 = 40 В;
диоды:
Д214; Iдоп
= 5 А; Uобр
= 100 В;
Д215Б; Iдоп
= 2 А; Uобр
= 200 В;
Д224А; Iдоп
= 10 А; Uобр
= 50 В;
Решение:
1. Схема мостового выпрямителя:
2. Найдем напряжение Uв,
действующее на диод в непроводящий период для мостовой схемы выпрямителя:
;
В;
. Определим ток потребителя Iп
из формулы мощности:
;
А;
. По значениям I0
=
7,5 А и Uв
= 62,8 В выбираем из табл. 5.1
4. Из предложенных диодов выбираем диод
Д214, который удовлетворяет условию:
;
;
Условию, ;
,
не удовлетворяет. Для того, чтобы выполнить условие необходимо
в цепь включить параллельно 2 диода Д214. В этом случае Iобр=Iв
+
Iв =
5 + 5 = 10 A, что удовлетворяет
условию ,
;
5. Составим схему выпрямителя с двумя
параллельно включенными диодами Д214:
Задача 6
Для транзистора, включенного по
схеме с общим эмиттером, используя входную и выходную характеристики,
определить коэффициент усиления h21э, величину сопротивления
нагрузки Rk1 и Rk2и мощность
на коллекторе Рk1и Рk2, если
известно напряжение на базе Uбэ, напряжение
на коллекторе Ukэ1 и Ukэ2 и напряжение
источника питания Еk. Данные для
своего варианта взять из табл. 6.1
|
Номера |
Uбэ, В |
Ukэ1, В |
Ukэ2, В |
Еk, |
|
3, |
0,3 |
20 |
30 |
40 |
1 Схема:
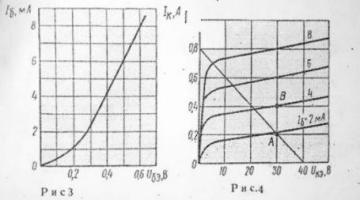
1. Определяем коэффициент усиления h21э
по выходным характеристикам:
21э=ΔIк/
ΔIб=(0,4-0,21)/(0,004-0,002)=95
2. Определяем ток в цепях базы и коллектора
по входным характеристикам: Iб= 4 мА, следовательно для заданных
параметров
Iк=
h21э· Iб =95·0,004=0,38А.
3. Определяем сопротивления Rk1
и Rk2:
для Rк1
:
Ом;
для Rк2
:
Ом;
4. Определяем ток на коллекторе Ik1:
А;
5. Определяем ток на коллекторе Ik2:
А;
6. Pк1=
Uкэ1·
Iк1 =
20·0,38 = 7,6 Вт;
7. Pк2=
Uкэ2·
Iк2 =
30·0,126 = 3,78 Вт;
Найди верный ответ на вопрос ✅ «В цепи постоянного тока U=220, I=5A. Определить мощность потребителя и расход электроэнергии за 8 часов работы …» по предмету 📙 Физика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Главная » ⭐️ Физика » В цепи постоянного тока U=220, I=5A. Определить мощность потребителя и расход электроэнергии за 8 часов работы
Ну, начнём. R5 и R6 соединены последовательно, значит напряжения между ними распределены пропорционально их сопротивлениям, то есть U5/R5 = U6/R6
5В/10 Ом = U6/2 Ом, U6 = 5В/10 Ом × 2 Ом = 1 В
Суммарное напряжение на этих двух резисторах U56 = U5+U6 = 5В + 1В = 6В.
Резисторы R2, R3, R4 подсоединены парралельно к ветке R5R6, значит напряжения на них будут одинаковы: U2=U3=U4=U56 = 6В
Найдем силу тока в каждой ветке:
I2 = U2/R2 = 6В / 2 Ом = 3А
I3 = U3/R3 = 6В / 6 Ом = 1А
I4 = U4/R4 = 6В / 4 Ом = 1,5А
I5 = I6 = I56 = 6В / (5 Ом + 1 Ом) = 1А
В сумме эти токи дадут общий ток в цепи:
I = I2+I3+I4+I56 = 3А+1А+1,5А+1А = 6,5А
Ток I1 по законам последовательного соединения будет равен току I = 6,5A.
Напряжение на резисторе R1 будет равно
U1 = R1×I1 = 4 Ом × 6,5А = 26В.
Общее напряжение в цепи будет равно
U = U1 + U56 = 26В + 6В = 32В
Мощность цепи найдем так:
P = U×I = 32В × 6,5А = 208 Вт
208 Вт = 0,208 кВт
За 8 часов потребление электроэнергии составит 0,208 кВт × 8 часов = 1,664 кВт×ч.
Исключаем резистор R3. Что изменится?
Изменится общее сопротивление участка с параллельно соединенными резисторами.
Обозначим его как Rпр
1/Rпр = 1/R2 + 1/R4 + 1/(R5+R6) = 1/2 + 1/4 + 1/12 = 10/12 Ом^-1
Перевернем дробь и получим Rпр = 12/10 = 1,2 Ом.
Тогда Rобщ = R1 + Rпр = 4 Ом + 1,2 Ом = 5,2 Ом
I = U/Rобщ = 32 В / 5,2 Ом ≈ 6,15А
Напряжение на Rпр будет равно
Uпр = I×Rпр = 6,15 А × 1,2 Ом ≈ 7,38 В
Напряжение U4 будет равно этому же напряжению, то есть оно увеличится на 1,38 В после изъятия из схемы резистора R3.
Пипец…
Большинство бытовых приборов, подключаемых к сети, характеризуются таким параметром, как электрическая мощность устройства. С физической точки зрения мощность представляет собой количественное выражение совершаемой работы. Поэтому для оценки эффективности того или иного устройства вам необходимо знать нагрузку, которую он будет создавать в цепи. Далее мы рассмотрим особенности самого понятия и как найти мощность тока, обладая различными характеристиками самого устройства и электрической сети.
Понятие электрической мощности и способы ее расчета
С электротехнической точки зрения она представляет собой количественное выражение взаимодействия энергии с материалом проводников и элементами при протекании тока в электрической цепи. Из-за наличия электрического сопротивления во всех деталях, задействованных в проведения электротока, направленное движение заряженных частиц встречает препятствие на пути следования. Это и обуславливает столкновение носителей заряда, электроэнергия переходит в другие виды и выделяется в виде излучения, тепла или механической энергии в окружающее пространство. Преобразование одного вида в другой и есть потребляемая мощность прибора или участка электрической цепи.
В зависимости от параметров источника тока и напряжения мощность также имеет отличительные характеристики. В электротехнике обозначается S, P и Q, единица измерения согласно международной системы СИ – ватты. Вычислить мощность можно через различные параметры приборов и электрических приборов. Рассмотрим каждый из них более детально.
Через напряжение и ток
Наиболее актуальный способ, чтобы рассчитать мощность в цепях постоянного тока – это использование данных о силе тока и приложенного напряжения. Для этого вам необходимо использовать формулу расчета: P = U*I
Где:
- P – активная мощность;
- U – напряжение приложенное к участку цепи;
- I — сила тока, протекающего через соответствующий участок.
Этот вариант подходит только для активной нагрузки, где постоянный ток не обеспечивает взаимодействия с реактивной составляющей цепи. Чтобы найти мощность вам нужно выполнить произведение силы тока на напряжение. Обе величины должны находиться в одних единицах измерения – Вольты и Амперы, тогда результат также получится в Ваттах. Можно использовать и другие способы кВ, кА, мВ, мА, мкВ, мкА и т.д., но и параметр мощности пропорционально изменит свой десятичный показатель.
Через напряжение и сопротивление
Для большинства электрических устройств известен такой параметр, как внутреннее сопротивление, которое принимается за константу на весь период их эксплуатации. Так как бытовые или промышленные единицы подключаются к источнику с известным номиналом напряжения, определять мощность достаточно просто. Активная мощность находится из предыдущего соотношения и закона Ома для участка цепи, согласно которого ток на участке прямо пропорционален величине приложенного напряжения и имеет обратную пропорциональность к сопротивлению:
I = U/R
Если выражение для вычисления токовой нагрузки подставить в предыдущую формулу, то получится такое выражение для определения мощности:
P = U*(U/R)=U2/R
Где,
- P – величина нагрузки;
- U – приложенная разность потенциалов;
- R – сопротивление нагрузки.
Через ток и сопротивление
Бывает ситуация, когда разность потенциалов, приложенная к электрическому прибору, неизвестна или требует трудоемких вычислений, что не всегда удобно. Особенно актуален данный вопрос, если несколько устройств подключены последовательно и вам неизвестно, каким образом потребляемая электроэнергия распределяется между ними. Подход в определении здесь ничем не отличается от предыдущего способа, за основу берется базовое утверждение, что электрическая нагрузка рассчитывается как P = U×I, с той разницей, что напряжение нам не известно.
Поэтому ее мы также выведем из закона Ома, согласно которого нам известно, что падение напряжения на каком-либо отрезке линии или электроустановки прямо пропорционально току, протекающему по этому участку и сопротивлению отрезка цепи:
U=I*R
после того как выражение подставить в формулу мощности, получим:
P = (I*R)*I =I2*R
Как видите, мощность будет равна квадрату силы тока умноженной на сопротивление.
Полная мощность в цепи переменного тока
Сети переменного тока кардинально отличаются от постоянного тем, что изменение электрических величин, приводит к появлению не только активной, но и реактивной составляющей. В итоге суммарная мощность будет также состоять активной и реактивной энергии:

Где,
- S – полная мощность
- P – активная составляющая – возникает при взаимодействии электротока с активным сопротивлением;
- Q – реактивная составляющая – возникает при взаимодействии электротока с реактивным сопротивлением.
Также составляющие вычисляются через тригонометрические функции, так:
P = U*I*cosφ
Q = U*I*sinφ
что активно используется в расчете электрических машин.
Пример расчета полной мощности для электродвигателя
Отдельный интерес представляет собой нагрузка, подключенная к трехфазной сети, так как электрические величины, протекающие в ней, напрямую зависят от номинальной нагрузки каждой из фаз. Но для наглядности примера мы не будем рассматривать, как найти мощность несимметричного прибора, так как это довольно сложная задача, а приведем пример расчета трехфазного двигателя.
Особенность питания и асинхронной и синхронной электрической машины заключается в том, что на обмотки может подаваться и фазное и линейное напряжение. Тот или иной вариант, как правило, обуславливается способом соединения обмоток электродвигателя. Тогда мощность будет вычисляться по формуле:
S = 3*Uф*Iф
В случае выполнения расчетов с линейным напряжением, чтобы найти мощность формула примет вид:
Активная и реактивная мощности будут вычисляться по аналогии с сетями переменного тока, как было рассмотрено ранее.
Теперь рассмотрим вычисления на примере конкретной электрической машины асинхронного типа. Следует отметить, что официальная производительность, указываемая в паспортных данных электродвигателя – это полезная мощность, которую двигатель может выдать при совершении оборотов вала. Однако полезная кардинально отличается от полной, которую можно вычислить за счет коэффициента мощности.
Как видите, для вычислений с шильда мы возьмем следующую информацию об электродвигателе:
- полезная производительность – 3 кВт, а в переводе на систему измерения – 3000 Вт;
- коэффициент полезного действия – 80%, а в пересчете для вычислений будем пользоваться показателем 0,8;
- тригонометрическая функция соотношения активных и реактивных составляющих – 0,74%;
- напряжение, при соединении обмоток треугольником составит 220 В;
- сила тока при том же способе соединения – 13,3 А.
С таким перечнем характеристик можно воспользоваться несколькими способами:
S = 1,732*220*13,3 = 5067 Вт
Чтобы найти искомую величину, сначала определяем активную составляющую:
P = Pполезная / КПД = 3000/0.8 = 3750 Вт
Далее полную по способу деления активной на коэффициент cos φ:
S = P/cos φ = 3750/0.74 = 5067 Вт
Как видите, и в первом, и во втором случае искомая величина получилась одинакового значения.
Примеры задач
Для примера рассмотрим вычисление на участках электрической цепи с последовательным и параллельным соединением элементов. Первый вариант предусматривает ситуацию, когда все детали соединяются друг за другом от одного полюса источника питания до другого.
Как видите на рисунке, в качестве источника мы используем батарейку с номинальным напряжением 9 В и три резистора по 10, 20 и 30 Ом соответственно. Так как номинальный ток нам не известен, расчет произведем через напряжение и сопротивление:
P = U2/R = 81 / (10+20+30) = 1.35 Вт
Для параллельной схемы подключения возьмем в качестве примера участок цепи с двумя резисторами и одним источником тока:
Как видите, для удобства расчетов нам нужно привести параллельно подключенные резисторы к схеме замещения, из чего получится:
Rобщ = (R1*R2) / (R1+R2) = (10*15) / (10+15) = 6 Ом
Тогда искомый номинал нагрузки мы можем узнать через значение тока и сопротивления:
P = I2*R = 25*6 = 150 Вт