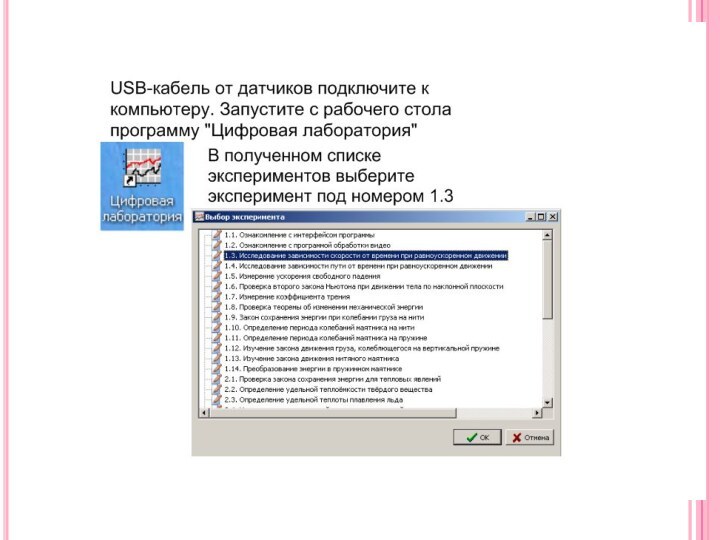
Лабораторная работа: «Исследование зависимости скорости от времени при равноускоренном движении»
ЛАБОРАТОРНАЯ РАБОТА №1
1.3 ЭЛЕКТРОННЫЙ ОТЧЕТ , СТР. 20
ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ СКОРОСТИ ОТ ВРЕМЕНИ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ
ЦЕЛИ РАБОТЫ:
1) Научиться пользоваться лабораторным комплексом «Цифровая лаборатория»
2) Исследовать движение бруска по наклонной плоскости
ОБОРУДОВАНИЕ:
1) Штатив с муфтой
2) Линейка магнитная
3) Герконовые датчики
4) Ноутбук с программным обеспечением
5) Деревянный блок
ЗАКРЕПИТЕ ЛИНЕЙКУ НА ШТАТИВЕ
Штатив поднимите на высоту не менее 30 см
Под нижний край линейки положите поролоновый коврик
ОБРАТИТЕ ВНИМАНИЕ!
Вначале надо подключить датчик, а потом открыть программу
Установите на линейку герконовые датчики: первые два — вплотную на отметке 15 см, вторые два — вплотную на отметке 25 см.
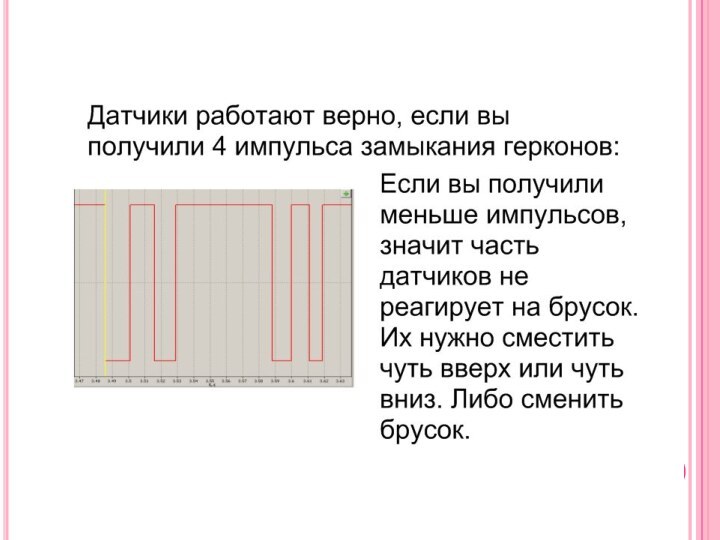
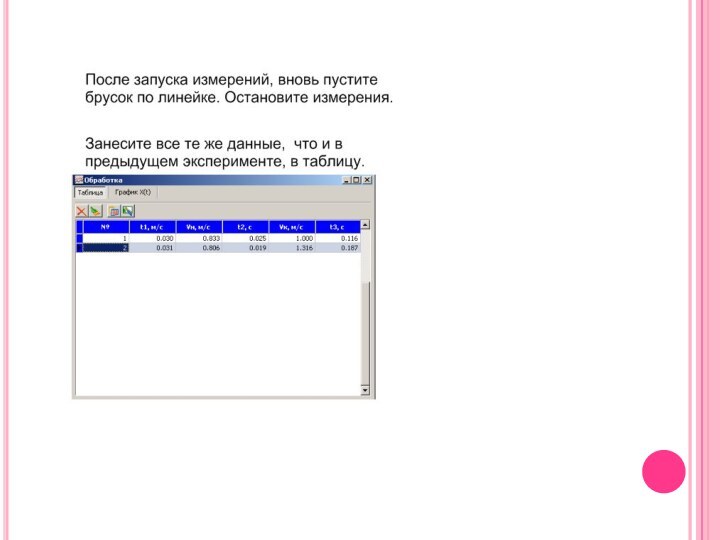
Получив 4 импульса, вы уже можете использовать их в качестве первых измерений:
Получив 4 импульса, вы уже можете использовать их в качестве первых измерений:
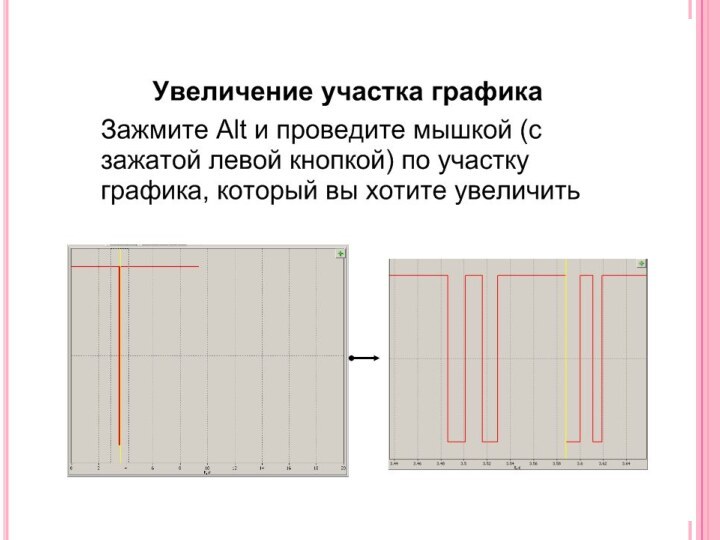
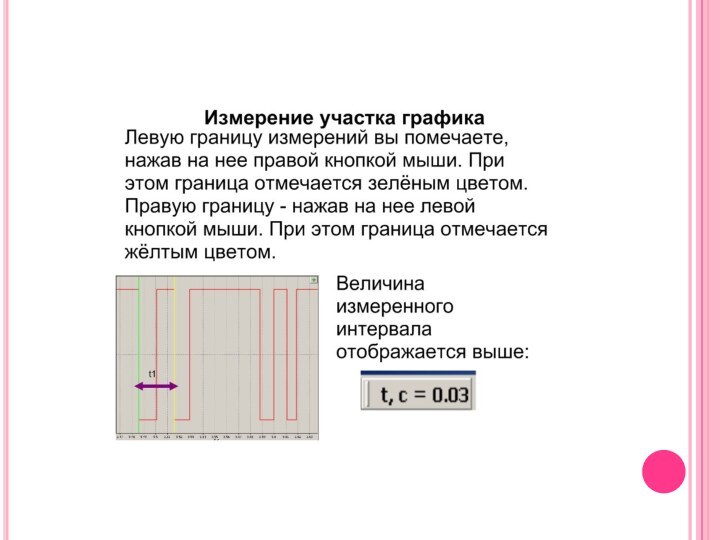
1) Увеличьте область графика, содержащую
4 импульса.
2) Измерьте участок графика, соединяющий начало 1 и начало 2 импульса.
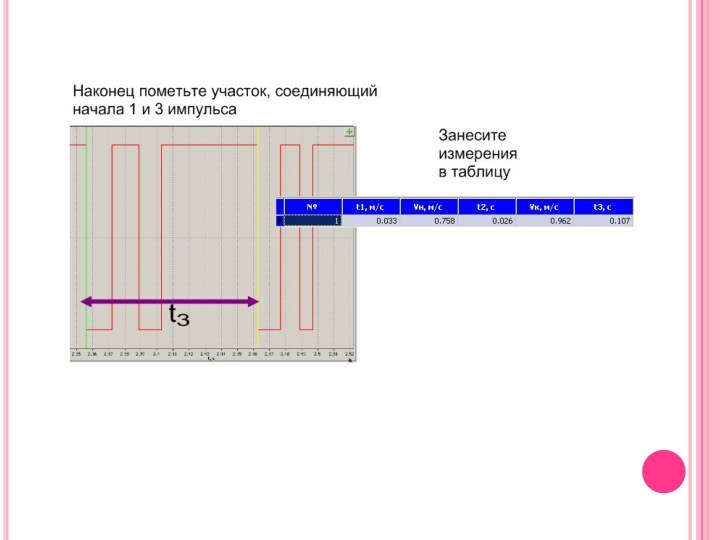
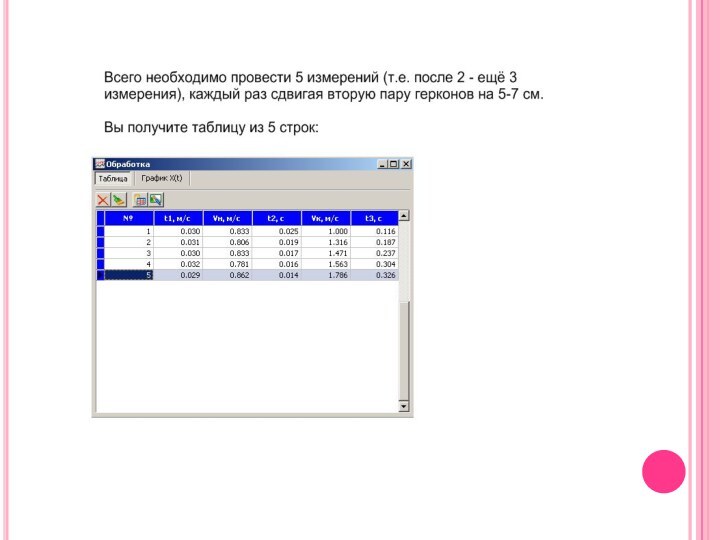
ПОЛУЧИВ ВСЕ ДАННЫЕ, СМЕСТИТЕ ВТОРУЮ ПАРУ ГЕРКОНОВ НА 7 СМ В СТОРОНУ ОТ ПЕРВОЙ ПАРЫ ГЕРКОНОВ (НА ОТМЕТКУ 32 СМ)
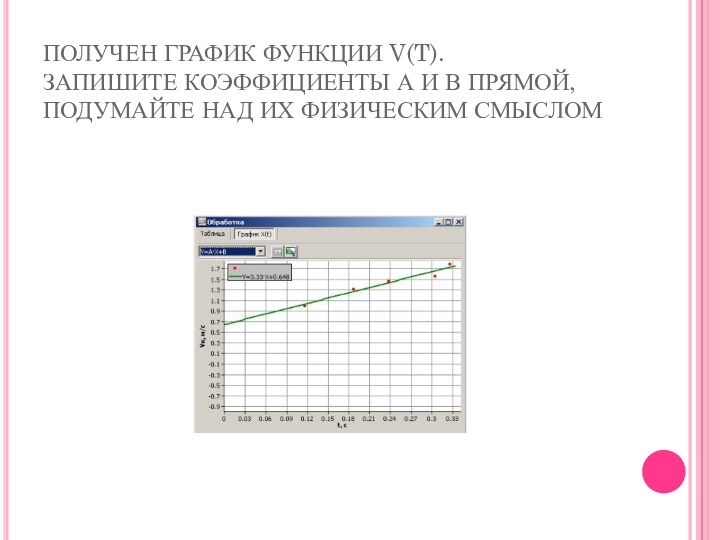
ПОЛУЧЕН ГРАФИК ФУНКЦИИ V(T).
ЗАПИШИТЕ КОЭФФИЦИЕНТЫ А И В ПРЯМОЙ, ПОДУМАЙТЕ НАД ИХ ФИЗИЧЕСКИМ СМЫСЛОМ
СОСТАВЛЕНИЕ ОТЧЕТА
СОСТАВЛЕНИЕ ОТЧЕТА
СОСТАВЛЕНИЕ ОТЧЕТА
ВЫВОДЫ
В выводе ответьте на следующие вопросы:
1) Как двигался брусок во время эксперимента?
2) Чему были равны начальная скорость (скорость при прохождении первой пары герконов) и ускорение бруска (из графика)?
3) Для чего 1 и 2, а также 3 и 4 герконы были установлены вплотную друг к другу?
СОХРАНЕНИЕ ОТЧЕТА
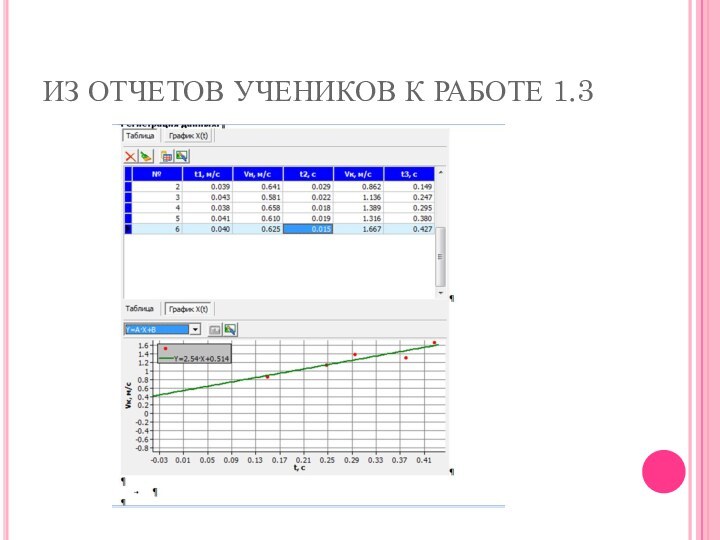
ИЗ ОТЧЕТОВ УЧЕНИКОВ К РАБОТЕ 1.3
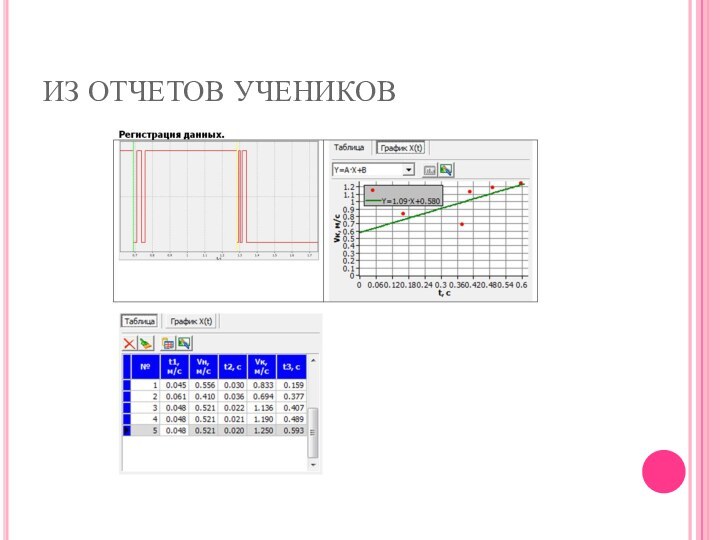
ИЗ ОТЧЕТОВ УЧЕНИКОВ
Лабораторная работа №
Тема: Исследование зависимости скорости равноускоренного движения от времени.
Цель работы: состоит в проверке утверждения о том, что скорость тела, движущегося равноускоренно по прямой, изменяется прямо пропорционально времени движения.
Оборудование:
- прибор для изучения прямолинейного движения;
- штатив с муфтой и перекладиной.
Указания к работе
Из определения ускорения следует, что скорость тела V, двигающегося прямолинейно с постоянным ускорением, спустя некоторое время t после начала движения может быть определена из уравнения: V = Vо + at (1). Если тело начало двигаться, не 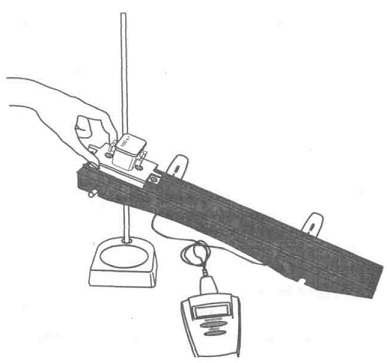
Чтобы проверить эти соотношения, необходимо определить значения скорости тела V1, V2 и V3, которые оно имело спустя промежутки времени t1, t2 и t3 после начала движения из состояния покоя.
Скорость в заданной точке траектории можно определить, зная перемещение тела из состояния покоя до этой точки и время движения. Действительно, при движении из состояния покоя (V0 = 0) с постоянным ускорением перемещение определяется по формуле S = at2/2, откуда a = 2S/t2 (4). после подстановки формулы (4) в (2): V = at = 2St/t2 и сокращения на t получают: V = 2S/t (5).
Для выполнения работы направляющую рейки устанавливают с помощью штатива в наклонном положении. Её верхний край должен находиться на высоте 18-20 см от поверхности стола. Под нижний край подкладывают пластиковый коврик. Каретку устанавливают на направляющей в крайнем верхнем положении, причём её выступ с магнитом должен быть обращен в сторону датчиков. Первый датчик размещают вблизи магнита каретки так, чтобы он запускал секундомер, как только каретка начнёт двигаться. Второй датчик устанавливают на удалении 20-25 см от первого. Далее работу выполняют в таком порядке:
1. Измеряют перемещение, которое каретка совершит, двигаясь между датчиками — S1.
2. Производят пуск каретки и измеряют время её движения между датчиками — t1.
3. Повторяют пуск каретки 6-7 раз, каждый раз записывая показания секундомера.
4. Вычисляют среднее время движения каретки t1cp по участку S1.
5. По формуле (5) определяют скорость, с которой двигалась каретка в конце первого участка: V1 = 2S1/t1ср.
б. Увеличивают расстояние между датчиками на 5см и повторяют серию опытов для измерения скорости тела в конце второго участка: V2 = 2S2/t2ср. Каретку в этой серии опытов, как и в первой, пускают из крайнего верхнего положения.
7. Проводят еще 2 серии опытов, увеличивая в каждой серии расстояние между датчиками на 5 см. Так находят значения скорости V3 и V4.
8. По полученным данным проверяют справедливость отношений: V2 : V1 = t2ср : t1ср, V3 : V2 = t3ср : t2ср и V4 : V2 = t4ср : t2ср
10. Строят график зависимости скорости от времени движения.
Оборудование:
прибор для изучения прямолинейного
движения
штатив.
Цель
работы состоит
в проверке утверждения о том, что скорость
тела, движущегося равноускоренно по
прямой, изменяется прямо пропорционально
времени движения.
Из
определения ускорения следует, что
скорость тела V,
двигающегося прямолинейно с постоянным
ускорением, спустя некоторое время t
после начала движения может быть
определена из уравнения: V
= V0
+ at
(1). Если тело начало двигаться, не имея
начальной скорости, то есть при V0
= 0, это
уравнение становится более простым: V
= at
(2). Отсюда следует, что тело, двигаясь
из состояния покоя с постоянным ускорением
a,
спустя время t1
с момента
начала движения, будет иметь скорость
V1
= at1,
спустя время t2
его скорость
будет V2
= at2,
спустя время
t3
— скорость
V3
= at3
и т.д. Причем, можно утверждать,
что
V2:
V1
= t2:
t1,
V3:
V1
= t3:
t1
и т.д. (3).
Чтобы
проверить эти соотношения, необходимо
определить значения скорости тела
V1
,V2
и V3,
которые оно имело спустя промежутки
времени t1,
t2
и t3
после начала движения из
состояния покоя.
Скорость
в заданной точке траектории можно
определить, зная перемещение тела из
состояния покоя до этой точки и время
движения. Действительно, при движении
из состояния покоя (V0
= 0) с
постоянным ускорением перемещение
определяется по формуле S=
,
откуда a
=
(4). После подстановки формулы (4) в (2):V
= a
t =
t и сокращения
на t
получают:
V
=
(5).
Для
выполнения работы направляющую рейки
устанавливают с помощью штатива в
наклонном положении. Ее верхний край
должен находиться на высоте 18-20 см от
поверхности стола. Под нижний край
подкладывают пластиковый коврик. Каретку
устанавливают на направляющей в крайнем
верхнем положении, причем ее выступ с
меткой должен быть обращен в сторону
датчиков. Первый датчик размещают вблизи
метки каретки так, чтобы он запускал
секундомер, как только каретка начнет
двигаться. Второй датчик устанавливают
на удалении 20-25 см от первого. Далее
работу выполняют в таком порядке.
-
Измеряют
перемещение, которое каретка совершит,
двигаясь между датчиками — S1. -
Производят
пуск каретки и измеряют время ее движения
между датчиками — t1. -
Повторяют
пуск каретки 6-7 раз, каждый раз записывая
показания секундомера. -
Вычисляют
среднее время движения каретки
t1
ср по
участку S1.
5.По
формуле (5) определяют скорость, с которой
двигалась каретка в конце первого
участка:
V1
=
.
6.Увеличивают
расстояние между датчиками на 5см и
повторяют серию опытов для измерения
скорости тела в конце второго участка:
V2
=
.
Каретку в этой серии опытов, как и в
первой, пускают из крайнего верхнего
положения.
7.Проводят
еще две серии опытов, увеличивая в каждой
серии расстояние между датчиками на 5
см. Так находят значения скорости
V3
и V4.
8.По
полученным данным проверяют справедливость
отношений:
9.V2
:V1
= t2
ср:t1
ср;
V3
: V2
= t3
ср
: t2
ср и
V4
:
V2
= t4
ср
: t2
ср.
10.Строят
график зависимости скорости от времени
движения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
26.04.2019907.26 Кб3МП.doc
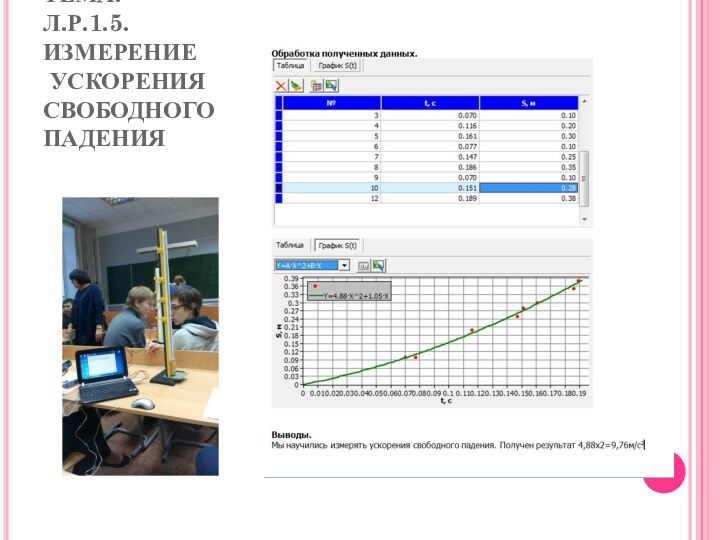
Лабораторная работа 1.4.
Исследование зависимости пути от времени при равноускоренном движении
Цель работы: установить зависимость пути от времени при равноускоренном движении и определить ускорение и начальную скорость движения тела.
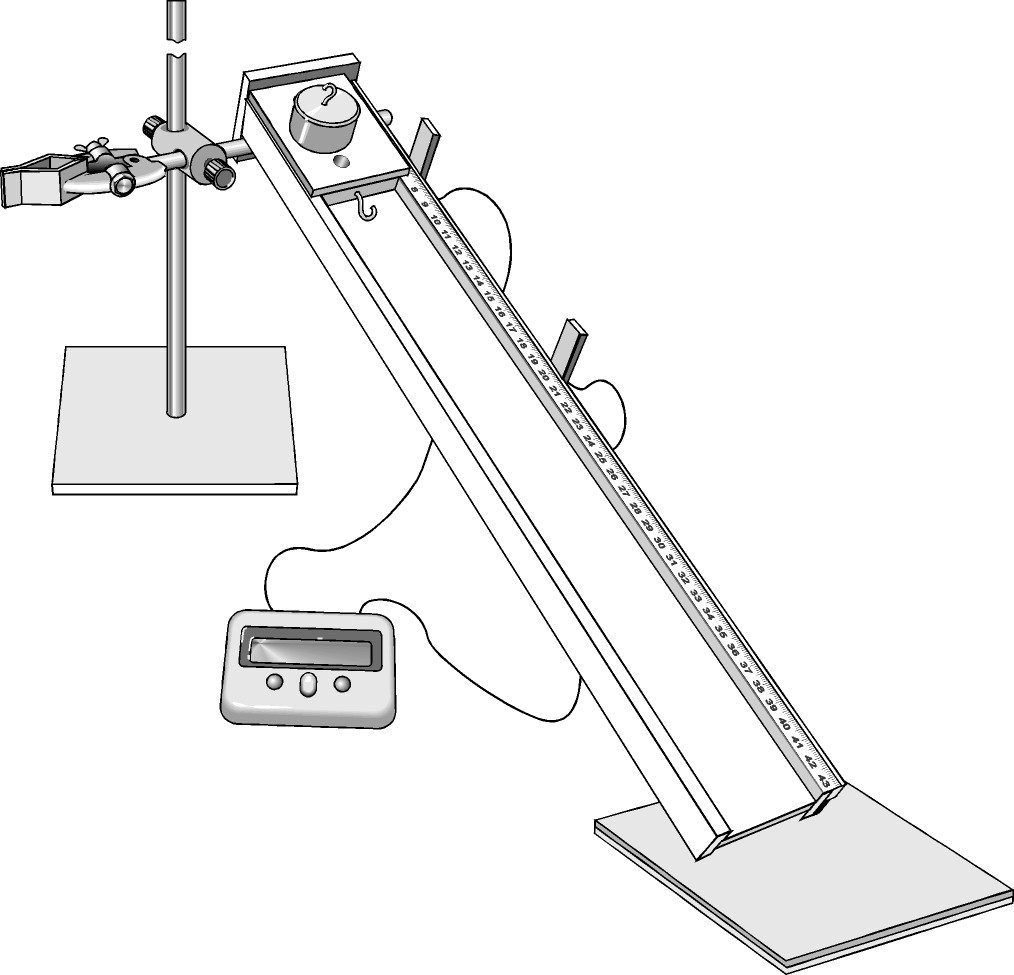
Оборудование: скамья, цифровой герконовый датчик положения, каретка с магнитом, коврик пенополиуретановый, муфта, нетбук с приложением «Практикум».
Ход работы
-
Соберите установку. Конец скамьи должен быть поднят примерно на 30 см, под нижний край положите пенополиуретановый коврик. 4 герконовых датчика устанавливаются на магнитной ленте на расстоянии 10 см друг от друга, начиная с отметки 20 см. Соедините герконы с USB-портом компьютера.
-
Запустите программу «Практикум». Выберите сценарий работы «1.4. Исследование зависимости пути от времени при равноускоренном движении».
-
Запустите измерения (кнопка
) и отпустите каретку с магнитом без начальной скорости. После достижения кареткой нижней точки остановите измерения (кнопка —
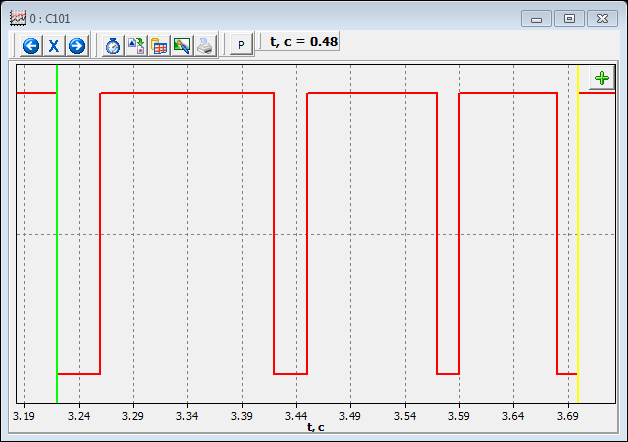
). Выделите и увеличьте область графика, содержащую 4 импульса (используя клавишу Alt).
-
Установите зеленый маркер в момент первого срабатывания первого геркона (кликните на рабочем поле в области начала первого всплеска правой кнопкой мыши для появления зеленого маркера) и измерьте промежутки времени от этого момента времени до начала срабатывания второго, третьего и четвертого герконов (левой кнопкой — в начале каждого всплеска). Каждый раз после установки желтого маркера нажимайте
и каждое нажатие на эту кнопку будет посылать значение выделенного маркерами интервала времени в следующую ячейку выбранного столбца Таблицы.
-
Выделите левой кнопкой нужную ячейку столбца «S, м», (кликнув на нее левой кнопки мыши, она окрасится в темно-голубой цвет) и введите в ячейку значение расстояния между первым и вторым герконом, (расстояния отмеряются по линейке на скамье). Заполните вторую и третью строку столбца значениями расстояний от первого геркона до третьего и четвертого герконов в метрах.
-
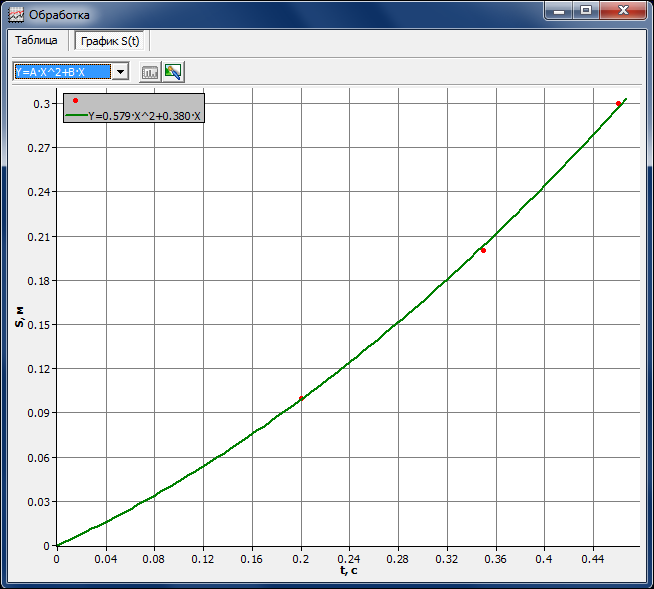
Перейдите на вкладку «График S(t)». Подберите функцию, которая наилучшим образом опишет полученный график (прямую вида Y=A·X2+BX). Постройте график функции на клавишу
.
-
Сравнивая коэффициенты уравнения с уравнением равноускоренного движения
, вычислите ускорение, с которым двигалась каретка, и скорость, с которой она двигалась мимо первого геркона.
-
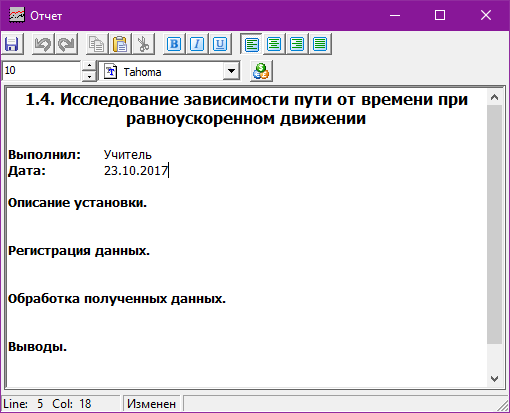
Для формирования отчета работы необходимо открыть (кнопка
) окно «Отчёт» и использовать меню, вызываемое по нажатию правой кнопки мыши после установки курсора в нужный блок отчета. Текстовые фрагменты отчета (например, Вывод) набираются с клавиатуры.
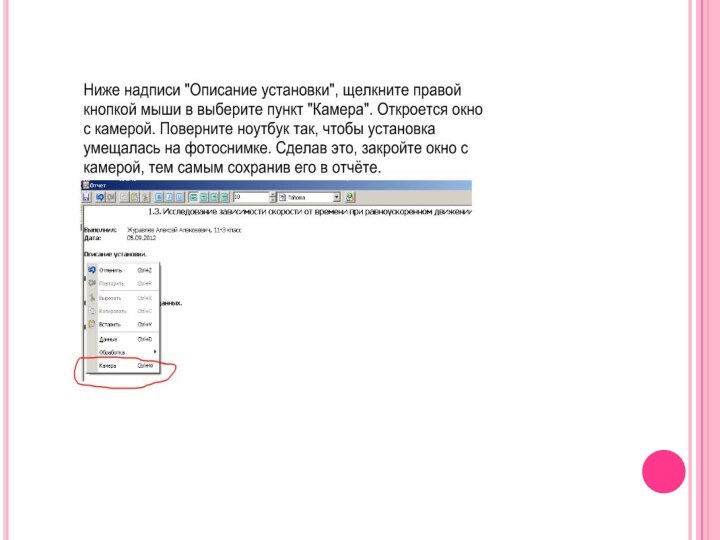
-
Используя в меню формирования Отчёта опцию «Камера» сфотографируйте вашу установку и поместите ее в отчет. Перенесите в Отчёт исходную кривую из «Окна регистрации», содержимое вкладок «Таблица» и «График». После подзаголовка «Выводы» запишите с клавиатуры вывод.
-
После создания Отчёт должен быть сохранен в директории указанной учителем в виде ФИО-1-4.rtf-файла.
Лабораторная работа 1.4. 1


Подборка по базе: дипломная работа Москаленко София 36-3 ВКР.docx, Практическая работа.docx, Контрольная работа.docx, Самостоятельная работа 3.1.3.docx, практическая работа 1.docx, Курсовая работа (геомеханика 2) Печенкин И.А..pdf, Практическая работа №3.docx, Проверочная работа по разделу.docx, Практическая работа_ХрамцоваЕ.pdf, Практическая работа №2.docx
Тольяттинский государственный университет
Институт математики, физики и информационных технологий
Кафедра «Общая и теоретическая физика»
Лабораторная работа № 1
« Исследование зависимости скорости от времени при равноускоренном движении»
Тольятти 2019
Лабораторная работа №1. «Исследование зависимости скорости от времени при равноускоренном движении»
Цель работы − исследовать зависимость скорости от времени движения тела.
Приборы и принадлежности: 1) рабочее поле, 2) штатив, 3) перекладина штатива, 4) наклонная плоскость, 5) каретка, 6) секундомер электронный с датчиками, 7) калькулятор.
3. Указания к самостоятельной работе
При подготовке к лабораторному занятию необходимо по методическим указаниям к данной лабораторной работе разобраться с выводом расчетной формулы к данной лабораторной работе.
Подготовиться к ответам на контрольные вопросы к данной лабораторной работе.
- Основные понятия кинематики
Любое физическое явление или процесс в окружающем нас материальном мире представляют собой закономерный ряд изменений, происходящих во времени и пространстве.
Механическое движение – простейший вид физического процесса, изучается в разделе физики, который называется механикой. Основная задача механики – определить положение тела в любой момент времени.
Механика – одна из самых древних наук. Определенные сведения в этой отрасли были известны еще в глубокой древности (Аристотель (IV в. до н.э.), Архимед (III в. до н.э.)). Количественное изучение механики началось только в XVII в., когда Г. Галилей (1564 – 1642) открыл кинематический закон сложения скоростей и установил законы свободного падения тел. Основные законы динамики сформулированы английским ученым И. Ньютоном (1643 – 1727).
В механике Ньютона движение тел рассматривается при скоростях много меньших скорости света в пустоте (вакууме). Эту механику называют классической или ньютоновской механикой. в отличие от релятивистской механики, созданной в начале XX в. главным образом благодаря работам А.Эйнштейна (1879 – 1956). В релятивистской механике движение тел рассматривают при скоростях, близких к скорости света.
Кинематикойназывают раздел механики, в котором движение тел рассматривается без выяснения причин, его вызывающих.
Механическим движением называется изменение положения тела в пространстве относительно других тел с течением времени.
Механическое движение относительно. Движение одного и того же тела относительно разных тел оказывается различным. Для описания движения тела нужно указать, по отношению к какому иному телу рассматривается движение. Это второе тело называют телом отсчета.
Система координат, связанная с телом отсчета и снабженная часами для измерения времени, образует систему отсчета.
Самая простая система координат – декартова система координат, три взаимно перпендикулярных оси – Оx, Оy,Оz.
В пространственной декартовой системе координат положение частицы задается ее координатами – x, y, z.
Система отсчета позволяет определять положение движущегося тела в любой момент времени.
В Международной системе единиц (СИ) за единицу длины принят метр (м), а за единицу времени – секунда (с).
Механика для описания движения тел в зависимости от условий конкретных задач использует разные физические модели. Простейшими физическими моделями являются: материальная точка – (МТ) и абсолютно твердое тело – (АТТ).
Всякое тело имеет определенные размеры. Если размеры тела малы по сравнению с расстоянием до других тел, то данное тело можно считать материальной точкой.
Материальная точка (МТ) – тело, размерами которого в условиях данной задачи можно пренебречь, считая что вся масса тела сосредоточена в одной точке. Так можно поступать, например, при изучении движения планет вокруг Солнца.
Макроскопическая частица (МЧ) – частица, образованная большим числом атомов.
Абсолютно твердое тело – тело, деформациями которого в условиях данной задачи можно пренебречь.
Движение тела, при котором все части тела движутся одинаково, называется поступательным.
Поступательно движутся, например, кабины в аттракционе «Колесо обозрения», автомобиль на прямолинейном участке пути и т. д. При поступательном движении тела его также можно рассматривать как материальную точку.
Перемещаясь с течением времени из одной точки пространства в другую, тело (материальная точка) описывает некоторую линию.
Траекториейдвижения тела (МТ) называется линия, которую тело (МТ) описывает при своем движении.
Положение материальной точки в пространстве можно определять с помощью закона движения – зависимости координат от времени:
| x=f(t), y=f(t), z=f(t). | (1.1) |
Такой способ описания движения называется координатным, а уравнения (1.1) – кинематическими уравнениями движения, заданными в координатной форме.
Исключив в соотношениях (1.1), записанных для движения МТ на плоскости xOy, зависимость от времени, получим уравнение траектории:
| y=f(x) | (1.2) |
Положение интересующей нас точки А в пространстве можно задать при помощи радиус −вектора 
Радиус-вектор 
При движении точки А ее радиус-вектор 
 =f(t), или =f(t), или
|
(1.3)
(1.4) |
Уравнения (1.3), (1.4) описывающие движение МТ с течением времени, называют кинематическими уравнениями движения МТ, заданными векторным способом.
Рис. 1.1. Радиус-вектор
На рис. 1.1. радиус-векторы 

Расстояние между начальной и конечной точками движения, отсчитанное вдоль траектории, называется длиной пройденного пути или путем – (обозначается S или l). Путь − величина скалярная.
Перемещением (

 |
(1.3) |
Перемещение − векторная величина, характеризуемая числовым значением и определенным направлением.
Рис. 1.2. Длина пройденного пути l, при движении от точки a до точки b, вектор перемещения
Если движение тела рассматривать в течение достаточно короткого промежутка времени, то вектор перемещения окажется направленным по касательной к траектории в данной точке, а его длина будет равна пройденному пути. При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути (рис. 1.2.).
Для характеристики неравномерного движения вводится понятие вектора средней скорости:
 |
(1.4) |
Вектор средней скорости ( 

Но больший интерес в физике представляет не средняя, а мгновенная скорость.
Мгновенная скорость определяется как предел, к которому стремится средняя скорость в течение бесконечно малого промежутка времени t:
 |
(1.5) |
Т. е., мгновенная скорость это скорость в данный момент времени (на рис.1.3 изображена синим цветом).
В математике такой предел называют производной и обозначают 

Мгновенная скорость тела (
 |
| Рис. 1.3. Средняя и мгновенная скорости
Н |
На рисунке 1.3. зеленым цветом показаны векторы перемещения 



 |
| Рис.1.4. Изменение вектора скорости по величине и направлению |
Изменение вектора скорости 



Этот вектор можно разложить на две составляющие:



Мгновенным ускорением 


| Рис. 1.5. Касательное, нормальное и полное ускорения |
 |
(1.6) |
Направление вектора ускорения 

Составляющие вектора ускорения 


 |
Касательное (тангенциальное) ускорение характеризует быстроту изменения модуля скорости тела:
 |
(1.7) |
Вектор 
Нормальное ускорениепоказывает, насколько быстро скорость тела изменяется по направлению.
Нормальное ускорение зависит от модуля скорости 

|
(1.8)
(1.9) |
Формула (1.8) определяет вектор, а (1.9) − величину (модуль) нормальной составляющей ускорения.
Вектор 
 |
(1.10) |
Криволинейное движение можно представить как движение по дугам окружностей (рис. 1.6.). Таким образом, основными физическими величинами в кинематике материальной точки являются: пройденный путь – l, перемещение –




Путь l величина скалярная, а перемещение –




 |
| Рис.1.6. Движение по дугам окружностей |
Равномерное движение
Простейшим видом механического движения является движение тела вдоль прямой линии с постоянной по модулю и направлению скоростью.
Такое движение называется равномерным. При равномерном движении тело за любые равные промежутки времени проходит равные пути.
Для кинематического описания равномерного прямолинейного движения координатную ось OX удобно расположить по линии движения. Положение тела при равномерном движении определяется заданием одной координаты x. Вектор перемещения и вектор скорости всегда направлены параллельно координатной оси OX. Поэтому перемещение и скорость при прямолинейном движении удобно спроектировать на ось OX и рассматривать их проекции как алгебраические величины.
Если в некоторый момент времени t1 тело находилось в точке с координатой x1, а в более поздний момент t2 – в точке с координатой x2, то проекция перемещения Δs на ось OX за время Δt = t2 – t1 равна:
|
(1.11) |
Эта величина может быть и положительной и отрицательной в зависимости от направления, в котором двигалось тело.
При равномерном движении вдоль прямой модуль перемещения совпадает с пройденным путем.
Скоростью равномерного прямолинейного движения называют отношение:
 |
(1.12) | |
Если υ > 0, то тело движется в сторону положительного направления оси OX; при υ < 0 тело движется в противоположном направлении.
Зависимость координаты x от времени t (закон движения) выражается при равномерном прямолинейном движении линейным математическим уравнением:
 , , |
(1.13) |
Где υ = const – скорость движения тела, x0 – координата точки, в которой тело находилось в момент времени t = 0. График закона движения x(t) представляет собой прямую линию. Примеры таких графиков показаны на рис. 1.7.
 |
| Рис. 1.7. Графики равномерного прямолинейного движения |
Для закона движения, изображенного на графике I (рис. 1.7.), при t = 0 тело находилось в точке с координатой x0 = –3. Между моментами времени t1 = 4 с и t2 = 6 с тело переместилось от точки x1 = 3 м до точки x2 = 6 м. Таким образом, за Δt = t2 – t1 = 2 с тело переместилось на Δs = x2 – x1 = 3 м. Следовательно, скорость тела составляет
Величина скорости оказалась положительной. Это означает, что тело двигалось в положительном направлении оси OX. Обратим внимание, что на графике движения скорость тела может быть геометрически определена как отношение сторон BC и AC треугольника ABC (см. рис. 1.7.):
 |
(1.14) |
Чем больше угол α, который образует прямая с осью времени, т. е. чем больше наклон графика (крутизна), тем больше скорость тела. Иногда говорят, что скорость тела численно равна тангенсу угла α наклона прямой x (t).
С точки зрения математики это утверждение не вполне корректно, так как стороны BC и AC треугольника ABC имеют разные размерности: сторона BC измеряется в метрах, а сторона AC – в секундах. Аналогичным образом для движения, изображенного на рис. 1.7. прямой II, найдем x0 = 4 м, υ = –1 м/с.
На рис. 1.8. закон движения x (t) тела изображен с помощью отрезков прямых линий. В математике такие графики называются кусочно-линейными. Такое движение тела вдоль прямой не является равномерным. На разных участках этого графика тело движется с различными скоростями, которые также можно определить по наклону соответствующего отрезка к оси времени. В точках излома графика тело мгновенно изменяет свою скорость. На графике (рис. 1.8.) это происходит в моменты времени t1 = –3 с, t2 = 4 с, t3 = 7 с и t4 = 9 с. По графику движения нетрудно найти, что на интервале (t2; t1) тело двигалось со скоростью υ12 = 1 м/с, на интервале (t3; t2) – со скоростью υ23 = –4/3 м/с и на интервале (t4; t3) – со скоростью υ34 = 4 м/с.
Следует отметить, что при кусочно-линейном законе прямолинейного движения тела пройденный путь l не совпадает с перемещением s. Например, для закона движения, изображенного на рис. 1.8, перемещение тела на интервале времени от 0 с до 7 с равно нулю (s = 0). За это время тело прошло путь l = 8 м.
 |
| Рис. 1.8. Кусочно-линейный закон движения |
Равноускоренное движение
В общем случае равноускоренным движением называют такое движение, при котором вектор ускорения 

Тогда криволинейное движение камня можно представить как сумму двух простых движений – прямолинейного равноускоренного движения вдоль оси OY и равномерного прямолинейного движения в перпендикулярном направлении, т. е. вдоль оси OX (рис. 1.9.).
Таким образом, изучение равноускоренного движения сводится к изучению прямолинейного равноускоренного движения. В случае прямолинейного движения векторы скорости 

 |
Рис. 1.9. Проекции векторов скорости  и ускорения и ускорения  на координатные оси. ax = 0, ay = –g. на координатные оси. ax = 0, ay = –g. |
При равноускоренном прямолинейном движении скорость тела определяется формулой:
 |
(1.15) |
В этой формуле υ0 – скорость тела при t = 0 (начальная скорость), a = const – ускорение. На графике скорости υ (t) эта зависимость имеет вид прямой линии (рис. 1.10).
 |
| Рис. 1.10. Графики скорости равноускоренного движения |
По наклону графика скорости может быть определено ускорение a тела.
Соответствующие построения выполнены на рис. 1.10. для графика I. Ускорение численно равно отношению сторон треугольника ABC:
 |
(1.16) |
Чем больше угол β, который образует график скорости с осью времени, т. е. чем больше наклон графика (крутизна), тем больше ускорение тела.
Для графика I: υ0 = –2 м/с, a = 1/2 м/с2.
Для графика II: υ0 = 3 м/с, a = –1/3 м/с2.
График скорости позволяет также определить проекцию перемещения s тела за некоторое время t. Выделим на оси времени некоторый малый промежуток времени Δt. Если этот промежуток времени достаточно мал, то и изменение скорости за этот промежуток невелико, т. е. движение в течение этого промежутка времени можно считать равномерным с некоторой средней скоростью, которая равна мгновенной скорости υ тела в середине промежутка Δt. Следовательно, перемещение Δs за время Δt будет равно Δs = υΔt. Это перемещение равно площади заштрихованной полоски (рис. 1.10). Разбив промежуток времени от 0 до некоторого момента t на малые промежутки Δt, получим, что перемещение s за заданное время t при равноускоренном прямолинейном движении равно площади трапеции ODEF. Соответствующие построения выполнены для графика II на рис. 1.10. Время t принято равным 5,5 с.
Так как υ – υ0 = at, окончательная формула для перемещения s тела при равноускоренном движении на промежутке времени от 0 до t запишется в виде:
 |
(1.17) |
Для нахождения координаты y тела в любой момент времени t нужно к начальной координате y0 прибавить перемещение за время t:
 |
(1.18) |
Выражение (1.18.) называют законом равноускоренного движения.
При анализе равноускоренного движения иногда возникает задача определения перемещения тела по заданным значениям начальной υ0 и конечной υ скоростей и ускорения a. Эта задача может быть решена с помощью уравнений, написанных выше, путем исключения из них времени t. Результат записывается в виде:
 |
(1.19.) |
Из этой формулы(1.18.) можно получить выражение для определения конечной скорости υ тела, если известны начальная скорость υ0, ускорение a и модуль перемещения s:
 |
(1.20.) |
Если начальная скорость υ0 равна нулю, формулы (1.19) и (1.20) принимают вид:
 . . |
(1.21.) |
Следует еще раз обратить внимание на то, что входящие в формулы равноускоренного прямолинейного движения величины υ0, υ, s, a, y0 являются величинами алгебраическими. В зависимости от конкретного вида движения каждая из этих величин может принимать как положительные, так и отрицательные значения.
5.Фото и описание экспериментальной установки
Экспериментальная установка для исследования зависимости скорости от времени при равноускоренном движении собирается из:
- штатива, 2) перекладины штатива, 3) наклонной плоскости, 4) каретки, 5) секундомера электронного с датчиками.

Рис.1.12. Экспериментальная установка для исследования зависимости скорости от времени при равноускоренном движении
6. Порядок выполнения работы
1. Соберите установку для исследования равноускоренного скольжения каретки (бруска) по наклонной плоскости. Установите наклонную плоскость под углом 30 к горизонту, используя штатив, и перекладину к штативу и транспортир.
2. Зарисуйте схематично экспериментальную установку с обязательным указанием на наклонной плоскости положений датчиков – «верхнего» и «нижнего» и каретки между ними.
3. Проведите 5 опытов по измерению времени t движения каретки и пройденного пути s = x – x0 (в единицах СИ), каждый раз изменяя положение «нижнего» датчика, т. е. пройденный путь каретки. Результаты измерений занесите в таблицу бланка отчета.
4. Выведите формулы для расчета: 1) скорости; 2) ускорения равноускоренного движения, воспользовавшись теоретическим материалом раздела 1. Механика.
5. Произведите расчеты скорости 

6. Рассчитайте среднее значение ускорения движения тела 
7. Составьте уравнение математической зависимости скорости каретки от времени, имеющей общий вид: 
8. Постройте по данным эксперимента график зависимости V=f(t) и объясните его.
9. Сделайте выводы
7. Контрольные вопросы
- Какой раздел механики называют кинематикой?
- Какое движение называют механическим?
- Какое тело называют телом отсчета?
- Что называют системой отсчета?
- В каких единицах в СИ измеряют: 1) промежуток времени; 2) длину пути; 3) скорость движения; 4) ускорение тела?
- Какая система тел называется механической?
- Перечислите виды равнопеременного движения.
- Запишите определение вектора средней скорости.
- Запишите определение вектора мгновенной скорости.
- Какая составляющая ускорения называется касательной (тангенциальной) составляющей?
- Каково направление касательной (тангенциальной) составляющей ускорения?
- Какая составляющая ускорения называется нормальной составляющей?
- Каково направление нормальной составляющей ускорения?
- Запишите определение равноускоренного движения.
- Запишите формулу, определяющую:
1) величину конечной скорости при равноускоренном движении;
2) закон равноускоренного движения;
3) модуль тангенциальной составляющей ускорения;
4) модуль нормальной составляющей ускорения;
5) модуль полного ускорения при криволинейном движении.
Слайд 1
ЛАБОРАТОРНАЯ РАБОТА №1
1.3 ЭЛЕКТРОННЫЙ ОТЧЕТ , СТР. 20
ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ СКОРОСТИ
ОТ ВРЕМЕНИ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ
Слайд 2
ЦЕЛИ РАБОТЫ:
1) Научиться пользоваться лабораторным комплексом «Цифровая лаборатория»
2) Исследовать движение
бруска по наклонной плоскости
Слайд 3
ОБОРУДОВАНИЕ:
1) Штатив с муфтой
2) Линейка магнитная
3) Герконовые датчики
4) Ноутбук с
программным обеспечением
5) Деревянный блок
Слайд 4
ЗАКРЕПИТЕ ЛИНЕЙКУ НА ШТАТИВЕ
Слайд 5
Штатив поднимите на высоту не менее 30 см
Под нижний край
линейки положите поролоновый коврик
Слайд 6
ОБРАТИТЕ ВНИМАНИЕ!
Вначале надо подключить датчик, а потом открыть программу
Слайд 7
Установите на линейку герконовые датчики: первые два — вплотную на
отметке 15 см, вторые два — вплотную на отметке 25 см.
Слайд 8
Слайд 9
Слайд 10
Слайд 11
Слайд 12
Слайд 13
Слайд 14
Получив 4 импульса, вы уже можете использовать их
в качестве первых измерений:
1) Увеличьте область графика, содержащую
4 импульса.
2) Измерьте участок графика, соединяющий начало 1 и начало 2 импульса.
Слайд 15
Слайд 16
Слайд 17
Слайд 18
Слайд 19
ПОЛУЧИВ ВСЕ ДАННЫЕ, СМЕСТИТЕ ВТОРУЮ ПАРУ ГЕРКОНОВ НА 7 СМ
В СТОРОНУ ОТ ПЕРВОЙ ПАРЫ ГЕРКОНОВ (НА ОТМЕТКУ 32 СМ)
Слайд 20
Слайд 21
Слайд 22
Слайд 23
Слайд 24
ПОЛУЧЕН ГРАФИК ФУНКЦИИ V(T).
ЗАПИШИТЕ КОЭФФИЦИЕНТЫ А И В ПРЯМОЙ, ПОДУМАЙТЕ
НАД ИХ ФИЗИЧЕСКИМ СМЫСЛОМ
Слайд 25
СОСТАВЛЕНИЕ ОТЧЕТА
Слайд 26
Слайд 27
Слайд 28
СОСТАВЛЕНИЕ ОТЧЕТА
Слайд 29
СОСТАВЛЕНИЕ ОТЧЕТА
Слайд 30
ВЫВОДЫ
В выводе ответьте на следующие вопросы:
1) Как двигался брусок во
время эксперимента?
2) Чему были равны начальная скорость (скорость при прохождении первой пары герконов) и ускорение бруска (из графика)?
3) Для чего 1 и 2, а также 3 и 4 герконы были установлены вплотную друг к другу?
Слайд 31
СОХРАНЕНИЕ ОТЧЕТА
Слайд 32
ИЗ ОТЧЕТОВ УЧЕНИКОВ К РАБОТЕ 1.3
Слайд 33
ИЗ ОТЧЕТОВ УЧЕНИКОВ
Слайд 34
СЛЕДУЮЩАЯ ТЕМА:
Л.Р.1.5. ИЗМЕРЕНИЕ
УСКОРЕНИЯ
СВОБОДНОГО
ПАДЕНИЯ
Исследование зависимости пути от времени при равноускоренном движении без начальной скорости.
Поучаствуйте в проекте и получите знак отличия.
Механическое движение — это изменение положение тела с течением времени. Первым учёным, проводившим экспериментальные исследования различных видов механического движения, был Галилео Галилей (рубеж XVI и XVII веков). До Галилея изучение природы было чисто философским, никаких измерений не проводилось. Одной из причин этого являлось отсутствие точных приборов для измерения времени. По часам в XVI веке можно было измерять собственно часы, но не минуты и не секунды. Поэтому Галилей для измерения времени использовал собственный пульс.
Один из распространённых видов механического — прямолинейное равноускоренное движение. Для его исследования можно спускать брусок по наклонной плоскости, что мы и проделаем в данной лабораторной работе.
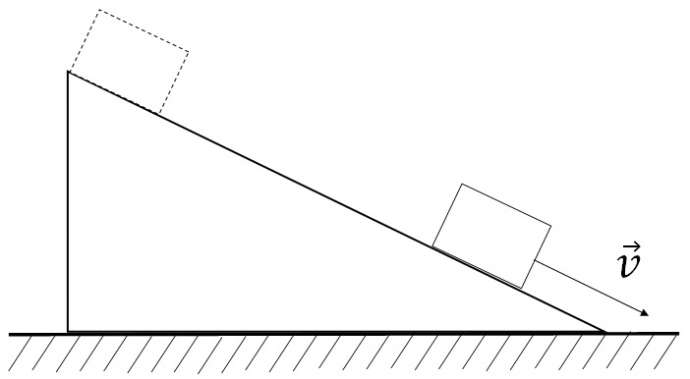
Галилей исследовал прямолинейное равноускоренное движение без начальной скорости. Он измерял расстояние, которое брусок при соскальзывании по наклонной плоскости преодолевает за одну, две, три, четыре секунды. При этом он установил, что расстояние, которое проходит брусок за 1, 2, 3, 4 секунды пропорциональны квадратам этих чисел (1, 4, 9, 16). Т. е. за 2 секунды брусок проходит путь в 4 раза больший, чем за одну секунду. За 3 секунды — в 9 раз больший, чем за одну секунду и т. д. То есть путь при прямолинейном равноускоренном движении без начальной скорости пропорционален квадрату времени. Позднее в виде формулы эта зависимость была записана в таком виде:
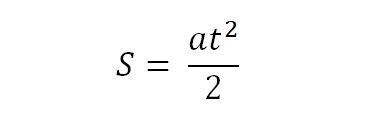
Давайте повторим эксперимент великого итальянца и выясним, действительно ли верна установленная им закономерность?



































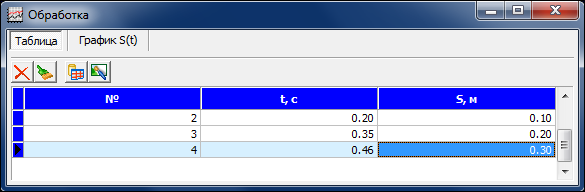
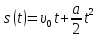 , вычислите ускорение, с которым двигалась каретка, и скорость, с которой она двигалась мимо первого геркона.
, вычислите ускорение, с которым двигалась каретка, и скорость, с которой она двигалась мимо первого геркона.