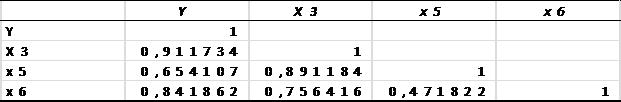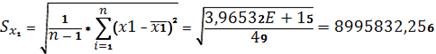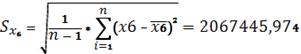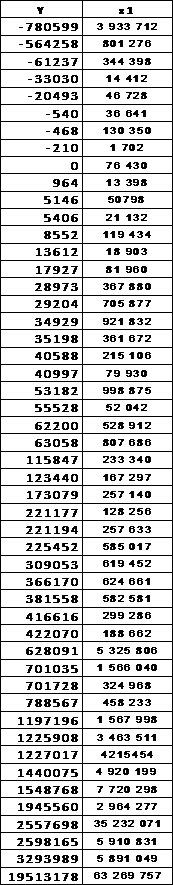Из
корреляционного анализа было видно,
что самый сильный фактор,
оказывающий
влияние на Y
(Прибыль), фактор Х3 Основные
средства.
По этому фактору строим Регрессию с
помощью инструмента Регрессия
в
Анализе данных (рис.
8):


Рисунок
9. Получение табличного значения
F-критерия
-
Оценка качества построенной модели
Для
оценки качества модели определим
коэффициент детерминации. Значение
коэффициента детерминации можно найти
в таблице Регрессионный
анализ
(см. рис. 8).
R2
=
0,827.
Коэффициент
детерминации показывает долю вариации
результативного признака под воздействием
изучаемых факторов. Следовательно,
около 88% вариации зависимой переменной
учтено в модели и обусловлено влиянием
факторов, включенных в модель.
Точность
модели оценим с помощью средней ошибки
аппроксимации:
А
= 1/n
(рис. 10)

Рисунок
10. Определение точности модели.
Проверку
значимости уравнения регрессии оценим
с помощью F-критерия
Фишера:
F
=

Значение
F-критерия
Фишера можно найти в таблице Дисперсионный
анализ
протокола Excel
(см. рис. 8). F
=230,99.
Поскольку
Fрасч
> Fтабл,
уравнение регрессии следует признать
значимым, то есть его можно использовать
для анализа и прогнозирования.

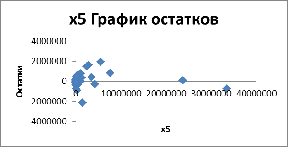
Рисунок
11. Графики остатков по каждому из факторов
Из
графиков, представленных на рисунке 11
видно, что дисперсия остатков более
всего нарушена по отношению к фактору
Краткосрочные
обязательства.
-
Ранжирование компаний по степени эффективности.
Используя
результаты регрессионного анализа,
выполним ранжирование компаний по
степени эффективности. Для этого
воспользуемся функцией Анализ данных
– регрессия – за входной интервал Y
мы возьмем все значения по Y,
а за входной интервал Х мы возьмем все
значения по факторам Х2, Х3 и Х6 – выведем
остатки – ок. Далее сортируем столбцы
«Наблюдение»,
«Предсказанное Y»
и «Остатки» по
остаткам (рис. 12).
Рисунок
12. Ранжирование компаний по эффективности
Вывод:
Самый отрицательный остаток у компании
ОАО Нефтегазовая компания «Славнефть»
— самая неэффективная компания.
9.
Составление уравнений нелинейной
регрессии:
-
А.
гиперболической; -
Б.
степенной; -
В.
Показательной.
Для
построения уравнений нелинейной
регрессии нам нужно выполнить следующие
действия (выполняем по фактору Х3, рис.
13):

Рисунок
13. Данные фактора Х3
-
Выделяем
значения факторов Y
и Х3 – сортировка – по Y. -
Выделяем
другим цветом убыточные предприятия
и копируем рядом прибыльные – сортировка
– по Х3 (рис. 14).
Рисунок
14. Сортировка по фактору Y
и выделение отдельно
прибыльных
компаний по фактору Х3.
с.Далее
в новом столбце считаем 1/Х, LNX
и LNY
(рис. 15).

Рисунок
15. Данные для построения уравнений
нелинейных регрессий
Теперь
можно строить гиперболическую, степенную
и показательную модели нелинейной
регрессии.
-
Гиперболическая:
Анализ
данных – регрессия – входной интервал
Y
— весь Y,
входной
интервал
X-
1/Х – ок. R-квадрат
= 0,72–означает, что прогноз по данной
модели делать нельзя (рис. 16).
Нелинейная
степенная.(рис.16)

Нелинейная
показательная.(рис 17)


Вывод:
нелинейную гиперболическую модель
нельзя использовать при прогнозировании.
Прогноз можно осуществить либо по
нелинейной степенной модели, т.к.
R-квадрат
(степ.) > R-квадрат
(показ.), либо по двухфакторной модели
с факторами Х3 и Х4.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Построение регрессионной модели экономической деятельности компаний нефтегазовой отрасли
Федеральное
государственное образовательное бюджетное учреждение высшего профессионального
образования
Финансовый
университет при Правительстве Российской Федерации
Владимирский
филиал финансового университета
Заочный
факультет экономики
Кафедра
«Математика и информатика»
Контрольная
работа
По
дисциплине «Эконометрика»
Студент:
Ашуралиев Ф.Х.
Курс: 3,
группа: ЗБ3-ЭК301
Преподаватель:
Бутковский О.Я.
Владимир
2015
На основании данных, приведенных в табл. 1:
. Постройте диаграммы рассеяния, представляющие
собой зависимости Y от каждого из факторов Х. Сделайте выводы о характере
взаимосвязи переменных.
. Осуществите двумя способами выбор факторных
признаков для построения регрессионной модели:
а) на основе анализа матрицы коэффициентов парной
корреляции, включая проверку гипотезы о независимости объясняющих переменных
(тест на выявление мультиколлинеарности Фаррара-Глоубера);
б) с помощью пошагового отбора методом
исключения.
. Постройте уравнение множественной регрессии в
линейной форме с выбранными факторами. Дайте экономическую интерпретацию
коэффициентов модели регрессии.
4. Дайте сравнительную оценку силы
связи факторов с результатом с помощью коэффициентов эластичности, и ∆коэффициентов.
. Рассчитайте параметры линейной
парной регрессии для наиболее подходящего фактора Хj.
. Оцените качество построенной
модели с помощью коэффициента детерминации, средней относительной ошибки
аппроксимации и F-критерия Фишера.
. Проверьте выполнение условия
гомоскедастичности.
. Используя результаты
регрессионного анализа, ранжируйте компании по степени эффективности.
. Осуществите прогнозирование
среднего значения показателя Y при уровне значимости = 0,1, если прогнозное значение
фактора Хj составит 80% от его максимального значения. Представьте на графике
фактические данные Y, результаты моделирования, прогнозные оценки и границы
доверительного интервала.
. Составьте уравнения нелинейной
регрессии:
а) гиперболической;
б) степенной;
в) показательной.
. Приведите графики построенных
уравнений регрессии.
. Для нелинейных моделей найдите
коэффициенты детерминации и средние относительные ошибки аппроксимации.
Сравните модели по этим характеристикам и сделайте вывод о лучшей модели.
Таблица
1
|
Добыча |
№ |
Прибыль |
Оборотные |
Дебиторская |
Запасы |
|
Y |
X3 |
х5 |
х6 |
||
|
Аганнефтегазгеология, |
1 |
1440075 |
4 |
3490541 |
31365 |
|
Азнакаевский |
2 |
5146 |
50798 |
23014 |
0 |
|
Акмай, |
3 |
13612 |
18 |
8678 |
84 |
|
Аксоль, |
4 |
964 |
13 |
4821 |
0 |
|
Акционерная |
5 |
19513178 |
63 |
23780450 |
1696853 |
|
АЛРОСА |
6 |
28973 |
367 |
204181 |
19474 |
|
Арктическая |
7 |
-780599 |
3 |
1456438 |
176 |
|
Барьеганнефтегаз, |
8 |
2598165 |
5 |
5566412 |
127937 |
|
Белкамнефть, |
9 |
628091 |
5 |
4285041 |
73823 |
|
Белорусское |
10 |
29204 |
705 |
624393 |
130 |
|
Битран, |
11 |
1945560 |
2 |
2918345 |
39667 |
|
Богородскнефть, |
12 |
366170 |
624 |
484537 |
5733 |
|
Братскэкогаз, |
13 |
-20493 |
46 |
9865 |
3319 |
|
Булгарнефть, |
14 |
381558 |
582 |
196045 |
5763 |
|
Варьеганнефть, |
15 |
1225908 |
3 |
1095263 |
430844 |
|
Верхнечонскнефтегаз, |
16 |
3293989 |
5 |
2477424 |
38133 |
|
Восточная |
17 |
416616 |
299 |
48174 |
28393 |
|
Восточно-Сибирская |
18 |
-564258 |
801 |
286058 |
236642 |
|
Геологоразведочный |
19 |
221194 |
257 |
72854 |
4548 |
|
ГРОЗНЕФТЕГАЗ, |
20 |
701035 |
1 |
1304084 |
8773 |
|
Губкинский |
21 |
62200 |
528 |
294575 |
0 |
|
ДАГНЕФТЕГАЗ, |
22 |
123440 |
167 |
44889 |
24866 |
|
Елабуганефть, |
23 |
55528 |
52 |
24275 |
3949 |
|
Иделойл, |
24 |
422070 |
188 |
140535 |
8212 |
|
Избербашнефть, |
25 |
-468 |
130 |
114444 |
940 |
|
ИНВЕСТИЦИОННАЯ |
26 |
225452 |
585 |
272147 |
0 |
|
Инга, |
27 |
-61237 |
344 |
76561 |
11218 |
|
КАББАЛКНЕФТЕТОППРОМ, |
28 |
-540 |
36 |
25017 |
127 |
|
Калининграднефть, |
29 |
40588 |
215 |
18072 |
7569 |
|
КАМЧАТГАЗПРОМ, |
30 |
53182 |
998 |
496994 |
0 |
|
Кировское |
31 |
-210 |
1 |
602 |
46 |
|
Когалымнефтепрогресс, |
32 |
63058 |
807 |
474612 |
0 |
|
Комнедра, |
33 |
1197196 |
1 |
1040387 |
25862 |
|
Кондурчанефть, |
34 |
221177 |
128 |
55155 |
1260 |
|
Корпорация |
35 |
1548768 |
7 |
7613662 |
14716 |
|
Краснодарское |
36 |
-33030 |
14 |
5038 |
0 |
|
Ленинградсланец, |
37 |
34929 |
921 |
61353 |
833099 |
|
Меллянефть, |
38 |
115847 |
233 |
122062 |
6824 |
|
МНКТ, |
39 |
35198 |
361 |
168314 |
3227 |
|
Мохтикнефть, |
40 |
788567 |
458 |
317153 |
14021 |
|
Научно-производственное |
41 |
309053 |
619 |
212882 |
1909 |
|
Научно-производственное |
42 |
8552 |
119 |
63550 |
2558 |
|
НГДУ |
43 |
173079 |
257 |
147549 |
16197 |
|
НЕГУСНЕФТЬ, |
44 |
1227017 |
4215454 |
171162 |
63810 |
|
НЕНЕЦКАЯ |
45 |
701728 |
324 |
237083 |
3886 |
|
НЕФТЕБУРСЕРВИС, |
46 |
17927 |
81 |
73343 |
963 |
|
Нефтегазовая |
47 |
2557698 |
35 |
33477251 |
26578 |
|
Нефтеразведка, |
48 |
0 |
76 |
15161 |
7 |
|
Нефть, |
49 |
5406 |
21 |
7540 |
6465 |
|
Нефтьинвест, |
50 |
40997 |
79 |
58762 |
1035 |
1. Постройте диаграммы рассеяния, представляющие
собой зависимости Y от каждого из факторов Х. Сделайте выводы о характере
взаимосвязи переменных
Построенные диаграммы рассеяния, зависимости Yот
X3 (рис.1), от X5
(рис. 2), от X6 (рис.3). По
характеру распределения данных, можно сделать предположение, что существует
некоторая тенденция прямой линейной связи между значениями объясняемой
переменной и факторами X3
и X5 и отсутствия с
фактором X6.
Рис. 1
Рис. 2
Рис. 3
. Осуществите двумя способами выбор факторных
признаков для построения регрессионной модели
а) на основе анализа матрицы коэффициентов
парной корреляции, включая проверку гипотезы о независимости объясняющих переменных
(тест на выявление мультиколлинеарности Фаррара-Глоубера);
Таблица
2
Анализ матрицы коэффициентов парной корреляции
начинаем с ее первого столбца, где расположены коэффициенты корреляции,
отражающие тесноту связи зависимой переменной Y
“прибыль (убыток)” с включенными в анализ факторами. Анализ показывает, что
зависимая переменная Y,
имеет тесную связь с долгосрочными обязательствами (ry,x3
= 0,912) и с запасами готовой продукции для перепродажи (ry,x6=
0,842). Фактор Х5имеет слабую связь с зависимой переменной и его не
рекомендуется включать в модель (исключим его в пошаговом методе).
Затем переходим к анализу остальных столбцов
матрицы с целью выявления мультиколлинеарности. Факторы X1и
X6нетесно
связаны между собой (rx3,x6=
0,756), что не свидетельствует о наличии мультиколлинеарности.
Таким образом, на основе анализа только
корреляционной матрицы остаются два фактора — Долгосрочные обязательства и
Запасы готовой продукции для перепродажи (n = 50, k =2).
. Проверка наличия мультиколлинеарности всего
массива переменных
Построим матрицу межфакторных корреляций R1
(табл. 4.3) и найдем ее определитель det [R1] = 0,373 с помощью функции МОПРЕД.
Таблица
3
Вычислим наблюдаемое значение статистики Фаррара
— Глоубера по формуле:
=-((50-1-(1/6)*(2*3+5))*(-0,37)
= 17,5
где n
= 50 — количество наблюдений;
k = 3 -количество
факторов.
Фактическое значение этого критерия FGнабл
сравниваем с табличным значением X2c
1/2k(k-1)
= 3 степенями свободы и уровнем значимости α=0,05. Табличное
значение X2
находим с помощью функции ХИ2.ОБР.ПХ. FGкр
= 0,352.
Так как FGнабл>FGкр
(17,5>0,352), следовательно в массиве объясняющих переменных существует
мультиколлинеарность.
б) с помощью пошагового отбора методом исключения.
Пошаговый отбор методом исключения. Построение
модели регрессии с помощью инструмента Регрессия (Анализ данных в Excel)
приведено в таблице 4.
-й шаг — модель регрессии по всем факторам:
Таблица
4
Линейное уравнение трехфакторной модели
регрессии имеет вид:
Проверим значимость коэффициентов
парной корреляции по критерию Стьюдента. Расчетное значение критерия Стьюдента
приведены в графе t-статистика.
Для параметра 
— параметр
при факторе
Для параметра 
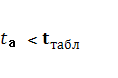
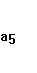
Для параметра 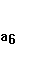
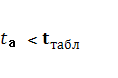
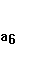
Исключаем фактор Х5.
2-й шаг
— модель регрессии по двум факторам:
Таблица
5
Линейное уравнение двухфакторной модели
регрессии имеет вид:
Проверим значимость коэффициентов
парной корреляции по критерию Стьюдента. Расчетное значение критерия Стьюдента
приведены в графе t-статистика.
Для параметра 
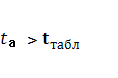
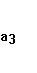
Для параметра 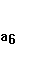
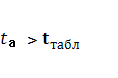
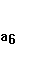
3. Постройте уравнение множественной регрессии в
линейной форме с выбранными факторами. Дайте экономическую интерпретацию
коэффициентов модели регрессии
На основании пункта 2.б из модели фактор X2
исключаем, тогда уравнение зависимости прибыли (убытка) можно записать в
следующем виде:
Уравнение регрессии показывает,
каково будет в среднем значение переменной , если переменные X примут
конкретные значения.
коэффициент
регрессии aj показывает,
на какую величину в среднем изменится результативный признак Y, если
переменную xj увеличить на единицу измерения, т.е. aj является
нормативным коэффициентом.
В данном случае =0,179
показывает, что при увеличении долгосрочной задолженности на 1 тыс. руб.
прибыль увеличится на 179 тыс. руб.
В данном случае а3=3,172показывает,
что при увеличении запасов готовой продукции для перепродажи на 1 тыс. руб.
прибыль увеличится на 3712 тыс. руб.
. Дайте сравнительную оценку силы
связи факторов с результатом с помощью коэффициентов эластичности, и ∆коэффициентов
факторный регрессионный
экономический матрица
Учитывая, что коэффициент регрессии
невозможно использовать для непосредственной оценки валяния факторов на
зависимую переменную из-за различия единиц измерения и разной колеблемости
факторов, используем коэффициенты эластичности, бета- и дельта- коэффициенты.
Для коэффициента регрессии вычислим
коэффициент эластичности и бета-коэффициент по формулам:
0,147´2321364,22/842311,451=0,388099821
Прибыль увеличится на 38,81%, если
фактор долгосрочные обязательства увеличатся на 1%.
4,274´76620,02/842311,451=0,1739
Прибыль увеличится на 17,39%, если фактор запасы
готовой продукции увеличатся на 1%.
a) -коэффициент:
Коэффициент показывает, что при увеличении
долгосрочных обязательств 
8995832,256 тыс. руб. Прибыль увеличится на 1322387,342 тыс. руб.
(0,47*2813269,802)
Коэффициент показывает, что при увеличении
запасов готовой продукции для перепродажи на 72567008373 тыс. руб. Прибыль
увеличится на 3,10151E+11 тыс. руб. (0,039*2813269,802)) -коэффициент:
Вывод: изменение результата У (прибыль)
происходит под влиянием фактора (долгосрочные обязательства), включенного в
модель, на 47%.
Изменение результата У (прибыль) происходит под
влиянием фактора (запасы готовой продукции), включенного в модель, на 3,7%.
. Рассчитайте параметры линейной парной
регрессии для наиболее подходящего фактора Хj
В нашем случае это фактор Х1 (долгосрочные
обязательства)
Таблица
5
Линейное уравнение трехфакторной модели
регрессии имеет вид:
6. Оценка качества построенной модели через
коэффициент детерминации, средней относительной ошибки аппроксимации и F
— критерия Фишера
Для оценки качества модели множественной
регрессии вычисляют коэффициент множественной корреляции Rи
коэффициент детерминации R2.
Значение коэффициентов детерминации и множественной корреляции можно вычислить
по формулам:
Коэффициент детерминации R2
(R-квадрат):
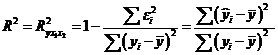
где у ̅ — среднее значение
определяемой переменной,
а у̂ — расчетное значение
определяемой переменной.
Коэффициент детерминации можно найти
в результатах регрессионного анализа (табл. 5).
Он показывает долю вариации
результативного признака под воздействием изучаемых факторов. Следовательно,
около 83,1% вариации зависимой переменной учтено в модели и обусловлено
влиянием включенного фактора.
Коэффициент множественной
корреляции, индекс корреляции (множественный R):
= 0,912
Он показывает высокую тесноту связи
зависимой переменной Y с включенным в модель
объясняющим фактором.
Проверка значимости уравнения регрессии
производится на основе вычисления F
— критерия Фишера:
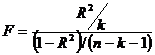
((1-0,831)/(50-1-1)) = 236,46,
где n — количество наблюдений (компаний);
а k — количество факторов (переменных анализа).
Расчетное значение F
— критерия берем из результатов регрессионного анализа (табл. 5).
Табличное значение F
— критерия при доверительной вероятности 0,95 при v1
= k = 1 и v2
= n — k
— 1 = 50 — 1 — 1 = 48 составляет 4,04. Табличное значение F
— критерия можно найти с помощью функции F.
Поскольку F>F
, уравнение
регрессии следует признать значимым, т.е. его можно использовать для анализа и
прогнозирования.
Уровень точности модели
характеризует степень отклонения в среднем фактических значений результативной переменной
Y от ее
значений, полученных по модели регрессии.
Точность модели оценим с помощью
средней ошибки аппроксимации:
Модель считается неточной, т.к. 
Таблица
6
|
у |
х1 |
yt |
et |
|
|
|
1440075 |
4 |
1276885 |
163190,1 |
163190,1 |
0,127803 |
|
5146 |
50798 |
40788,62 |
-35642,6 |
35642,62 |
0,873837 |
|
13612 |
18 |
32692,08 |
-19080,1 |
19080,08 |
0,58363 |
|
964 |
13 |
31294,64 |
-30330,6 |
30330,64 |
0,969196 |
|
19513178 |
63 |
16088906 |
3424272 |
-3424272 |
-0,21283 |
|
28973 |
367 |
121279,8 |
-92306,8 |
92306,81 |
0,761106 |
|
-780599 |
3 |
1026465 |
-1807064 |
1807064 |
1,760473 |
|
2598165 |
5 |
1528357 |
1069808 |
1069808 |
0,699973 |
|
628091 |
5 |
1379848 |
-751757 |
751757,1 |
0,544812 |
|
29204 |
705 |
207080,3 |
-177876 |
177876,3 |
0,858973 |
|
1945560 |
2 |
780374,6 |
1165185 |
1165185 |
1,49311 |
|
366170 |
624 |
186463,6 |
179706,4 |
179706,4 |
0,963761 |
|
-20493 |
46 |
39755,45 |
-60248,5 |
60248,45 |
1,515476 |
|
381558 |
582 |
175781,6 |
205776,4 |
205776,4 |
1,170637 |
|
1225908 |
3 |
907105 |
318803 |
318803 |
0,351451 |
|
3293989 |
5 |
1523335 |
1770654 |
1770654 |
1,162354 |
|
416616 |
299 |
103867,2 |
312748,8 |
312748,8 |
3,011043 |
|
-564258 |
801 |
231297,3 |
-795555 |
795555,3 |
3,439536 |
|
221194 |
257 |
93293,64 |
127900,4 |
127900,4 |
1,370944 |
|
701035 |
1 |
425432,4 |
275602,6 |
275602,6 |
0,647817 |
|
62200 |
528 |
162157,7 |
-99957,7 |
99957,75 |
0,616423 |
|
123440 |
167 |
70361,86 |
53078,14 |
53078,14 |
0,754359 |
|
55528 |
52 |
41104,41 |
14423,59 |
14423,59 |
0,350901 |
|
422070 |
188 |
75785,36 |
346284,6 |
346284,6 |
4,569281 |
|
-468 |
130 |
60982,88 |
-61450,9 |
61450,88 |
1,007674 |
|
225452 |
585 |
176400 |
49052,01 |
49052,01 |
0,278073 |
|
-61237 |
344 |
115318,9 |
-176556 |
176555,9 |
1,531023 |
|
-540 |
36 |
37194,87 |
-37734,9 |
37734,87 |
1,014518 |
|
40588 |
215 |
82498,17 |
-41910,2 |
41910,17 |
0,508013 |
|
53182 |
998 |
281457,7 |
-228276 |
228275,7 |
0,811048 |
|
-210 |
1 |
28325,61 |
-28535,6 |
28535,61 |
1,007414 |
|
63058 |
807 |
232924,5 |
-169866 |
169866,5 |
0,729277 |
|
1197196 |
1 |
425929,5 |
771266,5 |
771266,5 |
1,810785 |
|
221177 |
128 |
60451,32 |
160725,7 |
160725,7 |
2,658762 |
|
1548768 |
7 |
1987689 |
-438921 |
438921,4 |
0,22082 |
|
-33030 |
14 |
31552,04 |
-64582 |
64582,04 |
2,046842 |
|
34929 |
921 |
261900,4 |
-226971 |
226971,4 |
0,866633 |
|
115847 |
233 |
87126,86 |
28720,14 |
28720,14 |
0,329636 |
|
35198 |
361 |
119703,9 |
-84505,9 |
84505,91 |
0,705958 |
|
788567 |
458 |
144215,9 |
644351,1 |
644351,1 |
4,467962 |
|
309053 |
619 |
185141,3 |
123911,7 |
123911,7 |
0,669282 |
|
8552 |
119 |
58211,85 |
-49659,9 |
49659,85 |
0,853088 |
|
173079 |
93168,49 |
79910,51 |
79910,51 |
0,857699 |
|
|
1227017 |
4215454 |
1097986 |
129031,4 |
129031,4 |
0,117517 |
|
701728 |
324 |
110386,6 |
591341,4 |
591341,4 |
5,357003 |
|
17927 |
81 |
48699,09 |
-30772,1 |
30772,09 |
0,631882 |
|
2557698 |
35 |
8971546 |
-6413848 |
6413848 |
0,71491 |
|
0 |
76 |
47295,3 |
-47295,3 |
47295,3 |
1 |
|
5406 |
21 |
33257,91 |
-27851,9 |
27851,91 |
0,837452 |
|
40997 |
79 |
48183,77 |
-7186,77 |
7186,773 |
0,149153 |
|
41377260 |
104129376 |
41377260 |
3E-09 |
59,56649 |
|
|
827545,2 |
2082587,52 |
. Проверьте выполнение условия
гомоскедастичности
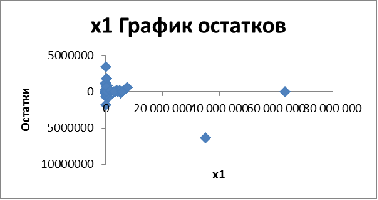
Рис. 4. Графики остатков по фактору
однофакторной модели
Из графиков, представленных на рис. 4.3, видно,
что дисперсия остатков более всего нарушена по отношению к фактору Х3.
Проверим наличие гомоскедастичности в остатках
однофакторной модели на основе теста Гольдфельда-Квандта.
. Упорядочим переменные Y и X1 по возрастанию
фактора Х3(в Excel для этого можно использовать команду Данные — Сортировка по
возрастанию Х3):
Данные, отсортированные по возрастанию Х3 (Рис.
5)
. Убираем из середины упорядоченной
совокупности C=1/4*50 = 12
значений. В результате получили две совокупности по ½
(50-12)
= 19 значений соответственно с малыми и большими значениями X3.
2. Для каждой совокупности выполним
регрессионный анализ (табл. 7-8).
Рис. 5
Таблица
7
Таблица
8
. Находим отношение полученных остаточных сумм
квадратов
R = 3,47E+12/8,92Е+13=
0,039
. Вывод о наличии гомоскедастичности остатков
делаем с помощью F- критерия
Фишера с уровнем значимости и двумя
одинаковыми степенями свободы
к = 18 (k=(n-C-2*p)/2,
где р — число коэффициентов в
уравнении регрессии).
Fтабл. = 2,21
Так как Fтабл<R,
то обнаруживается наличие гетероскедастичности в остатках модели по отношению к
фактору X3.
. Используя результаты регрессионного анализа,
ранжируйте компании по степени эффективности
Для ранжирования компаний по степени
эффективности, построим доверительные интервалы для результирующей переменной.
Доверительный интервал для отдельных значений
переменной можно определить рассчитав вначале ошибку моделирования:
Где Х — матрица факторов.
Можно применить упрощенную формулу одинаковую
для всех уровней:
Верхняя граница доверительного
интервала:
Нижняя граница доверительного
интервала:
Таблица
9
|
у |
х1 |
Предсказанное |
Остатки |
|
1440075 |
4 |
1276885 |
163190,1 |
|
5146 |
50798 |
40788,62 |
-35642,6 |
|
13612 |
18 |
32692,08 |
-19080,1 |
|
964 |
13 |
31294,64 |
-30330,6 |
|
19513178 |
63 |
16088906 |
3424272 |
|
28973 |
367 |
121279,8 |
-92306,8 |
|
-780599 |
3 |
1026465 |
-1807064 |
|
2598165 |
5 |
1528357 |
1069808 |
|
628091 |
5 |
1379848 |
-751757 |
|
29204 |
705 |
207080,3 |
-177876 |
|
1945560 |
2 |
780374,6 |
1165185 |
|
366170 |
624 |
186463,6 |
179706,4 |
|
-20493 |
46 |
39755,45 |
-60248,5 |
|
381558 |
582 |
175781,6 |
205776,4 |
|
1225908 |
3 |
907105 |
318803 |
|
3293989 |
5 |
1523335 |
1770654 |
|
416616 |
299 |
103867,2 |
312748,8 |
|
-564258 |
801 |
231297,3 |
-795555 |
|
221194 |
257 |
93293,64 |
127900,4 |
|
701035 |
1 |
425432,4 |
275602,6 |
|
62200 |
528 |
162157,7 |
-99957,7 |
|
123440 |
167 |
70361,86 |
53078,14 |
|
55528 |
52 |
41104,41 |
14423,59 |
|
422070 |
188 |
75785,36 |
346284,6 |
|
-468 |
130 |
60982,88 |
-61450,9 |
|
225452 |
585 |
176400 |
49052,01 |
|
-61237 |
344 |
115318,9 |
-176556 |
|
-540 |
36 |
37194,87 |
-37734,9 |
|
40588 |
215 |
82498,17 |
-41910,2 |
|
53182 |
998 |
281457,7 |
-228276 |
|
-210 |
1 |
28325,61 |
-28535,6 |
|
63058 |
807 |
232924,5 |
-169866 |
|
1197196 |
1 |
425929,5 |
771266,5 |
|
221177 |
128 |
60451,32 |
160725,7 |
|
1548768 |
7 |
1987689 |
-438921 |
|
-33030 |
14 |
31552,04 |
-64582 |
|
34929 |
921 |
261900,4 |
-226971 |
|
115847 |
233 |
87126,86 |
28720,14 |
|
35198 |
361 |
119703,9 |
-84505,9 |
|
788567 |
458 |
144215,9 |
644351,1 |
|
309053 |
619 |
185141,3 |
123911,7 |
|
8552 |
119 |
58211,85 |
-49659,9 |
|
173079 |
257 |
93168,49 |
79910,51 |
|
1227017 |
4215454 |
1097986 |
129031,4 |
|
701728 |
324 |
110386,6 |
591341,4 |
|
17927 |
81 |
48699,09 |
-30772,1 |
|
2557698 |
35 |
8971546 |
-6413848 |
|
0 |
76 |
47295,3 |
-47295,3 |
|
5406 |
21 |
33257,91 |
-27851,9 |
|
40997 |
79 |
48183,77 |
-7186,77 |
9. Осуществите прогнозирование
среднего значения показателя Y при уровне значимости = 0,1, если прогнозное значение
фактора Хj составит 80% от его максимального значения. Представьте на графике
фактические данные Y, результаты моделирования, прогнозные оценки и границы
доверительного интервала
1. Точечный прогноз фактора:
Xпрог = 0,8*52034182
= 41627345,6
. Точечный прогноз прибыли:
При значении долгосрочных обязательств41627345,6
тыс. руб. прибыль составит в среднем 11614177,2тыс.руб.
. Интервальный прогноз прибыли:
Найдем ошибку прогнозирования по формуле:
Которая зависит от стандартной ошибки Sе,
удаления Xпр от своего
среднего значения, количества наблюдений n,
заданного уровня вероятности попадания в интервал прогноза.
t(0,1;48) = 1,6772e
= 1414240,697
Xср = 2082587,52
Нижняя граница интервала
Yпр — U
= 11614177,2 — 5036306,495 = 6577870,695
Верхняя граница интервала
Yпр + U
= 11614177,2 + 5036306,495 = 16650483,68
Вывод: при значении долгосрочных обязательств
41627345,6 тыс. руб. прибыль будет колебаться в пределах от 6577870,695 тыс.
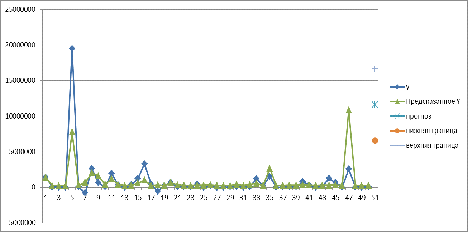
руб. до 16650483,68 тыс. руб. Графическое представление результатов
моделирования по парной регрессии отражено на рис. 5.
10. Составьте уравнения нелинейной регрессии
Используя MS Excel и VSTAT, подберите для данных
своего варианта наилучшую трендовую модель и выполните прогнозирование по
лучшей модели на два ближайших периода. Представьте в отчете соответствующие
листинги с комментариями.
· Щёлкните правой кнопкой мыши на ряде динамики
· Выберите команду Добавить линию
тренда из контекстного меню
· Выберите тип регрессии. При выборе
типа Полиноминальная введите значение степени в поле Степень
· В параметрах отметить:
— показывать уравнение на диаграмме
поместить на диаграмму величину достоверности
аппроксимации
· Щелкните Ок.
а) гиперболической;
б) степенной;
Степенная функция не построена (не
идентифицирована)
в) показательной
. Приведите графики построенных уравнений
регрессии
Графики приведены в 10 п.
. Для нелинейных моделей найдите коэффициенты
детерминации и средние относительные ошибки аппроксимации. Сравните модели по
этим характеристикам и сделайте вывод о лучшей модели
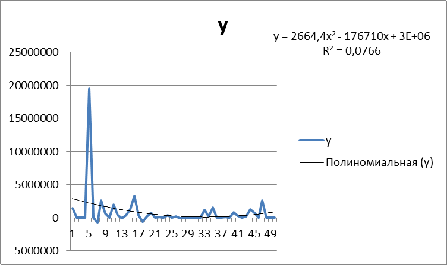
Таблица
10
Сравнение нелинейных моделей
|
Модель |
R^2 |
Еотн.ср. |
|
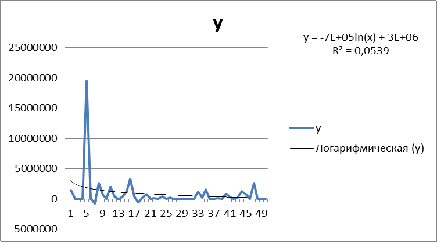
Показательная |
0,0539 |
0,45 |
|
Гиперболическая |
0,0766 |
7,855 |
Наилучшей трендовой моделью считается
гиперболическая, так как у нее большее значение коэффициента детерминации. Ее
то мы и возьмем в качестве лучшей для построения прогноза.
Консультация и поддержка студентов в учёбе
Главная » Бесплатные рефераты » Бесплатные рефераты по эконометрике »
![Контрольная работа по Эконометрике Решение в Excel [01.04.17]](https://studrb.ru/files/works_screen/3/37/96.png)
Тема: Контрольная работа по Эконометрике Решение в Excel
Раздел: Бесплатные рефераты по эконометрике
Тип: Контрольная работа | Размер: 77.45K | Скачано: 234 | Добавлен 01.04.17 в 17:07 | Рейтинг: 0 | Еще Контрольные работы
| Задание № 1 | ||||||
| На основании данных, приведенных в табл. 14 : | ||||||
| 1. Постройте диаграммы рассеяния, представляющие собой зависимости Y от каждого из факторов Х. Сделайте выводы о характере взаимосвязи переменных. | ||||||
| 2. Постройте матрицу коэффициентов парной корреляции. | ||||||
| Парная регрессия | ||||||
| 3. Рассчитайте параметры линейной парной регрессии для наиболее подходящего фактора Хj. | ||||||
| (Выбор фактора можно сделать на основе анализа матрицы коэффициентов парной корреляции – выбираем тот фактор, который наиболее тесно связан с зависимой переменной). | ||||||
| 4. Оцените качество построенной модели с помощью коэффициента детерминации, F-критерия Фишера. | ||||||
| 5. Проверьте выполнение условия гомоскедастичности. | ||||||
| 6. Используя результаты регрессионного анализа ранжируйте компании по степени эффективности. | ||||||
| 7. Осуществите прогнозирование среднего значения показателя Y при уровне значимости α = 0,1, если прогнозное значение фактора Хj составит 80% от его максимального значения. | ||||||
| Представьте на графике фактические данные Y, результаты моделирования, прогнозные оценки и границы доверительного интервала. | ||||||
| 8. Для 12 предприятий, имеющих наибольшую прибыль, составьте уравнения нелинейной регрессии: | ||||||
| а) гиперболической; | ||||||
| б) степенной; | ||||||
| в) показательной. | ||||||
| 9. Приведите графики построенных уравнений регрессии. | ||||||
| 10. Множественная регрессия | ||||||
| 1. Осуществите двумя способами выбор факторных признаков для по- строения регрессионной модели: | ||||||
| а) на основе визуального анализа матрицы коэффициентов парной корреляции; | ||||||
| б) с помощью пошагового отбора методом исключения. | ||||||
| 2. Постройте уравнение множественной регрессии в линейной форме с выбранными факторами. Дайте экономическую интерпретацию коэффициентов модели регрессии. | ||||||
| 3. Дайте сравнительную оценку силы связи факторов с результатом с помощью коэффициентов эластичности, β- и Δ-коэффициентов. | ||||||
| Таблица «Данные к задаче 2» | ||||||
| Таблица 1. Добыча сырой нефти и природного газа, предоставление услуг в этих областях (данные за 2009 г.) | ||||||
| Добыча сырой нефти и природного газа; предоставление услуг в этих областях | № п.п. | Прибыль (убыток) | Долгосрочные обязательства | Краткосрочные обязательства | Дебиторская задолженность (краткосрочная) | Основные средства |
| Y | X1 | X2 | X5 | X4 | ||
| Акционерная нефтяная Компания Башнефть, Открытое акционерное общество | 5 | 19513178,0 | 52034182,0 | 2411352,0 | 23780450,0 | 47002385,0 |
| АЛРОСА -Газ, Открытое акционерное общество | 6 | 28973,0 | 602229,0 | 74839,0 | 204181,0 | 1545052,0 |
| Арктическая газовая компания, открытое акционерное общество | 7 | -780599,0 | 311268,0 | 15737048,0 | 1456438,0 | 740437,0 |
| Барьеганнефтегаз, Открытое акционерное общество | 8 | 2598165,0 | 464651,0 | 4381403,0 | 5566412,0 | 11925177,0 |
| Белкамнефть, Открытое акционерное общество | 9 | 628091,0 | 214411,0 | 3728587,0 | 4285041,0 | 2580485,0 |
| Белорусское управление по повышению нефтеотдачи пластов и капитальному ремонту скважин, открытое акционерное общество | 10 | 29204,0 | 12039,0 | 738811,0 | 624393,0 | 269908,0 |
| Битран, Открытое акционерное общество | 11 | 1945560,0 | 9670,0 | 716648,0 | 2918345,0 | 229855,0 |
| Богородскнефть, Открытое акционерное общество | 12 | 366170,0 | 287992,0 | 239076,0 | 484537,0 | 349643,0 |
| Братскэкогаз, Открытое акционерное общество | 13 | -20493,0 | 1105293,0 | 8855,0 | 9865,0 | 934881,0 |
| Булгарнефть, Открытое акционерное общество | 14 | 381558,0 | 27265,0 | 265569,0 | 196045,0 | 697664,0 |
| Варьеганнефть, Открытое акционерное общество | 15 | 1225908,0 | 431231,0 | 1525379,0 | 1095263,0 | 2231651,0 |
| Верхнечонскнефтегаз, Открытое акционерное общество | 16 | 3293989,0 | 37315847,0 | 8556455,0 | 2477424,0 | 23170344,0 |
| Восточная транснациональная компания, Открытое акционерное общество | 17 | 416616,0 | 2122138,0 | 258120,0 | 48174,0 | 3509537,0 |
| Восточно-Сибирская нефтегазовая компания, Открытое акционерное общество | 18 | -564258,0 | 1395080,0 | 7958766,0 | 286058,0 | 1290245,0 |
| Геолого-разведочный исследовательский центр, Открытое акционерное общество | 19 | 221194,0 | 13429,0 | 105123,0 | 72854,0 | 607249,0 |
| ГРОЗНЕФТЕГАЗ, ОТКРЫТОЕ АКЦИОНЕРНОЕ ОБЩЕСТВО | 20 | 701035,0 | 75554,0 | 497028,0 | 1304084,0 | 4616250,0 |
| Губкинский газоперерабатывающий комплекс, открытое акционерное общество | 21 | 62200,0 | 22195,0 | 1659245,0 | 294575,0 | 991114,0 |
| ДАГНЕФТЕГАЗ, ОТКРЫТОЕ АКЦИОНЕРНОЕ ОБЩЕСТВО | 22 | 123440,0 | 12350,0 | 84026,0 | 44889,0 | 438262,0 |
| Елабуганефть, Открытое акционерное общество | 23 | 55528,0 | 14686,0 | 137348,0 | 24275,0 | 75442,0 |
| Иделойл, Открытое акционерное общество | 24 | 422070,0 | 52443,0 | 662299,0 | 140535,0 | 1269731,0 |
| Избербашнефть, Открытое акционерное общество | 25 | -468,0 | 239255,0 | 29880,0 | 114444,0 | 10870,0 |
| ИНВЕСТИЦИОННАЯ НЕФТЯНАЯ КОМПАНИЯ, ОТКРЫТОЕ АКЦИОНЕРНОЕ ОБЩЕСТВО | 26 | 225452,0 | 1292,0 | 87112,0 | 272147,0 | 227132,0 |
| Инга, Открытое акционерное общество | 27 | -61237,0 | 924951,0 | 299733,0 | 76561,0 | 110970,0 |
| КАББАЛКНЕФТЕТОППРОМ, ОТКРЫТОЕ АКЦИОНЕРНОЕ ОБЩЕСТВО | 28 | -540,0 | 0,0 | 46139,0 | 25017,0 | 21278,0 |
| Калининграднефть, Открытое акционерное общество | 29 | 40588,0 | 1638,0 | 22683,0 | 18072,0 | 139209,0 |
| КАМЧАТГАЗПРОМ, ОТКРЫТОЕ АКЦИОНЕРНОЕ ОБЩЕСТВО | 30 | 53182,0 | 54758,0 | 1909328,0 | 496994,0 | 113113,0 |
| КИРОВСКОЕ НЕФТЕГАЗОДОБЫВАЮЩЕЕ УПРАВЛЕНИЕ, ОТКРЫТОЕ АКЦИОНЕРНОЕ ОБЩЕСТВО | 31 | -210,0 | 8,0 | 16191,0 | 602,0 | 12685,0 |
| Когалымнефтепрогресс, Открытое акционерное общество | 32 | 63058,0 | 235731,0 | 563481,0 | 474612,0 | 873886,0 |
| Комнедра, Открытое акционерное общество | 33 | 1197196,0 | 2232742,0 | 1083829,0 | 1040387,0 | 2307478,0 |
| Кондурчанефть, Открытое акционерное общество | 34 | 221177,0 | 4682,0 | 40664,0 | 55155,0 | 331954,0 |
| Корпорация югранефть, открытое акционерное общество | 35 | 1548768,0 | 84262,0 | 413994,0 | 7613662,0 | 1138707,0 |
| Краснодарское опытно- экспериментальное управление по повышению нефтеотдачи пластов и капитальному ремонту скважин, открытое акционерное общество | 36 | -33030,0 | 106,0 | 52575,0 | 5038,0 | 16705,0 |
| Ленинградсланец, открытое акционерное общество | 37 | -34929,0 | 103567,0 | 1769300,0 | 61353,0 | 393717,0 |
| Меллянефть, Открытое акционерное общество | 38 | 115847,0 | 275386,0 | 432312,0 | 122062,0 | 517290,0 |
| МНКТ, Общество с ограниченной ответственностью | 39 | 35198,0 | 20624,0 | 169155,0 | 168314,0 | 484228,0 |
| Мохтикнефть, Открытое акционерное общество | 40 | 788567,0 | 33879,0 | 647914,0 | 317153,0 | 402613,0 |
| НАУЧНО-ПРОИЗВОДСТВЕННОЕ ОБЪЕДИНЕНИЕ СПЕЦЭЛЕКТРОМЕХАНИКА, ОТКРЫТОЕ АКЦИОНЕРНОЕ ОБЩЕСТВО | 41 | 309053,0 | 99670,0 | 211624,0 | 212882,0 | 18776,0 |
| НАУЧНО-ПРОИЗВОДСТВЕННОЕ ПРЕДПРИЯТИЕ БУРСЕРВИС, ОТКРЫТОЕ АКЦИОНЕРНОЕ ОБЩЕСТВО | 42 | 8552,0 | 257,0 | 99815,0 | 63550,0 | 12381,0 |
| НГДУ Пензанефть, Открытое акционерное общество | 43 | 173079,0 | 6120,0 | 114223,0 | 147549,0 | 176126,0 |
| НЕГУСНЕФТЬ, ОТКРЫТОЕ АКЦИОНЕРНОЕ ОБЩЕСТВО | 44 | 1227017,0 | 33757,0 | 1930517,0 | 171162,0 | 2063285,0 |
| НЕНЕЦКАЯ НЕФТЯНАЯ КОМПАНИЯ, ОТКРЫТОЕ АКЦИОНЕРНОЕ ОБЩЕСТВО | 45 | 701728,0 | 381050,0 | 335238,0 | 237083,0 | 59353,0 |
| НЕФТЕБУРСЕРВИС, ОТКРЫТОЕ АКЦИОНЕРНОЕ ОБЩЕСТВО | 46 | 17927,0 | 53260,0 | 101834,0 | 73343,0 | 84818,0 |
| Нефтегазовая компания Славнефть, Открытое акционерное общество | 47 | 2557698,0 | 4537040,0 | 21786237,0 | 33477251,0 | 3841845,0 |
| Нефтеразведка, Открытое акционерное общество | 48 | 0,0 | 194091,0 | 64889,0 | 15161,0 | 33112,0 |
| Нефть, Открытое акционерное общество | 49 | 5406,0 | 1185,0 | 27941,0 | 7540,0 | 38560,0 |
| Нефтьинвест, Открытое акционерное общество | 50 | 40997,0 | 101706,0 | 39653,0 | 58762,0 | 178604,0 |
| НЕФТЯНАЯ АКЦИОНЕРНАЯ КОМПАНИЯ АКИ-ОТЫР, ОТКРЫТОЕ АКЦИОНЕРНОЕ ОБЩЕСТВО | 51 | 1580624,0 | 9285230,0 | 1476613,0 | 259519,0 | 6546853,0 |
| Нефтяная компания Магма, Открытое акционерное общество | 52 | 9990896,0 | 1645470,0 | 5066776,0 | 7271400,0 | 2329554,0 |
| НЕФТЯНАЯ КОМПАНИЯ МАНГАЗЕЯ, ОТКРЫТОЕ АКЦИОНЕРНОЕ ОБЩЕСТВО | 53 | 6649,0 | 82229,0 | 1486511,0 | 444251,0 | 78526,0 |
| Нефтяная компания Нефтиса, Открытое акционерное общество | 54 | 22868,0 | 3,0 | 76455,0 | 28536,0 | 9067,0 |
| Задание № 2 | |||||||||||||
| В течение девяти последовательных недель фиксировался спрос Y(t) (млн. р.) на кредитные ресурсы финансовой компании. | |||||||||||||
| Временной ряд Y(t) этого показателя (повариантно) приведен ниже в таблице. | |||||||||||||
| Номер наблюдения (t = 1,2,…,9) | |||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||||
| 45 | 43 | 40 | 36 | 38 | 34 | 31 | 28 | 25 | |||||
| Требуется: | |||||||||||||
| 1) Проверить наличие аномальных наблюдений. | |||||||||||||
| 2) Построить линейную модель `U (t) = a0 + a1 t, параметры которой оценить МНК`U (t) — расчетные, смоделированные значения временного ряда): | |||||||||||||
| a) использованием Поиска решений; | |||||||||||||
| b) использованием матричных функций; | |||||||||||||
| c) использованием Мастера диаграмм. | |||||||||||||
| 3) Оценить адекватность модели, используя свойства независимости остаточной компоненты, случайности и соответствия нормальному закону распределения | |||||||||||||
| (при использовании R/S-критерия взять табулированные границы 2,7— 3,7). | |||||||||||||
| 4) Оценить точность модели с помощью средней относительной ошибки аппроксимации. | |||||||||||||
| 5) Осуществить прогноз спроса на следующие две недели (доверительный интервал прогноза рассчитать при доверительной вероятности р = 80%). | |||||||||||||
| 6) Построить адаптивную модель Брауна `U (t) = a0 + a1 k с параметром сглаживания α= 0,4 и α= 0,7; выбрать лучшее значение параметра сглаживания α. | |||||||||||||
| 7) Фактические значения показателя, результаты моделирования по двум моделям `(U (t) = a0 + a1 t и лучшей модели Брауна) и прогнозирования представить графически. |
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы
Бесплатная оценка
0
01.04.17 в 17:07
Автор:Ilmira
Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).
Чтобы скачать бесплатно Контрольные работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.
Важно! Все представленные Контрольные работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.
Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.
Добавить работу
Если Контрольная работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.
Добавление отзыва к работе
Добавить отзыв могут только зарегистрированные пользователи.
Консультация и поддержка студентов в учёбе
Гомоскедастичность (Homoscedasticity)
Гомоскедастичность – допущение линейной регрессии об «одинаковости» Дисперсии (Variance). Иными словами, разность между реальным Ypred и предсказанным Yactual значениями, скажем, Линейной регрессии (Linear Regresion) остается в определенном известном диапазоне, что позволяет в принципе использовать такую Модель (Model). В случае такого единообразия ошибок Наблюдения (Observation) с большими значениями будут иметь то же влияние на предсказывающий Алгоритм (Algorithm), что и наблюдения с меньшими значениями:
Линейная регрессия базируется на предположении, что для всех случаев ошибки будут одинаковыми и с очень малой дисперсией.
Пример. У нас есть две переменные – высота дерева навскидку и реальный его рост. Естественно, по мере увеличения оценочной высоты реальные тоже растут. Итак, мы подбираем модель линейной регрессии и видим, что ошибки имеют одинаковую дисперсию:
Прогнозы почти совпадают с линейной регрессией и имеют одинаковую известную дисперсию повсюду. Кроме того, если мы нанесем эти остатки на ось X, мы увидим их вдоль прямой линии, параллельной оси X. Это явный признак гомоскедастичности.
Когда это условие нарушается, в модели присутствует Гетероскедастичность (Heteroscedasticity). Предположим, что для деревьев с меньшей приблизительной высотой разность между прогнозируемым и реальным значением меньше, чем для высоких представителей флоры. По мере увеличения высоты дисперсия в прогнозах увеличивается, что приводит к увеличению значения ошибки или Остатка (Residual). Когда мы снова построим график остатков, то увидим типичную коническую кривую, которая четко указывает на наличие гетероскедастичности в модели:
Гетероскедастичность – это систематическое увеличение или уменьшение дисперсии остатков в диапазоне независимых переменных. Это проблема, потому нарушается базовое предположение о линейной регрессии: все ошибки должны иметь одинаковую дисперсию.
Как узнать, присутствует ли гетероскедастичность?
Проще говоря, самый простой способ узнать, присутствует ли гетероскедастичность, – построить график остатков. Если вы видите какую-либо закономерность, значит, есть гетероскедастичность. Обычно значения увеличиваются, образуя конусообразную кривую.
Причины гетероскедастичности
- Есть большая разница в переменной. Другими словами, когда наименьшее и наибольшее значения переменной слишком экстремальны. Это также могут быть Выбросы (Outlier).
- Мы выбираем неправильную модель. Если вы подгоните модель линейной регрессии к нелинейным данным, это приведет к гетероскедастичности.
- Когда масштаб значений в переменной некорректен (например, стоит рассматривать данные по сезонам, а не по дням).
- Когда для регрессии используется неправильное преобразование данных.
- Когда в данных присутствует Скошенность (Skewness).
Чистая и нечистая гетероскедастичности
Когда мы подбираем правильную модель (линейную или нелинейную) и все же есть видимый образец в остатках, это называется чистой гетероскедастичностью.
Однако, если мы подбираем неправильную модель, а затем наблюдаем закономерность в остатках, то это случай нечистой гетероскедастичности. В зависимости от типа гетероскедастичности необходимо принять меры для ее преодоления. Это зависит и от сферы, в которой мы работаем.
Эффекты гетероскедастичности в Машинном обучении
Как мы обсуждали ранее, модель линейной регрессии делает предположение о наличии гомоскедастичности в данных. Если это предположение неверно, мы не сможем доверять полученным результатам.
Наличие гетероскедастичности делает коэффициенты менее точными, и, следовательно, правильные находятся дальше от значения Генеральной совокупности (Population).
Как лечить гетероскедастичность?
Если мы обнаружили гетероскедастичность, есть несколько способов справиться с ней. Во-первых, давайте рассмотрим пример, в котором у нас есть две переменные: население города и количество заражений COVID-19.
В этом примере будет огромная разница в количестве заражений в крупных мегаполисах по сравнению с небольшими городами. Переменная «Количество инфекций» будет Целевой переменной (Target Variable), а «Население города» – Предиктором (Predictor Variable). Мы знаем, что в модели присутствует гетероскедастичность, и ее необходимо исправить.
В нашем случае, источник проблемы – это переменная с большой дисперсией (Население). Есть несколько способов справиться с подобным неоднообразием остатков, мы же рассмотрим три таких метода.
Управление переменными
Мы можем внести некоторые изменения в имеющиеся переменные, чтобы уменьшить влияние этой большой дисперсии на прогнозы модели. Один из способов сделать это – осуществить Нормализацию (Normalization), то есть привести значения Признака (Feature) к диапазону от 0 до 1. Это заставит признаки передавать немного другую информацию. От проблемы и данных будет зависеть, можно ли реализовать такой подход.
Этот метод требует минимальных модификаций и часто помогает решить проблему, а в некоторых случаях даже повысить производительность модели.
В нашем случае, мы изменим параметр «Количество инфекций» на «Скорость заражения». Это поможет уменьшить дисперсию, поскольку совершенно очевидно, что число инфекций в городах с большой численностью населения будет большим.
Взвешенная регрессия
Взвешенная регрессия – это модификация нормальной регрессии, при которой точкам данных присваиваются определенные Веса (Weights) в соответствии с их дисперсией. Те, у которых есть бо́льшая дисперсия, получают небольшой вес, а те, у которых меньшая дисперсия, получают бо́льший вес.
Таким образом, когда веса возведены в квадрат, это позволяет снизить влияние остатков с большой дисперсией.
Когда используются правильные веса, гетероскедастичность заменяется гомоскедастичностью. Но как найти правильный вес? Один из быстрых способов – использовать инверсию этой переменной в качестве веса (население города превратится в дробь 1/n, где n – число жителей).
Трансформация
Преобразование данных – последнее средство, поскольку при этом вы теряете интерпретируемость функции. Это означает, что вы больше не сможете легко объяснить, что показывает признак. Один из способов – взятие логарифма. Воспринять новые значения высоты дерева (например, 16 метров превратятся в ≈2.772) будет сложнее.
Контрольная работа: Контрольная работа по эконометрике вариант №8
Тема: Контрольная работа по эконометрике вариант №8
Тип: Контрольная работа | Размер: 29.98K | Скачано: 176 | Добавлен 07.04.16 в 21:06 | Рейтинг: 0 | Еще Контрольные работы
Вуз: Финансовый университет
Год и город: Владимир 2015
Вариант 8
По 14 страховым компаниям имеются данные, характеризующие зависимость объема чистой годовой прибыли от годовых объемов собственных средств, страховых резервов, страховых премий и страховых выплат, тыс. руб.:
1. Постройте линейную регрессионную модель объема чистой годовой прибыли страховой компании, не содержащую коллинеарных факторов. Оцените параметры модели.
2. Являются ли уравнение регрессии и его коэффициенты статистически значимыми?
3. Имеют ли остатки регрессии одинаковую дисперсию?
4. Приемлема ли точность регрессионной модели?
5. Дайте экономическую интерпретацию коэффициентов уравнения регрессии.
6. Изменение какого фактора сильнее всего влияет на изменение объема годовой прибыли?
7. Используя результаты регрессионного анализа, ранжируйте компании по степени эффективности деятельности.
Чтобы полностью ознакомиться с контрольной, скачайте файл!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы
Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).
Чтобы скачать бесплатно Контрольные работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.
Важно! Все представленные Контрольные работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.
Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.
Если Контрольная работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.
Добавление отзыва к работе
Добавить отзыв могут только зарегистрированные пользователи.
Ответы на тесты по эконометрике
Q=………..min соответствует методу наименьших квадратов
Автокорреляция — это корреляционная зависимость уровней ряда от предыдущих значений.
Автокорреляция имеется когда каждое следующее значение остатков
Аддитивная модель временного ряда имеет вид: Y=T+S+E
Атрибутивная переменная может употребляться, когда: независимая переменная качественна;
В каких пределах изменяется коэффициент детерминанта: от 0 до 1.
В каком случае модель считается адекватной Fрасч>Fтабл
В каком случае рекомендуется применять для моделирования показателей с увелич. ростом параболу если относительная величина…неограниченно
В результате автокорреляции имеем неэффективные оценки параметров
В хорошо подобранной модели остатки должны иметь нормальный закон
В эконометрическом анализе Xj рассматриваются как случайные величины
Величина доверительного интервала позволяет установить предположение о том, что: интервал содержит оценку параметра неизвестного.
Величина рассчитанная по формуле r=…является оценкой парного коэф. Корреляции
Внутренне нелинейная регрессия — это истинно нелинейная регрессия, которая не может быть приведена к линейной регрессии преобразованием переменных и введением новых переменных.
Временной ряд — это последовательность значений признака (результативного переменного), принимаемых в течение последовательных моментов времени или периодов.
Выберете авторегрессионную модель Уt=a+b0x1+Ɣyt-1+ƹt
Выберете модель с лагами Уt= a+b0x1…….(самая длинная формула)
Выборочное значение Rxy не > 1, |R|
Выборочный коэффициент корреляции r по абсолютной величине не превосходит единицы
Гетероскедастичность — нарушение постоянства дисперсии для всех наблюдений.
Гетероскедастичность присутствует когда: дисперсия случайных остатков не постоянна
Гетероскидастичность – это когда дисперсия остатков различна
Гипотеза об отсутствии автокорреляции остатков доказана, если Dтабл2…
Гомоскедастичность — постоянство дисперсии для всех наблюдений, или одинаковость дисперсии каждого отклонения (остатка) для всех значений факторных переменных.
Гомоскидастичность – это когда дисперсия остатков постоянна и одинакова для всех … наблюдений.
Дисперсия — показатель вариации.
Для определения параметров неиденцифицированной модели применяется.: не один из сущ. методов применить нельзя
Для определения параметров сверх иденцифицированной модели примен.: применяется. 2-х шаговый МНК
Для определения параметров структурную форму модели необходимо преобразовать в приведенную форму модели
Для определения параметров точно идентифицируемой модели: применяется косвенный МНК;
Для оценки … изменения y от x вводится: коэффициент эластичности:
Для парной регрессии ơ²b равно ….(xi-x¯)²)
Для проверки значимости отдельных параметров регрессии используется: t-тест.
Для регрессии y=a+bx из n наблюдений интервал доверия (1-а)% для коэф. b составит b±t…….·ơb
Для регрессии из n наблюдений и m независимых переменных существует такая связь между R² и F..=[(n-m-1)/m]( R²/(1- R²)]
Доверительная вероятность – это вероятность того, что истинное значение результативного показателя попадёт в расчётный прогнозный интервал.
Допустим что для описания одного экономического процесса пригодны 2 модели. Обе адекватны по f критерию фишера. какой предоставить преимущество, у той у кот.: большее значения F критерия
Допустим, что зависимость расходов от дохода описывается функцией y=a+bx среднее значение у=2…равняется 9
Если Rxy положителен, то с ростом x увеличивается y.
Если в уравнении регрессии имеется несущественная переменная, то она обнаруживает себя по низкому значению T статистки
Если качественный фактор имеет 3 градации, то необходимое число фиктивных переменных 2
Если коэффициент корреляции положителен, то в линейной модели с ростом х увеличивается у
Если мы заинтересованы в использовании атрибутивных переменных для отображения эффекта разных месяцев мы должны использовать 11 атрибутивных методов
Если регрессионная модель имеет показательную зависимость, то метод МНК применим после приведения к линейному виду.
Зависимость между коэффициентом множественной детерминации (D) и корреляции (R) описывается следующим методом R=√D
Значимость уравнения регрессии — действительное наличие исследуемой зависимости, а не просто случайное совпадение факторов, имитирующее зависимость, которая фактически не существует.
Значимость уравнения регрессии в целом оценивают: -F-критерий Фишера
Значимость частных и парных коэф. корреляции поверен. с помощью: -t-критерия Стьюдента
Интеркорреляция и связанная с ней мультиколлинеарность — это приближающаяся к полной линейной зависимости тесная связь между факторами.
Какая статистическая характеристика выражается формулой R²=…коэффициент детерминации
Какая статистическая хар-ка выражена формулой : rxy=Ca(x;y) разделить на корень Var(x)*Var(y): коэффициент. корреляции
Какая функция используется при моделировании моделей с постоянным ростом степенная
Какие точки исключаются из временного ряда процедурой сглаживания и в начале, и в конце.
Какое из уравнений регрессии является степенным y=a˳aͯ¹a
Классический метод к оцениванию параметров регрессии основан на: – метод наименьших квадратов (МНК)
Количество степеней свободы для t статистики при проверки значимости параметров регрессии из 35 наблюдений и 3 независимых переменных 31;
Количество степеней свободы знаменателя F-статистики в регрессии из 50 наблюдений и 4 независимых переменных: 45
Компоненты вектора Ei имеют нормальный закон
Корреляция — стохастическая зависимость, являющаяся обобщением строго детерминированной функциональной зависимости посредством включения вероятностной (случайной) компоненты.
Коэффициент автокорреляции: характеризует тесноту линейной связи текущего и предстоящего уровней ряда
Коэффициент детерминации — показатель тесноты стохастической связи в общем случае нелинейной регрессии
Коэффициент детерминации – это величина, которая характеризует связь между зависимыми и независимыми переменными.
Коэффициент детерминации – это квадрат множественного коэффициента корреляции
Коэффициент детерминации – это: величина, которая характеризует связь между независимой и зависимой (зависящей) переменными;
Коэффициент детерминации R показывает долю вариаций зависимой переменной y, объяснимую влиянием факторов, включаемых в модель.
Коэффициент детерминации изменяется в пределах: – от 0 до 1
Коэффициент доверия — это коэффициент, который связывает линейной зависимостью предельную и среднюю ошибки, выясняет смысл предельной ошибки, характеризующей точность оценки, и является аргументом распределения (чаще всего, интеграла вероятностей). Именно эта вероятность и есть степень надежности оценки.
Коэффициент доверия (нормированное отклонение) — результат деления отклонения от среднего на стандартное отклонение, содержательно характеризует степень надежности (уверенности) полученной оценки.
Коэффициент корелляции Rxy используется для определения полноты связи X и Y.
Коэффициент корелляции меняется в пределах : от -1 до 1
Коэффициент корелляции равный 0 означает, что: –отсутствует линейная связь.
Коэффициент корелляции равный 1 означает, что: -существует функциональная зависимость.
Коэффициент корреляции используется для: определения тесноты связи между случайными величинами X и Y;
Коэффициент корреляции рассчитывается для измерения степени линейной взаимосвязи между двумя случайными переменными.
Коэффициент линейной корреляции — показатель тесноты стохастической связи между фактором и результатом в случае линейной регрессии.
Коэффициент регрессии — коэффициент при факторной переменной в модели линейной регрессии.
Коэффициент регрессии b показывает: на сколько единиц увеличивается y, если x увеличивается на 1.
Коэффициент регрессии изменяется в пределах: применяется любое значение ; от 0 до 1; от -1 до 1;
Коэффициент эластичности измеряется в: неизмеримая величина.
Критерий Дарвина-Чотсона применяется для: – отбора факторов в модель; или – определения автокорреляции в остатках
Критерий Стьюдента — проверка значимости отдельных коэффициентов регрессии и значимости коэффициента корреляции.
Критерий Фишера показывает статистическую значимость модели в целом на основе совокупной достоверности всех ее коэффициентов;
Лаговые переменные : – это переменные, относящиеся к предыдущим моментам времени; или -это значения зависим. перемен. за предшествующий период времени.
Лаговые переменные это значение зависимых переменных за предшествующий период времени
Модель в целом статистически значима, если Fрасч > Fтабл.
Модель идентифицирована, если: – число параметров структурной модели равно числу параметров приведён. формы модели.
Модель неидентифицирована, если: – число приведён. коэф . больше числа структурных коэф.
Модель сверхидентифицирована, если: число приведён. коэф. меньше числа структурных коэф
Мультиколлениарность возникает, когда: ошибочное включение в уравнение 2х или более линейно зависимых переменных; 2. две или более объясняющие переменные, в нормальной ситуации слабо коррелированные, становятся в конкретных условиях выборки сильно коррелированными; . в модель включается переменная, сильно коррелирующая с зависимой переменной.
Мультипликативная модель временного ряда имеет вид: – Y=T*S*E
Мультипликативная модель временного ряда строится, если: амплитуда сезонных колебаний возрастает или уменьшается
На основе поквартальных данных…значения 7-1 квартал, 9-2квартал и 11-3квартал …-5
Неправильный выбор функциональной формы или объясняющих переменных называется ошибками спецификации
Несмещённость оценки параметра регрессии, полученной по МНК, означает: – что она характеризуется наименьшей дисперсией.
Одной из проблем которая может возникнуть в многофакторной регрессии и никогда не бывает в парной регрессии, является корреляция между независимыми переменными
От чего зависит количество точек, исключаемых из временного ряда в результате сглаживания: от применяемого метода сглаживания.
Отметьте основные виды ошибок спецификации: отбрасывание значимой переменной; добавление незначимой переменной;
Оценки коэффициентов парной регрессии является несмещённым, если: математические ожидания остатков =0.
Оценки параметров парной линейной регрессии находятся по формуле b= Cov(x;y)/Var(x);a=y¯ bx¯
Оценки параметров регрессии являются несмещенными, если Математическое ожидание остатков равно 0
Оценки параметров регрессии являются состоятельными, если: -увеличивается точность оценки при n, т. е. при увеличении n вероятность оценки от истинного значения параметра стремится к 0.
Оценки парной регрессии явл. эффективными, если: оценка обладают наименьшей дисперсией по сравнению с другими оценками
При наличии гетероскедастичности следует применять: – обобщённый МНК
При проверке значимости одновременно всех параметров используется: -F-тест.
При проверке значимости одновременно всех параметров регрессии используется: F-тест.
Применим ли метод наименьших квадратов для расчетов параметров показательной зависимости применим после ее приведения
Применим ли метод наименьших квадратов(МНК) для расчёта параметров нелинейных моделей? применим после её специального приведения к линейному виду
С помощью какого критерия оценивается значимость коэффициента регрессии T стьюдента
С увеличением числа объясняющих переменных скоррестированный коэффициент детерминации: – увеличивается.
Связь между индексом множественной детерминации R² и скорректированным индексом множественной детерминации Ȓ² есть
Скорректиров. коэф. детерминации: – больше обычного коэф. детерминации
Стандартизованный коэффициент уравнения регрессии Ƀk показывает на сколько % изменится результирующий показатель у при изменении хi на 1%при неизмененном среднем уровне других факторов
Стандартный коэффициент уравнения регрессии: показывает на сколько 1 изменится y при изменении фактора xk на 1 при сохранении др.
Суть коэф. детерминации r 2 xy состоит в следующем: – характеризует долю дисперсии результативного признака y объясняем. регресс., в общей дисперсии результативного признака.
Табличное значение критерия Стьюдента зависит от уровня доверительной вероятности и от числа включённых факторов и от длины исходного ряда.(от принятого уровня значимости и от числа степеней свободы ( n – m -1))
Табличные значения Фишера (F) зависят от доверительной вероятности и от числа включённых факторов и от длины исходного ряда (от доверительной вероятности p и числа степеней свободы дисперсий f1 и f2)..
Уравнение в котором H число эндогенных переменных, D число отсутствующих экзогенных переменных, идентифицируемо если D+1=H
Уравнение в котором H число эндогенных переменных, D число отсутствующих экзогенных переменных, НЕидентифицируемо если D+1 H
Уравнение идентифицировано, если: – D+1=H
Уравнение неидентифицировано, если: – D+1 H
Фиктивные переменные – это: атрибутивные признаки (например, как профессия, пол, образование), которым придали цифровые метки;
Формула t= rxy….используется для проверки существенности коэффициента корреляции
Частный F-критерий: – оценивает значимость уравнения регрессии в целом
Число степеней свободы для факторной суммы квадратов в линейной модели множественной регрессии равно: m;
Что показывает коэффициент наклона – на сколько единиц изменится у, если х изменился на единицу,
Что показывает коэффициент. абсолютного роста на сколько единиц изменится у, если х изменился на единицу
Экзогенная переменная – это независимая переменная или фактор-Х.
Экзогенные переменные — это переменные, которые определяются вне системы и являются независимыми
Экзогенные переменные – это предопределенные переменные, влияющие на зависимые переменные (Эндогенные переменные), но не зависящие от них, обозначаются через х
Эластичность измеряется единица измерения фактора…показателя
Эластичность показывает на сколько % изменится редуктивный показатель y при изменении на 1% фактора xk .
Эндогенные переменные – это: зависимые переменные, число которых равно числу уравнений в системе и которые обозначаются через у
Определения
T-отношение (t-критерий) — отношение оценки коэффициента, полученной с помощью МНК, к величине стандартной ошибки оцениваемой величины.
Аддитивная модель временного ряда – это модель, в которой временной ряд представлен как сумма перечисленных компонент.
Критерий Фишера — способ статистической проверки значимости уравнения регрессии, при котором расчетное (фактическое) значение F-отношения сравнивается с его критическим (теоретическим) значением.
Линейная регрессия — это связь (регрессия), которая представлена уравнением прямой линии и выражает простейшую линейную зависимость.
Метод инструментальных переменных — это разновидность МНК. Используется для оценки параметров моделей, описываемых несколькими уравнениями. Главное свойство — частичная замена непригодной объясняющей переменной на такую переменную, которая некоррелированна со случайным членом. Эта замещающая переменная называется инструментальной и приводит к получению состоятельных оценок параметров.
Метод наименьших квадратов (МНК) — способ приближенного нахождения (оценивания) неизвестных коэффициентов (параметров) регрессии. Этот метод основан на требовании минимизации суммы квадратов отклонений значений результата, рассчитанных по уравнению регрессии, и истинных (наблюденных) значений результата.
Множественная линейная регрессия — это множественная регрессия, представляющая линейную связь по каждому фактору.
Множественная регрессия — регрессия с двумя и более факторными переменными.
Модель идентифицируемая — модель, в которой все структурные коэффициенты однозначно определяются по коэффициентам приведенной формы модели.
Модель рекурсивных уравнений — модель, которая содержит зависимые переменные (результативные) одних уравнений в роли фактора, оказываясь в правой части других уравнений.
Мультипликативная модель – модель, в которой временной ряд представлен как произведение перечисленных компонент.
Несмещенная оценка — оценка, среднее которой равно самой оцениваемой величине.
Нулевая гипотеза — предположение о том, что результат не зависит от фактора (коэффициент регрессии равен нулю).
Обобщенный метод наименьших квадратов (ОМНК) — метод, который не требует постоянства дисперсии (гомоскедастичности) остатков, но предполагает пропорциональность остатков общему множителю (дисперсии). Таким образом, это взвешенный МНК.
Объясненная дисперсия — показатель вариации результата, обусловленной регрессией.
Объясняемая (результативная) переменная — переменная, которая статистически зависит от факторной переменной, или объясняющей (регрессора).
Остаточная дисперсия — необъясненная дисперсия, которая показывает вариацию результата под влиянием всех прочих факторов, неучтенных регрессией.
Предопределенные переменные — это экзогенные переменные системы и лаговые эндогенные переменные системы.
Приведенная форма системы — форма, которая, в отличие от структурной, уже содержит одни только линейно зависящие от экзогенных переменных эндогенные переменные. Внешне ничем не отличается от системы независимых уравнений.
Расчетное значение F-отношения — значение, которое получают делением объясненной дисперсии на 1 степень свободы на остаточную дисперсию на 1 степень свободы.
Регрессия (зависимость) — это усредненная (сглаженная), т.е. свободная от случайных мелкомасштабных колебаний (флуктуаций), квазидетерминированная связь между объясняемой переменной (переменными) и объясняющей переменной (переменными). Эта связь выражается формулами, которые характеризуют функциональную зависимость и не содержат явно стохастических (случайных) переменных, которые свое влияние теперь оказывают как результирующее воздействие, принимающее вид чисто функциональной зависимости.
Регрессор (объясняющая переменная, факторная переменная) — это независимая переменная, статистически связанная с результирующей переменной. Характер этой связи и влияние изменения (вариации) регрессора на результат исследуются в эконометрике.
Система взаимосвязанных уравнений — это система одновременных или взаимозависимых уравнений. В ней одни и те же переменные выступают одновременно как зависимые в одних уравнениях и в то же время независимые в других. Это структурная форма системы уравнений. К ней неприменим МНК.
Система внешне не связанных между собой уравнений — система, которая характеризуется наличием одних только корреляций между остатками (ошибками) в разных уравнениях системы.
Случайный остаток (отклонение) — это чисто случайный процесс в виде мелкомасштабных колебаний, не содержащий уже детерминированной компоненты, которая имеется в регрессии.
Состоятельные оценки — оценки, которые позволяют эффективно применять доверительные интервалы, когда вероятность получения оценки на заданном расстоянии от истинного значения параметра становится близка к 1, а точность самих оценок увеличивается с ростом объема выборки.
Спецификация модели — определение существенных факторов и выявление мультиколлинеарности.
Стандартная ошибка — среднеквадратичное (стандартное) отклонение. Оно связано со средней ошибкой и коэффициентом доверия.
Степени свободы — это величины, характеризующие число независимых параметров и необходимые для нахождения по таблицам распределений их критических значений.
Тренд — основная тенденция развития, плавная устойчивая закономерность изменения уровней ряда.
Уровень значимости — величина, показывающая, какова вероятность ошибочного вывода при проверке статистической гипотезы по статистическому критерию.
Фиктивные переменные — это переменные, которые отражают сезонные компоненты ряда для какого-либо одного периода.
Эконометрическая модель — это уравнение или система уравнений, особым образом представляющие зависимость (зависимости) между результатом и факторами. В основе эконометрической модели лежит разбиение сложной и малопонятной зависимости между результатом и факторами на сумму двух следующих компонентов: регрессию (регрессионная компонента) и случайный (флуктуационный) остаток. Другой класс эконометрических моделей образует временные ряды.
Эффективность оценки — это свойство оценки обладать наименьшей дисперсией из всех возможных.
источники:
http://studrb.ru/works/entry29502WbDxMY
http://damirock.com/exam/math/otvetyi-na-testyi-po-ekonometrike/
Контрольная работа 1
Задания для выполнения контрольной работы № 1
Исследовать динамику экономического показателя на основе анализа одномерного временного ряда
В течение девяти последовательных недель фиксировался спрос Y(t) (млн. р.) на кредитные ресурсы финансовой компании. Временной ряд Y(t) этого показателя приведен ниже в таблице
Таблица 1 — Динамика спроса на кредитные ресурсы финансовой компании
Номер наблюдения ( t = 1,2,…,9)
1 2 3 4 5 6 7 8 9
5 7 10 12 15 18 20 23 26
Требуется:
1) Проверить наличие тренда графическим методом с использованием Мастера диаграмм. Сделать вывод. Построить линейную модель , параметры которой оценить МНК ( — расчетные, смоделированные значения временного ряда):
a) с использованием Анализа данных;
b) с использованием Поиска решений;
c) с использованием матричных функций;
d) с использованием функции ЛИНЕЙН.
Дать экономическую интерпретацию параметрам модели.
2) Оценить адекватность модели, используя свойства независимости остаточной компоненты, случайности и соответствия нормальному закону распределения (при использовании R/S-критерия взять табулированные границы 2,7—3,7). Оценить точность модели с помощью средней относительной ошибки аппроксимации.
3) Осуществить прогноз спроса на следующие две недели (доверительный интервал прогноза рассчитать при доверительной вероятности р = 80%). Указать ширину доверительного интервала. Привести график.
Контрольная работа 2
Задания для выполнения контрольной работы №2
На основании данных, приведенных в табл.3:
1. Постройте диаграммы рассеяния, представляющие собой зависимости Y от каждого из факторов Х. Сделайте выводы о характере взаимосвязи переменных. Вычислите матрицу коэффициентов парной корреляции, проверьте значимость коэффициентов корреляции.
2. Осуществите двумя способами выбор факторных признаков для построения регрессионной модели:
а) на основе анализа матрицы коэффициентов парной корреляции;
б) с помощью пошагового отбора методом исключения.
и постройте уравнения множественной регрессии в линейной форме с выбранными факторами. Выберите лучшую модель. Дайте экономическую интерпретацию коэффициентов модели регрессии.
3. Дайте сравнительную оценку силы связи факторов с результатом с -коэффициентов.- и помощью коэффициентов эластичности,
4. Используя результаты регрессионного анализа ранжируйте компании по степени эффективности
Для варианта 5:
Номер строки Факторы
3-52 Х1 Х3 Х4 Х5 Х6
Таблица 3 — Исходные данные по компаниям
Добыча сырой нефти и природного газа; предоставление услуг в этих областях № п/п При-быль (убы-ток) Долгосроч-ные обяза-тельства Оборот-ные акти-вы Основ-ные средства Дебиторская задолжен-ность (крат-косрочная) Запасы готовой продукции и товаров для пере-продажи
у х1 х3 х4 х5 х6
Акмай, ОАО 3 13612 20268 18903 81072 8678 84
Аксоль, ОАО, произ-водственнокоммерческая фирна 4 964 211 13398 8446 4821 0
………….
50 40997 101706 79930 178604 58762 1035
51 1580624 9285230 1553508 6546853 259519 13516
52 9990896 1645470 26312477 2329554 7271400 391744