Гоночный автомобиль проехал 15 кругов по трассе функция k n показывает за сколько минут автомобиль

Часы со стрелками показывают 8 часов ровно. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

До четвертой встречи стрелок минутная должна сначала пройти 8 разделяющих их часовых делений (поскольку часы показывают 8 часов), затем 3 раза обойти полный круг, то есть пройти 36 часовых делений, и пройти последние L делений, на которые поворачивается часовая стрелка за время движения минутной. Скорость движения минутной стрелки в 12 раз больше часовой: пока часовая обходит один полный круг, минутная проходит 12 кругов. Приравняем время движения часовой и минутной стрелок до их четвертой встречи:

Часовая стрелка пройдет 4 деления, что соответствует 4 часам, то есть 240 минутам.

Приведем арифметическое решение.

Скорость минутной стрелки 1 круг в час, а часовой — круга в час, поэтому скорость удаления или сближения стрелок равна круга в час. Расстояние между стрелками, отсчитываемое по окружности, в начальный момент составляет 40 минут или круга. С момента первой встречи до момента четвёртой встречи минутная стрелка должна опередить часовую на три круга. Всего круга. Поэтому необходимое время равно часа или 240 минут.

Приведем другое решение.

Ясно, что в первый раз стрелки встретятся между 8 и 9 часами, второй раз — между 9 и 10 часами, третий — между 10 и 11, четвертый — между 11 и 12 часами, то есть ровно в 12 часов. Таким образом, они встретятся ровно через 4 часа, что составляет 240 минут.

Помещаем решение в общем виде.

Скорость вращения часовой стрелки равна 0,5 градуса в минуту, а минутной — 6 градусов в минуту. Поэтому когда часы показывают время h часов m минут часовая стрелка повернута на 30h + 0,5m градусов, а минутная — на 6m градусов относительно 12-часового деления.

Пусть в первый раз стрелки встретятся через t₁ минут. Тогда если минутная стрелка еще не опережала часовую в течение текущего часа, то 6m + 6t₁ = 30h + 0,5m + 0,5t₁, т. е. t₁ = (60h − 11m)/11 (*). В противоположном случае получаем уравнение 6m + 6t₁ = 30h + 0,5m + 0,5t₁ + 360, откуда t₁ = (60h − 11m + 720)/11 (**).

Пусть во второй раз стрелки встретятся через t₂ минут после первого, тогда 0,5t₂ = 6t₂ − 360, откуда t₂ = 720/11 (***). Это же верно для каждого следующего оборота.

Поэтому для встречи с номером n из (*) и (**) с учетом (***) имеем соответственно: t_n = (60h − 11m + 720(n − 1))/11 или t_n = (60h − 11m + 720n − 720)/11.

Источник

Задачи ЕГЭ на движение по окружности

Секрет задач на движение по окружности: тот, кто обгоняет, проезжает на 1 круг больше, если это первый обгон. И на n кругов больше, если обогнал другого в n-ный раз.

Из одной точки круговой трассы, длина которой равна 8 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 114 км/ч, и через 20 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.

Автомобили стартовали одновременно, и первый автомобиль через 20 минут после старта опережал второй автомобиль на один круг. Значит, за эти 20 минут, то есть за часа он проехал на 1 круг больше – то есть на 8 км больше.

Из пункта круговой трассы выехал велосипедист, а через минут следом за ним отправился мотоциклист. Через минут после отправления он догнал велосипедиста в первый раз, а еще через минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна км. Ответ дайте в км/ч.

Запишем эти данные в таблицу:

Затем мотоциклист второй раз обогнал велосипедиста. Произошло это через минут, то есть через часа после первого обгона.

Нарисуем вторую таблицу.

А какие же расстояния они проехали? Мотоциклист обогнал велосипедиста. Значит, он проехал на один круг больше. Это и есть секрет данной задачи. Один круг — это длина трассы, она равна км. Получим второе уравнение:

Решим получившуюся систему.

Часы со стрелками показывают часов минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Минутная стрелка пройдет на круга больше, поэтому уравнение будет таким:

Решив его, получим, что часа. Итак, через часа стрелки поравняются во второй раз, еще через часа — в третий, и еще через часа — в четвертый.

Ответ полностью согласуется с «экспериментальным» решением! 🙂

На экзамене по математике вам может также встретиться задача о нахождении средней скорости. Запомним, что средняя скорость не равна среднему арифметическому скоростей. Она находится по специальной формуле:

Если участков пути было два, то

А сейчас покажем вам один из секретов решения текстовых задач. Что делать, если у вас получился в уравнении пятизначный дискриминант? Да, это реальная ситуация! Это может встретиться в варианте ЕГЭ.

Два гонщика участвуют в гонках. Им предстоит проехать 60 кругов по кольцевой трассе протяжённостью 3 км. Оба гонщика стартовали одновременно, а на финиш первый пришёл раньше второго на 10 минут. Чему равнялась средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 15 минут? Ответ дайте в км/ч.

Первый гонщик через 15 минут после старта обогнал второго на 1 круг. Значит, за 15 минут он проехал на 1 круг, то есть на 3 километра больше. За час он проедет на километров больше. Его скорость на 12 км/ч больше, чем скорость второго.

Как всегда, составляем таблицу и уравнение. 10 минут переведем в часы. Это часа.

Честно преобразовав это уравнение к квадратному, получим:

Пятизначный дискриминант, вот повезло! Но есть и другой способ решения, и он намного проще.
Посмотрим еще раз на наше уравнение:

Заметим, что 180 делится на 12. Сделаем замену:

Это уравнение легко привести к квадратному и решить.
Целый положительный корень этого уравнения: Тогда

Мы решили текстовую задачу с помощью замены переменной. Этот прием в математике используется везде: в решении задач, уравнений и неравенств, в задачах с параметрами и интегрировании. Общее правило: можете сделать замену переменной – сделайте.

Источник

Гоночный автомобиль проехал 15 кругов по трассе функция k n показывает

Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?

Пусть v км/ч — скорость первого мотоциклиста, тогда скорость второго мотоциклиста равна v + 21 км/ч. Пусть первый раз мотоциклисты поравняются через часов. Для того, чтобы мотоциклисты поравнялись, более быстрый должен преодолеть изначально разделяющее их расстояние, равное половине длины трассы. Поэтому

Таким образом, мотоциклисты поравняются через часа или через 20 минут.

Приведём другое решение.

Быстрый мотоциклист движется относительно медленного со скоростью 21 км в час, и должен преодолеть разделяющие их 7 км. Следовательно, на это ему потребуется одна треть часа.

Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.

Пусть скорость второго автомобиля равна км/ч. За 2/3 часа первый автомобиль прошел на 14 км больше, чем второй, отсюда имеем

Добрый день, на мой взгляд, гораздо проще сменить систему отсчёта( Найдём скорость удаления(21) и (80-21=59).

Из пункта A круговой трассы выехал велосипедист. Через 30 минут он еще не вернулся в пункт А и из пункта А следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.

К моменту первого обгона мотоциклист за 10 минут проехал столько же, сколько велосипедист за 40 минут, следовательно, его скорость в 4 раза больше. Поэтому, если скорость велосипедиста принять за x км/час, то скорость мотоциклиста будет равна 4x, а скорость их сближения — 3x км/час.

C другой стороны, второй раз мотоциклист догнал велосипедиста за 30 минут, за это время он проехал на 30 км больше. Следовательно, скорость их сближения составлят 60 км/час.

Итак, 3х = 60 км/час, откуда скорость велосипедиста равна 20 км/час, а скорость мотоциклиста равна 80 км/час.

Вы утвер­жда­е­те что вто­рой раз мо­то­цик­лист до­гнал ве­ло­си­пе­ди­ста за 30 минут и за это время он про­ехал на 30 км боль­ше. Сле­до­ва­тель­но, ско­рость их сбли­же­ния со­став­лят 60 км/час, но это озна­ча­ет, что ве­ло­си­пе­дист остановился в той точке, где мо­то­цик­лист до­гнал его пер­вый раз, и оста­вал­ся в ней неподвижно, пока мо­то­цик­лист про­ез­жал круг и возвращался в эту точку. Но на самом-то деле ве­ло­си­пе­дист дви­гал­ся 30 мин, пока мо­то­цик­лист про­ез­жал круг. Зна­чит, чтобы мо­то­цик­лист до­гнал ве­ло­си­пе­ди­ста мо­то­цик­ли­сту нужно проехать 30 км + рас­сто­я­ние, ко­то­рое про­шел ве­ло­си­пе­дист, пока дви­гал­ся мотоциклист.

Вы правы в том, что они двигались одновременно и второй раз встретились в другой точке. Это не противоречит сказанному в решении: при этом мотоциклист проехал на 30 км больше.

Часы со стрелками показывают 8 часов ровно. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

До четвертой встречи стрелок минутная должна сначала пройти 8 разделяющих их часовых делений (поскольку часы показывают 8 часов), затем 3 раза обойти полный круг, то есть пройти 36 часовых делений, и пройти последние L делений, на которые поворачивается часовая стрелка за время движения минутной. Скорость движения минутной стрелки в 12 раз больше часовой: пока часовая обходит один полный круг, минутная проходит 12 кругов. Приравняем время движения часовой и минутной стрелок до их четвертой встречи:

Часовая стрелка пройдет 4 деления, что соответствует 4 часам, то есть 240 минутам.

Приведем арифметическое решение.

Скорость минутной стрелки 1 круг в час, а часовой — круга в час, поэтому скорость удаления или сближения стрелок равна круга в час. Расстояние между стрелками, отсчитываемое по окружности, в начальный момент составляет 40 минут или круга. С момента первой встречи до момента четвёртой встречи минутная стрелка должна опередить часовую на три круга. Всего круга. Поэтому необходимое время равно часа или 240 минут.

Приведем другое решение.

Ясно, что в первый раз стрелки встретятся между 8 и 9 часами, второй раз — между 9 и 10 часами, третий — между 10 и 11, четвертый — между 11 и 12 часами, то есть ровно в 12 часов. Таким образом, они встретятся ровно через 4 часа, что составляет 240 минут.

Помещаем решение в общем виде.

Скорость вращения часовой стрелки равна 0,5 градуса в минуту, а минутной — 6 градусов в минуту. Поэтому когда часы показывают время h часов m минут часовая стрелка повернута на 30h + 0,5m градусов, а минутная — на 6m градусов относительно 12-часового деления.

Пусть в первый раз стрелки встретятся через t₁ минут. Тогда если минутная стрелка еще не опережала часовую в течение текущего часа, то 6m + 6t₁ = 30h + 0,5m + 0,5t₁, т. е. t₁ = (60h − 11m)/11 (*). В противоположном случае получаем уравнение 6m + 6t₁ = 30h + 0,5m + 0,5t₁ + 360, откуда t₁ = (60h − 11m + 720)/11 (**).

Пусть во второй раз стрелки встретятся через t₂ минут после первого, тогда 0,5t₂ = 6t₂ − 360, откуда t₂ = 720/11 (***). Это же верно для каждого следующего оборота.

Поэтому для встречи с номером n из (*) и (**) с учетом (***) имеем соответственно: t_n = (60h − 11m + 720(n − 1))/11 или t_n = (60h − 11m + 720n − 720)/11.

Источник

Гоночный автомобиль проехал 15 кругов по трассе функция k n показывает

Два гонщика участвуют в гонках. Им предстоит проехать 45 кругов по кольцевой трассе протяжённостью 5,4 км. Оба гонщика стартовали одновременно, а на финиш первый пришёл раньше второго на 27 минут. Чему равнялась средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 18 минут? Ответ дайте в км/ч.

Это задание ещё не решено, приводим решение прототипа.

Два гонщика участвуют в гонках. Им предстоит проехать 60 кругов по кольцевой трассе протяжённостью 3 км. Оба гонщика стартовали одновременно, а на финиш первый пришёл раньше второго на 10 минут. Чему равнялась средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 15 минут? Ответ дайте в км/ч.

Первый обогнал второго на 3 км за четверть часа, это значит, что скорость удаления (сближения) гонщиков равна км/ч. Обозначим скорость второго гонщика км/ч, тогда скорость первого км/ч. Составим и решим уравнение:

Таким образом, скорость второго гонщика равна 108 км/ч.

Источник

Гоночный автомобиль проехал 15 кругов по трассе функция k n показывает

Автомобиль массой 2 т проезжает верхнюю точку выпуклого моста, двигаясь с постоянной по модулю скоростью 36 км/ч. Радиус кривизны моста равен 40 м. Из приведённого ниже списка выберите все правильные утверждения, характеризующих движение автомобиля по мосту.

1) Равнодействующая сил, действующих на автомобиль в верхней точке моста, сонаправлена с его скоростью.

2) Сила, с которой мост действует на автомобиль в верхней точке моста, меньше 20 000 Н и направлена вертикально вниз.

3) В верхней точке моста автомобиль действует на мост с силой, равной 15 000 Н.

5) Ускорение автомобиля в верхней точке моста направлено противоположно его скорости.

Переведем скорость

Рассмотрим рисунок, поясняющий движение автомобиля по выпуклому мосту.

1. Неверно. Равнодействующая сил реакции опоры N и силы тяжести mg по второму закону Ньютона сонаправлена с вектором ускорения. А т. к. автомобиль движется по окружности, то ускорение направлено к центру окружности, т. е. вниз. Следовательно, и равнодействующая направлена вниз. Скорость автомобиля при движении по окружности направлена по касательной (в данном случае — горизонтально).

2. Неверно. Сила, с которой мост действует на автомобиль — сила реакции опоры — направлена вертикально вверх.

3. Верно. Сила, с которой автомобиль действует на мост, равна весу тела. По третьему закону Ньютона P = N. Найдём силу реакции опоры по второму закону Ньютона Центростремительное ускорение равно Значит, Р = 15 кН.

4. Верно. (см. пункт 3).

5. Неверно. Вектор ускорения направлен вертикально вниз, вектор скорости — горизонтально (см. пункт 1).

Источник

Гоночный автомобиль может достигать скорости 220 км / ч.

За какое время такой автомобиль преодолеет 500 м?

t = S / V = 500 / 61 = 8 c

После старта гоночный автомобиль за 25 секунд достиг скорости 360 км / ч?

После старта гоночный автомобиль за 25 секунд достиг скорости 360 км / ч.

Определите расстояние пройдённое автомобилем за это время.

Скорость автобуса 20 м / с, а скорость гоночного автомобиля 360км / ч?

Скорость автобуса 20 м / с, а скорость гоночного автомобиля 360км / ч.

Во сколько раз скорость гоночного автомобиля больше скорости автобуса?

Скорость света в пустоте 300000 км / с, а рекордная скорость гоночного автомобиля 1000 км / ч?

Скорость света в пустоте 300000 км / с, а рекордная скорость гоночного автомобиля 1000 км / ч.

Во сколько раз скорость света больше скорости гоночного автомобиля?

После старта гоночный автомобиль приобрёл скорость 90км / ч в течении 10 секунд?

После старта гоночный автомобиль приобрёл скорость 90км / ч в течении 10 секунд.

Какое расстояние он прошёл за это время?

Автомобиль двигается со скоростью 108 км / ч в течение 30 минут?

Автомобиль двигается со скоростью 108 км / ч в течение 30 минут.

Какое расстояние преодолеет автомобиль за это время?

Пишите ответ подробно!

Автомобиль массой 1000 кг разгоняется с места и достигает скорости 20м / с?

Автомобиль массой 1000 кг разгоняется с места и достигает скорости 20м / с.

Какое время ему для этого понадобилось, если равнодействующая всех сил действующих на автомобиль равна 500 Н.

Автомобиль за время 10 мин, проехал расстояние 11км?

Автомобиль за время 10 мин, проехал расстояние 11км.

Какой путь он преодолеет за 45 мин двигаясь с той же скоростью?

Выразите скорость автомобиля в километров в час.

Автомобиль массой 1000 кг разогнался с места и достигает скорости 20 м / с?

Автомобиль массой 1000 кг разогнался с места и достигает скорости 20 м / с.

Какое время ему для этого понадобилось, если равнодействующая всех сил, действующих на автомобиль, равна 500H?

Автомобиль за время 10 минут проехал расстояние 11 к?

Автомобиль за время 10 минут проехал расстояние 11 к.

Какой путь он преодолеет за 45 минут, двигаясь с той же скоростью?

Выразите скорость автомобиля в километрах в час.

Q = 3 * 10(10) ДжПри изохорном процессеобъем не меняетсяработа равна = 0 ДжQ = A + dU = 0 + dUdU = Q = 3 * 10(10) Дж.

Радиус блока R. Чему равен момент силы F1 и F2 относительно точки А? Если F1 = 6 H то чему равна сила F2 чтобы блок оставался неподвижным? = = = M1 = R * F1 M2 = 2 * R * F2 = = = M1 = M2 F2 = F1 / 2 = 6 / 2 = 3 H (рисунок в приложении) = = = = = =..

Модуль перемещения равен расстоянию от точки бросания до точки падения S = 40 м (если только тело бросали с уровня поверхности земли).

Тело упало на расстоянии 40 м от точки бросания. Это и есть модуль перемещения ISI = 40 м.

КПД = Q / Qз Q = КПД * Qз Qз = А = F * s т. К. движение равномерное, то F = Fтр = μ * m * g s = υ * t Q = КПД * μ * m * g * υ * t Q = 0. 4 * 0. 005 * 2000000 кг * 9, 8 м / с2 * 20 м / с * 300 с = 235200000 Дж = 235, 2 МДж.

1. 1)15 см 2) 4 с 3) 0, 25 Гц 4) pi(число Пи) / 2 5) x = 0, 15 * cos((pi / 2)t) 2. 1)10 ^ 5 2) 0. 04 c 3) 25 Гц 4) 50pi Вроде так.

Источник

Прямолинейное равноускоренное движение. Ускорение, скорость, перемещение

Решебник к сборнику задач по физике для 7- 9 классов, Перышкин А.В.

1439. Мотоцикл в течение 5 с может увеличить скорость от 0 до 72 км/ч. Определите ускорение мотоцикла.

1440. Определите ускорение лифта в высотном здании, если он увеличивает свою скорость на 3,2 м/с в течение 2 с.

1441. Автомобиль, двигавшийся со скоростью 72 км/ч, равномерно тормозит и через 10 с останавливается. Каково ускорение автомобиля?

1442. Как назвать движения, при которых ускорение постоянно? равно нулю?
Равноускоренное, равномерное.

1443. Санки, скатываясь с горы, движутся равноускоренно и в конце третьей секунды от начала движения имеют скорость 10,8 км/ч. Определите, с каким ускорением движутся санки.

1445. Мотоцикл «Хонда», двигавшийся со скоростью 90 км/ч, начал равномерно тормозить и через 5 с сбросил скорость до 18 км/ч. Каково ускорение мотоцикла?

1446. Объект из состояния покоя начинает двигаться с постоянным ускорением, равным 6 • 10-3 м/с2. Определите скорость через 5 мин после начала движения. Какой путь прошел объект за это время?

1447. Яхту спускают на воду по наклонным стапелям. Первые 80 см она прошла за 10 с. За какое время яхта прошла оставшиеся 30 м, если ее движение оставалось равноускоренным?

1448. Грузовик трогается с места с ускорением 0,6 м/с2. За какое время он пройдет путь в 30 м?

1449. Электричка отходит от станции, двигаясь равноускоренно в течение 1 мин 20 с. Каково ускорение электрички, если за это время ее скорость стала 57,6 км/ч? Какой путь она прошла за указанное время?

1450. Самолет для взлета равноускоренно разгоняется в течение 6 с до скорости 172,8 км/ч. Найдите ускорение самолета. Какое расстояние прошел самолет при разгоне?

1451. Товарный поезд, трогаясь с места, двигался с ускорением 0,5 м/с2 и разогнался до скорости 36 км/ч. Какой путь он при этом прошел?

1452. От станции равноускоренно тронулся скорый поезд и, пройдя 500 м, достиг скорости 72 км/ч. Каково ускорение поезда? Определите время его разгона.

1454. Электричка, шедшая со скоростью 72 км/ч, начала тормозить с постоянным ускорением, равным по модулю 2 м/с2. Через какое время она остановится? Какое расстояние она пройдет до полной остановки?

1455. Городской автобус двигался равномерно со скоростью 6 м/с, а затем начал тормозить с ускорением, по модуля равным 0,6 м/с2. За какое время до остановки и на каком расстоянии от нее надо начать торможение?

1456. Санки скользят по ледяной дорожке с начальной скоростью 8 м/с, и за каждую секунду их скорость уменьшается на 0,25 м/с. Через какое время санки остановятся?

1457. Мотороллер, двигавшийся со скоростью 46,8 км/ч, останавливается при равномерном торможении в течение 2 с. Каково ускорение мотороллера? Каков его тормозной путь?

1458. Теплоход, плывущий со скоростью 32,4 км/ч, стал равномерно тормозить и, подойдя к пристани через 36 с, полностью остановился. Чему равно ускорение теплохода? Какой путь он прошел за время торможения?

1459. Товарняк, проходя мимо шлагбаума, приступил к торможению. Спустя 3 мин он остановился на разъезде. Какова начальная скорость товарняка и модуль его ускорения, если шлагбаум находится на расстоянии 1,8 км от разъезда?

1460. Тормозной путь поезда 150 м, время торможения 30 с. Найдите начальную скорость поезда и его ускорение.

1461. Электричка, двигавшаяся со скоростью 64,8 км/ч, после начала торможения до полной остановки прошла 180 м. Определите ее ускорение и время торможения.

1462. Аэроплан летел равномерно со скоростью 360 км/ч, затем в течение 10 с он двигался равноускоренно: его скорость возрастала на 9 м/с за секунду. Определите, какую скорость приобрел аэроплан. Какое расстояние он пролетел при равноускоренном движении?

1463. Мотоцикл, двигавшийся со скоростью 27 км/ч, начал равномерно ускоряться и через 10 с достиг скорости 63 км/ч. Определите среднюю скорость мотоцикла при равноускоренном движении. Какой путь он проехал за время равноускоренного движения?

1464. Прибор отсчитывает промежутки времени, равные 0,75 с. Шарик скатывается с наклонного желоба в течение трех таких промежутков времени. Скатившись с наклонного желоба, он продолжает двигаться по горизонтальному желобу и проходит в течение первого промежутка времени 45 см. Определите мгновенную скорость шарика в конце наклонного желоба и ускорение шарика при движении по этому желобу.

1465. Отходя от станции, поезд движется равноускоренно с ускорением 5 см/с2. По прошествии какого времени поезд приобретает скорость 36 км/ч?

1466. При отправлении поезда от станции его скорость в течение первых 4 с возросла до 0,2 м/с, в течение следующих 6 с еще на 30 см/с и за следующие 10 с на 1,8 км/ч. Как двигался поезд в течение этих 20 с?

1467. Санки, скатываясь с горы, движутся равноускоренно. На некотором участке пути скорость санок в течение 4 с возросла от 0,8 м/с до 14,4 км/ч. Определите ускорение санок.

1468. Велосипедист начинает двигаться с ускорением 20 см/с2. По истечении какого времени скорость велосипедиста будет равна 7,2 км/ч?

1469. На рисунке 184 дан график скорости некоторого равноускоренного движения. Пользуясь масштабом, данным на рисунке, определите путь, проходимый в этом движении в течение 3,5 с.

1470. На рисунке 185 изображен график скорости некоторого переменного движения. Перечертите рисунок в тетрадь и обозначьте штриховкой площадь, численно равную пути, проходимому в течение 3 с. Чему примерно равен этот путь?

1471. В течение первого промежутка времени от начала равноускоренного движения шарик проходит по желобу 8 см. Какое расстояние пройдет шарик в течение трех таких же промежутков, прошедших от начала движения?

1472. В течение 10 равных промежутков времени от начала движения тело, двигаясь равноускоренно, прошло 75 см. Сколько сантиметров прошло это тело в течение двух первых таких же промежутков времени?

1473. Поезд, отходя от станции, движется равноускоренно и в течение двух первых секунд проходит 12 см. Какое расстояние пройдет поезд в течение 1 мин, считая от начала движения?

1474. Поезд, отходя от станции, движется равноускоренно с ускорением 5 см/с2. Сколько времени потребуется для развития скорости 28,8 км/ч и какое расстояние пройдет поезд за это время?

1475. Паровоз по горизонтальному пути подходит к уклону со скоростью 8 м/с, затем движется вниз по уклону с ускорением 0,2 м/с. Определите длину уклона, если паровоз проходит его за 30 с.

1476. Начальная скорость тележки, движущейся вниз по наклонной доске, равна 10 см/с. Всю длину доски, равную 2 м, тележка прошла в течение 5 сек. Определите ускорение тележки.

1477. Пуля вылетает из ствола ружья со скоростью 800 м/с. Длина ствола 64 см. Предполагая движение пули внутри ствола равноускоренным, определите ускорение и время движения.

1478. Автобус, двигаясь со скоростью 4 м/с, начинает равномерно ускоряться на 1 м/с за секунду. Какой путь пройдет автобус за шестую секунду?

1479. Грузовик, имея некоторую начальную скорость, начал двигаться равноускоренно: за первые 5 с прошел 40 м, а за первые 10 с — 130 м. Найдите начальную скорость грузовика и его ускорение.

1480. Катер, отходя от пристани, начал равноускоренное движение. Пройдя некоторое расстояние, он достиг скорости 20 м/с. Какова была скорость катера в тот момент, когда он проплыл половину этого расстояния?

1481. Лыжник скатывается с горы с нулевой начальной скоростью. На середине горы его скорость была 5 м/с, через 2 с скорость стала 6 м/с. Считая, что она увеличивается равномерно, определите скорость лыжника через 8 с после начала движения.

1482. Автомобиль тронулся с места и двигается равноускоренно. За какую секунду от начала движения путь, пройденный автомобилем, вдвое больше пути, пройденного им в предыдущую секунду?

1483. Найдите путь, пройденный телом за восьмую секунду движения, если оно начинает двигаться равноускоренно без начальной скорости и за пятую секунду проходит путь 27 м.

1484. Провожающие стоят у начала головного вагона поезда. Поезд трогается и движется равноускоренно. За 3 с весь головной вагон проходит мимо провожающих. За какое время пройдет мимо провожающих весь поезд, состоящий из 9 вагонов?

1485. Материальная точка движется по закону x = 0,5t². Какое это движение? Каково ускорение точки? Постройте график зависимости от времени:
а) координаты точки;
б) скорости точки;
в) ускорения.

1486. Поезд остановился через 20 с после начала торможения, пройдя за это время 120 м. Определите первоначальную скорость поезда и ускорение поезда.

1487. Поезд, идущий со скоростью 18 м/с, начал тормозить, и через 15 с остановился. Считая движение поезда при торможении равнозамедленным, определите путь, пройденный поездом за эти 15 с.

1488. Постройте графики скорости равнозамедленного движения для случаев:
1) V0 = 10 м/с, а = — 1,5 м/с2;
2) V0 = 10 м/с; а = — 2 м/с2.
Масштаб в обоих случаях одинаков: 0,5 см – 1 м/с; о,5 см – 1 сек.

1489. Изобразите пройденный путь за время t на графике скорости равнозамедленного движения. Принять V0 = 10 м/с, а = 2 м/с2.

1490. Опишите движения, графики скоростей которых даны на рисунке 186, а и б.
а) движение будет равнозамедленным;
б) сначала тело будет двигаться равноускоренно, затем равномерно. На 3м участке движение будет равнозамедленное.

Источник

Гоночный автомобиль может достичь скорости 220 км ч

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав 0,8 километра. Задача сводится к решению уравнения при известном значении длины пути км:

Найдём, при каком ускорении автомобиль достигнет требуемой скорости, проехав 0,8 километра. Задача сводится к решению уравнения при известном значении длины пути км:

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав 0,7 километра. Задача сводится к решению уравнения при известном значении длины пути км:

Я не понял! Этот гонщик у вас на космическом корабле что ли гоняет?

Все в порядке с ним. Выразите ускорение в метрах в секунду в квадрате, сами убедитесь.

Выразим ускорение из формулы для скорости и найдём его:

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав 1,1 км. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Источник

Гоночный автомобиль проехал трассу так что скорость менялась таким образом как показано на рисунке

Автомобиль массой 2 т проезжает верхнюю точку выпуклого моста, двигаясь с постоянной по модулю скоростью 36 км/ч. Радиус кривизны моста равен 40 м. Из приведённого ниже списка выберите все правильные утверждения, характеризующих движение автомобиля по мосту.

1) Равнодействующая сил, действующих на автомобиль в верхней точке моста, сонаправлена с его скоростью.

2) Сила, с которой мост действует на автомобиль в верхней точке моста, меньше 20 000 Н и направлена вертикально вниз.

3) В верхней точке моста автомобиль действует на мост с силой, равной 15 000 Н.

5) Ускорение автомобиля в верхней точке моста направлено противоположно его скорости.

Переведем скорость

Рассмотрим рисунок, поясняющий движение автомобиля по выпуклому мосту.

1. Неверно. Равнодействующая сил реакции опоры N и силы тяжести mg по второму закону Ньютона сонаправлена с вектором ускорения. А т. к. автомобиль движется по окружности, то ускорение направлено к центру окружности, т. е. вниз. Следовательно, и равнодействующая направлена вниз. Скорость автомобиля при движении по окружности направлена по касательной (в данном случае — горизонтально).

2. Неверно. Сила, с которой мост действует на автомобиль — сила реакции опоры — направлена вертикально вверх.

3. Верно. Сила, с которой автомобиль действует на мост, равна весу тела. По третьему закону Ньютона P = N. Найдём силу реакции опоры по второму закону Ньютона Центростремительное ускорение равно Значит, Р = 15 кН.

4. Верно. (см. пункт 3).

5. Неверно. Вектор ускорения направлен вертикально вниз, вектор скорости — горизонтально (см. пункт 1).

Источник

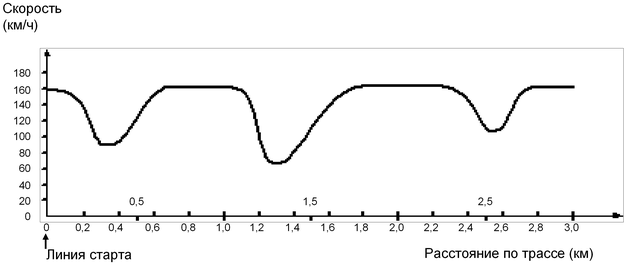
Скорость гоночной машины

На графике показано, как изменялась скорость гоночной машины, когда она проходила второй круг по трехкилометровой кольцевой трассе без подъемов и спусков.

Вопрос 1. Чему примерно равно расстояние от линии старта до начала самого длинного прямолинейного участка трассы?

A.

0,5 км

B.

1,5 км

C.

2,3 км

D.

2,6 км

Решение. При выезде на прямолинейный участок трассы машина сначала разгоняется до максимальной скорости, затем продолжает движение с набранной скоростью и в конце участка машина притормаживает, чтобы вписаться в поворот. Причем, чем длиннее прямолинейный участок, тем больше продолжается движение с максимальной скоростью.
Из графика видно, что дольше всего максимальная скорость сохранялась между 1,8 и 2,3 км. Значит, эта часть графика соответствует самому длинному прямолинейному участку трассы, начало которого, выбирая из предложенных вариантов, находится в 1,5 км от линии старта.
Правильный ответ: B.

Вопрос 2. В каком месте трассы скорость машины была наименьшей при прохождении второго круга?

A.	На линии старта.	B.	Примерно на отметке 0,8 км.
C.	Примерно на отметке 1,3 км.	D.	Примерно посередине трассы.

Решение. Из графика видно, что наименьшая скорость машины при прохождении второго круга, равная 70 км/ч, была примерно на отметке 1,3 км.
Правильный ответ: C.

Вопрос 3. Что можно сказать о скорости машины при прохождении трассы между отметками 2,6 км и 2,8 км?

A.	Скорость машины оставалась постоянной.
B.	Скорость машины увеличивалась.
C.	Скорость машины уменьшалась.
D.	По данному графику невозможно определить изменение скорости машины.

Решение. Из Из графика видно, что скорость машины на этом участке увеличивалась со 110 до 160 км/ч.
Правильный ответ: B.

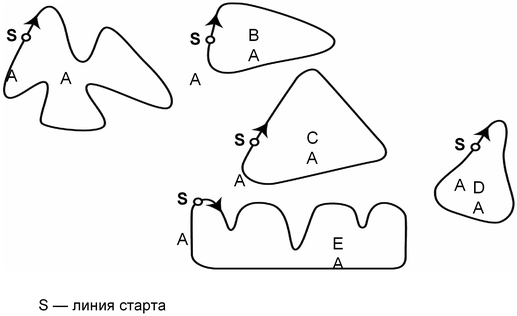
Вопрос 4. Ниже изображены пять различных по форме гоночных трасс:

По какой из этих трасс ехала гоночная машина, график скорости которой приведен ранее?
Решение. Судя по графику скорости, трасса содержит три прямолинейных участка: точка старта находится на самом коротком из них, далее идет средний по длине участок и затем самый длинный. Минимальная скорость у машины между средним и длинным участками, значит, между ними должен быть самый крутой поворот. Данным требованиям удовлетворяет форма трассы B.
Правильный ответ: B.

Источник

Гоночный автомобиль проехал трассу так что скорость менялась таким образом как показано на рисунке

На рисунке изображены графики зависимости модуля скорости движения четырёх автомобилей от времени. Один из автомобилей за первые 15 с движения проехал наибольший путь. Найдите этот путь. Ответ выразите в метрах.

Для того чтобы по графику модуля скорости найти путь, пройденный автомобилем за некоторый интервал времени, необходимо вычислить площадь под частью графика, соответствующей этому интервалу времени (в единицах произведения величин, отложенных по осям координат). Из приведенного рисунка видно, что максимальная площадь под графиком за первые 15 с, а значит, и максимальный путь на этом интервале времени, у автомобиля 3.

Найдём его путь, используя формулу для площади трапеции:

Извините, а как определить площадь под графиком 4?

В данной задаче нет необходимости ее подсчитывать, поскольку нас просят только сравнить пути (площади). Ясно, что для 4 площадь минимальна. Ежели поставить целью посчитать площадь, то это можно сделать приблизительно, посчитав по клеточкам (даже можно оценить погрешность такого подсчета).

То есть тут в принципе только визуальная составляющая работает?как то в точных науках так на глаз оценивать достаточно не привычно, но в тоже время легче.

В некотором роде любой эксперимент — это оценивание величин «на глаз». Когда Вы что-то измеряете линейкой, Вы смотрите, какое из делений ближе всего 🙂

Ускорение каждого можно найти по формуле a=(V1-V0)/t

Источник

Задачи

1. Средняя скорость из А в В.

Расстояние от пункта А до пункта В равно 45 км. Первую часть пути автомобиль ехал со скоростью в два раза меньше средней, а вторую часть пути – со скоростью в два раза больше средней. Найдите длину первой части пути.

2.Опять средняя скорость

Треть всего пути автомобиль проехал с постоянной скоростью V1, затем треть всего времени он ехал с постоянной скоростью V2. Найдите среднюю скорость на всем пути, если она оказалась равна скорости на оставшемся участке.

Ответ: .

На рисунке приведен план гоночной трассы гонок. Длины участков трассы: L1 = 1,8 км, L2 = 1,0 км, L3 = 1,4 км, L4 = 1,2 км. Каждый гоночный автомобиль (болид) движется на соответствующих участках трассы со скоростями: V1 = 60 м/с, V2 = 50 м/с, V3 = 20 м/с, V4 = 40 м/с. При переходе машины с одного участка на другой ее скорость изменяется практически мгновенно. По правилам заезда расстояние вдоль трассы между болидами не должно быть меньше L0 = 200 м. Какое максимальное число n автомобилей может одновременно участвовать в гонке?

Два электромеханических зайца соревнуются в беге. Один из них питается от обычной батарейки, а другой от «Duraell». Заяц с обычной батарейкой прибежал к финишу на t1 = 6 с позже своего соперника. Тогда ему заменили обычную батарейку на «Energizer». Во втором забеге зайцы побежали по той же трассе. С новой батарейкой скорость зайца возросла в полтора раза, и он прибежал к финишу на t2 = 8 с раньше соперника. Найдите отношение скорости V2 второго зайца к скорости V1 первого зайца во время первого забега.

Ответ:.

5. Встречные поезда

Поезд-экспресс прошел за время t1 = 9 с мимо встречной электрички, двигавшейся с такой же скоростью и имевшей в два раза большую длину. За какое время t2 экспресс пройдет мимо встречного пассажирского поезда, который в два раза длиннее электрички и едет вдвое быстрее?

6. Две радиоуправляемые машинки ездят по прямолинейному полигону. Их скорости зависят от времени периодически (рис.). В момент времени t = 0 машины находились рядом. На какое максимальное расстояние S они удалятся друг от друга в процессе движения?

7.Средняя скорость из А в В и обратно

Из города А в город В автомобилист ехал с постоянной скоростью 80 км/ч. На обратном пути трасса была загружена, и он двигался со скоростью 30 км/ч столько же времени, сколько он затратил на движение в первой поездке, а вот отставшийся участок пути оказался свободным, и автомобиль двигался со скоростью 100 км/ч. Определите среднюю скорость автомобиля на всем пути от города А до В и обратно.

8. Звуковые сигналы

Два гоночных автомобиля мчатся навстречу друг другу с одинаковой скоростью. Один из водителей начинает подавать звуковые сигналы длительностью V1, при этом другой водитель определил их длительностью V2 = 0,8V1. Скорость звука c в воздухе постоянна и равна 333 м/с. С какой скоростью едут автомобили?

9.Встреча поезда с электричкой

Длинный поезд едет со скоростью V. По соседним путям его обгоняет электричка, скорость которой 72 км/ч. Машиниста электрички заметил, что он проехал мимл поезда за 100 с. На обратном пути электричка и поезд снова встретились. На этот раз оказалось, что время прохождения электрички мимо поезда равно 20 с. Какова скорость поезда?

10. Средняя скорость.

Автомобиль первую половину времени ехал со скоростью V1 = 80 км/ч, оставшееся время – со скоростью V2 = 40 км/ч. Найдите среднюю скорость автомобиля на второй половине его пути.

Две машины едут по прямому участку дороги навстречу друг другу. Графики зависимости ско-ростей машин от времени приве-дены на рисунках 1 и 2. Чему равна средняя скорость сближения машин за первые 10 минут? Считайте, что машины сначала были на очень большом расстоянии и не успели встретиться. Указание: средняя скорость сближения – это отношение изменения расстояния между машинами ко времени движения машин.

Мальчик смог переплыть реку за минимальное время. Ширина реки равна 100 м. Скорость мальчика относительно воды постоянна и равна 1 м/с. Зависимость скорости течения V от расстояния х до берега приведена на графике. На какое расстояние вниз по реке его снесло течением? Считать, что в любом месте реки скорость течения направлена вдоль берегов.

13.Среднее сближение – 2.

Две машины едут по прямолинейному участку дорогу навстречу друг другу. Графики зависимости скоростей машин от пройденного расстяония приведены на рисунках. Вначале расстояние между машинами было равно 20 км.

Чему равна средняя скорость машин до их встречи? С какой максимальной скоростью сближались машины? Сколько времени длилось сближение с максимальной скоростью?

Указание: средняя скорость сближения – это отношение изменения расстояния между машинами ко времени движения машин.

Ответ: 22,2 м/с, 40 м/с, 900 с.

Первую часть пути машина проехала со скоростью 2V, а вторую – со скоростью . В результате всего движения средняя скорость машины оказалась равна V. Во сколько раз вторая часть пути длиннее первой?

Ответ: .

Крокодил Гена развивает скорость 5 м/с, но пробежать с таком скоростью он может не более 100 метров. После этого у него остаются силы только на последний рывок длиной 10 метров со скоротью 10 м/с. Чебурашка умеет бегать со скоростью V. Какую минимальную дистанцию от крокодила должен соблюдать Чебурашка, чтобы Гена не смог его догнать? Рассмотреть случаи, когда и

16. Время относительно

Поезд проехал мост длиной l = 450 м за t1 = 45 с. Охранник, стоящий на мосту, заметил, что поезд двигался мимо него в течение t2 = 30 с. Какое время ехал по мосту пассажир, сидящий в вагоне поезда? Найдите длину поезда, скорость его движения, и определите во сколько раз длина поезда больше длины моста.

Внедорожник «Нива» может проехать расстояние l = 39 км, имея скорость на асфальте х1 = 100 км/ч, а на грунтовом участке х2 = 25 км/ч. Автомобиль BMW на той же дороге по асфальту разгоняется до х3 = 160 км/ч, но по грунтовке едет только со скоростью х4 = 10 км/ч. При какой длине грунтового участка время движения машин окажется одинаковым?

Источник

Гоночный автомобиль проехал трассу так что скорость менялась таким образом как показано на рисунке

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав 0,8 километра. Задача сводится к решению уравнения при известном значении длины пути км:

Найдём, при каком ускорении автомобиль достигнет требуемой скорости, проехав 0,8 километра. Задача сводится к решению уравнения при известном значении длины пути км:

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав 0,7 километра. Задача сводится к решению уравнения при известном значении длины пути км:

Я не понял! Этот гонщик у вас на космическом корабле что ли гоняет?

Все в порядке с ним. Выразите ускорение в метрах в секунду в квадрате, сами убедитесь.

Выразим ускорение из формулы для скорости и найдём его:

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав 1,1 км. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Это задание ещё не решено, приводим решение прототипа.

Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути км:

Источник