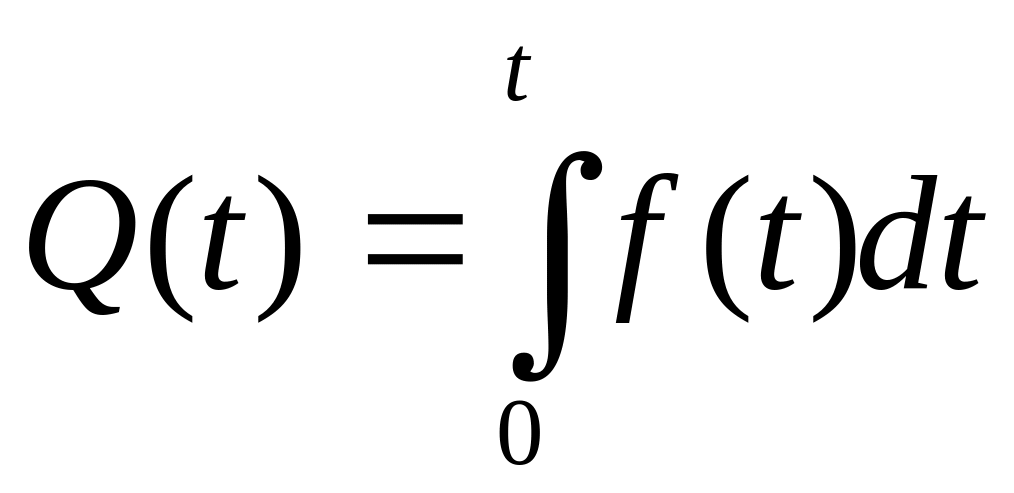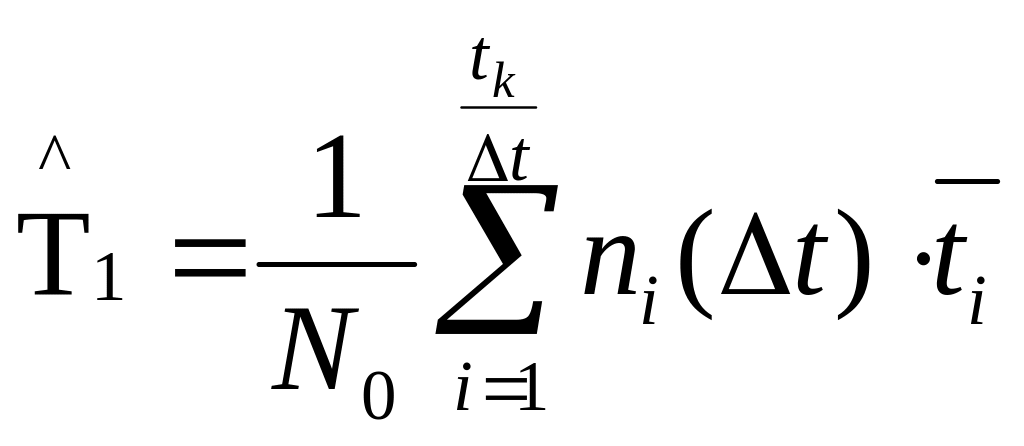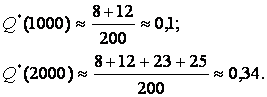Формула среднего времени безотказной работы в данной формуле характеризует

Средним временем безотказной работы называется математическое ожидание времени безотказной работы.

Эта характеристика надежности обозначается T. Как всякое математическое ожидание случайной величины среднее время безотказной работы определяется из выражения:

.                                            (1.25)

Приведенное определение является вероятностным. Для определения среднего времени безотказной работы из статистических данных пользуются формулой:

,                                                        (1.26)

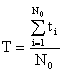
где t_i— время безотказной работы i-го образца, N₀— число образцов, над которыми проводится испытание.

Из выражения (1.26) видно, что для определения T необходимо знать моменты отказов всех образцов аппаратуры, над которыми проводится эксперимент. При большом числе образцов N₀ это может сильно усложнить эксперимент.

Выражение (1.26) является статистическим определением среднего времени безотказной работы.

Среднее время безотказной работы является одной из наиболее наглядных количественных характеристик надежности. Однако этой характеристике надежности свойственны существенные недостатки. Как математическое ожидание случайной величины, она не может полностью характеризовать время работы аппаратуры. Необходимо еще знать, по меньшей мере, дисперсию времени отказов аппаратуры. Кроме того, T фактически не позволяет оценить надежность аппаратуры, время работы которой во много раз меньше среднего времени безотказной работы.

Из выражения (1.26) видно, что для вычисления T определяются времена отказов каждого из N₀ образцов. В дальнейшем они в эксперименте не участвуют. Таким образом, среднее время безотказной работы характеризует надежность аппаратуры до первого отказа. Это означает, что T хорошо характеризует надежность аппаратуры разового использования, например, простейших элементов, которые после отказа не ремонтируются.

Величину T можно использовать и для оценки надежности сложных устройств. Однако в этом случае T характеризует надежность до первого их отказа.

У аппаратуры длительного использования, работающей в режиме смены отказавших элементов, среднее время безотказной работы до первого отказа может существенно отличаться от среднего времени между первым и вторым отказами, вторым и третьим и т.д. Это означает, что среднее время безотказной работы может характеризовать надежность такой аппаратуры только до первого отказа.

Поэтому надежность аппаратуры длительного использования оценивают, в отличие от среднего времени безотказной работы, так называемой наработкой на отказ.

Этой характеристике дают следующее определение: наработкой на отказ называется среднее значение времени между соседними отказами, при условии восстановления каждого отказавшего элемента.

Эта характеристика обозначается t_ср и определяется из статистических данных об отказах по формуле:

,                                                      (1.27)

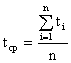
где t_i – время исправной работы аппаратуры между (i – 1)-м и i-м отказами; n – число отказов аппаратуры за время t.

Из определения и формулы (1.27) видно, что наработка на отказ является средним временем между соседними отказами. Формулой (1.27) удобно пользоваться, если t_ср определяется по данным об отказах лишь одного образца аппаратуры. Если испытание проводится с несколькими образцами, то t_ср вычисляется по формуле:

                                                   (1.28)

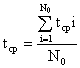
где t_ср._i — среднее время между соседними отказами i-го образца, вычисленное по формуле (1.27), N₀ – число испытываемых образцов.

Найти связь среднего времени между соседними отказами с другими количественными характеристиками надежности проще всего через среднюю частоту отказов. Действительно, если известны средние частоты отказов элементов сложной системы, то среднее число отказов системы в любом промежутке времени определяется ее суммарной частотой отказов. Тогда среднее время между соседними отказами будет равно величие, обратной суммарной частоте отказов, т.е.

                                                    (1.29)

или

,                                               (1.30)

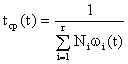
где r – число типов элементов.

Вероятность безотказной работы P(t), частота отказов α(t) (средняя частота отказов ), интенсивность отказов  и среднее время безотказной работы T (среднее время между соседними отказами t_ср) являются основными количественными характеристиками надежности. Каждая из них имеет свои достоинства и недостатки. Ни одна из них не является исчерпывающей характеристикой надежности. Только все они в совокупности во многих случаях могут характеризовать достаточно полно надежность аппаратуры в течение времени ее работы.

Плотность
распределения времени безотказной
работы f(t)
— это плотность распределения случайной
величины Т. Она наиболее полно характеризует
Надежность техники в данный момент
(точечная характеристика). По ней можно
определить любой показатель надежности
невосстанавливаемой системы. В этом
состоит достоинство плотности
распределения времени безотказной
работы.

Производная
от вероятности отказа по времени есть
плотность
вероятности, или дифференциальный закон
распределения времени работы объекта
до отказа, т.е.

(5)

Полученная
математическая связь позволяет записать:

;
(6)

Таким
образом, зная плотность вероятности
f(t),
легко найти искомую величину P(t) и Q(t).

Соотношения
(6) имеют место при любом законе
распределения времени возникновения
отказов.

Достоинством
является следующее. Как плотность
распределения вероятности, она наиболее
полно характеризует случайное время
возникновения отказов и по ней легко
определить вероятность безотказной
работы, математическое ожидание,
дисперсию и другие удобные характеристики
распределения.

К
недостаткам плотности
вероятности f(t)
следует отнести то, что она характеризует
надежность аппаратуры до первого отказа.
Оценить с помощью частоты отказа
надежность аппаратуры длительного
пользования, которая может ремонтироваться,
затруднительно. В общем случае надежность
аппаратуры длительного пользования
обычно характеризуется средней частотой
отказа.

Под
частотой отказов элементов понимают
отношение числа отказавших образцов
техники в единицу времени к числу
испытуемых образцов при условии, что
отказавшие образцы не восполняются
исправными:

,
(7)

где
n(t, t+∆t)
– число отказавших образцов за промежуток
времени (t, t+∆t);
N₀ – число образцов,
первоначально поставленных на испытания;
∆t – длина промежутка
времени.

Так как число
отказавших образцов в интервале времени


 может
зависеть от расположения этого промежутка
по оси времени, то частота отказов
является функцией времени t.

Соотношение
(7) следует из того, что f(t)=Q’(t)=–P’(t),
а для малых значений ∆t

.

Если
N(t) – число
исправных образцов к моменту времени
t, а N(t+
∆t) — число исправных
образцов к моменту времени t+∆t,
то

На
практике достаточно часто приходится
определять условную вероятность
безотказной работы объекта в заданном
интервале времени Р(t₁,t₂)
при условии, что в момент времени t₁
объект работоспособен и известны Р (t₁)
и Р (t₂).
По формуле вероятности совместного
появления двух зависимых событий

,

откуда

(*)

По
известным статистическим данным можно
записать:

(**)

где
N(t₁),
N(t₂)
— число объектов, работоспособных
соответственно к моментам времени t₁
и t_2, т.е.
N(t₁)=N₀
— n(t₁);
N(t₂)=N₀
— n(t₂).

3. Среднее время безотказной работы (средняя наработка до отказа)

Средним
временем безотказной работы
(средней наработкой
до отказа) T₁
называется
математическое ожидание времени
безотказной работы технического объекта
(наработки объекта до первого отказа):

T₁=M(T).

Как математическое ожидание
случайной величины с плотностью f(t),
среднее время безотказной работы
вычисляется по формуле:

Используя
известную связь между f(t), Q(t) и P(t), запишем:

Интегрируя
по частям, получим:

Учитывая,
что Р(0) = 1, P(+)=0,
полагая, что

,
получим:

.
(8)

Таким
образом, средняя наработка до отказа
равна площади, образованной кривой
вероятности безотказной работы P(t) и
осями координат.

Среднее
время безотказной работы является
интегральным показателем надежности.
Его основное достоинство — высокая
наглядность. Недостаток этого
показателя в том, что он, будучи
интегральным, характеризует надежность
техники длительного времени работы.

По
статистическим данным об отказах T₁
определяется по формуле:

(9)

где N_o
— число испытуемых образцов техники (в
начале испытания); t_j
– время безотказной работы j-го образца.

Из выражения
(9) видно, что для определения среднего
времени безотказной работы необходимо
знать времена отказов всех образцов,
над которыми производятся испытания.
Поэтому при большом числе образцов
предпочитают пользоваться формулой

 
    
                                            

(10)

где n_i(t)
— число образцов, отказавших в i -том
интервале;

—
среднее время i-го интервала (
);
     

t_k—
время, в течение которого отказали все
N₀ образцов;

t
— выбранная величина интервала времени.

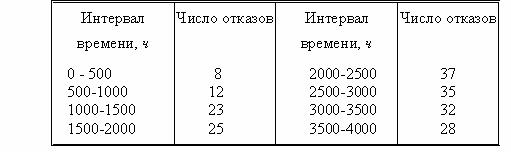
Пример. В
процессе эксплуатации приборов одного
типа учитывалось число вышедших  из
строя приборов в течении каждых 500 часов
работы, при этом наблюдение велось за
200 одинаковыми приборами (
=200).
в результате подсчета отказавших
приборов получены данные, сведенные в
табл.1.

По данным табл.1,
пользуясь формулой (2), определим
вероятность безотказной работы прибора
к любому моменту времени:

Таблица 1.

Количество
отказов приборов в i-ом интервале времени

Воспользовавшись
формулой (4), определим вероятность
отказа приборов, например, для тех же
моментов времени:

Определим также
среднюю наработку до отказа приборов
по формуле (10):

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

---

Различают вероятностные (математические) и статистические показатели надежности. Математические показатели надежности выводятся из теоретических функций распределения вероятностей отказов. Статистические показатели надежности определяются опытным путем при испытаниях объектов на базе статистических данных эксплуатации оборудования.

Надежность является функцией многих факторов, большинство из которых случайны. Отсюда ясно, что для оценки надежности объекта необходимо большое количество критериев.

Критерий надежности – это признак, по которому оценивается надежность объекта.

Критерии и характеристики надежности носят вероятностный характер, поскольку факторы, влияющие на объект, носят случайный характер и требуют статистической оценки.

Количественными характеристиками надежности могут быть:
• вероятность безотказной работы;
• среднее время безотказной работы;
• интенсивность отказов;
• частота отказов;
• различные коэффициенты надежности.

1. Вероятность безотказной работы

Служит одним из основных показателей при расчетах на надежность.
Вероятность безотказной работы объекта называется вероятность того, что он будет сохранять свои параметры в заданных пределах в течение определенного промежутка времени при определенных условиях эксплуатации.

В дальнейшем полагаем, что эксплуатация объекта происходит непрерывно, продолжительность эксплуатации объекта выражена в единицах времени t и эксплуатация начата в момент времени t=0.
Обозначим P(t) вероятность безотказной работы объекта на отрезке времени [0,t]. Вероятность, рассматриваемую как функцию верхней границы отрезка времени, называют также функцией надежности.
Вероятностная оценка: P(t) = 1 – Q(t), где Q(t) — вероятность отказа.

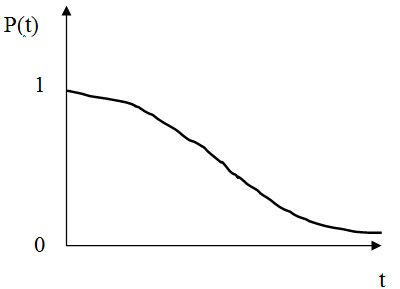
Типичная кривая вероятности безотказной работы

Из графика очевидно, что:
1. P(t) – невозрастающая функция времени;
2. 0 ≤ P(t) ≤ 1;
3. P(0)=1; P(∞)=0.

На практике иногда более удобной характеристикой является вероятность неисправной работы объекта или вероятность отказа:
Q(t) = 1 – P(t).
Статистическая характеристика вероятности отказов: Q*(t) = n(t)/N

2. Частота отказов

Частотой отказов называется отношение числа отказавших объектов к их общему числу перед началом испытания при условии что отказавшие объекты не ремонтируются и не заменяются новыми, т.е

a*(t) = n(t)/(NΔt)
где a*(t) — частота отказов;
n(t) – число отказавших объектов в интервале времени от t – t/2 до t+ t/2;
Δt – интервал времени;
N – число объектов, участвующих в испытании.

Частота отказов есть плотность распределения времени работы изделия до его отказа. Вероятностное определение частоты отказов a(t) = -P(t) или a(t) = Q(t).

Таким образом, между частотой отказов, вероятностью безотказной работы и вероятностью отказов при любом законе распределения времени отказов существует однозначная зависимость: Q(t) = ∫ a(t)dt.

Отказ трактуют в теории надежности как случайное событие. В основе теории лежит статистическое истолкование вероятности. Элементы и образованные из них системы рассматривают как массовые объекты, принадлежащие одной генеральной совокупности и работающие в статистически однородных условиях. Когда говорят об объекте, то в сущности имеют в виду наугад взятый объект из генеральной совокупности, представительную выборку из этой совокупности, а часто и всю генеральную совокупность.

Для массовых объектов статистическую оценку вероятности безотказной работы P(t) можно получить, обработав результаты испытаний на надежность достаточно больших выборок. Способ вычисления оценки зависит от плана испытаний.

Пусть испытания выборки из N объектов проведены без замен и восстановлений до отказа последнего объекта. Обозначим продолжительности времени до отказа каждого из объектов t₁, …, t_N. Тогда статистическая оценка:

P*(t) = 1 — 1/N ∑η(t-t_k)

где η — единичная функция Хевисайда.

Для вероятности безотказной работы на определенном отрезке [0, t] удобна оценка P*(t) = [N — n(t)]/N,
где n(t) – число объектов, отказавших к моменту времени t.

Частота отказов, определяемая при условии замены отказавших изделий исправными, иногда называется средней частотой отказов и обозначается ω(t).

3. Интенсивность отказов

Интенсивностью отказов λ(t) называется отношение числа отказавших объектов в единицу времени к среднему числу объектов, работающих в данный отрезок времени, при условии, что отказавшие объекты не восстанавливаются и не заменяются исправными: λ(t) = n(t)/[N_срΔt]
где N_ср = [N_i + N_i+1]/2 — среднее число объектов, исправно работавших в интервале времени Δt;
N_i – число изделий, работавших в начале интервала Δt;
N_i+1 – число объектов, исправно работавших в конце интервала времени Δt.

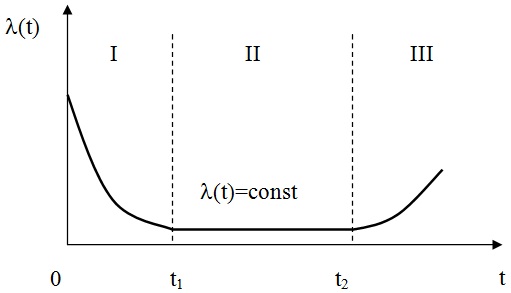
Ресурсные испытания и наблюдения над большими выборками объектов показывают, что в большинстве случаев интенсивность отказов изменяется во времени немонотонно.

Типичная кривая изменения интенсивности отказов объекта

Из кривой зависимости отказов от времени видно, что весь период работы объекта можно условно поделить на 3 периода.
I — й период – приработка.

Приработочные отказы являются, как правило, результатом наличия у объекта дефектов и дефектных элементов, надежность которых значительно ниже требуемого уровня. При увеличении числа элементов в изделии даже при самом строгом контроле не удается полностью исключить возможность попадания в сборку элементов, имеющих те или иные скрытые дефекты. Кроме того, к отказам в этот период могут приводить и ошибки при сборке и монтаже, а также недостаточная освоенность объекта обслуживающим персоналом.

Физическая природа таких отказов носит случайный характер и отличается от внезапных отказов нормального периода эксплуатации тем, что здесь отказы могут иметь место не при повышенных, а и при незначительных нагрузках («выжигание дефектных элементов»).
Снижение величины интенсивности отказов объекта в целом, при постоянном значении этого параметра для каждого из элементов в отдельности, как раз и объясняется «выжиганием» слабых звеньев и их заменой наиболее надежными. Чем круче кривая на этом участке, тем лучше: меньше дефектных элементов останется в изделии за короткий срок.

Чтобы повысить надежность объекта, учитывая возможность приработочных отказов, нужно:
• проводить более строгую отбраковку элементов;
• проводить испытания объекта на режимах близких к эксплуатационным и использовать при сборке только элементы, прошедшие испытания;
• повысить качество сборки и монтажа.

Среднее время приработки определяют при испытаниях. Для особо важных случаев необходимо увеличить срок приработки в несколько раз по сравнению со средним.

II — й период – нормальная эксплуатация
Этот период характеризуется тем, что приработочные отказы уже закончились, а отказы, связанные с износом, еще не наступили. Этот период характеризуется исключительно внезапными отказами нормальных элементов, наработка на отказ которых очень велика.

Сохранение уровня интенсивности отказов на этом этапе характеризуется тем, что отказавший элемент заменяется таким же, с той же вероятностью отказа, а не лучшим, как это происходило на этапе приработки.

Отбраковка и предварительная обкатка элементов, идущих на замену отказавших, имеет для этого этапа еще большее значение.
Наибольшими возможностями в решении этой задачи обладает конструктор. Нередко изменение конструкции или облегчение режимов работы всего одного-двух элементов обеспечивает резкое повышение надежности всего объекта. Второй путь – повышение качества производства и даже чистоты производства и эксплуатации.

III – й период – износ
Период нормальной эксплуатации заканчивается, когда начинают возникать износовые отказы. Наступает третий период в жизни изделия – период износа.

Вероятность возникновения отказов из-за износов с приближением к сроку службы возрастает.

С вероятностной точки зрения отказ системы в данном промежутке времени Δt = t₂ – t₁ определяется как вероятность отказа:

∫a(t) = Q₂(t) — Q₁(t)

Интенсивность отказов есть условная вероятность того, что в промежуток времени Δt произойдет отказ при условии, что до этого он не произошел λ(t) = [Q₂ — Q₁]/[ΔtP(t)]
λ(t) = lim [Q₂ — Q₁]/[ΔtP(t)] = [dQ(t)]/[P(t)dt] = Q'(t)/P(t) = -P'(t)/P(t)
так как a(t) = -P'(t), то λ(t) = a(t)/P(t).

Эти выражения устанавливают зависимость между вероятностью безотказной работы, частотой и интенсивностью отказов. Если a(t) – невозрастающая функция, то справедливо соотношение:
ω(t) ≥ λ(t) ≥ a(t).

4. Среднее время безотказной работы

Средним временем безотказной работы называется математическое ожидание времени безотказной работы.

Вероятностное определение: среднее время безотказной работы равно площади под кривой вероятности безотказной работы.

T = ∫P(t)dt

Статистическое определение: T* = ∑θ_i/N₀
где θ_I – время работы i-го объекта до отказа;
N₀ – начальное число объектов.

Очевидно, что параметр Т* не может полностью и удовлетворительно характеризовать надежность систем длительного пользования, так как является характеристикой надежности только до первого отказа. Поэтому надежность систем длительного использования характеризуют средним временем между двумя соседними отказами или наработкой на отказ t_ср:
t_ср = ∑θ_i/n = 1/ω(t),
где n – число отказов за время t;
θ_i – время работы объекта между (i-1)-м и i-м отказами.

Наработка на отказ – среднее значение времени между соседними отказами при условии восстановления отказавшего элемента.