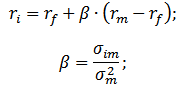На чтение 8 мин Просмотров 65.6к.
Рассмотрим практические аспекты построения модели оценки капитальных активов CAPM с помощью Excel для отечественных акций ОАО «Газпром».
Модель оценки капитальных активов (англ. Capital Assets Price Model, CAPM) – модель оценки (прогнозирования) будущей доходности актива для инвесторов. Подход оценки активов был теоретически разработана еще в 50-е годы Г.Марковицем, и окончательно сформирован в виде модели в 60-е годы У.Шарпом (1964), Дж. Трейнором (1962), Дж. Линтнером (1965), Ж. Мосином (1966).
★ Инвестиционная оценка в Excel. Расчет NPV, IRR, DPP, PI за 5 минут
Модель CAPM основывается на гипотезе эффективного рынка капитала (Efficient Market Hypothesis, EMH), созданной еще в начале 20-го века Л. Башелье и активно продвигаемую Ю.Фамой в 60-е годы. Данная гипотеза имеет ряд условий по способу распространению информации и действию инвесторов на эффективном рынке капитала:
- Информация свободно распространяется и доступно всем инвесторам, рынок имеет совершенную конкуренцию. Другими словами, отсутствуют инсайдеры, которые обладают большим преимуществом в принятии решений и получении сверхдоходности (выше среднерыночной).
- Любое изменение информации о компании сразу приводит к изменению стоимости ее активов (акций). Это исключает возможность использования любой активной стратегии инвестирования для получения сверхприбыли. Данная предпосылка исключает возможность арбитражных сделок, когда инвестор заранее имеет полезную информацию, тогда как цена на активы компании еще не изменилась.
- Инвесторы на эффективном рынке имеют долгосрочный горизонт вложения. Это исключает возникновение резких изменений цен на активы (акции) и кризисов.
- Активы имеют высокую ликвидность и абсолютно делимы.
Исходя из гипотезы эффективного рынка, У. Шарп сделал предположение, что на будущую доходность акции будут оказывать влияние только рыночные (системные) риски. Другими словами, будущую доходность акции будут определять общее настроение рынка. Поэтому, кстати, он и был сторонником пассивного инвестирования, когда инвестиционный портфель не пересматривается от получения новой информации. Следует отметить, что на эффективном рынке невозможно получить сверхприбыль. Это делает любое активное управление инвестициями (инвестиционным портфелем) не целесообразным и ставит под сомнение эффективность вложения в ПИФы. В результате, модель У. Шарпа имеет всего один фактор – рыночный риск (коэффициент бета). Анализируя данные постулаты эффективного рынка, можно заметить, что в современной экономике многие из них не выполняются. Модель CAPM в большей степени является теоретической моделью и может использоваться на практике в общем случае.
Содержание
- Модель CAPM. Формула расчета
- Расчет модели CAPM в Excel
- Расчет коэффициента бета с помощью формул Excel
- Расчет коэффициента бета через надстройку «Регрессия»
- Что показывает коэффициент бета в модели CAPM?
- Расчет безриковой ставки для модели CAPM
- Расчет средней доходности рынка
- Расчет будущей доходности по модели CAPM
- Преимущества и недостатки модели CAPM
Модель CAPM. Формула расчета
Формула оценки будущей доходности актива (акции) по модели CAPM имеет следующий аналитический вид:
где:
r – ожидаемая доходность актива (акций);
rf – доходность по безрисковому активу;
rm – среднерыночная доходность;
β – коэффициент бета (мера рыночного риска), который отражает чувствительность изменения стоимости активов в зависимости от доходности рынка. Данный коэффициент иногда называют коэффициент Шарпа.
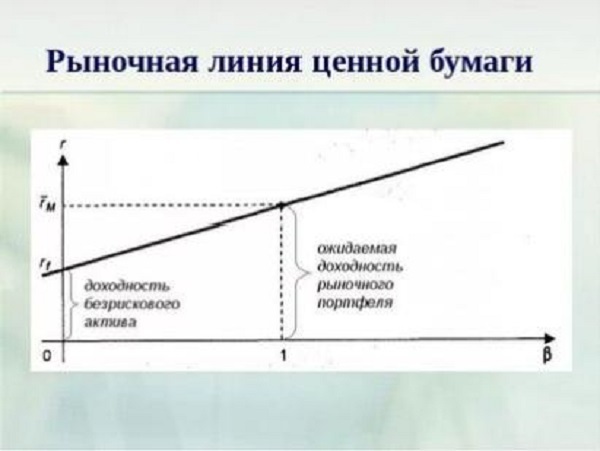
Модель представляет собой уравнение линейной регрессии и показывает линейную взаимосвязь между доходностью (r) и рыночным риском (β);
σim – стандартное отклонение изменения доходности акции от изменения доходности рынка;
σ2m – дисперсия рыночной доходности.
Расчет модели CAPM в Excel
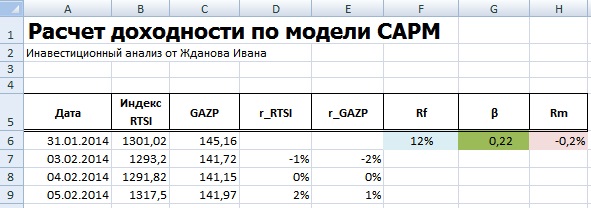
Для того чтобы лучше понять модель CAPM разберем ее на реальном примере акций предприятия ОАО «Газпром». Для этого воспользуемся программой Excel. Получить котировки акций можно на сайте finam.ru в разделе «Про рынок» → «Экспорт данных».
В нашей формуле за рыночную доходность будем брать изменения индекса РТС (RTSI), также это может быть индекс ММВБ (MICECX). Для американских акций зачастую берут изменения индекса S&P500. Были взяты ежедневные котировки акции и индекса за 1 год (250 данных), начиная с 31.01.2014 по 30.01.2015 г.
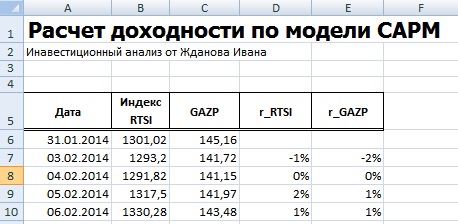
Далее необходимо рассчитать доходности акции (E) и индекса (D), по формулам:
=(B7-B6)/B6
=(C7-C6)/C6
Хочется заметить, что для оценки доходностей могла быть использована также формула расчета через натуральный логарифм:
=LN(B7/B6)
=LN(C7/C6)
Итоговый результат расчета доходности одинаковый.
На следующем этапе необходимо рассчитать значение коэффициента бета, отражающего рыночный риск акции. Для этого есть два варианта расчета.
Расчет коэффициента бета с помощью формул Excel
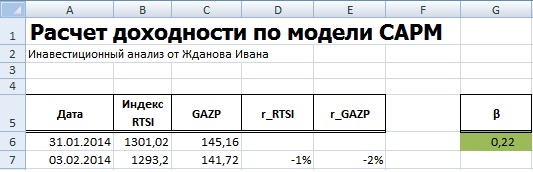
Для расчета коэффициента бета можно воспользоваться формулой ИНДЕКС и ЛИНЕЙН, первая позволяет взять индекс b из формулы линейной регрессии между доходностями акции и индекса, который соответствует коэффициенту бета. Формула расчета будет следующая:
=ИНДЕКС(ЛИНЕЙН(E7:E256;D7:D256);1)
Расчет коэффициента бета через надстройку «Регрессия»
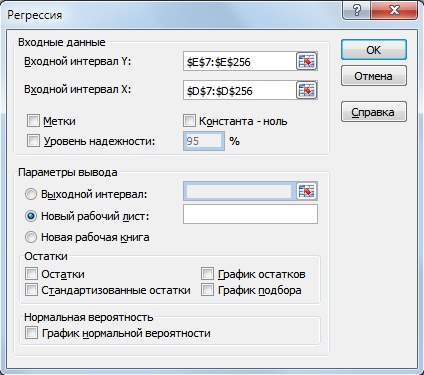
Второй вариант расчета рыночного риска модели заключается в использовании надстройки в разделе «Главное меню» → «Данные» →«Анализ данных» → «Регрессия».
В открывшемся окне необходимо заполнить два поля: «Входной интервал Y» и «Входной интервал Х» доходностями индекса и акции соответственно.
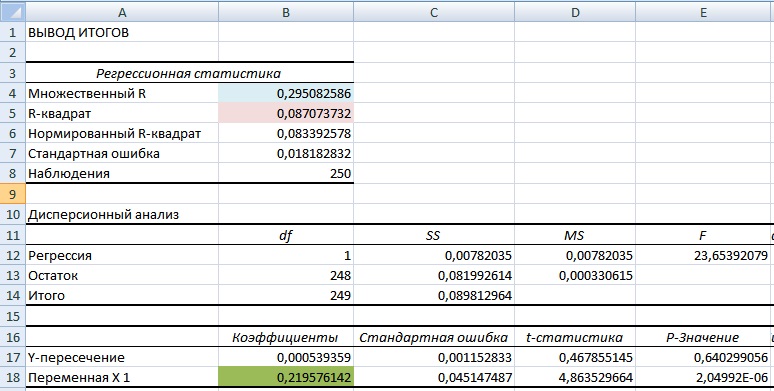
На новом листе Excel появится основные параметры модели линейной регрессии. В ячейке В18 отразится рассчитанный коэффициент линейной регрессии – коэффициент бета. Рассмотрим другие полученные параметры анализа. Так показатель Множественной R (коэффициента корреляции) между доходностью акции и индекса составляет 0,29, что показывает низкую степень зависимости доходности акции от доходности индекса. Коэффициент R-квадрат (коэффициент детерминированности) отражает точность полученной модели. Точность составляет 0,08, что очень мало для того чтобы принимать адекватные решения о прогнозировании будущей доходности на основе взаимосвязи только с уровнем риска рынка.
Что показывает коэффициент бета в модели CAPM?
Коэффициент бета показывает чувствительность изменения доходности акции и доходности рынка. Другими словами, отражает рискованность вложения в тот или иной актив. Коэффициент бета служит мерой рыночного риска. Знак перед показателем отражает их однонаправленное или разнонаправленное движение. Рассмотрим более подробно значение бета в таблице ниже:
| Значение коэффициента бета | Комментарии |
| β > 1 | Доходность акция более чувствительная к изменению, доходности рынка |
| β = 1 | Доходность акции совпадает доходности рынка |
| 0 < β < 1 | Доходность акции менее чувствительна к изменениям доходности рынка |
| β = 0 | Доходность акции не зависит от доходности рынка полностью |
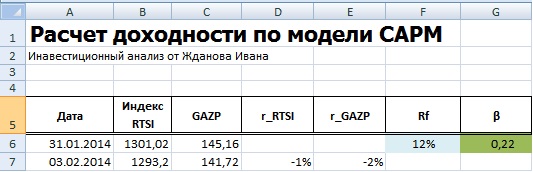
В нашем примере, мы получили значение бета равной 0,22 – это показывает малую степень влияния рыночного риска на доходность акции ОАО «Газпром». На следующем этапе необходимо рассчитать безрисковую ставку (rf).
Расчет безриковой ставки для модели CAPM
Безрисковая ставка представляет собой гарантированный уровень доходности, который получил бы инвестор при осуществлении альтернативного инвестирования. На практике за безрисковую процентную ставку берут процентные ставки государственных ценных бумаг (ГКО – государственные краткосрочные бескупонные облигации, ОФЗ – облигации федерального займа ) и (доходность 30-летних облигаций США). Доходности по российским ценным бумагам можно посмотреть на сайте ЦБ РФ «Ставки рынка ГКО-ОФЗ». На текущий момент, процентная ставка составляет около 12% годовых. Отразим полученные данные в таблице Excel.
Расчет средней доходности рынка
Расчет средней доходности рынка (индекса РТС) проходит простой формуле Excel:
=СРЗНАЧ(D6:D256)
Расчет будущей доходности по модели CAPM
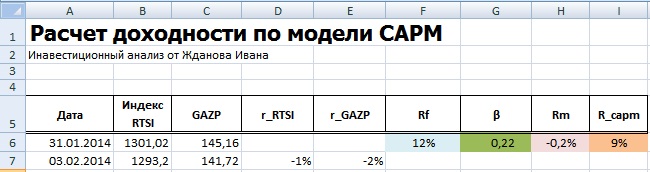
Рассчитаем будущую доходность акции ОАО «Газпром» на основе модели CAPM (R_capm). Формула оценки следующая:
=F6+G6*(H6-F6)
Как мы видим, что по модели CAPM ожидается доходность акции ОАО «Газпром» в размере 9%, что ниже, чем доходность по безрисковому активу. Доходность рынка составила отрицательное значение (-0,2%). Это объясняется тем, что сейчас наблюдается кризис на фондовом рынке, что приводит к оттоку капитала и созданию неустойчивой инвестиционной среды. Современные методы оценки инвестиций и инвестиционных портфелей вы можете прочитать в моей статье: «Оценка эффективности инвестиций, инвестиционного портфеля, акций на примере в Excel«.
Преимущества и недостатки модели CAPM
К преимуществам модели можно отнести ее фундаментальный принцип о взаимосвязи между уровнем рыночного риска (системного риска) и уровнем будущей доходности акции.
Рассмотрим недостатки модели CAPM.
Во-первых, модель оперирует только одним фактором, влияющим на будущую доходность акции. В 1992 году Ю. Фама К. Френч доказали, что на будущую доходность также влияют такие факторы как: размер компании и отраслевая принадлежность.
Во-вторых, модель имеет ряд ограничений: модель не учитывает налоги, трансакционные затраты, непрозрачность финансового рынка и т.д.
В-третьих, для прогнозирования будущей доходности используют ретроспективный уровень рыночного риска, что приводит к ошибке прогноза.
Резюме
В данной статье мы рассмотрели на практическом примере расчет будущей доходности акции ОАО «Газпром» в Excel. Следует отметить, что модель CAPM может применяться в условиях эффективного рынка капитала. В настоящее время увеличивается количество кризисов на финансовых рынках, это делает затруднительным использование модели в долгосрочной оценки активов. Несмотря на это, модель может быть использована как метод анализа силы влияния рыночного риска на будущую доходность акции. Спасибо за внимание, с вами был Иван Жданов.
Автор: к.э.н. Жданов Иван Юрьевич
На чтение 8 мин Просмотров 2.6к.
Обновлено 27.03.2021
Содержание
- Что такое модель CAPM
- Для чего необходима модель оценки капитальных активов
- Формула расчета
- Расчет модели CAPM в Excel
- Как устроена модель CAPM
- Как можно использовать модель CAPM
- Где применяется модель CAPM
- Преимущества и недостатки модели CAPM
- Пример расчета
- Заключение
CAPM (Capital Asset Pricing Model) – одна из методик оценки стоимости активов акционерного общества с точки зрения рисков, присущих как непосредственно оцениваемому активу, так и рынку в целом.
Модель CAPM построена на предположении: инвесторы заинтересованы в получении дохода выше, чем доход по безрисковым активам.
CAPM – это метод, который может применяться в теории, на практике его использование возможно лишь в некоторых случаях, в комбинации с другими методиками.
Сегодня мы рассмотрим модель оценки капитальных активов CAPM: формулу расчета этого показателя, его применение на практике, преимущества и недостатки.
Что такое модель CAPM
Как известно, стоимость акционерного общества определяется стоимостью его активов. В данном случае под активами понимают не основные фонды, а финансовые инструменты, эмитентом которых является предприятие.
Предпосылкой CAPM стала гипотеза эффективного рынка капитала, появившаяся в начале XX века. Эта гипотеза основана на том, что рынок является прозрачным, и любые изменения быстро отражаются на стоимости акций. В целом рынок «заточен» на долгосрочные инвестиции.
Современная модель оценки капитальных активов была разработана в середине XX века американским экономистом Гарри Марковицем. Далее метод CAPM был взят на вооружение другими финансовыми гуру: Джоном Линтнером, Джеком Л. Трейнором и Уильямом Шарпом. Последний в 1964 г. разработал модификацию модели, которая используется по сей день. Иногда модель капитальных активов CAPM называют моделью Шарпа.
Итак, на чем основана CAPM model? Попытаемся объяснить простыми словами.
Предположим, есть некий безрисковый актив с минимальной доходностью и практически нулевой волатильностью. Безрисковым средством в модели CAPM обычно выступают государственные облигации. Помимо этого, в портфеле мы имеем акции предприятия нефтедобывающего комплекса. Эти бумаги могут принести неплохой доход, однако уж очень зависят от внешней ситуации, в том числе политической. Какова цель инвестора? Как сбалансировать портфель?
Если наш инвестор очень осторожен, то в его портфеле будут преобладать ОФЗ. Да, он не получит высокий доход, но и ничего не потеряет. А если он все-таки хочет, чтобы его деньги работали и приносили прибыль, то он будет двигаться в сторону увеличения доли бумаг с высокой волатильностью. При этом должно соблюдаться общее правило: если эти бумаги начнут падать и приносить убыток, общая должность портфеля не должна быть ниже, чем ставка доходности по ОФЗ.
Для чего необходима модель оценки капитальных активов
Итак, на чем основана модель оценки капитальных активов? Инвестор должен представлять, какой доход он может получить за то, что рискует своими деньгами.
Наглядно CAPM представлена на графике:
Модель CAPM описывает зависимость между доходностью актива, ставкой по безрисковым инструментам и рыночному риску в целом.
CAPM включает элементы:
- доходность безрискового актива;
- ожидаемая общая доходность портфеля;
- общая рыночная доходность;
- чувствительность инструмента к колебаниям рынка (коэффициент β).
Итак, CAPM применяется для оценки доходности ценной бумаги или проекта с учетом систематического (недиверсифицируемого) риска.
Недиверсифицируемый риск – это риск, связанный с отсутствием стабильности в получении дохода. Так, в одном году доходность может быть максимальная, а в следующем периоде оказаться нулевой. Подобные риски присущи ценным бумагам российских компаний, в т.ч. «голубым фишкам».
Возникает резонный вопрос: как рассчитывать или где взять значение коэффициента β? Этот показатель берется из данных статистики. Можно рассчитать коэффициент самостоятельно, используя функции линейной регрессии в Excel, что мы и сделаем в примере ниже. Для этого нужны данные доходности за определенный период по анализируемому активу и в целом по рынку. Для российских бумаг обычно используются индексы РТС или ММВБ, для зарубежных – S&P 500, NASDAQ и др.
Поскольку значения индекса основаны на данных за предыдущие периоды, а само понятие систематического риска говорит о непредсказуемости изменения цены и доходности инструмента, применять расчеты на практике следует с осторожностью. Тем не менее рассчитаем Capital Asset Pricing Model по формуле и в Excel, используя данные по котировкам, находящиеся в свободном доступе.
Формула расчета
Формула CAPM выглядит так:
[ RE=Rf + β*(Rm – Rf), где: ]
( RE ) – ожидаемая ставка;
( Rf )– ставка по безрисковым инструментам;
( Rm ) – усредненная прибыль по портфелю в целом;
( β ) – коэффициент чувствительности актива к колебаниям рынка.
Например, средняя ставка по ОФЗ – 4%. Ожидаемая доходность по портфелю – 20%. Коэффициент β – 0,5.
Приведем таблицу значений β:
| Значение | Комментарий |
|---|---|
| β > 1 | Инструмент чувствителен к колебаниям рынка |
| β = 1 | Доходность актива равна доходности по рынку |
| 0 < β < 1 | Рыночные колебания влияют на цену, но в незначительной степени |
| β < 0 | Цена не зависит от рыночной ситуации |
Итак, в нашем случае цена зависит от рыночной доходности, но в малой степени.
Рассчитаем ожидаемую ставку по CAPM:
[ RE=4 + 0.5 х (20 – 4)=12%. ]
Таким образом, инвестор ожидает, что инструмент будет приносить доход в размере 12%.
Расчет модели CAPM в Excel
Приведем пример расчета модели CAMP с использованием редактора Excel. Исходные данные будут такие:
- анализируемый инструмент – акции Tesla;
- рыночная доходность определяется по индексу NASDAQ;
- безрисковый актив – 30-летние облигации США, средняя ставка доходности по ним в 2020 году – 1,51%.
| Месяц | NASDAQ | TSLA | r_NASDAQ | r_TSLA | Rf | β | Rm | RE (formula CAMP) |
|---|---|---|---|---|---|---|---|---|
| Янв. ’20 | 9 150,94 | 130,11 | 1,51% | 3,17 | 3,46% | 7,69% | ||
| Февр. ’20 | 8 567,37 | 133,60 | -6% | 3% | ||||
| Март ’20 | 7 700,10 | 104,80 | -10% | -22% | ||||
| Апр. ’20 | 8 889,55 | 156,38 | 15% | 49% | ||||
| Май ’20 | 9 489,87 | 167,00 | 7% | 7% | ||||
| Июнь ’20 | 10 058,76 | 215,96 | 6% | 29% | ||||
| Июль ’20 | 10 745,27 | 286,15 | 7% | 33% | ||||
| Авг. ’20 | 11 775,46 | 498,32 | 10% | 74% | ||||
| Сент. ’20 | 11 167,51 | 429,01 | -5% | -14% | ||||
| Окт. ’20 | 10 911,59 | 388,04 | -2% | -10% | ||||
| Нояб. ’20 | 12 198,74 | 567,60 | 12% | 46% | ||||
| Дек. ’20 | 12 888,28 | 705,67 | 6% | 24% |
Коэффициент β посчитан способом линейной регрессии между доходностями по акциям Tesla и индексу NASDAQ и составляет 3,17. Как мы помним, значение больше единицы указывает на то, что акции чувствительны к изменению рыночной доходности.
[ RE=Rf + β х (Rm – Rf)=1,51% + 3,17 х (3,46% – 1,51%)=7,69%. ]
Ожидаемая доходность выше ставки по безрисковым бумагам и значительно выше рыночной доходности Rm, которая рассчитана как среднее значение по индексу NASDAQ.
Как устроена модель CAPM
Модель ценообразования на капитальные активы предполагает следующее:
- Инвестор, который желает увеличить доходность, будет сокращать долю безрискового инструмента в своем портфеле до минимума.
- Структура рынка постоянно является оптимальной: на каждую единицу риска всегда приходится единица рыночной премии (разница между Rm и Rf).
- Коэффициент β отражает зависимость цены на акцию от колебаний рынка.
- Если доходность инструмента ниже значения RE, рассчитанного по модели оценки CAPM, то приобретать данный инструмент смысла не имеет.
Как можно использовать модель CAPM
Базовая модель оценки капитальных активов соответствует критерию определения цены капитала: сумма ожидаемой прибыли деленная на количество ценных бумаг.
Ожидаемая доходность рассчитывается с учетом рисков и чувствительности цены к изменениям общей ситуации на рынке. Модель CAPM исходит из того, что инвесторы могут варьировать структуру портфеля с учетом премии за риск. В свою очередь, финансовые менеджеры используют модель для расчета стоимости капитала компании.
Где применяется модель CAPM
Итак, основные задачи CAPM – определение цены капитала и премии за риск. В связи с этим модель можно использовать при расчете ставки дисконтирования. Области применения могут быть самые разные.
Так, аналитики рассчитывают стоимость капитала по компании, ее подразделениям, фирмам-конкурентам и отрасли в целом. Инвестор, сравнивая ожидаемую прибыль с доходностью по безрисковым инструментам, принимает решение об увеличении или сокращении доли того или иного актива в портфеле.
Преимущества и недостатки модели CAPM
Перечислим плюсы использования модели:
- Базовая модель оценки капитальных активов соответствует основному принципу рынка: чем выше риск, тем больше потенциальная прибыль.
- Коэффициент бета является одним из важных показателей, характеризующих систематический риск. Несмотря на то, что эта величина рассчитывается несколько сложно (при помощи математических функций), ее отсутствие в других методиках дает менее точные результаты.
- Модель CAPM можно использовать для расчета ставки дисконтирования.
Недостатки модели оценки капитальных активов заключаются в следующем:
- Метод не учитывает несколько важных факторов: отраслевые особенности, налогообложение, размеры компании и др.
- Модель ценообразования капитальных активов строится на основании данных за прошлые периоды, что не исключает вероятность ошибочных прогнозов. В самом деле, мы проанализировали акции Tesla и получили неплохой результат. А как долго можно на него ориентироваться, учитывая включение компании в другие индексы, например S&P 500? На этот вопрос вряд ли можно получить ответ.
- Расчет дает неверные результаты при отрицательной доходности.
Пример расчета
Итак, модель оценки капитальных активов включает следующие компоненты:
- безрисковая ставка дохода (Rf);
- коэффициент β (уровень систематического риска);
- рыночная доходность (Rm).
Рассмотрим простой пример расчета ставки дохода на собственный капитал (RE) по модели CAPM с использованием исходных данных:
( Rf )=5% (ставка по ОФЗ);
( β )=1,5;
( Rm )=12%.
Сначала рассчитаем премию за риск:
12 – 5=7%
[ RE=0,05 + 1,5 х 0,07=0,155 ]
Таким образом, ставка дохода на собственный капитал составляет 15,5%.
Заключение
Базовая модель ценообразования на капитальные активы используется для оценки степени влияния риска на будущую доходность ценных бумаг. Применение CAPM в условиях кризисов может давать недостоверные результаты ввиду высокой волатильности рынка: возникает необходимость постоянно пересчитывать премию за риск, которая меняется практически каждый день. Ориентированная на долгосрочную перспективу, модель CAPM не подходит для такой ситуации.
Как и любой другой инструмент расчета, модель оценки активов CAPM следует использовать в совокупности с другими методиками: WACC (средневзвешенная стоимость капитала), DDM (модель дисконтирования дивидендов) и др.
Модель ценообразования капитальных активов (CAPM) – это модель для оценки ожидаемой доходности актива, основанной исключительно на систематическом риске доходности актива. Логика, по которой оценивается только систематический риск, заключается в том, что в идеально эффективной экономической системе инвесторы должны иметь возможность бесплатно диверсифицировать свой портфель, чтобы они могли полностью устранить несистематический или специфический для фирмы риск. Таким образом, если они могут выбрать инвестирование в диверсифицированный портфель активов, а не в отдельный актив, почему они должны требовать премию за единичный риск? Можно легко утверждать, что финансовый мир далек от совершенства и включает в себя транзакционные издержки, налоги и т. Д. Предположим, что можно применить CAPM для оценки ожидаемой прибыли на обыкновенные акции Apple ( Финансовые концепции: модель ценообразования капитальных активов» (CAPM) ].
Теоретически CAPM выражается как:
Модель предполагает, что ожидаемая доходность актива E (R i ) равна сумме безрисковой доходности и премии за рыночный риск, умноженной на бета, β i, актива i. Бета конкретного актива отражает его систематический риск. Уравнение не содержит никаких несистематических факторов риска. β i – наклон линии регрессии E (R i ) относительно избыточной рыночной доходности E (R M ) -R f. Вот пошаговый метод применения CAPM для оценки ожидаемой доходности Apple. (Дополнительную информацию см. В Бета: Знайте о рисках ).
1:43
1. Выбор прокси для рыночного портфеля
Портфель фондового рынка – это портфель, который включает все активы, торгуемые на рынке.Создание такого портфеля было бы слишком дорогостоящим и трудоемким;следовательно, мы можем использоватьиндекс фондового рынка в качестве прокси для рыночного портфеля. S & P 500 является капитализации взвешенного индексом,состоящим из 500 ведущих большой крышки американских компаний и охватывает около 80% всех обращающегося рынка ценных бумаг, с приблизительной рыночной капитализацией в $ 25 триллионов, которая является суммой рыночных колпачков для всех акций в индекс.1
2. Оценка бета-версии Apple
Мы можем оценить бета-версию акций Apple, сравнив доходность Apple с доходностью S&P 500. Самый простой способ оценить бета-версию – использовать следующую формулу:
βя знак равно Cov(я, M)Вар(M) ог βя знак равно ρя, MσяσM (2) beta_I = frac { text {Cov} (I, M)} { text {Var} (M)} text {или} beta_I = frac { rho_ {I, M} sigma_I} { sigma_M} qquad qquad qquad qquad qquad small {(2)}βяВзаимодействие с другими людьми знак равно Вар (М)
где Cov (I, M) – ковариация Apple (I) и рыночной доходности (S&P 500), Var (M) – дисперсия рынка, ρ I, M – коэффициент корреляции между доходностью S&P 500 и акций Apple., σI и σM – стандартные отклонения доходности Apple и рыночной доходности соответственно. Наша отправная точка при оценке бета-версии компании – это оценка ее исторической бета-версии на основе исторических данных о доходности акций. Для этого давайте загрузим исторические ежемесячные доходности Apple и S&P 500 (с января 2005 г. по декабрь 2014 г.). Следующий график доходности акций Apple по сравнению с доходностью S&P 500 помогает проиллюстрировать бета-версию Apple как наклон ее линии регрессии.
Вычисляя исторические данные с помощью уравнения (2), мы получаем историческую бету 1,26 ( β hist = 1,26). Предполагается, что бета-версия актива имеет свойство возврата к среднему значению, что означает, что в долгосрочной перспективе он возвращается к рыночной бета-версии 1. Таким образом, на практике историческая бета корректируется, чтобы учесть эту природу беты для расчетов ожидаемых значений. Мы корректируем историческую бета-версию Apple с помощью следующего уравнения:
где α – это скорость приближения долгосрочной бета-версии к рыночной бета, которая равна 1. Таким образом, чем выше α, тем быстрее приближается бета-версия 1. Как правило, α принимается равным 0,33. Таким образом, мы можем рассчитать скорректированную бету, скорректированную b.
βдJUсектед знак равно 0.67
Калькулятор модели оценки капитальных активов
Ожидаемая рыночная доходность (%)
Работает на
Оглавление
Калькулятор CAPM
Модель ценообразования капитальных активов (CAPM) используется в финансах для объяснения взаимосвязи между ожидаемой доходностью и риском безопасности. Этот калькулятор модели оценки капитальных активов (CAPM) можно использовать для расчета ожидаемой доходности ценной бумаги. Он использует бета акции, рыночную доходность и безрисковую ставку.
Модель ценообразования капитальных активов (CAPM)
Модель ценообразования капитальных активов (CAPM) описывает взаимосвязь между систематическими рисками и ожидаемой доходностью активов, особенно акций.1 CAPM используется в финансах для оценки рисковых ценных бумаг и получения ожидаемой доходности активов с учетом их капитальной стоимости и риска.
Инвесторы рассчитывают получить компенсацию за риск и денежную стоимость. Безрисковая ставка является частью формулы CAPM. Он учитывает временную стоимость. Инвестор берет на себя дополнительный риск, используя другие компоненты формулы CAPM.
[бета] (https://www.investopedia.com/terms/b/beta.asp) стоимость потенциальных инвестиций является мерой того, насколько рискованными будут инвестиции в портфель, аналогичный рынку. Бета больше единицы указывает на то, что акции более рискованны, чем рынок. Предполагается, что акции с коэффициентом бета ниже единицы снижают риск портфеля.
Рыночная премия – это ожидаемая доходность рынка, превышающая безрисковую ставку. Это умножается на коэффициент бета акции. Затем добавляются премия за рыночный риск и бета акции. Это должно дать инвесторам требуемую доходность и ставки дисконтирования, которые они могут использовать для определения стоимости актива.
Формула CAPM оценивает, сопоставимы ли риск и временная стоимость акции с ее ожидаемой доходностью.
Проблемы с САРМ
Формула CAPM основана на нескольких допущениях, которые оказались ложными. В основе современной финансовой теории лежат два допущения: во-первых, рынки ценных бумаг отличаются высокой конкуренцией и эффективностью (то есть информация о компаниях быстро и повсеместно доступна и усваивается), а во-вторых, на этих рынках доминируют рациональные, не склонные к риску инвесторы, которые стремятся к максимальной выгоде. удовлетворение от своих вложений.
Несмотря на эти проблемы, формула CAPM продолжает широко использоваться. Это просто и позволяет легко сравнивать варианты инвестиций.
Бета включена в формулу, поскольку предполагает, что волатильность цен на акции может использоваться для измерения риска. Движения цены в любом направлении не одинаково опасны. Поскольку доходность акций (и связанный с ней риск) обычно не распределяется, период ретроспективного анализа, используемый для определения волатильности акций, не является стандартным.
CAPM предполагает, что безрисковая процентная ставка не изменится в течение периода дисконтирования. В предыдущем примере процентная ставка по казначейским облигациям США выросла до 5% или 6 в течение 10-летнего периода. Повышение безрисковой ставки также может увеличить стоимость капитала и сделать акции более дорогими.
Рыночный портфель, используемый для расчета премии за рыночный риск, является только теоретической величиной и не может быть куплен или инвестирован в качестве опциона на акции. Инвесторы в большинстве случаев будут заменять рынок, используя основные фондовые индексы, такие как S&P 500. Это несовершенное сравнение.
Предположение САРМ о том, что будущие денежные потоки можно легко предсказать с помощью дисконтирования, является его самым серьезным недостатком. CAPM не понадобился бы, если бы инвестор мог точно предсказать будущую доходность акций.
CAPM и граница эффективности
Предполагается, что способность инвестора управлять своим риском с помощью CAPM при создании портфеля должна помочь. На следующем графике показано, как инвестор может использовать CAPM для оптимизации относительного риска доходности своего портфеля.
Этот график показывает, как более высокая ожидаемая доходность (ось Y) требует большего риска (ось X). Современная портфельная теория утверждает, что портфели с безрисковой ставкой будут иметь более высокую ожидаемую доходность. Портфель, совместимый с линией рынка капитала, превосходит любой другой портфель. Однако в какой-то момент можно построить теоретический портфель, используя CML, который дает наибольшую отдачу от принятого риска.
Хотя CML и граница эффективности представляют собой трудные для понимания концепции, они иллюстрируют важную концепцию для инвесторов: инвесторы должны делать выбор между более высокой доходностью и более высоким риском. Трудно создать портфолио, соответствующее CML. Инвесторы с большей вероятностью берут на себя слишком много рисков, чтобы получить дополнительную прибыль.
На следующей диаграмме показаны два портфеля, разработанные с учетом границы эффективности. Ожидается, что портфель А принесет 8% годовых и имеет уровень риска 10% или стандартное отклонение. Портфель B будет приносить 10% годовых, но его стандартное отклонение составляет 16%. Риск портфеля B рос быстрее, чем его ожидаемая доходность.
Эффективная граница предполагает те же предположения, что и CAPM, и может быть рассчитана только теоретически. Портфель, который существует на границе эффективности, обеспечит наибольшую доходность за принятый на себя риск. Невозможно предсказать будущие доходы, поэтому невозможно, чтобы портфель находился на границе эффективности.
CAPM — это компромисс между доходностью и риском. Однако график эффективной границы можно изменить, чтобы показать компромисс для отдельных активов. На следующей диаграмме показано, что CML был переименован в Линию рынка ценных бумаг. Вместо ожидаемого риска, показанного на оси x, используется бета акции. На рисунке видно, что бета увеличивается с единицы до двух, а также увеличивается ожидаемая доходность.
CAPM, SML и SML устанавливают связь между бета-уровнем акции и ожидаемым риском. Более высокие бета означают больший риск, но портфели акций с высоким бета могут существовать на CML, где этот компромисс приемлем.
Эти предположения о бета-версии и участниках рынка снижают ценность этих моделей. Бета не принимает во внимание относительный риск акций, которые более волатильны, чем рынок, и имеют более высокую частоту понижательных шоков по сравнению с другими акциями с аналогичным бета, но с меньшим движением цены в сторону понижения.
Практическая ценность CAPM
Может показаться трудным понять, как CAPM может быть полезен, учитывая критику и предположения, на которых он основан при построении портфеля. CAPM по-прежнему может быть полезен для оценки будущих ожиданий и их сравнения.
Представьте себе советника, предлагающего добавить акцию в портфель по цене 100 долларов за акцию. Для обоснования цены советник использует CAPM со ставкой дисконтирования 13%. Инвестиционный менеджер консультанта может сравнить эту информацию с прошлыми показателями компании и других компаний-аналогов, чтобы определить, является ли 13% разумным.
Подумайте об этом: доходность группы аналогов за последние несколько лет была чуть выше 10%, в то время как акции постоянно отставали с доходностью всего 9%. Инвестиционный менеджер не должен принимать рекомендацию консультанта без обоснования более высокой ожидаемой доходности.
Инвесторы также могут использовать такие концепции, как граница эффективности и CAPM, для оценки эффективности своего портфеля или отдельных акций по сравнению с остальными. В качестве примера предположим, что портфель инвестора за последние три года приносил 10% в год. Однако это предполагает, что стандартное отклонение (риск) составляет 10%. Среднерыночная доходность за последние три года составила 10% при уровне риска 8%.
Это наблюдение может быть использовано инвестором для проверки своего портфеля и определения того, какие активы не включены в SML. Это может помочь объяснить, почему портфель инвестора не соответствует CML. Инвесторы могут определить активы, которые непропорционально влияют на доходность или увеличивают риск в портфеле, и внести коррективы для увеличения доходности.
Для определения справедливой стоимости ценной бумаги CAPM применяет принципы современной теории портфеля. Он основан на предположениях о поведении инвесторов, распределении риска и доходности, а также основных принципах рынка. Эти предположения не соответствуют действительности. Основные концепции CAPM и границы эффективности, которые она создает, могут помочь инвесторам лучше понять взаимосвязь между ожидаемым доходом и риском, чтобы они могли принимать более обоснованные решения при добавлении ценных бумаг в свой портфель.
Автор статьи
Parmis Kazemi
Пармис — создатель контента, который любит писать и создавать новые вещи. Она также очень интересуется технологиями и любит узнавать что-то новое.
Калькулятор CAPM русский
Опубликовано: Tue May 03 2022
В категории Финансовые калькуляторы
Добавьте Калькулятор CAPM на свой сайт
Калькулятор CAPM на других языках
Другие финансовые калькуляторы
Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+
АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 г. (без ограничения срока действия).
ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.
Наверняка читателям моего T-канала и smart-lab.ru на глаза не раз попадалась аббревиатура CAPM. Если перейти на сайт с разъяснениями CAPM, то, как правило, после пяти минут чтения рука просит закрыть страницу, или просто добавить ее в закладки и благополучно забыть про нее. Это из-за того, что тема обширная, а быстрые и конкретные рецепты по применению CAPM в инвестировании «глубоко зарыты».
Для тех, кто хочет понять, как определить Ожидаемый доход акций с помощью CAPM, давайте попробуем разобраться. Те, кто уже знаком с CAPM – «Все новое — хорошо забытое старое»!
Итак, модель CAPM(от англ. ‘capitalassetpricingmodel), русская аббревиатура МОДА(Модель оценки долгосрочных активов). Её автор — экономист Гарри Марковиц. Но взаимосвязь между уровнем риска и доходностью доработали У.Шарп, Я. Мойссин и Дж. Линтером (1964-1965).
В первую очередь модель CAPM (МОДА) использовалась финансовыми менеджерами для оценки стоимости собственного капитала компании.
В свою очередь требуемая ставка доходности обычными акционерами равна стоимости собственного капитала. И когда финансовые менеджеры к-н компании решают вопрос о расширении бизнеса путем реинвестирования прибыли (то есть целесообразность реинвестирования нераспределенной прибыли обратно в бизнес), выпуска новых обыкновенных акций или долговое финансирование, то для такой оценки обычно используют следующие подходы:
- модель CAPM (Модель оценки капитальных активов),
- модель дисконтирования дивидендов и
- метод доходности облигаций с учетом премии за риск.
В рамках данного поста ограничимся моделью CAPM, тем более, что для инвестора она может послужить отличным дополнением к аналитическому арсеналу. Как бы ее не критиковали (из-за линейной взаимосвязи), именно данная модель позволяет получить ответ на то, как финансовые рынки измеряют риск и конвертируют его в ожидаемый доход.
Инвестор, который купил акции, считает доходность так:
Доходность, % = (Сумма дивидендов + Доход от изм. цены акции) / Цена покупки акций*100
Доходность, при инвестировании в акции, может как приятно удивлять инвесторов, так и разочаровывать, поскольку колебания цен на акции приводят к колебаниям их прибыли (вплоть до отрицательной), а значит, чем больше колебания цен акций, тем выше риск.
Соответственно, инвестор выбирает либо доходность депозита, где риск отсутствует, либо рынок акций, где доходность больше, но нет предсказуемости прибыли из-за колебания цен акций.
Колебания цен акций, в стандартной модели CAPM, измеряется коэффициентом Бета (β).
Бета (β) измеряет чувствительность акций по отношению к колебаниям всего рынка и вычисляется на основе статистических данных. Как правило, коэффициент Бета (β) поставляется во всех бесплатных скринерах.
Акции с β = 1 — значит акция растет или падает на ту же величину, что и индекс;
Акции с β = 1,5 — при росте/падении индекса на 1%, акция растет или падает на 1,5%
Акции с β = 0,5 — при росте/падении индекса на 1%, акция растет или падает на 0,5%Итоговая формула: Rs= Rf + βs(Rm-Rf), где:
Rs = ожидаемая доходность акций (и стоимость собственного капитала компании).
Rf = безрисковая ставка.
βs = бета-коэффициент акций.
Rm = ожидаемая доходность на фондовом рынке в целом (Индекс акций).
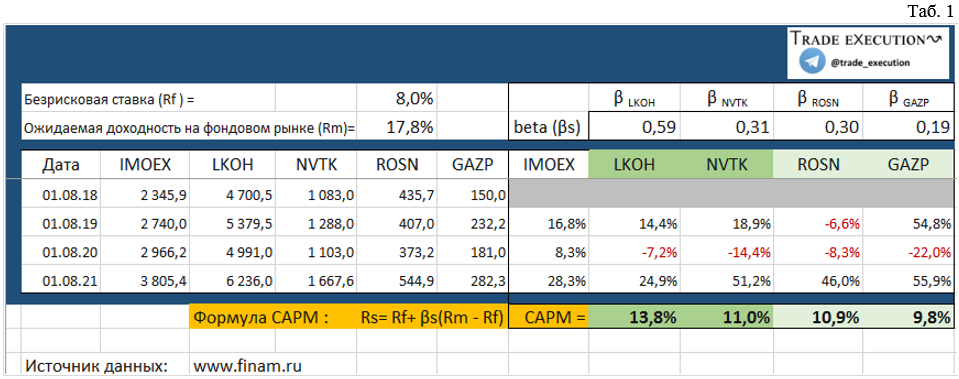
Теперь предлагаю посмотреть все расчеты на реальных цифрах. Для примера возьмем наиболее интересные акции из нефтегазовой отрасли российского рынка в сравнении с Индексом МосБиржи (IMOEX) на основе 3-х летней давности.
Итак, на реальных цифрах Дано:
Определить по стандартной модели CAPM ожидаемый доход акций на следующий год: LKOH, GAZP, NVTK, ROSN на основе 3-х летней давности при условии, что безрисковая ставка (Rf ) на следующий год останется в пределах 6,5%-9,5%.
Вычислить ожидаемую доходность на фондовом рынке (Rm) ?
Вычислить бета-коэффициент (βs) ?
Определить ожидаемый доход акций на следующий год ?
Решение:
В качестве безрисковой ставки берем будущее среднее значение (6,5%+9,5%)/2=8%
Ожидаемую доходность на фондовом рынке (Rm) = среднегодовая доходность индекса за три года
βs рассчитываем по готовой формуле1 в excel =НАКЛОН (Диапазон доходности Индекса МосБиржи по годам; Диапазон доходности Акции по годам)
1При помощи функции НАКЛОН (в англоязычной версии – SLOPE) определяем коэффициент наклона между массивами данных. Итоговое значение и является бета коэффициентом.
Ожидаемый доход каждой акции рассчитываем по формуле CAPM (Rs= Rf+ βs(Rm-Rf))
Вывод: Исходя из расчетов (Таб. 1) хорошо прослеживается связь ожидаемого дохода и коэффициент — бета (βs). Чем коэффициент выше, тем больше ожидаемый доход и наоборот. Акции LKOH, из представленной выборки с ожидаемым доходом на следующие год 13,8%, принято считать наиболее рискованными, поскольку бета выше. Соответственно более стабильной в нашем случае принято считать акции GAZP с ожидаемым доходом 9,8% и более низкой бетой.
Тема для спора: Проблема данного подхода в том, что бета-коэффициенты нестабильны с течением времени. Это создает трудности, когда бета-коэффициенты, полученные по историческим данным, используются для расчетов ожидаемого дохода акций. Также Оценка будущей безрисковой ставки тоже подвержена ошибкам. Однако, несмотря на все недостатки, измерения ожидаемого дохода по модели CAPM выглядят не хуже, чем другие существующие подходы Оценок акций.
Ее ключевым преимуществом является то, что она количественно оценивает риск и обеспечивает объективный подход для перевода показателей риска в оценку ожидаемой прибыли.
Если понравился пост, поставьте ♥ лайк!
p.s. В Telegram-канале в комментариях к посту можно скачать файл excel со всеми расчетами. Также не забудьте подписаться на мой Telegram-канал: @trade_execution
Стоимость обыкновенного акционерного капитала.
Стоимость обычного акционерного капитала, (( r_e )), обычно называемая просто как стоимость собственного капитала или затраты на капитал, является ставкой доходности, требуемой обычными акционерами компании.
Компания может увеличить обычный капитал посредством реинвестирования прибыли (то есть нераспределенной прибыли) или путем выпуска новых обыкновенных акций.
Как мы обсуждали ранее, оценка стоимости собственного капитала сложна из-за неопределенного характера будущих денежных потоков с точки зрения сумм и сроков.
Для такой оценки обычно используют следующие подходы:
- модель CAPM (Модель оценки капитальных активов),
- модель дисконтирования дивидендов и
- метод доходности облигаций с учетом премии за риск.
Модель оценки капитальных активов (CAPM).
Модель оценки капитальных активов (CAPM, capital asset pricing model), упоминаемая также как модель оценки долгосрочных активов (МОДА) или модель ценообразования по капитальным активам, основана на том, что ожидаемая доходность акций ( E(R_i) ), является суммой безрисковой процентной ставки ( R_F ) и премии за рыночный риск акций ( beta_i (R_M — R_F ) ):
( dstl E(R_i) = R_F + beta_i left[ E(R_M) — R_F right] ) (Формула 4)
где
- ( beta_i ) = чувствительность доходности акций (i) к изменениям рыночной доходности,
- ( E(R_M) ) = ожидаемая на рынке доходность,
- ( E(R_M) — R_F ) = ожидаемая рыночная премия за риск (рисковая надбавка).
Безрисковый актив определяется здесь как актив, не имеющий риска дефолта. Как правило, в качестве безрисковой ставки признается доходность государственных долговых инструментов.
В целом, при выборе соответствующей безрисковой ставки необходимо руководствоваться длительностью прогнозирования денежных потоков. Если мы оцениваем проект длительностью 10 лет, то мы вероятно используем ставку 10-летних государственных казначейских облигаций.
Пример 7. Использование CAPM для оценки стоимости собственного капитала.
Компания Valence Industries хочет выяснить затраты на свой собственный капитал. Финансовый директор считает, что безрисковая ставка составляет 5%, премия за риск составляет 7%, а бета-коэффициент составляет 1.5.
Какой будет стоимость капитала (затраты на собственный капитал) Valence Industries при использовании метода CAPM?
Решение:
Стоимость капитала = 5% + 1.5 (7%) = 15.5%.
Ожидаемый рыночная премия за риск или ( E(R_M) — R_F ), является премией, которую инвесторы требуют за инвестирование в рыночный портфель относительно безрисковой ставки.
На практике, при использовании CAPM для оценки стоимости собственного капитала, мы обычно оцениваем бета-коэффициент относительно рыночного индекса акций. В этом случае оценка рыночной премии, которую мы используем, на самом деле является оценкой премии за риск приобретения акций или премией за акции (ERP, англ. ‘equity risk premium’).
Альтернативным способом учесть в CAPM риски, которые могут выходить за рамки исключительно рыночного портфеля, является многофакторная модель, которая включает в себя факторы других источников риска (т.е. риска, за который инвесторы требуют компенсацию), включая макроэкономические факторы и специфические для компании факторы.
В целом:
(
deffact{{normalsize text{Фактор премии за риск}}}
dstl begin{aligned}
E(R_i) = R_F &+ beta_{i1} (fact)_1 \ &+ beta_{i2} (fact)_2 + ldots \ &+ beta_{ij} (fact)_j
end{aligned} ) (Формула 5)
где
- ( beta_{ij} ) = чувствительность акций (i) к изменениям в (j)-м факторе,
- ( (fact)_j )= Ожидаемая премия за риск для фактора (j).
Основная идея таких многофакторных моделей заключается в том, что бета-коэффициент CAPM может не охватывать все риски, особенно в глобальном контексте, которые включают риски инфляции, бизнес-цикла, процентной ставки, обменного курса и риски дефолта.
Пример мультифакторной модели — трехфакторная модель Фама и Френча [Eugene Fama и Kenneth French, “The Cross-Section of Expected Stock Returns,” Journal of Finance, Vol. 47, No. 2 (1992), стр. 427-465], которая включает факторы рынка, капитализацию и соотношение балансовой и рыночной стоимости собственного капитала.
Существует несколько способов оценить премию за риск акций, хотя нет общепринятого мнения о наилучшем подходе. Далее мы рассмотрим три таких способа: подход исторической премии за риск, подход на основе модели дисконтирования дивидендов и метод опроса.
Исторический подход к оценке премии за риск акций (англ. ‘historical equity risk premium approach’) — это хорошо отработанный подход, основанный на предположении, что реализованная премия за риск акций, наблюдаемая в течение длительного периода времени, является хорошим индикатором ожидаемой премии за риск акций.
Этот подход требует сопоставления исторических данных, чтобы найти среднюю ставку доходности рыночного портфеля для определенной страны и среднюю ставку доходности для безрисковой ставки в этой стране. Например, аналитик может использовать историческую доходность индекса Topix для оценки премии за риск для японских акций.
Исключительный бычий рынок, наблюдаемый во второй половине 1990-х годов, а также крах технологического пузыря (известный также как пузырь доткомов), который последовал затем в течение 2000-2002 годов, напоминает нам, что период для таких оценок должен охватывать полные рыночные циклы.
Элрой Димсон, Пол Марш и Майк Стантон (Elroy Dimson, Paul Marsh и Mike Staunton) провели анализ премий за риск акций, наблюдаемых на рынках в 21 странах, включая США, в течение 1900-2017 годов.
Эти исследователи обнаружили, что годовая премия за риск акций США, относительно казначейских векселей США составила 5.6% (среднее геометрическое) и 7.5% (среднее арифметическое).
Они также обнаружили, что годовая премия за риск акций США относительно гособлигаций составила 4.4% (среднее геометрическое) и 6.5% (среднее арифметическое).
Джереми Сигел изучил более длительные временные ряды рыночной доходности, охватывающих период с 1802 по 2004 год и показывающие доходность акций 6.82% и премию за риск акций в диапазоне от 3.31% до 5.36%.
См. Jeremy J. Siegel, “Perspectives on the Equity Risk Premium,” Financial Analysts Journal, Vol. 61, No. 6 (Ноябрь / Декабрь 2005), стр. 61-73.
Обратите внимание, что среднее арифметическое больше чем среднее геометрическое в результате значительной волатильности наблюдаемой рыночной ставки доходности и безрисковой ставки.
При допущении о неизменном распределении доходности на протяжении всего времени, арифметическое среднее представляет собой несмещенную оценку ожидаемой премии за риск для одного периода, но геометрическое среднее лучше отражает темпы роста в течение нескольких периодов.
Помимо метода усреднения (геометрического или арифметического), оценки исторической премии за риск акций различаются в зависимости от:
- предполагаемого инвестиционного горизонта (короткие, промежуточные и длительные), того, зависят ли от влияния некоторой переменной или не зависят,
- того, наблюдаются на рынке США или других глобальных рынках,
- источника данных,
- наблюдаемого периода, и
- того, оценивается ли номинальная или реальная доходность.
В Иллюстрации 2 показаны исторические оценки премии риска акций на 20 развитых рынках из исследования Димсона, Марша и Стантона.
Иллюстрация 2. Премии за риск акций относительно гособлигаций (c 1900 по 2017 года).
|
Среднее |
Среднее |
|
|
Австралия |
5.0% |
6.6% |
|
Бельгия |
2.2 |
4.3 |
|
Канада |
3.5 |
5.1 |
|
Дания |
2.2 |
3.8 |
|
Финляндия |
5.2 |
8.7 |
|
Франция |
3.1 |
5.4 |
|
Германия |
5.1 |
8.4 |
|
Ирландия |
2.7 |
4.7 |
|
Италия |
3.2 |
6.5 |
|
Япония |
5.1 |
9.1 |
|
Нидерланды |
3.3 |
5.6 |
|
Новая Зеландия |
4.0 |
5.6 |
|
Норвегия |
2.5 |
5.4 |
|
Португалия |
5.3 |
9.4 |
|
Южная Африка |
5.3 |
7.1 |
|
Испания |
1.8 |
3.8 |
|
Швеция |
3.1 |
5.3 |
|
Швейцария |
2.2 |
3.7 |
|
Соединенное Королевство |
3.7 |
5.0 |
|
США |
4.4 |
6.5 |
|
Мир |
3.2 |
4.4 |
Примечание: Германия исключает 1922-23 годы.
Источник: Dimson, Marsh, and Staunton (2018).
Чтобы проиллюстрировать применение исторического метода в CAPM, предположим, что мы используем историческое среднее геометрическое для акций США в 4.4%, чтобы оценить Apple Computer по состоянию на начало августа 2018 года.
Согласно Yahoo Finance, Apple имела бета-коэффициент 1.14 в то время.
Используя 10-летнюю доходность казначейских векселей США в 3.0% в качестве безрисковой ставки, мы оцениваем, что стоимость собственного капитала Apple Computer составляет:
3.0% + 1.14 (4.4%) = 8.016%.
Исторический подход имеет несколько ограничений.
Одно из ограничений состоит в том, что уровень риска индекса акций может меняться со временем. Другое состоит в том, что подверженность инвесторов риску также может измениться со временем.
И еще одно ограничение состоит в том, что оценки чувствительны к методу оценки и охватываемому историческому периоду.
Пример 8. Оценка премии за риск акций при использовании исторических ставок доходности.
Предположим, что среднее арифметическое казначейских облигаций США, наблюдаемое за последние 90 лет, является несмещенной оценкой для безрисковой ставки и составляет 4.88%.
Аналогичным образом, предположим, что средняя арифметическая доходность на рынке, наблюдаемая за последние 90 лет, является несмещенной оценкой для ожидаемой доходности рынка.
Средняя ставка доходности рынка составила 9.65%. Рассчитайте премию за риск акций.
Решение:
( {rm ERP} = overline R_M — overline R_F ) = 9.65% — 4.88% = 4.77%
Вторым подходом для оценки премии за риск акций является подход на основе модели дисконтирования дивидендов (англ. ‘dividend discount model based approach’), называемый также подходом подразумеваемого риска, который реализуется с использованием модели роста Гордона (также известной как модель дисконтирования дивидендов с постоянным ростом).
На развитых рынках корпоративная доходность часто соответствует, по крайней мере, приблизительно, допущению этой модели о тенденции долгосрочного роста.
Мы получаем премию за риск, анализируя, как рынок оценивает индекс акций. То есть, мы используем связь между стоимостью индекса и ожидаемыми дивидендами, при условии постоянного роста дивидендов:
( dstl P_0 = { D_1 over r_e — g } )
где:
- ( P_0 ) является текущей рыночной стоимостью индекса акций,
- ( D_1 ) — это дивиденды, ожидаемые в следующий период в индексе,
- ( r_e ) — это требуемая ставка доходности на рынке, а
- ( g ) — ожидаемый темп роста дивидендов.
Мы находим требуемую ставку доходности на рынке следующим образом:
( dstl r_e = { D_1 over P_0 } + g ) (Формула 6)
Следовательно, ожидаемая доходность на рынке является суммой доходности дивидендов и темпов роста дивидендов. Таким образом, премия за риск акций является разницей между ожидаемой доходностью на рынке и безрисковой ставки.
Предположим, что ожидаемая доходность дивидендов в индексе акций составляет 5%, а ожидаемый темп роста дивидендов в индексе составляет 2%. Ожидаемая доходность на рынке согласно модели роста Гордона составит:
( E(R_m) ) = 5% + 2% = 7%
Безрисковая ставка в 3.8% подразумевает премию за риска акций:
7% — 3.8% = 3.2%.
Другой подход к оценке премии за риск акций является довольно прямым: запросите у группы финансовых экспертов их оценки и выведите из них средний ответ. Этот подход называется методом опроса или исследования (англ. ‘survey approach’).
Например, опрос финансовых директоров США в декабре 2017 года обнаружил, что средняя ожидаемая премия за риск в США в течение следующих 10 лет составляла 4.42%, а медиана составлял 3.63%.
См. исследование: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3151162
Получив оценку премии за риск, мы можем уточнить эту оценку для конкретной компании или проекта, скорректировав ее с учетом конкретного систематического риска проекта.
Мы делаем корректировку для конкретного систематического риска, умножая рыночную премию за риск на бета-коэффициент. Полученную таким образом премию за риск компании или проекта, мы тогда прибавляем к безрисковой ставке, чтобы определить затраты на капитала в рамках модели CAPM.
Некоторые исследователи утверждают, что премия за риск акций должна отражать премию за риск конкретной страны.
Например, транснациональная компания или проект могут иметь более высокую стоимость капитала, чем сопоставимая отечественная компания из-за политического риска, валютного риска или более высоких агентских расходов. В большинстве случаев этот риск несистематичен и, следовательно, не влияет на оценку стоимости капитала.