Mathematical modeling is now the basis of managerial decision-making in modern business, this article on the example of LLC «Zheldorservis» clearly presents theoretical as well as empirical evidence that mathematical modeling helps to solve and answer the above questions.
Keywords: method, economic model, Economics, economic processes.
В настоящее время предпринимательство в России активно развивается. И в условиях такой тенденции у предпринимателей часто возникают вопросы: «Как увеличить прибыль?», «Какие инструменты использовать?» «Как заполучить выигрышную позицию в сравнении с конкурентами?». В последнее время всё чаще для решения этих проблем используются математические модели. И появляются уже другие вопросы: «Как правильно строить математические модели», «Как их использовать?», «Как с их помощью можно получить конкурентное преимущество?». Математическое моделирование в настоящее время является основой принятия управленческих решений в современном бизнесе, в данной статье на примере компании ООО «Желдорсервис» наглядно представлено теоретическое, а также практическое доказательство того, что математическое моделирование помогает успешно решить и ответить на вышеупомянутые вопросы.
При помощи математического моделирования строятся различные модели, описывающие различные ситуации, включающие в себя данные о конкретном предприятии. Построение и использование этих моделей способствует принятию важных управленческих решений в различных сферах, в частности — в бизнесе. Все задачи имеют многовариантные решения, которые могут быть найдены с помощью составления и построения математических моделей.
1.Математический инструментарий принятия решений компании ООО «Желдорсервис»
Данный инструментарий (экономико-математические модели и методы — ЭМММ) представляет собой логический системный подход к решению проблемы управления (рис. 1).
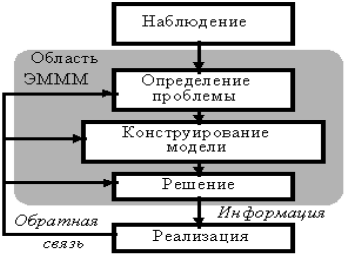
Рис. 1 Использование ЭМММ при принятии решения
Менеджер не прямо применяет полученный результат как решение, а сравнивает его со своими оценками и прогнозами. Если менеджер не использует результаты ЭМММ, то это означает, что они не могут быть реализованы. Если это так, то необходимо ввести дополнительные ресурсы или усилия при решении проблемы, конструировании модели и ее решении. Результаты моделирования и решения основываются на оригинальной модели, которая в процессе испытания в различных условиях, а также будущих решений менеджера, может быть изменена.
На практике в менеджменте наибольшее значение придается следующим моделям:
сетевым;
имитационным;
теории очередей (задачам массового обслуживания);
линейному программированию;
графам (деревьям) решений;
анализу замещения;
интегральному программированию.
Математические модели используются при решении разного типа задач. Рассмотрим несколько примеров их использования в реальной деятельности компании ООО «Желдорсервис». Первое, что стоит отметить, изучают издержки фирмы на простейших математических моделях, которые строятся на линейной зависимости всех издержек от постоянных и переменных. В данном случае рассматривается таблица, которую предлагается заполнить, используя простые формулы.
Таблица 1
Исходные данные
|
Q |
AFC |
AVC |
VC |
AC |
MC |
TC |
|
1 |
20 |
|||||
|
2 |
79 |
|||||
|
3 |
54 |
|||||
|
4 |
17 |
|||||
|
5 |
24 |
200 |
TC=VC+FC, AFC=FC/Q, AVC=VC/Q, AC=TC/Q, MC=(TC)’
Таблица 2
Решение задачи
|
Q |
AFC |
AVC |
VC |
AC |
MC |
TC |
|
1 |
120 |
18 |
18 |
138 |
20 |
138 |
|
2 |
60 |
19 |
38 |
79 |
16 |
158 |
|
3 |
40 |
18 |
54 |
58 |
14 |
174 |
|
4 |
30 |
17 |
68 |
47 |
12 |
188 |
|
5 |
24 |
16 |
80 |
40 |
— |
200 |
В результате человек, решающий данную задачу получает показатели, которые может иметь фирма, и в дальнейшем использовать их для определения оптимального выпуска и цены в различных рыночных условиях.
После того, как изучается взаимосвязь издержек, решается задача на определение оптимума фирмы. В бизнесе более вероятны ситуации, когда математическая модель может стать ключом к решению поставленной задачи, в частности, при определении антикризисной стратегии или способе осуществления конкурентной борьбы. Например, когда происходит «ценовая война». Фирмы или группа фирм устанавливают заниженные цены и работают в убыток для того, чтобы освободить пространство на рынке. Здесь модель чётко покажет, сколько может работать фирма в условиях такой борьбы, и даст прогноз, сколько смогут продержаться конкуренты.
2. Использование математического инструментария в финансовой сфере компании ООО «Желдорсервис»
Математический инструментарий активно используется в финансовой сфере компании ООО «Желдорсервис». Для определения доходности компаний и инвестиционных портфелей в зависимости от различных факторов используются такие коэффициенты, как Альфа, Бета, Шарпа, Сортино и Треёнора. ООО «Желдорсервис» необходимо знать, насколько доходным будет тот или иной портфель. Кратко остановимся на этих ключевых показателях, используемых в работе компании.
Коэффициент альфа — параметр, с помощью которого можно точно оценить эффективность управления капиталом при учете рисковой составляющей. Коэффициент альфа отображает, насколько результаты работы на рынке зависят от качества торговой системы, а не от рыночных колебаний. Бета-коэффициент — показатель, рассчитываемый для портфеля ценных бумаг. Является мерой рыночного риска, отражая изменчивость доходности портфеля по отношению к доходности другого портфеля, в роли которого часто выступает среднерыночный портфель. Коэффициент Шарпа — показатель эффективности инвестиционного портфеля (актива), который вычисляется как отношение средней премии за риск к среднему отклонению портфеля. Другими словами, этот коэффициент показывает связь доходности портфеля и его волатильности. Коэффициент Сортино — представляет собой показатель, обуславливающий связь между изменчивостью портфеля и доходностью. Отличается он от коэффициента Шарпа тем, что при его расчёте используется так называемая «волатильность вниз». В этом случае волатильность рассчитывается по доходностям ниже минимального допустимого уровня доходности портфеля (MAR). Коэффициент Трейнора —отношение средней доходности, превышающей без рисковую процентную ставку, к систематическому риску β.
Данные показатели являются базовым инструментарием при определении доходности портфеля компании ООО «Желдорсервис». Само собой, каждый из них представляет собой математическую формулу с чётко определёнными переменными. С другой стороны, практически каждый из них имеет определённые ограничения, которые объясняют неточности всей модели в целом. Построение моделей помогает решить многие проблемы в бизнесе, если их рационально использовать в сочетании с другими математическими методами. Тем не менее, нужно всегда учитывать экономическую составляющую и понимать сущность экономических процессов. Из вышесказанного следует, что работать модели могут как в определённом конкретном случае, так и при решении общих задач, стоящих перед компанией.
3. Этапы экономико-математического моделирования в компании ООО «Желдорсервис»
Под применением экономико-математических моделей подразумевается не просто выполнение разнообразных экономических расчетов, а использование математики в целях нахождения наиболее выгодных и удачных экономических решений, а также изучения экономических зависимостей и закономерностей, получения новых теоретических выводов.
Синтез инновационных экономических и математических знаний даёт новые возможности в сфере экономического анализа.
Рассмотрим содержание процесса экономико-математического моделирования поэтапно. Обычно выделяют шесть основных этапов:
- Определение и постановка экономической проблемы, ее рассмотрение и тщательный анализ
- Построение математической модели;
- Математический анализ построенной модели;
- Подготовка исходной информационной базы;
- Решение поставленной задачи в числах;
- Анализ, обработка и рассмотрение возможных вариантов применения полученных числовых результатов,
Рассмотрим этапы процесса экономико-математического моделирования более развернуто и в примерах.
- На этом этапе происходит четкое формулирование сути проблемы, принимаемые допущения, а также происходит четкая постановка вопросов, на которые необходимо будет найти ответы. Этот этап подразумевает выделение важнейших черт и свойств объекта моделирования, второстепенные черты уходят на второй план. Тщательно изучается структура объекта, взаимосвязь составляющих его элементов, также обычно формулируется предварительная гипотеза, разъясняющая характер поведения и развития объекта.
- Построение математической модели означает представление нашей поставленной экономической проблемы в виде определенных математических зависимостей и отношений: уравнений, неравенств, функций. Как в любой модели, сначала строится каркас- основная типовая конструкция, затем каркас совершенствуется при помощи добавления деталей и параметров. Неправильно полагать, что чем больше фактов учитывает модель, тем она лучше «работает» и дает лучшие результаты. То же можно сказать о таких характеристиках сложности модели, как используемые формы математических зависимостей (линейные и нелинейные), учет факторов случайности т неопределенности и т. д. Положение о том, что, чем сложнее модель, тем она лучше, является ошибочным. Громоздкость и ёмкость модели затрудняют процесс исследования.
Если планируется усложнить модель, с целью сделать ее более точной и подробной, нужно помнить и справедливо оценивать, будут ли соответствовать затраченные силы на вычисления точности прогнозируемых результатов. И обратно, если принято решение исключить какой-либо элемент из модели, чтобы упростить модель, необходимо оценить вероятные потери в ее достоверности.
- На этом этапе в основном применяются математические приемы исследования.
Одна из наиболее важных задач на этапе — доказательство возможности существования решений в сформулированной модели. Если доказано, что поставленная математическая задача не имеет решения, то автоматически исчезает смысл дальнейшей работы по первоначальному варианту модели, а значит, следует скорректировать либо саму постановку экономической задачи, либо способы ее точного математического представления — формализации. Аналитической исследование модели имеет одно преимущество по отношению к численному (эмпирическому): выводы, которые мы получаем сохраняют своё значение при подстановке различных конкретных значений внешних и внутренних параметров модели, то есть мы имеем своеобразный шаблон.
- Моделирование ставит жесткие требования к систематизированию исходной информации. В то же время реальные возможности получения информации ограничивают выбор моделей, предназначаемых для практического использования. В случае, если нам недостаточно одной лишь подготовки определенной информации, а необходимы дополнительные затраты на подготовку иных информационных массивов, нужно помнить, что такие затраты не должны превышать получаемый эффект от использования дополнительной информации. В процессе подготовки информационной базы часто и широко используются методы теории вероятностей, а также теоретической и математической статистики. При системном экономико-математическом моделировании информационные потоки взаимосвязаны друг с другом: выходные результаты функционирования одних моделей являются исходной информацией, используемой в других моделях.
- Непосредственный этап численного решения задачи. Разработка алгоритмов, составление программ на ЭВМ и само проведение расчетов. Сложности на этом этапе могут возникать ввиду большого объема решаемых экономических задач и информационных массивов для обработки. Непосредственное исследование в числах может значительно дополнить результаты аналитического исследования, а для многих моделей оно даже является единственно осуществимым. Количество задач, которые доступны к решению численными методами, значительно больше, чем количество задач, которые могут быть подвержены аналитическому исследованию.
- На этом заключительном этапе цикла основным и самым важным является вопрос о правильности и полноте полученных результатов моделирования, а также о возможности реального практического применения этих результатов. Неформальный, обычно человеческий анализ теоретических выводов и численных результатов, которые были получены на выходе из модели, сопоставление их с имеющимися знаниями, информационными массивами и фактами действительности также позволяют обнаруживать недостатки постановки экономической задачи, сконструированной математической модели, а также ее информационного и математического обеспечения.
4. Пример применения простейшей двухпродуктовой балансовой экономико-математической модели ООО «Желдорсервис»
Пусть производится два товара, один — в количестве x1 и другой — в количестве x2 (измеряются в одинаковых единицах). На производство первого товара тратится 0,1 общего выпуска этого же товара и 0,15 единиц второго товара. Кроме того, 3300 единиц первого товара производится на другие нужды. На производство единицы второго товара затрачивается 0,2 единицы первого товара и 0,05 единиц второго товара. Кроме того, 6600 единиц второго товара производится на другие нужды. Задача: определить требуемые объемы производства одного и второго товара (m1 и m2)
Двухпродуктовая балансовая модель выглядит следующим образом:
m1 — объем производства первого товара;
m2 — объем производства второго товара;
b11 — доля первого товара, затрачиваемая на его же производство;
b12 — доля первого товара, затрачиваемая на производство второго;
b21 — доля второго товара, затрачиваемая на производство первого;
b22 — доля второго товара, затрачиваемая на его же производство;
m1v — объем производства первого товара на другие нужды;
m2v — объем производства второго товара на другие нужды.
Приводимая простейшая балансовая модель представляет систему двух линейных уравнений относительно неизвестных m1 и m2.
Согласно условиям задачи: b11== 0,1; b12 = 0,15; b21 = 0,2; b22 = 0,05; m1v =3300; m2v = 6600.
В итоге приходим к системе уравнений баланса:
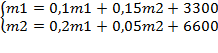
Решаем систему, находим искомые объемы производства: m1 = 5000 единиц; m2 = 8000 единиц. Исходную модель можно использовать для поиска любых элементов системы при заданных значениям других величин, включенных в систему.
4. Экономико-математическая модель на примере задачи планирования производства ООО «Желдорсервис»
Таблица 3
Данные задачи по планированию производства
|
Виды сырья |
Запасы сырья |
Количество единиц сырья, затрачиваемых на изготовление единицы продукции |
|
|
P1 |
P2 |
||
|
S1 S2 S3 |
b1 b2 b3 |
a11 a21 a31 |
a12 a22 a32 |
|
Прибыль от единицы продукции (в руб.) |
с1 |
c2 |
|
Для изготовления двух видов продуктовP1 и P2 используют три вида сырья: S1, S2 и S3. В таблице представлены запасы сырья, количество единиц сырья, затрачиваемых на изготовление единицы продукции и величина прибыли, получаемая от единицы продукции.
Задача: составить план выпуска продукции, чтобы получать максимально возможную прибыль при реализации.
Далее переходим к составлению экономико-математической модели задачи.
Пусть x1, x2 — количество единиц продукции P1 и P2 соответственно, запланированных к производству. Тогда учитывая количество единиц сырья, которые затрачиваются на изготовление единицы продукции, а также запасы сырья получают систему неравенств.
Суммарная прибыль F(x) составит c1x1 руб. от реализации продукции P1 и c2x2 руб. — от реализации продукции P2, т. е.
F(x)=c1x1+c2x2
Итого получаем экономико-математическую модель задачи: найти такой план выпуска продукции X=(x1,x2), удовлетворяющий системе неравенств и условию x1>=0; x2>=0, при котором функция F(x) будет принимать максимальное значение.
Задачу легко обобщить, если будет выпускаться n видов продукции с использованием m видов сырья.
5. Актуальность применения экономико-математического моделирования
Экономико-математическое моделирование в настоящее время является неотъемлемой частью любого исследования в области экономики. Активное развитие математического анализа, исследования и анализа операций, теории вероятностей и математической статистики повлияло на развитие формирования разнообразных моделей экономики.
В течение последних 30–40 лет методы моделирования в экономике разрабатывались особенно прогрессивно. В основном создание и развитие этих методов было предназначено для достижения теоретических целей экономического анализа и для реализации практических целей структурного планирования, прогноза и управления.
Объединяя в себе основные процессы, экономические модели по содержанию включают в себя: производство, планирование, управление, финансы и т. д. Однако в каждой из соответствующих моделей упор всегда делается на какой-нибудь один процесс, в то время как все остальные включены туда в сокращенном упрощенном виде.
Применение экономико-математических моделей в настоящее время является очень актуальнымпри решении экономических задач. Тему делает актуальным то, что применение математических методов существенно увеличивает и преумножает возможности экономического анализа, позволяет определить новые постановки экономических задач, повышает выгоду принимаемых управленческих решений.
Экономические задачи, которые решаются в процессе этапа финансового анализа, планирования, проектирования и напрямую направлены на определение искомых неизвестных величин на основе известных входных данных, не всегда удается свести лишь к расчетам, в отличие от математических задач. Решение экономических задач сопровождается поиском необходимых недостающих данных, экспертным обсуждением и оцениванием, принятием дополнительных решений.
Актуальность применения экономико-математических моделей также подтверждается тем, что они используются не только в рамках производства и с точки зрения глобальной экономики, но и всеми нами в повседневной жизни. Кроме того, каждый человек старается максимально выгодно для себя использовать имеющуюся у него «информационную базу», качественно спланировать свои действия, иначе: смоделировать своё поведение. Простой пример: модель планирования и распределения семейного бюджета.
Экономико-математические методы тесно взаимодействуют и напрямую связаны с инновационной сферой, и, разумеется, применимы не только для отдельных индивидов, но и для общества в целом.
В экономической и управленческой сфере деятельности экономико-математические методы являются одним из важнейших «помощников», позволяющих принимать верные, выгодные разумные решения.
Впрочем, далеко не во всех случаях данные, полученные на выходе из экономико-математических моделей, могут использоваться непосредственно как готовые управленческие решения. Чаще всего они лишь являются вспомогательными, консультирующими средствами, принятие же непосредственно управленческих решений остается за человеком. Экономические и социально-экономические процессы очень сложны. Экономико-математические модели являются лишь вспомогательными элементами в сложном процессе взаимодействия вычислительных машин и человека, планирования и управления.
Применение экономико-математических методов в различных областях однозначно можно считать эффективным потому, что экономические объекты, как микро-, так и макроуровней можно рассматривать с точки зрения системного подхода. Кроме того, присутствие таких характеристик поведения экономических систем, как: динамичность, противоречивость и неоднозначность поведения, тенденция к ухудшению, подверженность воздействию внешних факторов предопределяет выбор метода их исследования.
В современном бизнесе всё чаще используются математические средства для определения оптимальной стратегии поведения фирмы. Моделирование может использоваться во многих целях, например: определение антикризисной стратегии — математически определяется поведение фирмы в резко меняющихся условиях, причём не только при резком или затяжном спаде, но и на подъёме экономической конъюнктуры; конкурирование с другими фирмами — высчитывается оптимальная стратегия взаимодействия с конкурентами на рынке; расширение производства на своём рынке — этот процесс необходимо планировать и моделировать так же точно, как предыдущие, так как при принятии управленческих решений в этом случае существует риск не просто провалить поставленную задачу, но и принести огромные убытки фирме; по аналогии — сокращение производства; выход на рынки других продуктов или на международную торговлю — при принятии такого решения фирма должна быть уверена, что это не будет стоить больше, чем может принести, для чего и будет строиться множество математических моделей для прогнозирования последствий осуществления таких задач.
В настоящее время идет поиск новых математических понятий и методов, которые будут полезны для построения и исследования, как единичных моделей, так и их систем. Системы представляют собой сложные комплексы с переменной структурой, изменчивым характером, содержащие недостаточную и не полностью формализованную информацию. Все это делает математико-статистическое моделирование, машинную имитацию всё более влиятельными и используемыми разделами математики в современной экономике.
Изучение математических дисциплин и методов, которые составляют основу современного аппарата моделирования в экономике, позволит специалистам в будущем сформировать необходимые составляющие мышления — уровень, кругозор и культуру, которые понадобятся профессионала своего дела, как для успешной работы, так и для совершенствования знаний и повышения своей квалификации. Обосновано, что применение экономико-математических методов позволяет значительно повысить качество и выгоду принимаемых решений.
Литература:
- http://www.dginh.ru/content/glavnay/ucheb_deyatel/uposob/up-fgos-14–15-pmit-15.pdf
- Баканов М. И., Мельник М. В., Шеремет А. Д. Теория экономического анализа. — М.: Финансы и статистика, 2005,
- Лотов А. В. Введение в экономико-математическое моделирование. — М.:Наука, 2008.
- http://www.imf.org/external/pubs/ft/fandd/basics/models.htm
- http://bibliofond.ru/view.aspx?id=560479
- http://economic_mathematics.academic.ru/5085
- http://www.grandars.ru/student/vysshaya-matematika/ekonomiko-matematicheskaya-model.html
- http://www.math.mrsu.ru/text/courses/method/primer_linprog_zad.htm
- Годин В. В. Информационное обеспечение управленческой деятельности / В.ВГодин, И. К. Корнеев. — М.: Мастерство, Высшая школа, 2001;
- Менеджмент: учебник / Э. М. Коротков. — М.: Издательство Юрайт, 2010, — 640 с. — (Университеты России);
- Прохоров А. П. Русская модель управления. — М.: Эксмо, 2006;
- http://www.unn.ru/books/met_files/EconMatMetMod.pdf
Основные термины (генерируются автоматически): модель, решение, задача, экономико-математическое моделирование, AFC, AVC, вид сырья, математическая модель, математическое моделирование, экономический анализ.

Экономико-математические модели могут предназначаться для исследования разных сторон народного хозяйства (в частности, его производственно-технологической, социальной, территориальной структур) и его отдельных частей. При классификации моделей по исследуемым экономическим процессам и содержательной проблематике можно выделить модели народного хозяйства в целом и его подсистем – отраслей, регионов и т.д., комплексы моделей производства, потребления, формирования и распределения доходов, трудовых ресурсов, ценообразования, финансовых связей и т.п.
Остановимся более подробно на характеристике таких классов экономико-математических моделей, с которыми связаны наибольшие особенности методологии и техники моделирования.
В соответствии с общей классификацией математических моделей они подразделяются на функциональные и структурные, а также включают промежуточные формы (структурно-функциональные). В исследованиях на народнохозяйственном уровне чаще применяются структурные модели, поскольку для планирования и управления большое значение имеют взаимосвязи подсистем.
Типичными структурными моделями являются модели межотраслевых связей. Функциональные модели широко применяются в экономическом регулировании, когда на поведение объекта (“выход”) воздействуют путем изменения “входа”. Примером может служить модель поведения потребителей в условиях товарно-денежных отношений.
Один и тот же объект может описываться одновременно и структурой, и функциональной моделью. Так, например, для планирования отдельной отраслевой системы используется структурная модель, а на народнохозяйственном уровне каждая отрасль может быть представлена функциональной моделью.
Выше уже показывались различия между моделями дескриптивными и нормативными. Дескриптивные модели отвечают на вопрос: как это происходит? или как это вероятнее всего может дальше развиваться? т.е. они только объясняют наблюдаемые факты или дают вероятный прогноз. Нормативные модели отвечают на вопрос: как это должно быть? т.е. предполагают целенаправленную деятельность. Типичным примером нормативных моделей являются модели оптимального планирования, формализующие тем или иным способом цели экономического развития, возможности и средства их достижения.
Применение дескриптивного подхода в моделировании экономики объясняется необходимостью эмпирического выявления различных зависимостей в экономике, установления статистических закономерностей экономического поведения социальных групп, изучения вероятных путей развития каких-либо процессов при неизменяющихся условиях или протекающих без внешних воздействий.
Примерами дескриптивных моделей являются производственные функции и функции покупательского спроса, построенные на основе обработки статистических данных.
Является ли экономико-математическая модель дескриптивной или нормативной, зависит не только от ее математической структуры, но от характера использования этой модели. Например, модель межотраслевого баланса дескриптивна, если она используется для анализа пропорций прошлого периода. Но эта же математическая модель становится нормативной, когда она применяется для расчетов сбалансированных вариантов развития народного хозяйства, удовлетворяющих конечные потребности общества при плановых нормативах производственных затрат.
Многие экономико-математические модели сочетают признаки дескриптивных и нормативных моделей. Типична ситуация, когда нормативная модель сложной структуры объединяет отдельные блоки, которые являются частными дескриптивными моделями. Например, межотраслевая модель может включать функции покупательского спроса, описывающие поведение потребителей при изменении доходов. Подобные примеры характеризуют тенденцию эффективного сочетания дескриптивного и нормативного подходов к моделированию экономических процессов. Дескриптивный подход широко применяется в имитационном моделировании.
По характеру отражения причинно-следственных связей различают модели жестко детерминистские и модели, учитывающие случайность и неопределенность. Необходимо различать неопределенность, описываемую вероятностными законами, и неопределенность, для описания которой законы теории вероятностей неприменимы. Второй тип неопределенности гораздо более сложен для моделирования.
По способам отражения фактора времени экономико-математические модели делятся на статические и динамические. В статических моделях все зависимости относятся к одному моменту или периоду времени. Динамические модели характеризуют изменения экономических процессов во времени. По длительности рассматриваемого периода времени различаются модели краткосрочного (до года), среднесрочного (до 5 лет), долгосрочного (10-15 и более лет) прогнозирования и планирования. Само время в экономико-математических моделях может изменяться либо непрерывно, либо дискретно.
Модели экономических процессов чрезвычайно разнообразны по форме математических зависимостей. Особенно важно выделить класс линейных моделей, наиболее удобных для анализа и вычислений и получивших вследствие этого большое распространение.
Различия между линейными и нелинейными моделями существенны не только с математической точки зрения, но и в теоретико-экономическом отношении, поскольку многие зависимости в экономике носят принципиально нелинейный характер: эффективность использования ресурсов при увеличении производства, изменение спроса и потребления населения при увеличении производства, изменение спроса и потребления населения при росте доходов и т.п. Теория “линейной экономики” существенно отличается от теории “нелинейной экономики”. От того, предполагаются ли множества производственных возможностей подсистем (отраслей, предприятий) выпуклыми или же невыпуклыми, существенно зависят выводы о возможности сочетания централизованного планирования и хозяйственной самостоятельности экономических подсистем.
По соотношению экзогенных и эндогенных переменных, включаемых в модель, они могут разделяться на открытые и закрытые. Полностью открытых моделей не существует; модель должна содержать хотя бы одну эндогенную переменную. Полностью закрытые экономико-математические модели, т.е. не включающие экзогенных переменных, исключительно редки; их построение требует полного абстрагирования от “среды”, т.е. серьезного огрубления реальных экономических систем, всегда имеющих внешние связи. Подавляющее большинство экономико-математических моделей занимает промежуточное положение и различаются по степени открытости (закрытости).
Для моделей народнохозяйственного уровня важно деление на агрегированные и детализированные.
В зависимости от того, включают ли народнохозяйственные модели пространственные факторы и условия или не включают, различают модели пространственные и точечные.
Таким образом, общая классификация экономико-математических моделей включает более десяти основных признаков. С развитием экономико-математических исследований проблема классификации применяемых моделей усложняется. Наряду с появлением новых типов моделей (особенно смешанных типов) и новых признаков их классификации осуществляется процесс интеграции моделей разных типов в более сложные модельные конструкции.
Основные этапы процесса моделирования уже рассматривались выше. В различных отраслях знаний, в том числе и в экономике, они приобретают свои специфические черты. Проанализируем последовательность и содержание этапов одного цикла экономико-математического моделирования.
1. Постановка экономической проблемы и ее качественный анализ. Главное здесь – четко сформулировать сущность проблемы, принимаемые допущения и те вопросы, на которые требуется получить ответы. Этот этап включает выделение важнейших черт и свойств моделируемого объекта и абстрагирование от второстепенных; изучение структуры объекта и основных зависимостей, связывающих его элементы; формулирование гипотез (хотя бы предварительных), объясняющих поведение и развитие объекта.
2. Построение математической модели. Это – этап формализации экономической проблемы, выражения ее в виде конкретных математических зависимостей и отношений (функций, уравнений, неравенств и т.д.). Обычно сначала определяется основная конструкция (тип) математической модели, а затем уточняются детали этой конструкции (конкретный перечень переменных и параметров, форма связей). Таким образом, построение модели подразделяется в свою очередь на несколько стадий.
Неправильно полагать, что чем больше фактов учитывает модель, тем она лучше “работает” и дает лучшие результаты. То же можно сказать о таких характеристиках сложности модели, как используемые формы математических зависимостей (линейные и нелинейные), учет факторов случайности и неопределенности и т.д.
Излишняя сложность и громоздкость модели затрудняют процесс исследования. Нужно учитывать не только реальные возможности информационного и математического обеспечения, но и сопоставлять затраты на моделирование с получаемым эффектом (при возрастании сложности модели прирост затрат может превысить прирост эффекта).
Одна из важных особенностей математических моделей – потенциальная возможность их использования для решения разнокачественных проблем. Поэтому, даже сталкиваясь с новой экономической задачей, не нужно стремиться “изобретать” модель; вначале необходимо попытаться применить для решения этой задачи уже известные модели.
В процессе построения модели осуществляется взаимосопоставление двух систем научных знаний – экономических и математических. Естественно стремиться к тому, чтобы получить модель, принадлежащую хорошо изученному классу математических задач. Часто это удается сделать путем некоторого упрощения исходных предпосылок модели, не искажающих существенных черт моделируемого объекта. Однако возможна и такая ситуация, когда формализация экономической проблемы приводит к неизвестной ранее математической структуре. Потребности экономической науки и практики в середине ХХ в. способствовали развитию математического программирования, теории игр, функционального анализа, вычислительной математики. Вполне вероятно, что в будущем развитие экономической науки станет важным стимулом для создания новых разделов математики.
3. Математический анализ модели. Целью этого этапа является выяснение общих свойств модели. Здесь применяются чисто математические приемы исследования. Наиболее важный момент – доказательство существования решений в сформулированной модели (теорема существования). Если удастся доказать, что математическая задача не имеет решения, то необходимость в последующей работе по первоначальному варианту модели отпадает и следует скорректировать либо постановку экономической задачи, либо способы ее математической формализации. При аналитическом исследовании модели выясняются такие вопросы, как, например, единственно ли решение, какие переменные (неизвестные) могут входить в решение, каковы будут соотношения между ними, в каких пределах и в зависимости от каких исходных условий они изменяются, каковы тенденции их изменения и т.д. Аналитической исследование модели по сравнению с эмпирическим (численным) имеет то преимущество, что получаемые выводы сохраняют свою силу при различных конкретных значениях внешних и внутренних параметров модели.
Знание общих свойств модели имеет столь важное значение, часто ради доказательства подобных свойств исследователи сознательно идут на идеализацию первоначальной модели. И все же модели сложных экономических объектов с большим трудом поддаются аналитическому исследованию. В тех случаях, когда аналитическими методами не удается выяснить общих свойств модели, а упрощения модели приводят к недопустимым результатам, переходят к численным методам исследования.
4. Подготовка исходной информации. Моделирование предъявляет жесткие требования к системе информации. В то же время реальные возможности получения информации ограничивают выбор моделей, предназначаемых для практического использования. При этом принимается во внимание не только принципиальная возможность подготовки информации (за определенные сроки), но и затраты на подготовку соответствующих информационных массивов.
Эти затраты не должны превышать эффект от использования дополнительной информации.
В процессе подготовки информации широко используются методы теории вероятностей, теоретической и математической статистики. При системном экономико-математическом моделировании исходная информация, используемая в одних моделях, является результатом функционирования других моделей.
5. Численное решение. Этот этап включает разработку алгоритмов для численного решения задачи, составления программ на ЭВМ и непосредственное проведение расчетов. Трудности этого этапа обусловлены, прежде всего, большой размерностью экономических задач, необходимостью обработки значительных массивов информации.
Обычно расчеты по экономико-математической модели носят многовариантный характер. Благодаря высокому быстродействию современных ЭВМ удается проводить многочисленные “модельные” эксперименты, изучая “поведение” модели при различных изменениях некоторых условий. Исследование, проводимое численными методами, может существенно дополнить результаты аналитического исследования, а для многих моделей оно является единственно осуществимым. Класс экономических задач, которые можно решать численными методами, значительно шире, чем класс задач, доступных аналитическому исследованию.
6. Анализ численных результатов и их применение. На этом заключительном этапе цикла встает вопрос о правильности и полноте результатов моделирования, о степени практической применимости последних.
Математические методы проверки могут выявлять некорректные построения модели и тем самым сужать класс потенциально правильных моделей. Неформальный анализ теоретических выводов и численных результатов, получаемых посредством модели, сопоставление их с имеющимися знаниями и фактами действительности также позволяют обнаруживать недостатки постановки экономической задачи, сконструированной математической модели, ее информационного и математического обеспечения.
Взаимосвязи этапов. На рис.1 изображены связи между этапами одного цикла экономико-математического моделирования.
Обратим внимание на возвратные связи этапов, возникающие вследствие того, что в процессе исследования обнаруживаются недостатки предшествующих этапов моделирования.
Уже на этапе построения модели может выясниться, что постановка задачи противоречива или приводит к слишком сложной математической модели. В соответствии с этим исходная постановка задачи корректируется. Далее математический анализ модели (этап 3) может показать, что небольшая модификация постановки задачи или ее формализации дает интересный аналитический результат.
Наиболее часто необходимость возврата к предшествующим этапам моделирования возникает при подготовке исходной информации (этап 4). Может обнаружиться, что необходимая информация отсутствует или же затраты на ее подготовку слишком велики. Тогда приходится возвращаться к постановке задачи и ее формализации, изменяя их так, чтобы приспособиться к имеющейся информации.
Поскольку экономико-математические задачи могут быть сложны по своей структуре, иметь большую размерность, то часто случается, что известные алгоритмы и программы для ЭВМ не позволяют решить задачу в первоначальном виде. Если невозможно в короткий срок разработать новые алгоритмы и программы, исходную постановку задачи и модель упрощают: снимают и объединяют условия, уменьшают число факторов, нелинейные соотношения заменяют линейными, усиливают детерминизм модели и т.д.
Недостатки, которые не удается исправить на промежуточных этапах моделирования, устраняются в последующих циклах. Но результаты каждого цикла имеют и вполне самостоятельное значение. Начав исследование с построения простой модели, можно быстро получить полезные результаты, а затем перейти к созданию более совершенной модели, дополняемой новыми условиями, включающей уточненные математические зависимости.
По мере развития и усложнения экономико-математического моделирования его отдельные этапы обособляются в специализированные области исследований, усиливаются различия между теоретико-аналитическими и прикладными моделями, происходит дифференциация моделей по уровням абстракции и идеализации.
Теория математического анализа моделей экономики развилась в особую ветвь современной математики – математическую экономику. Модели, изучаемые в рамках математической экономики, теряют непосредственную связь с экономической реальностью; они имеют дело с исключительно идеализированными экономическими объектами и ситуациями. При построении таких моделей главным принципом является не столько приближение к реальности, сколько получение возможно большего числа аналитических результатов посредством математических доказательств. Ценность этих моделей для экономической теории и практики состоит в том, что они служат теоретической базой для моделей прикладного типа.
Довольно самостоятельными областями исследований становятся подготовка и обработка экономической информации и разработка математического обеспечения экономических задач (создание баз данных и банков информации, программ автоматизированного построения моделей и программного сервиса для экономистов-пользователей). На этапе практического использования моделей ведущую роль должны играть специалисты в соответствующей области экономического анализа, планирования, управления. Главным участком работы экономистов-математиков остается постановка и формализация экономических задач и синтез процесса экономико-математического моделирования.
Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Воронежский государственный технический университет»
Кафедра экономической безопасности
МЕТОДЫ МОДЕЛИРОВАНИЯ БИЗНЕС-ПРОЦЕССОВ ПРЕДПРИЯТИЯ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ к изучению дисциплины, выполнению лабораторных работ и
самостоятельной работы для обучающихся по направлению 38.04.02 «Менеджмент»
(программамагистерской подготовки «Экономика и управление на предприятии») всех форм обучения
Воронеж 2021
УДК 658.5(07) ББК 65.290-21я7
Составитель
д-р экон. наук, проф. С.В. Амелин
Методы моделирования бизнес-процессов предприятия: методические указания по изучению дисциплины, выполнению лабораторных работ и самостоятельной работы для обучающихся по направлению 38.04.02 «Менеджмент» (программа магистерской подготовки «Экономика и управление на предприятии») всех форм обучения / ФГБОУ ВО «Воронежский государственный технический университет»; сост.: С. В. Амелин. – Воронеж: Изд-во ВГТУ, 2021. – 40 с.
Методические указания содержат теоретические сведения, необходимые для изучения ключевых понятий дисциплины, приобретения умений и навыков обоснования принятия решений посредством применения экономикоматематического моделирования бизнес-процессов в целях обеспечения и повышения эффективности деятельности предприятий и организаций.
Предназначены для магистрантов, обучающихся по направлению 38.04.02. «Менеджмент» (программа магистерской подготовки «Экономика и управление на предприятии») всех форм обучения.
Методические указания подготовлены в электронном виде и содержатся в файле МУ ММБП — 2021.pdf.
Ил. 7. Табл. 4. Библиогр.: 6 назв.
УДК 658.5(07) ББК 65.290-21я7
Рецензент — И. Ф. Елфимова, канд. экон. наук, доц. кафедры экономической безопасности ВГТУ
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
2
ВВЕДЕНИЕ
Целью изучения дисциплины является формирование у обучающихся в магистратуре комплекса знаний, умений и практических навыков использования современной теории и практики экономико-математического моделирования бизнес-процессов предприятия.
Задачами дисциплины «Методы моделирования бизнес-процессов предприятия» являются:
—изучение теоретических основ и развитие практических навыков применения математического аппарата методов экономико-математического моделирования бизнес-процессов предприятия с использованием современных информационных технологий;
—освоение будущим магистром методов поиска и обоснованного выбора наилучших организационно-экономических решений с использованием методов системного анализа;
—развитие навыков использования методов оптимизации в процессе математического моделирования бизнес-процессов предприятия.
Результатом изучения дисциплины «Методы моделирования бизнеспроцессов предприятия» является освоение компетенций:
ПК-3 — Способен применять математический аппарат, методы оптимизации, системного анализа для принятия решений в области стратегического и тактического планирования организации производства.
Методические указания включают содержание тем изучаемой дисциплины в соответствии с рабочей программой, перечень лабораторных работ, рекомендации по выполнению самостоятельной работы, а также перечень рекомендуемой литературы и вопросы к экзамену и задания для самопроверки.
1.МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ИЗУЧЕНИЮ ДИСЦИПЛИНЫ
Тема 1. Методы моделирования бизнес-процессов
Методологические основы моделирования производственно-экономических систем и бизнес-процессов. Процесс системного моделирования производственных систем и процессов. Математическое моделирование в экономике. Этапы экономико-математического моделирования. Постановка экономической проблемы и ее качественный анализ. Построение математической модели. Математический анализ модели. Подготовка исходной информации. Численное решение. Анализ численных результатов и их применение.
Тема 2. Классификация моделей производственных систем и бизнеспроцессов
Материальные модели и абстрактные. Модели производственноэкономических систем, региональных комплексов, отраслевые модели, модели народного хозяйства. Модели перспективного, стратегического планирования, текущего и оперативно-календарного. Модели линейные и нелинейные. Модели детерминированные и стохастические. Модели статические и динамические. Ими-
3
тационные модели. Эвристические методы в моделировании. Графические модели. Элементы теории графов.
Тема 3.Системный подход к производству, как объекту моделирования
Понятие системы. Большие сложные системы. Производственноэкономические системы. Иерархические системы. Свойство эмерджентности. Целенаправленность систем. Процессы передачи информации и управления в сложно организованных системах. Понятие цели. Классификация целей. Дерево целей. Требования к компонентам сложных систем. Понятие обратной связи. Моделирование обратных связей. Метод анализа иерархий.
Тема 4. Моделирование структур производственных систем
Функциональное, морфологическое и информационное описание систем. Понятие структуры. Организационная структура, функциональная, техническая. Моделирование структур. Типы организационных структур и их модели. Последовательная структура, кольцевая, звездочная, многосвязная, иерархическая, смешанная. Количественные параметры моделей организационных структур. Критерий оптимальности. Моделирование структур производственных систем на основе теории графов. Матричное моделирование структур производственных систем. Информационный подход в моделировании сложных производственно-экономических систем. Энтропийные методы моделирования производственных систем.
Тема 5. Методы отбора существенных факторов моделей
Использование методов экспертного опроса и статистического анализа. Этапы процедуры экспертного исследования. Формирование списка факторов моделей исследователем. Подготовка анкеты. Формирование группы экспертов. Постановка задачи экспертам. Проведение опроса экспертов. Составление сводной таблицы результатов опроса. Ранжирование оценок экспертов. Оценка согласованности мнений экспертов. Оценка статистической значимости коэффициента конкордации. Отыскание параметров эмпирических математических моделей производственно-экономических систем. Моделирование с использованием метода «черного ящика». Понятие об интерполяции, аппроксимации и экстраполяции. Экономико-математические модели для аппроксимации опытных данных. Метод наименьших квадратов. Корреляционно-регрессионный анализ.
Тема 6. Имитационное моделирование
Имитационное моделирование как метод исследования и анализа производственно-экономических систем и процессов. Аналитическое и имитационное моделирование. Случаи использования имитационного моделирования. Классификация имитационных моделей. Порядок построения имитационной модели производственно-экономической системы и проведения машинных имитационных экспериментов. Планирование эксперимента.. Полный и неполный факторный эксперимент.
4
2. МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ПРОВЕДЕНИЮ ЛАБОРАТОРНЫХ РАБОТ
Методические указания к проведению лабораторных работ представлены в пособии 3.65(ББК) А 615 Амелин, С.В. Методы моделирования управленческих, экономических и бизнес-процессов [Электронный ресурс] : Лабораторный практикум: Учеб. пособие. — Электрон. текстовые, граф. дан. ( 1,83 Мб ). — Воронеж : ФГБОУ ВПО «Воронежский государственный технический универ-
ситет», 2015. — 1 файл. — 30-00. http://bibl.cchgeu.ru/MarcWeb2/Found.asp
Перечень лабораторных работ
Лабораторная работа № 1 .Моделирование бизнес-процессов массового обслуживания. Система обслуживания с одним прибором и очередью
Лабораторная работа № 2. Отбор существенных факторов моделей про- изводственно-экономических систем с помощью методов экспертного опроса, статистического анализа, оптимизационных моделей
Лабораторная работа № 3. Моделирование многоканальных систем массового обслуживания. Моделирование работы банковского учреждения
Лабораторная работа № 4. Моделирование многоканальных систем массового обслуживания. Моделирование работы подразделения предприятия — фирменного торгового дома
Лабораторная работа № 5. Моделирование действия производственноэкономической системы в условиях рыночной ситуации с использованием игровых моделей теории игр.
Лабораторная работа № 6. Методы поиска решений с помощью имитационной модели участка производства. Имитационное моделирование процессов контроля на участке производства.
Отчёты по лабораторным работам оформляются индивидуально на листах формата А4 с титульным листом и подписью. Отчёты должны включать: цель и задачи лабораторной работы, краткие исходные положения, исходные данные для расчёта, расчётные формулы, скриншоты расчётов на компьютере, анализ полученных результатов и выводы. Все таблицы и иллюстрации должны иметь названия.
3. МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Рабочей программой дисциплины «Методы моделирования бизнеспроцессов предприятия» предусмотрена самостоятельная работа студентов.
5
Виды самостоятельной работы:
1.Подготовка к лекциям и самостоятельная проработка материала;
2.Подготовка к лабораторным занятиям;
3. Самоподготовка к итоговой проверке знаний;
Подготовка к лекциям и самостоятельная проработка материала яв-
ляется обязательным видом самостоятельной работы и предполагает предварительное ознакомление студента с вопросами предстоящей лекции с целью наиболее эффективного усвоения материала. Особое внимание следует уделить вопросам, выносимым на самостоятельное изучение.
Подготовка к лабораторным занятиям заключается в проработке теоре-
тического материала к каждой лабораторной работе. Защита лабораторных работ является обязательной и оценивается преподавателем как элемент общей успеваемости студента.
Отчёты по лабораторным работам оформляются как индивидуальный отчет студента, на листах формата А4 в соответствии с требованиями нормокнтроля ВГТУ. Наличие титульного листа обязательно.
Самоподготовка к итоговой проверке знаний предполагает самостоя-
тельную проработку материала, опираясь на содержание лекций и практических занятий, вопросы, выносимые на самостоятельное изучение.
Студент допускается к итоговой аттестации (экзамену) на основании посещения лекций, а также выполнения лабораторных работ. На экзамен выносятся основные вопросы, изучаемые в течение семестра. Экзамен предполагает ответы на теоретические вопросы, выполнение стандартного и прикладного задания.
ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Выбор вариантов каждой части задания производится преподавателем согласно спискам студентов по группам.
ЗАДАНИЕ № 1 МОДЕЛИРОВАНИЕ СТРУКТУР ПРОИЗВОДСТВЕННЫХ СИСТЕМ
При изучении методов моделирования структур производственных систем необходимо рассмотреть следующие вопросы: определение основных структурных характеристик; определение структурных параметров органов управления организации. При этом можно использовать следующую информацию.
Моделирование формальной структуры ПС включает сбор информации, характеризующий её в статике (тип организационной структуры, распределение прав и обязанностей и т.п.), и изучение её в динамике (определение эффективности организационной структуры с позиций достижения конечных результатов деятельности).
6
При моделировании организационной структуры большое значение имеет фиксирование формальных каналов коммуникаций, которые представляют интерес для рационального распределения функций и обязанностей в ходе подготовки и принятия решений. Необходимо изучать также неформальную структуру ПС. Сбор информации для моделирования ведется посредством наблюдения за групповыми и межличностными отношениями и их изменениями, проведения серий интервью, что дает возможность определить моральнопсихологический климат на предприятии.
Информация собирается по подразделениям, отделам, у должностных лиц предприятия,- об их взаимодействии между собой, способах принятия и выполнения решений, их деятельность по обеспечению работоспособности предприятия. Информация для данной работы относится к «внутреннему» типу. Ее получение возможно частично из документов предприятия, а частично — в беседе с сотрудниками.
Моделирование позволяет определять некоторые характеристики структуры ПС и давать им количественную оценку, оценивать качество структуры ПС и её элементов с позиций системного анализа, а также сравнивать различные варианты организационных структур между собой.
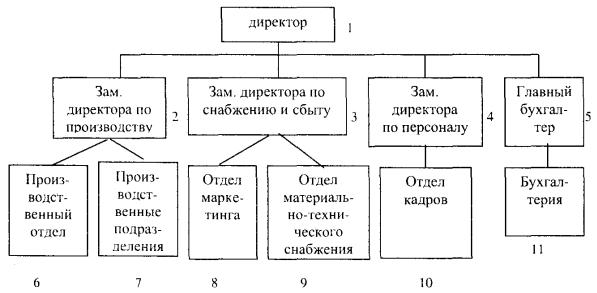
Рассмотрим, например, линейно-функциональную структуру управления, в которой каждый структурный элемент (отдел, служба, производственное подразделение) выполняет конкретные задачи и обладает определенными правами и обязанностями.
Рис. 1. Организационная структура предприятия
Для проведения структурного анализа организационной структуры предприятия представим ее в виде графа G = {Х, U}, где Х — множество вершин (|Х| = n), соответствующее множеству структурных элементов; U — множество рёбер
7
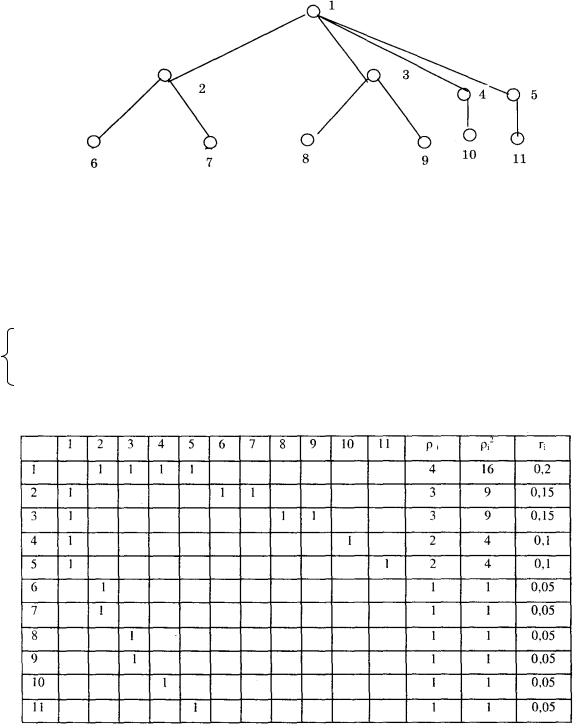
(|U| = m), соответствующее множеству связей между структурными элементами предприятия.
Граф G, соответствующий данному предприятию, показан на рис. 5, где цифры обозначают: 1 — директор предприятия; 2 — зам. директора по производству; 3 — зам. директора по снабжению и сбыту; 4 — зам. директора по персоналу; 5 — главный бухгалтер; 6 — производственный отдел; 7 — производственные подразделения; 8 — отдел маркетинга; 9 — отдел материально-технического снабжения; 10 — отдел кадров; 11 — бухгалтерия.
Рис. 2. Структурный граф предприятия
Для описания графа G построим матрицу смежности (табл. 1), которая для неориентированного графа имеет вид А = ||аij||, где аij — элементы матрицы смежности, определяемые следующим образом:
1 — при наличии связи между элементами i и j,
аij =
0 — при отсутствии связи.
Таблица 1
Матрица смежности
8
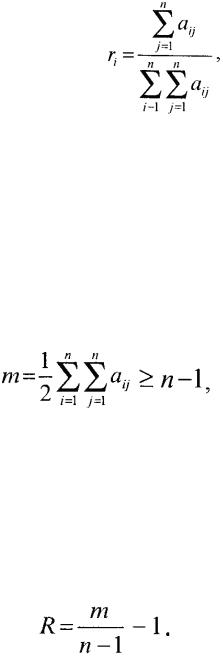
1. По матрице смежности определим ранг каждого элемента
(1)
где aij – элементы матрицы смежности, n – количество вершин (элементов) структуры.
Например, r1 = 4 ∕ 20 = 0,2. Ранги структурных элементов приведены в последнем столбце табл. 1.
Чем выше ранг элемента, тем более сильно он связан с другими элементами и тем более тяжёлыми будут последствия при потере качества его функционирования. В рассматриваемом случае наиболее высокий ранг (0,2) имеет первый элемент структуры (директор).
2. Проверим связность структуры. Для связных структур (не имеющих обрывов и висячих элементов) должно выполняться условие
(2)
гдеm – множество рёбер графа (½ отколичества связей в матрице смежности). Правая часть неравенства определяет необходимое минимальное число
связей в структуре графа, содержащего n вершин.
Для нашего случая n (количество структурных элементов) равно 11 и условие (½)·20 = 11–1 выполняется, т.е. структура является связной.
3. Проведем оценку структурной избыточности R, отражающей превышение общего числа связей над минимально необходимым:
(3)
Данная характеристика является косвенной оценкой экономичности и надёжности исследуемой структуры и определяет принципиальную возможность функционирования и сохранения связей системы при отказе некоторых её элементов. Система с большей избыточностью R потенциально более надёжна, но менее экономична. Возможны три варианта: если R<0, то система несвязная; R = 0, система обладает минимальной избыточностью; R > 0, система имеет избыточность; чем выше R, тем выше избыточность.
Для рассматриваемого случая R = [(½)·20∕ (11–1)] – 1 = 0, т.е. структура имеет минимальную избыточность.
9

4. Определим неравномерность распределения связей — Е. Данный показатель характеризует недоиспользование возможностей данной структуры, имеющей m рёбер и n вершин, в достижении максимальной связности. Величина Е определяется по формуле
(4)
— вес i-го элемента, или количество связей i— го элемента со
всеми остальными.
Для рассматриваемого случая Е = 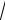
Однако для сравнения различных структур по неравномерности связей используют относительную величину
где Еmах — максимальное значение неравномерности связей, которое достигается в системе, имеющей максимально возможное число вершин, имеющих одну связь.
Величину Е определяют по эмпирической формуле
(6)
где y = m – n ; x = ( −1 + 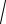
Для рассматриваемого случая
y = 10 – 11 = –1; х = ( −1 + 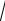
Тогда
Определим величину Е для рассматриваемого случая.
Еотн = 3,41 ∕ 8,58 = 0,4.
10
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #



