Двое рабочих работая вместе могут выполнить работу за 6 часов за сколько дней работая отдельно

Типичные задачи на совместную работу в 6 классе

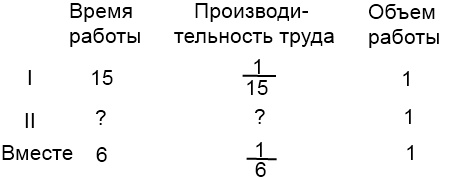
1) Двое рабочих, работая вместе, выполняют некоторую работу за 6 часов. Один из них, работая самостоятельно, может выполнить эту работу за 15 часов. За сколько часов может выполнить эту работу другой рабочий?

В отличие от всех других типов задач, задачи на совместную работу начинаются с того, что всю работу (все задание, весь бассейн, все поле — то, о чем идет речь в задаче) принимаем за единицу. То есть объем работы в этом случае равен единице. Чтобы найти объем работы, надо производительность труда умножить на время работы. Соответственно, чтобы найти производительность труда (часть работы, выполненную за определенную единицу времени), надо объем работы разделить на время работы: 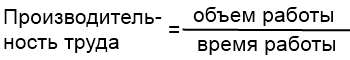Решение задач на совместную работу упрощается, если условие оформить в виде таблицы.

Перейдем с решению нашей задачи.

Решение.

Примем всю работу за 1.

Чтобы найти производительность труда второго рабочего, из производительности труда совместной работы вычтем производительность труда первого рабочего:

$[1)frac{{{1^{backslash 5}}}}{6} - {frac{1}{{15}}^{backslash 2}} = frac{{5 - 2}}{{30}} = frac{3}{{30}} = frac{1}{{10}}]$

Такую часть работы в 1 час выполняет второй рабочий.

Зная производительность труда второго рабочего и объем работы, можем найти время, за которое он может выполнить работу самостоятельно. Чтобы найти время работы, надо объем работы разделить на производительность труда:

$[2)1:frac{1}{{10}} = 1 cdot frac{{10}}{1} = 10]$

Значит, второй рабочий, работая отдельно, может выполнить работу за 10 часов.

Ответ: за 10 часов.

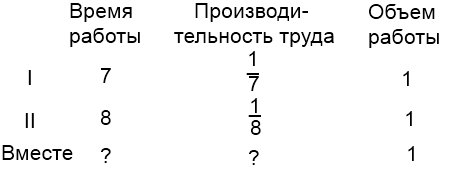
2) Через одну трубу бассейн наполняется за 7 часов, а через другую опустошается за 8 часов. За какое время бассейн будет наполнен, если открыть обе трубы?

Решение.

Примем весь бассейн за 1.

Сначала найдем производительность труда совместной работы обеих труб за один час. Поскольку одна труба бассейн наполняет, а другая — опустошает, производительность совместной работы равна разности производительности первой и второй труб:

$[1)frac{{{1^{backslash 8}}}}{7} - frac{{{1^{backslash 7}}}}{8} = frac{{8 - 7}}{{56}} = frac{1}{{56}}]$

Теперь найдем время, за которое бассейн будет наполнен при открытии обеих труб одновременно. Чтобы найти время работы, надо объем работы разделить на производительность труда:

$[2)1:frac{1}{{56}} = 1 cdot frac{{56}}{1} = 56]$

Таким образом, за 56 часов совместной работы обеих труб бассейн будет наполнен.

Ответ: за 56 часов.

Источник

Двое рабочих работая вместе, могут выполнить некоторую работу за 6 ч. Один из них, работая самостоятельно, может выполнить эту работу за 15 ч. За сколько часов ее может выполнить самостоятельно другой рабочий?

reshalka.com

Математика 6 класс Мерзляк. Номер №480

Решение

6
15

2
5

работы выполнит первый рабочий.

1
−

2
5

3
5

работы выполнит второй рабочий.

3
5

:
6
=

3
5

∗

1
6

1
5

∗

1
2

1
10

часть работы выполнит второй рабочий за 1 час.

1
:

1
10

=
1
∗
10
=
10

часов потребуется на выполнение работы второму рабочему.

Источник

Двое рабочих, работая вместе, могут выполнить работу за 6 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за 3 дня выполняет такую же часть работы, какую второй — за 2 дня?

Помогите пж пж пж пж

Светило науки — 21802 ответа — 3957 раз оказано помощи

Ответ:

15 дней

Пошаговое объяснение:

Вся работа = 1

Производительность 1 рабочего в день = х

Производительность 2 рабочего в день = у

6х + 6у = 1

3х = 2у

6х + 6у = 1

3х — 2у = 0 | * 3

6х + 6у = 1

9х — 6у = 0

15х = 1

6х + 6у = 1

15х = 1

х = 1 : 15

х = 1/15

6х + 6у = 1

6 * 1/15 + 6у = 1

6/15 + 6у = 1

6у = 1 — 6/15

6у = 9/15

у = 9/15 : 6

у = 9/15 * 1/6

у = 3/15 * 1/2

у = 3/30

у = 1/10

Производительность 1 рабочего в день = (х) = 1/15

Производительность 2 рабочего в день = (у) = 1/10

1 : 1/15 = 1 * 15/1 = 15/1 = 15 (дней) — выполнит работу 1 рабочий работая отдельно

1 : 1/10 = 1 * 10/1 = 10/1 = 10 (дней) — выполнит работу 2 рабочий работая отдельно

Ответ: за 15 дней

Остались вопросы?

Новые вопросы по предмету Математика

Источник