Двое рабочих могут выполнить заказ за 6 часов после трех часов совместной работы

1. Два мастера, работая вместе, могут выполнить заказ за 6 ч. Если первый мастер будет работать 9 ч, а потом его сменит второй, то он закончит работу через 4 ч. За сколько времени может выполнить заказ каждый из мастеров, работая отдельно?

Комментариев (0)

Пусть х — скорость работы первого мастера, а y — скорость работы второго мастера и 1 — вся работа.
Решаем по формуле:

$t=frac{A}{v}$

t — время.

A — работа.

v — скорость.

$left { {{frac{1}{(x+y)=6}} atop {9x+4y=1}} right.$

$left { {{x+y=frac{1}{6}} atop {9x+4y=1}} right.$

$left { {{x=frac{1}{6}-y} atop {frac{3}{2}-9y+4y=1}} right.$

$left { {{x=frac{1}{6}-y} atop {5y=frac{1}{2}}} right.$

1) x=1/15 — скорость работы первого мастера.
2) y=1/10 — скорость работы второго мастера.

3) 1/x=15(часов) — время работы первого мастера.
4) 1/y=10(часов) — время работы второго мастера.

Ответ: первый мастер выполнит работу за 15 часов, а второй за 10 часов.

Комментариев (0)

Источник

Каждый из двух рабочих

Дата: 2015-03-20

14730

Категория: Работа

Метка: ЕГЭ-№9

99613. Каждый из двух рабочих одинаковой квалификации может выполнить заказ за 15 часов. Через 3 часа после того, как один из них приступил к выполнению заказа, к нему присоединился второй рабочий, и работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение всего заказа?

Отметим, что производительность каждого рабочего равна 1/15 (заказа в час). Заказ это вся работа, в данном случае она равна 1. Пусть х это время совместной работы. Тогда получается, что один работал х часов, а другой х+3 часов.

Заполним графу «работа» для каждого:

Сумма сделанных ими объёмов работы составляет всю работу (она как уже отметили равна единице), можем записать:

Совместно рабочие работали только 6 часов.

Таким образом на весь заказ ушло 6+3=9

Второй подход к решению

В условии сказано, что рабочий может выполнить заказ за 15 часов, то есть его производительность равна 1/15 заказа в час.

Значит за первые три часа один рабочий выполнит 3/15 заказа.

Получается, что на двоих останется:

Далее они работают вдвоём, значит на каждого из рабочих придётся по:

так как их производительность одинаковая.

Известно, что рабочий выполняет 1/15 заказа в час, значит 6/15 заказа он выполнит за 6 часов, то есть совместно они будут работать только 6 часов. Таким образом, на выполнение всего заказа потребуется 6+3=9 часов

Ответ: 9

Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.

Источник

Двое рабочих работая вместе, могут выполнить некоторую работу за 6 ч. Один из них, работая самостоятельно, может выполнить эту работу за 15 ч. За сколько часов ее может выполнить самостоятельно другой рабочий?

reshalka.com

Математика 6 класс Мерзляк. Номер №480

Решение

6
15

2
5

работы выполнит первый рабочий.

1
−

2
5

3
5

работы выполнит второй рабочий.

3
5

:
6
=

3
5

∗

1
6

1
5

∗

1
2

1
10

часть работы выполнит второй рабочий за 1 час.

1
:

1
10

=
1
∗
10
=
10

часов потребуется на выполнение работы второму рабочему.

Источник

Типичные задачи на совместную работу в 6 классе

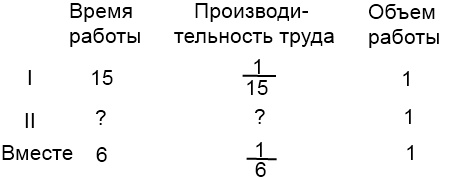
1) Двое рабочих, работая вместе, выполняют некоторую работу за 6 часов. Один из них, работая самостоятельно, может выполнить эту работу за 15 часов. За сколько часов может выполнить эту работу другой рабочий?

В отличие от всех других типов задач, задачи на совместную работу начинаются с того, что всю работу (все задание, весь бассейн, все поле — то, о чем идет речь в задаче) принимаем за единицу. То есть объем работы в этом случае равен единице. Чтобы найти объем работы, надо производительность труда умножить на время работы. Соответственно, чтобы найти производительность труда (часть работы, выполненную за определенную единицу времени), надо объем работы разделить на время работы: 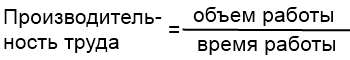Решение задач на совместную работу упрощается, если условие оформить в виде таблицы.

Перейдем с решению нашей задачи.

Решение.

Примем всю работу за 1.

Чтобы найти производительность труда второго рабочего, из производительности труда совместной работы вычтем производительность труда первого рабочего:

$[1)frac{{{1^{backslash 5}}}}{6} - {frac{1}{{15}}^{backslash 2}} = frac{{5 - 2}}{{30}} = frac{3}{{30}} = frac{1}{{10}}]$

Такую часть работы в 1 час выполняет второй рабочий.

Зная производительность труда второго рабочего и объем работы, можем найти время, за которое он может выполнить работу самостоятельно. Чтобы найти время работы, надо объем работы разделить на производительность труда:

$[2)1:frac{1}{{10}} = 1 cdot frac{{10}}{1} = 10]$

Значит, второй рабочий, работая отдельно, может выполнить работу за 10 часов.

Ответ: за 10 часов.

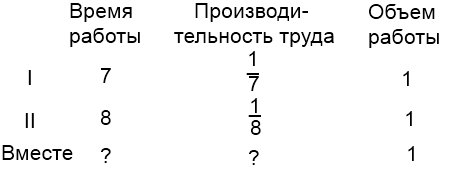
2) Через одну трубу бассейн наполняется за 7 часов, а через другую опустошается за 8 часов. За какое время бассейн будет наполнен, если открыть обе трубы?

Решение.

Примем весь бассейн за 1.

Сначала найдем производительность труда совместной работы обеих труб за один час. Поскольку одна труба бассейн наполняет, а другая — опустошает, производительность совместной работы равна разности производительности первой и второй труб:

$[1)frac{{{1^{backslash 8}}}}{7} - frac{{{1^{backslash 7}}}}{8} = frac{{8 - 7}}{{56}} = frac{1}{{56}}]$

Теперь найдем время, за которое бассейн будет наполнен при открытии обеих труб одновременно. Чтобы найти время работы, надо объем работы разделить на производительность труда:

$[2)1:frac{1}{{56}} = 1 cdot frac{{56}}{1} = 56]$

Таким образом, за 56 часов совместной работы обеих труб бассейн будет наполнен.

Ответ: за 56 часов.

Источник