Для нагревательного прибора экспериментально была получена зависимость температуры от времени работы

Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в кельвинах) от времени работы: T(t) = T₀ + bt + at² , где t  — время в минутах, T₀ = 1380 К, а = −15 К/мин², b= 165 К/мин. Известно, что при температуре нагревателя свыше 1800 К прибор может испортиться, поэтому его нужно отключить. Определите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ выразите в минутах.

Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в кельвинах) от времени работы:где t  — время (в мин.), T₀  =  680 К, а  =  −16 К/мин², b  =  224 К/мин. Известно, что при температуре нагревательного элемента свыше 1400 К прибор может испортиться, поэтому его нужно отключить. Найдите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ дайте в минутах.

Источник: ЕГЭ — 2016. Основная волна по математике 06.06.2016. Вариант 437. Юг

Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в К) от времени работы:

где t  — время (в мин.), T₀ = 1380 К, a = −15 К/мин², b = 165 К/мин. Известно, что при температуре нагревательного элемента свыше 1800 К прибор может испортиться, поэтому его нужно отключить. Найдите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ дайте в минутах.

Источник: ЕГЭ по математике 31.03.2017. Досрочная волна.

Источник

Задание 10. Математика ЕГЭ. Найдите, через какое наибольшее время после начала работы нужно отключить прибор.

Задание. Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в К) от времени работы:

T(t) = T₀ + bt + αt²,

где t – время (в мин.), T₀ = 1600 К, α = – 5 К/мин², b = 105 К/мин. Известно, что при температуре нагревательного элемента свыше 1870 К прибор может испортиться, поэтому его нужно отключить. Найдите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ дайте в минутах.

Решение:

По условию задачи T₀ = 1600 К, α = – 5 К/мин², b = 105 К/мин, T(t) = 1870 К.

Подставим числовые значения в формулу T(t) = T₀ + bt + αt², получим

1870 = 1600 + 105t – 5t²

5t² – 105t + 270 = 0

D = 75

t₁ = 3 и t₂ = 18

Следовательно, t = 3 мин – это наибольшее время после начала работы, когда нужно отключить прибор, так как превышение этого времени приведет к его поломку. А второй раз через 18 мин прибор не сможет сломаться.

Ответ: 3

Оставить комментарий

Рубрики

Демоверсия ЕГЭ по информатике
Демоверсия ЕГЭ по математике
Демоверсия ОГЭ по информатике
Демоверсия ОГЭ по математике
Материалы по аттестации
Решаем ЕГЭ по математике
- Задание 1
- Задание 10
- Задание 11
- Задание 12
- Задание 13
- Задание 14
- Задание 15
- Задание 16
- Задание 2
- Задание 3
- Задание 4
- Задание 5
- Задание 6
- Задание 7
- Задание 8
- Задание 9
Решаем ОГЭ по математике
- Задание 21
- Задание 22
- Задание 24
Скачать экзаменационные варианты по информатике
- ЕГЭ по информатике
- ОГЭ по информатике
Скачать экзаменационные варианты по математике
- ЕГЭ по математике
- ОГЭ по математике
Тематическое планирование

Источник

Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в Кельвинах) от времени работы: T(t) = T₀ + bt + at², где t – время в минутах, Т₀ = 1600 К, а = –5 К/мин², b = 105 К/мин. Известно, что при температуре нагревательного элемента свыше 1870 К прибор может испортиться, поэтому его нужно отключить. Найдите, через какое наименьшее время после начала работы нужно отключить прибор. Ответ дайте в минутах.

Источники: fipi, os.fipi

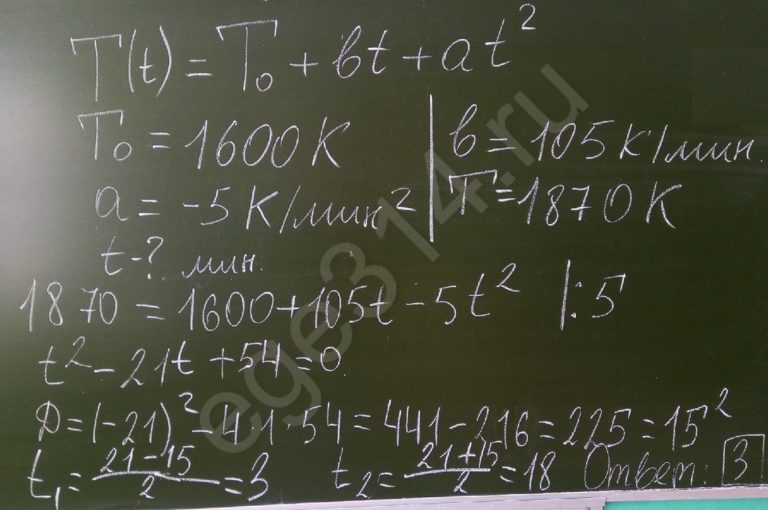
Через 3 минуты прибор нагреется до максимума, и его надо будет отключить, к 18 минутам прибор сгорит.

Ответ: 3.

Задание с похожим выбором ответа здесь.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4 / 5. Количество оценок: 1

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник

10. Задачи прикладного характера

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Основные способы решения некоторых простейших неравенств:

1. Квадратичное неравенство (ax^2+bx+c> 0). Если уравнение (ax^2+bx+c=0) имеет корни (x_1, x_2) (или один корень (x_1)), его можно переписать в виде (a(x-x_1)(x-x_2)>0) ((a(x-x_1)^2>0)) и далее решить методом интервалов.
Если уравнение не имеет корней, то при (a>0) выражение (ax^2+bx+c>0), при (a<0) выражение (ax^2+bx+c<0) при всех (x).

2. Показательное неравенство (a^{f(x)}> a^{g(x)}) равносильно (f>g), если (a>1), или (f<g), если (0<a<1).

3. Логарифмическое неравенство (log_a{f(x)}> log_a{g(x)}) равносильно (f>g), если (a>1), или (f<g), если (0<a<1), при условии выполненного ОДЗ: (f>0, g>0).

Задание
29

#1340

Уровень задания: Сложнее ЕГЭ

Азат толкнул ядро под углом (phi) к горизонтальной поверхности земли. Продолжительность полета ядра в секундах можно найти по формуле [t = dfrac{2v_0sin{phi}}{g}.] При каком наибольшем значении угла (phi) в градусах время полета ядра будет не менее, чем (1,2) секунды, если Азат толкнул его с начальной скоростью (v_0 = 12) м/с? Считайте, что ускорение свободного падения (g = 10) м/с(^2).

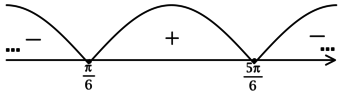
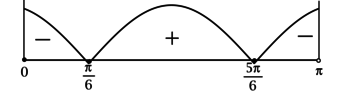
[1,2 leq t = dfrac{2cdot 12cdot sin phi}{10} qquadLeftrightarrowqquadsin phi geq 0,5.] Решим неравенство (sin phi geq 0,5) методом интервалов. Найдем корни уравнения (sin phi = 0,5): [phi = dfrac{pi}{6} + pi k,qquadqquad phi = dfrac{5pi}{6} + pi k,] где (k in mathbb{Z}). Тогда:

здесь бесконечно много интервалов, но знаки в них чередуются. Кроме того, (phi in [0; pi)), тогда:

тогда (phi in left[dfrac{pi}{6}; dfrac{5pi}{6}right]) и наибольшее подходящее значение (phi) равно (dfrac{5pi}{6}), то есть (150^{circ}).

Ответ: 150

Задание
30

#1332

Уровень задания: Сложнее ЕГЭ

Маша подбросила мячик, высота которого до падения меняется по закону (h = 1 + 7t — 5t^2), где (h) – высота в метрах, (t) – время в секундах, отсчитываемое от момента подбрасывания. Сколько секунд с момента подбрасывания мячик находился на высоте не менее (1) метра, но не более (2,2) метров?

Моменты (t), в которые мячик находился на высоте не менее (1) метра, но не более (2,2) метров удовлетворяют двойному неравенству [1 leq 1 + 7t — 5t^2 leq 2,2.] Решим два неравенства по очереди.

Рассмотрим неравенство (1 leq 1 + 7t — 5t^2). Оно равносильно неравенству [5t^2 — 7t leq 0,] которое решим методом интервалов. Найдём корни уравнения (5t^2 — 7t = 0): [t_1 = 0, qquadqquad t_2 = 1,4,] тогда:

тогда решениями этого неравенства будут (tin[0; 1,4]).

Рассмотрим теперь неравенство (1 + 7t — 5t^2 leq 2,2). Оно равносильно неравенству [5t^2 -7t + 1,2 geq 0,] которое решим методом интервалов. Найдём корни уравнения (5t^2 -7t + 1,2 = 0): [t_1 = 0,2, qquadqquad t_2 = 1,2,] тогда:

но с учётом того, что (t geq 0) подходят только (tin[0; 0,2] cup [1,2; +infty)).

В итоге мячик находился на высоте не менее (1) метра, но не более (2,2) метров в моменты (tin[0; 0,2] cup [1,2; 1,4]), то есть в течение ((0,2 — 0) + (1,4 — 1,2) = 0,4) секунды.

Ответ: 0,4

Задание
31

#1331

Уровень задания: Сложнее ЕГЭ

Подводная лодка “Скумбрия”( )плывет с постоянной скоростью (v_0 = 20) узлов (1 узел = 1 морская миля в час). В момент времени (t = 0) часов она выпускает торпеду, которая до попадания в цель разгоняется с постоянным ускорением (a = 80) узлов в час. Расстояние в морских милях от места пуска до торпеды определяется из формулы [S = v_0t+dfrac{at^2}{2}.] Определите в течение какого времени с момента пуска торпеда плыла последние (1,3) морской мили до цели, если в момент пуска расстояние до неподвижной цели было 2,4 морских мили. Ответ дайте в часах.

Разделим путь торпеды на 2 участка: участок А – первые 1,1 морской мили пути; участок В – последние 1,3 морской мили пути. Тогда моменты (t), в которые торпеда будет находиться на участке В, удовлетворяют двойному неравенству [1,1 leq 20t + 40t^2 leq 2,4.] Решим два неравенства по очереди.

Рассмотрим неравенство (1,1 leq 20t + 40t^2). Оно равносильно неравенству [40t^2 + 20t — 1,1 geq 0,] которое решим методом интервалов. Найдём корни уравнения (20t + 40t^2 — 1,1 = 0): [t_1 = -0,55,qquadqquad t_2 = 0,05,] тогда:

но с учётом того, что (t geq 0) подходят только (t geq 0,05).

Рассмотрим теперь неравенство (20t + 40t^2 leq 2,4). Оно равносильно неравенству [40t^2 + 20t — 2,4 leq 0,] которое решим методом интервалов. Найдём корни уравнения (20t + 40t^2 — 2,4 = 0): [t_1 = -0,6,qquadqquad t_2 = 0,1,] тогда:

но с учётом того, что (t geq 0) подходят только (0 leq t leq 0,1).

В итоге торпеда находилась на участке В в моменты (0,05 leq t leq 0,1), то есть в течение (0,1 — 0,05 = 0,05) часа.

Ответ: 0,05

Задание
32

#4024

Уровень задания: Легче ЕГЭ

Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в кельвинах) от времени работы: [T(t)=T_0+bt+at^2,]где (t) – время в минутах, (T_0=1300) К, (a=-dfrac{14}3) К/мин(^2), (b=98) К/мин.
Известно, что при температуре нагревательного элемента свыше (1720) К прибор может испортиться, поэтому его нужно отключить. Найдите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ дайте в минутах.

Из условия задачи следует, что (T(t)) должно быть не больше (1720), то есть, подставляя все данные из условия, получим следующее неравенство [1300+98t-dfrac{14}3t^2leqslant 1720 Big|cdot
left(-dfrac3{14}right) quadLeftrightarrowquad
t^2-21t+90geqslant 0] Корнями многочлена (t^2-21t+90) являются (t=6) и (t=15). Следовательно, решением неравенства будут (tin (-infty;6]cup[15;+infty)).

Таким образом, наибольшее время, после которого нужно отключить прибор, равно (6) (мин).
Из решения неравенства следует, что после 6-ой минуты температура нагревательного элемента превысит 1720 К, то есть после 6-ой минуты нагревательный элемент уже испортился ! Именно поэтому мы выбираем ответ 6 минут.

Ответ:

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в кельвинах)

Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в кельвинах) от времени работы: T(t) = T0+bt+at², где t — время в минутах, a = — 10 К/мин², b = 100 К/мин. Известно, что при температуре нагревателя свыше 1700 К прибор может испортиться, поэтому его нужно отключить. Найдите наибольшую возможную начальную температуру необходимую для работы прибора не менее 8 минут. Ответ дайте в К.

Источник

Зависимость температуры (в градусах Кельвина)

Дата: 2014-09-29

6876

Категория: Физические задачи

Метка: ЕГЭ-№8

27962. Зависимость температуры (в градусах Кельвина) от времени для нагревательного элемента некоторого прибора была получена экспериментально и на исследуемом интервале температур определяется выражением закону T(t) = T₀+bt+at², где

t – время в минутах, T₀ = 1400К, а = –10 К/мин², b = 200 К/мин

Известно, что при температуре нагревателя свыше 1760К прибор может испортиться, поэтому его нужно отключать. Определите, через какое наибольшее время после начала работы нужно отключать прибор. Ответ выразите в минутах.

Из условия понятно, что максимально возможная некритическая температура 1760К (при дальнейшем росте прибор может испортиться). Решение задачи сводится к решению неравенства:

Решением являются два интервала: (–∞;2] и [18;+∞).
Так как время величина неотрицательная (t≥0), то для поставленного условия

t ∊[0;2] и [18;+∞).

Получили два интервала удовлетворяющих решению неравенства. Нужно найти, через какое наибольшее время после начала работы необходимо отключать прибор.

Представим физическую картину процесса. Включаем прибор в момент времени t = 0, через 2 минуты температура достигает 1760К. Затем температура повышается, из-за чего прибор может испортиться. Понятно, что отключать его нужно при t = 2 минуты.
Можно проверить, что будет происходить, если прибор не отключить.

Пусть прибор проработает 2,1 минуты, вычислим температуру:

Температура выше допустимой.
Решения при t ≥ 18 не имеют физического смысла для данной задачи.

Второй способ решения.
Начиная с нуля подставляем значения времени в формулу:

Ответ: 2

Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.

Источник