Динамическое моделирование бизнес процессов в транспортных системах

Моделирование бизнес-процесса организации перевозок транспортно-логистической компанией

Моделирование
бизнес-процесса организации перевозок транспортно-логистической компанией

Введение

В основе объектно-ориентированной методологии (ООМ) лежит объектный
подход, когда прикладная предметная область представляется в виде совокупности
объектов, которые взаимодействуют между собой посредством передачи сообщений.

Объектно-ориентированная методология (ООМ) создания автоматизированных
систем состоит из следующих частей:

· объектно-ориентированный анализ (OOA),

· объектно-ориентированное проектирование (OOD),

· объектно-ориентированное программирование (OOР).

ООА — методология анализа сущностей реального мира на основе понятий
класса и объекта, составляющих словарь предметной области, для понимания и
объяснения того, как они (сущности) взаимодействуют между собой.

ООD — методология проектирования, соединяющая в себе процесс объектной
декомпозиции, опирающийся на выделение классов и объектов, и приемы
представления моделей, отражающих логическую (структура классов и объектов) и
физическую (архитектура моделей и процессов) структуру системы.Р -совокупность
идей и понятий, определяющая стиль написания программ, в которой основными
концепциями являются понятия объектов и классов.

При проектировании сложной или достаточно объёмной системы её, как
правило, делят на части, каждую из которых затем рассматривают и разрабатывают
отдельно. Два основных подхода к декомпозиции систем:
функционально-ориентированный, основанный на функциональной декомпозиции, при
которой структура системы описывается в терминах иерархии ее функций и структур
данных; и объектно-ориентированный, при котором структура системы описывается в
терминах объектов и связей между ними, а поведение системы описывается в
терминах обмена сообщениями между объектами.

Объектно-ориентированное проектирование — это методология проектирования,
соединяющая в себе процесс объектной декомпозиции и приемы представления
логической и физической, а также статической и динамической моделей
проектируемой системы.

Основные понятия объектно-ориентированного проектирования: объект, класс,
атрибут, операция, полиморфизм, наследование, компонент, связь.

Объект — это сущность предметной области, имеющая четко определяемое
поведение. Любой объект обладает состоянием, поведением и индивидуальностью.
Состояние объекта определяется значениями его свойств (атрибутов) и связями с
другими объектами, оно может меняться со временем. Поведение определяет
действия объекта и его реакцию на запросы от других объектов. Поведение
представляется с помощью набора сообщений, воспринимаемых объектом (операций,
которые может выполнять объект). Индивидуальность — это свойства объекта,
отличающие его от всех других объектов.

Структура и поведение схожих объектов определяют общий для них класс.
Класс — это множество объектов, связанных общностью свойств, поведения, связей
и семантики. Любой объект является экземпляром класса. Определение классов и
объектов — одна из самых сложных задач объектно-ориентированного
проектирования.

Атрибут — поименованное свойство класса, определяющее диапазон допустимых
значений, которые могут принимать экземпляры данного свойства. Атрибуты могут
быть скрыты от других классов, это определяет видимость атрибута: рublic
(общий, открытый); private (закрытый, секретный); protected (защищенный).

Определенное воздействие одного объекта на другой с целью вызвать
соответствующую реакцию называется операцией или посылкой сообщения. Операция —
это реализация услуги, которую можно запросить у любого объекта данного класса.
Операции реализуют связанное с классом поведение, его обязанности. Описание
операции включает четыре части: имя; список параметров; тип возвращаемого
значения; видимость.

Наследование — это построение новых классов на основе существующих с
возможностью добавления или переопределения свойств (атрибутов) и поведения
(операций).

Компонент — это относительно независимая и замещаемая часть системы,
выполняющая четко определенную функцию в контексте заданной архитектуры. Виды
компонентов: компонент исходного кода; компонент времени выполнения; исполняемый
компонент.

Между элементами объектной модели существуют различные виды связей:

· ассоциация — это семантическая связь между классами;

· агрегация — более сильный тип связи между целым и его
частями;

· зависимость — связь между двумя элементами модели, при
которой изменения в спецификации одного элемента могут повлечь за собой
изменения в другом элементе;

· обобщение — связь «тип — подтип».

Метод объектно-ориентированного проектирования основывается на:

· модели построения системы как совокупности объектов
абстрактного типа данных;

· модульной структуре программ;

· нисходящем проектировании, используемом при выделении
объектов.

В объектно-ориентированном проектировании выделяют следующие
фундаментальные понятия:

Инкапсуляция.

Концепция сокрытия в как бы «капсуле» всей информации об
объекте, то есть объединение в некое целое данных и процедур (методов) их
обработки. Единицей инкапсуляции в OOD является объект, в котором содержатся и
данные состояния объекта и сообщения, которые объект может обрабатывать. Т.е.
Инкапсуляция означает сочетание структур данных с методами их обработки в
абстрактных типах данных — классах объектов.

Наследование.

Получение от предшественника — такое соотношение между классами,
находящимися в некоторой определенной иерархии, при которой один класс
моделирует поведение и свойства другого класса, добавляя свою специфику. Класс
поведение которого наследуется называется суперклассом, а класс, который
наследует поведение, называется подклассом.

Полиморфизм.

Возможность единообразного обращения (посылки объектам одноименных
сообщений) при сохранении уникального поведения объектов. Другими словами,
поскольку поведение объектов определяется методами, метод, ассоциированный с
одним и тем же именем сообщения, допускает различные реализации для разных
классов. Полиморфизм — способность объекта реагировать на запрос (вызов метода)
сообразно своему типу, при этом одно и то же имя метода может использоваться
для различных классов объектов.

Для различных методик объектно-ориентированного проектирования характерны
следующие черты:

· объект описывается как модель некоторой сущности реального
мира;

· объекты, для которых определены места хранения,
рассматриваются во взаимосвязи, и применительно к ним создаются программные
модули системы.

Выделено четыре этапа объектно-ориентированного проектирования:

· разработка диаграммы аппаратных средств системы обработки
данных, показывающей процессоры, внешние устройства, вычислительные сети и их
соединения;

· разработка структуры классов, описывающей связь между
классами и объектами;

· разработка диаграмм объектов, показывающих взаимосвязи с
другими объектами;

· разработка внутренней структуры программного продукта.

История развития языка UML берет начало с октября 1994 года, когда Гради
Буч и Джеймс Румбах из Rational Software Corporation начали работу по
унификации методов Booch и ОМТ. Хотя сами по себе эти методы были достаточно
популярны, совместная работа была направлена на изучение всех известных
объектно-ориентированных методов с целью объединения их достоинств. При этом Г.
Буч и Дж. Румбах сосредоточили усилия на полной унификации результатов своей
работы. Проект так называемого унифицированного метода (Unified Method) версии
0.8 был подготовлен и опубликован в октябре 1995 года. Осенью того же года к ним
присоединился А. Джекобсон, главный технолог из компании Objectory AB (Швеция),
с целью интеграции своего метода OOSE с двумя предыдущими.

Вначале авторы методов Booch, ОМТ и OOSE предполагали разработать
унифицированный язык моделирования только для этих трех методик. С одной
стороны, каждый из этих методов был проверен на практике и показал свою
конструктивность при решении отдельных задач ООАП. Это давало основание для
дальнейшей их модификации на основе устранения имеющегося несоответствия
отдельных понятий и обозначений. С другой стороны, унификация семантики и
нотации должна была обеспечить некоторую стабильность на рынке
объектно-ориентированных CASE-средств, которая необходима для успешного
продвижения соответствующих программных инструментариев. Наконец, совместная
работа давала надежду на существенное улучшение всех трех методов.

Начиная работу по унификации своих методов, Г. Буч, Дж. Румбах и А.
Джекобсон сформулировали следующие требования к языку моделирования. Он должен:

· Позволять моделировать не только программное обеспечение, но
и более широкие классы систем и бизнес-приложений, с использованием
объектно-ориентированных понятий.

· Явным образом обеспечивать взаимосвязь между базовыми
понятиями для моделей концептуального и физического уровней.

· Обеспечивать масштабируемость моделей, что является важной
особенностью сложных многоцелевых систем.

· Быть понятен аналитикам и программистам, а также должен
поддерживаться специальными инструментальными средствами, реализованными на
различных компьютерных платформах.

Разработка системы обозначений или нотации для ООАП оказалась непохожей
на разработку нового языка программирования. Во-первых, необходимо было решить
две проблемы:

. Должна ли данная нотация включать в себя спецификацию требований?

. Следует ли расширять данную нотацию до уровня языка визуального
программирования?

Во-вторых, было необходимо найти удачный баланс между выразительностью и
простотой языка. С одной стороны, слишком простая нотация ограничивает круг
потенциальных проблем, которые могут быть решены с помощью соответствующей
системы обозначений. С другой стороны, слишком сложная нотация создает
дополнительные трудности для ее изучения и применения аналитиками и
программистами. В случае унификации существующих методов необходимо учитывать
интересы специалистов, которые уже имеют опыт работы с ними, поскольку внесение
серьезных изменений в новую нотацию может повлечь за собой непонимание и
неприятие ее пользователями прежних методик. Чтобы исключить неявное
сопротивление со стороны отдельных специалистов, необходимо учитывать интересы
самого широкого круга пользователей. Последующая работа над языком UML должна
была учесть все эти обстоятельства.

Усилия Г. Буча, Дж. Румбаха и А. Джекобсона привели к появлению первых
документов, содержащих описание собственно языка UML, эти документы послужили
своеобразным катализатором для широкого обсуждения языка UML различными
категориями специалистов. Первые отзывы и реакция на язык UML указывали на
необходимость его дополнения отдельными понятиями и конструкциями.

В это же время стало ясно, что некоторые компании и организации видят в
языке UML линию стратегических интересов для своего бизнеса. Компания Rational
Software вместе с несколькими организациями, изъявившими желание выделить ресурсы
для разработки строгого определения версии 1.0 языка UML, учредила консорциум
партнеров UML, в который первоначально вошли такие компании, как Digital
Equipment Corp., HP, i-Logix, Intellicorp, IBM, ICON Computing, MCI
Systemhouse, Microsoft, Oracle, Rational Software, TI и Unisys. Эти компании
обеспечили поддержку последующей работы по более точному и строгому определению
нотации, что привело к появлению версии 1.0 языка UML. В январе 1997 года был
опубликован документ с описанием языка UML 1.0, как начальный вариант ответа на
запрос предложений RTP. Эта версия языка моделирования была достаточно хорошо
определена, обеспечивала требуемую выразительность и мощность и предполагала
решение широкого класса задач.

Специфика языка UML заключается в том, что он определяет семантическую
метамодель, а не модель конкретного интерфейса и способы представления или
реализации компонентов.

Из более чем 800 компаний и организаций, входящих в настоящее время в
состав консорциума OMG, особую роль продолжает играть Rational Software
Corporation, которая стояла у истоков разработки языка UML. Эта компания
разработала и выпустила в продажу одно из первых инструментальных CASE-средств
Rational Rose 98, в котором был реализован язык UML.

В январе 1997 года целый ряд других компаний, среди которых были IBM,
ObjecTime, Platinum Technology и некоторые другие, представили на рассмотрение
OMG свои собственные ответы на запрос предложений RFP. В дальнейшем эти
компании присоединились к партнерам UML, предлагая включить в язык UML некоторые
свои идеи. В результате совместной работы с партнерами UML была предложена
пересмотренная версия 1.1 языка UML. Основное внимание при разработке языка UML
1.1 было уделено достижению большей ясности семантики языка по сравнению с UML
1.0, а также учету предложений новых партнеров. Эта версия языка была
представлена на рассмотрение OMG и была одобрена и принята в качестве стандарта
OMG в ноябре 1997 года.

В настоящее время все вопросы дальнейшей разработки языка UML
сконцентрированы в рамках консорциума OMG. Соответствующая группа специалистов
обеспечивает публикацию материалов, содержащих описание последующих версий
языка UML и запросов предложений RFP по его стандартизации. Очередной этап
развития данного языка закончился в марте 1999 года, когда консорциумом OMG
было опубликовано описание языка UML 1.3.

Статус языка UML определен как открытый для всех предложений по его
доработке и совершенствованию. Сам язык UML не является чьей-либо
собственностью и не запатентован кем-либо, хотя указанный выше документ защищен
законом об авторском праве. В то же время аббревиатура UML, как и некоторые
другие, является торговой маркой их законных владельцев, о чем следует
упомянуть в данном контексте.

Язык UML ориентирован для применения в качестве языка моделирования
различными пользователями и научными сообществами для решения широкого класса
задач ООАП. Многие специалисты по методологии, организации и поставщики
инструментальных средств обязались использовать язык в своих разработках. При
этом термин «унифицированный» в названии UML не является случайным и
имеет два аспекта. С одной стороны, он фактически устраняет многие из
несущественных различий между известными ранее языками моделирования и
методиками построения диаграмм. С другой стороны, создает предпосылки для
унификации различных моделей и этапов их разработки для широкого класса систем,
не только программного обеспечения, но и бизнес-процессов. Семантика языка UML
определена таким образом, что она не является препятствием для последующих
усовершенствований при появлении новых концепций моделирования.

Унифицированный язык моделирования UML стал основой для целого спектра
различных средств поддержки разработки программного обеспечения — CASE-средств
(Computer-Aided Software Engineering).

Первоначальное значение термина, ограниченное вопросами автоматизации
разработки программного обеспечения (ПО), в настоящее время приобрело новый
смысл, и теперь это понятие охватывает процесс разработки сложных
информационных систем в целом.

Также под термином CASE-средства понимаются программные средства,
поддерживающие процессы создания и сопровождения подобных систем, включая
анализ и формулировку требований, проектирование прикладного ПО (приложений) и
баз данных, генерацию кода, тестирование, документирование, обеспечение
качества, конфигурационное управление и управление проектом и т. д.

К появлению CASE-технологии способствовали и такие факторы, как:

· подготовка аналитиков и программистов, восприимчивых к
концепциям модульного и структурного программирования;

· широкое внедрение и постоянный рост производительности
компьютеров, позволившие использовать эффективные графические средства и
автоматизировать большинство этапов проектирования;

· внедрение сетевой технологии, предоставившей возможность
объединения усилий отдельных исполнителей в единый процесс проектирования путем
использования разделяемой базы данных, содержащей необходимую информацию о
проекте.

Таким образом, CASE-технология представляет собой методологию
проектирования ИС, а также набор инструментальных средств, позволяющих в
наглядной форме моделировать предметную область, анализировать эту модель на
всех этапах разработки и сопровождения ИС и разрабатывать приложения в
соответствии с потребностями пользователей. Большая часть CASE-средств
использует методологию структурного (в основном) или ориентированного анализа и
проектирования, использующих спецификации в виде диаграмм или текстов для
описания внешних требований, связей между моделями системы, динамики поведения
системы и архитектуры программных средств.

Современные CASE-средства охватывают обширную область поддержки
многочисленных технологий проектирования информационных систем — от простых
средств анализа и документирования до полномасштабных средств автоматизации,
покрывающих весь жизненный цикл ПО.

Все современные CASE-средства можно классифицировать по типам и
категориям. Классификация по типам отражает функциональную ориентацию
CASE-средств на те или иные процессы жизненного цикла. Помимо этого
CASE-средства можно классифицировать по категориям, применяемым методологиям и
моделям систем и БД; степени интегрированности с СУБД; доступным платформам.

· широкое разнообразие качества и возможностей CASE-средств;

· относительно небольшое время использования CASE-средств в
различных организациях и недостаток опыта их применения;

· широкое разнообразие в практике внедрения различных
организаций;

· отсутствие детальных метрик и данных для уже выполненных и
текущих проектов;

· широкий диапазон предметных областей проектов;

· различная степень интеграции CASE-средств в различных
проектах.

К недостаткам CASE-средств можно отнести необходимость долгосрочных
затрат на эксплуатацию, частому появлению новых версий и возможному быстрому
моральному старению средств, а также постоянным затратам на обучение и
повышение квалификации персонала.

Но все же грамотное, продуманное и обоснованное использование
CASE-технологии способно принести следующие выгоды:

· высокий уровень технологической поддержки процессов разработки
и сопровождения ПО;

· положительное воздействие на некоторые или все из
перечисленных факторов: производительность, качество продукции, соблюдение
стандартов, документирование;

· приемлемый уровень отдачи от инвестиций в CASE-средства.

Среди всех фирм-производителей CASE-средств именно компания IBM Rational
Software Corp. (до августа 2003 года — Rational Software Corp.) одна из первых
осознала стратегическую перспективность развития объектно-ориентированных
технологий анализа и проектирования программных систем. Эта компания выступила
инициатором унификации языка визуального моделирования в рамках консорциума
OMG, что, в конечном итоге, привело к появлению первых версий языка UML. И эта
же компания первой разработала инструментальное объектно-ориентированное
CASE-средство, в котором был реализован язык UML как базовая нотация
визуального моделирования.Rose — CASE-средство фирмы Rational Software
Corporation (США) — предназначено для автоматизации этапов анализа и
проектирования ПО, а также для генерации кодов на различных языках и выпуска
проектной документации.Rational Rose — популярное средство визуального
моделирования, которое считается стандартом де-факто среди средств визуального
проектирования приложений. Этот продукт входит в состав пакета IBM Rational
Suite и предназначен для моделирования программных систем с использованием
широкого круга инструментальных средств и платформ. Инструментальное средство
IBM Rational Rose расширяет возможности моделирования программных систем,
выходящих за рамки платформы J2EE и инструментальных средств моделирования в
составе IBM Rational Professional Bundle.

Являясь простым и мощным решением для визуальной разработки
информационных систем любого класса, Rational Rose позволяет создавать,
изменять и проверять корректность модели. Rational Rose объединяет команду
разработчиков на базе универсального языка моделирования UML, который
определяет стандартную графическую символику для описания архитектуры ПО. Любые
участники проекта — аналитики, специалисты по моделированию, разработчики и
другие — могут использовать модели, построенные в Rational Rose, для большей
эффективности создания конечного продукта. Rose предлагает плавный процесс
разработки ИС. Любые модели, создаваемые с помощью данного средства, являются взаимосвязанными:
бизнес-модель, функциональная модель, модель анализа, модель проектирования,
модель базы данных, модель компонентов и модель физического развертывания
системы.

Возможности по созданию и использованию шаблонов архитектурных решений
позволяют эффективно использовать опыт, накопленный в предыдущих проектах.Rose
является ведущим инструментом визуального моделирования в программной
индустрии, благодаря полноценной поддержке UML и многоязыковой поддержке
командной разработки. Инструмент полностью поддерживает
компонентно-ориентированный процесс создания ИС.

Достоинства продукта Rational Rose

· мощный графический язык моделирования предметной области,
обладающий высоким уровнем формализации и поддерживающий
объектно-ориентированную методологию;

· удобная навигация между элементами модели при помощи
«инспектора проекта»;

· хранение результатов проектирования в виде единой модели;

· поддержка работы над проектом группы разработчиков;

· данное CASE средство может быть применено для создания
разнообразного объектно-ориентированного программного обеспечения, в первую
очередь для платформы Windows, а так же на языке Java;

· на всех этапах разработки применяется язык UML, и проект
программного средства представляет собой единую модель;

· возможность конфигурирования системы с помощью модулей
расширения;

· в наибольшей степени подходит для разработки крупных
информационных систем, так как реализует большую часть функций ARIS и
ERwin/BPwin. И т.д.

Недостатки продукта Rational Rose

· слабо реализована поддержка проектирования ПО для других
операционных систем, почти все стандартные рабочие среды ориентированны на
построение Windows-приложений, единственным способом написания приложения для
не-Windows операционной системы является использование языка Java, производительность
которого, пока, оставляет желать лучшего.

· сложность самого языка UML также накладывает определенные
ограничения на привлечение к работам над проектами непрофессионалов,

· нельзя показать и удалить неиспользуемые объекты в отличие от
BPWin;

· недостаточно функциональная графика (нельзя менять толщину
линий, надписи не центрируются, текст не всегда можно поместить целиком, иногда
он обрезается);

· не поддерживает функционально-стоимостной анализ;

· нет возможности отобразить потоки данных между объектами или
процессами.

В результате разработки проекта с помощью CASE-средства Rational Rose
формируются следующие документы:

· диаграммы классов;

· диаграммы состояний;

· диаграммы сценариев;

· диаграммы модулей;

· диаграммы процессов;

· спецификации классов, объектов, атрибутов и операций

· заготовки текстов программ;

· модель разрабатываемой программной системы.

Последний из перечисленных документов является текстовым файлом,
содержащим всю необходимую информацию о проекте (в том числе необходимую для
получения всех диаграмм и спецификаций).

Тексты программ являются заготовками для последующей работы
программистов. Состав информации, включаемой в программные файлы, определяется
либо по умолчанию, либо по усмотрению пользователя. В дальнейшем эти исходные
тексты развиваются программистами в полноценные программы.

1.
Описание предметной области

В данном курсовом проекте описан бизнес-процесс организации перевозок
транспортно-логистической компанией. На сегодняшний день рынок насыщен
транспортно-логистическими компаниями. Как правило, такие компании не имеют
собственного транспортного парка, поэтому они сотрудничают с компаниями
перевозчиками, которые непосредственно и осуществляют перевозку. Таким образом,
транспортно-логистическая компания выступает связующим звеном между
грузоотправителем и перевозчиком. Основными задачами транспортно-логистической
компании являются:

1. разработка оптимальной транспортно-технологической схемы
перевозки;

. организация перевозки.

Разработкой транспортно-технологической схемы перевозки занимается
логистический отдел. Этот процесс включает в себя:

· выбор вида и типа транспортного средства;

· выбор вида транспортировки;

· выбор маршрута.

В организации перевозки задействован не один отдел, здесь принимает
участие и директор, и менеджер, и бухгалтер, а также экспедиторы. Данный этап
включает в себя:

· прием и обработку заявок на перевозку;

· заключение договоров с клиентами;

· проведение необходимых бухгалтерских операций;

· экспедирование перевозки;

· таможенное оформление.

В данном курсовом проекте рассматривается этап организации перевозок.

2.
Моделирование проектируемой системы

.1
Диаграмма вариантов использования

Диаграмма вариантов использования (use case diagram) — диаграмма, на
которой изображаются отношения между актерами и вариантами использования.

Назначение данной диаграммы состоит в следующем: проектируемые
бизнес-процессы представляется в форме так называемых вариантов использования,
с которыми взаимодействуют внешние сущности или актеры. При этом актером
называется любой объект, субъект или система, взаимодействующая с моделируемой
компанией извне. Это может быть человек, техническое устройство, программа или
система, которая служит источником воздействия на моделируемые бизнес процессы
систему так, как определит разработчик. Вариант использования служит для
описания сервисов и функций, которые компания предоставляет заказчику. Другими
словами каждый вариант использования определяет набор действий, совершаемый
компаний при работе с заказчиком — актером. При этом ничего не говорится о том,
каким образом будет реализовано взаимодействие актеров с компанией и собственно
выполнение вариантов использования.

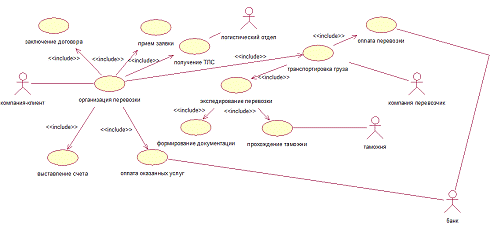
На рисунке 1 представлена диаграмма вариантов использования
бизнес-процесса организации перевозок. На диаграмме присутствуют 5 действующих
лиц (актеров): логистический отдел, компания клиент, компания перевозчик,
таможня и банк. Они являются внешними по отношению к моделируемому
бизнес-процессу компании, сущностями которые взаимодействуют с компанией.

Компания клиент (грузоотправитель) обращается в транспортно-логистическую
компанию с целью получения услуги по организации и осуществлению перевозки. В
свою очередь наша система обращается в логистический отдел, что бы получить
ТЛС, а так же обращается к компании-перевозчику для осуществления
транспортировки груза. Так как наша компания занимается организацией и
осуществлением международных перевозок, система так же взаимодействует с
таможней. Для проведения денежных расчетов система взаимодействует с банком.

Выделен 1 основной вариант использования — «организация перевозки». После
обращения компании-клиента в нашу фирму начинается процесс организации
перевозки. Сначала заключается договор на перевозку, а также оформляется заявка
на перевозку. После чего получается ТЛС. Для начала транспортировки груза
необходимо произвести расчет за перевозку с компанией-перевозчиком, затем
происходит транспортировка груза с экспедиционными услугами, которые
подразумевают под собой прохождение таможни и сбор всех необходимых документов
на пути следования. По окончании перевозки необходимо выставить счет клиенту и
принять оплату.

Варианты использования определяют функциональные возможности. Каждый из
них представляет определенный способ использования. Таким образом, каждый
вариант использования соответствует последовательности действий для того, чтобы
клиент мог получить определенный результат.

автоматизированный объектный ориентированный логистический

Рисунок 1 — Диаграмма вариантов использования

2.2
Диаграмма классов

Диаграмма классов является центральным звеном методологии
объектно-ориентированных анализа и проектирования. Диаграмма классов показывает
классы и их отношения, тем самым, представляя логический аспект проекта. На
стадии анализа диаграммы классов используются, чтобы выделить общие роли и
обязанности сущностей, обеспечивающих требуемое поведение проектируемого
бизнес-процесса. На стадии проектирования используются, чтобы передать
структуру классов, формирующих архитектуру проектируемой области.

Диаграмма классов предназначена для представления статической структуры
модели проектируемых бизнес-процессов. При этом диаграмма классов может
содержать интерфейсы, пакеты, отношения и даже отдельные экземпляры
классификаторов, такие как объекты и связи. Когда говорят о данной диаграмме,
имеют в виду статическую структурную модель проектируемой области, т. е.
графическое представление таких структурных взаимосвязей логической модели
проектируемой области, которые не зависят от времени.

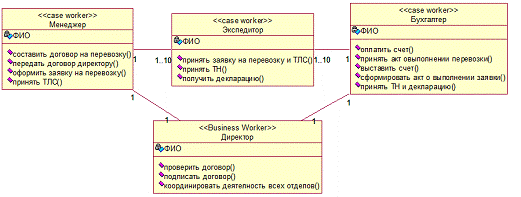
На рисунке 2 представлена диаграмма классов.

Данная диаграмма показывает взаимосвязи между сущностями бизнес-процесса,
описывает внутреннюю структуру и типы отношений.

Рисунок 2 — Диаграмма классов

2.3
Диаграмма последовательности

Является моделью, описывающей поведение взаимодействующих групп объектов.
Охватывает поведение только одного варианта использования.

На диаграммах последовательности могут быть представлены особенности
взаимодействия элементов моделируемых бизнес-процессов. На диаграмме последовательности
неявно присутствует ось времени, что позволяет визуализировать временные
отношения между передаваемыми сообщениями. С помощью диаграммы
последовательности можно представить взаимодействие элементов модели как
своеобразный временной график «жизни» всей совокупности объектов,
связанных между собой для реализации варианта достижения цели или выполнения
какой-либо задачи.

На рисунке 3 представлена диаграмма последовательности действий
организации перевозки. При обращении компании-клиента в транспортно-логистическую
компанию заключается договор на перевозку, в следствии взаимодействия
компании-клиента, менеджера и директора. Затем оформляется заявка на перевозку
путем взаимодействия компании-клиента с менеджером. После чего менеджер,
взаимодействуя с логистическим отделом получает ТЛС и передает ее и заявку
экспедитору. Затем происходит ряд операций по расчету с компанией-перевозчиком,
в котором участвуют менеджер, бухгалтер и сама компания-перевозчик. После чего
происходит осуществление перевозки с прохождением таможни при взаимодействии
экспедитора, таможни и компании-перевозчика. После того как перевозка завершена
происходит расчет с компанией-клиентом.

2.4 Диаграмма кооперации

Разновидность диаграммы взаимодействия, которая выделяет структурную организацию
объектов, посылающих и принимающих сообщения. Диаграммы последовательности и
кооперации изоморфны.

Диаграмма кооперации предназначена для описания поведения проектируемого
бизнес-процесса на уровне отдельных объектов, которые обмениваются между собой
сообщениями, чтобы достичь нужной цели или реализовать некоторый вариант
использования.

На диаграмме кооперации размещаются объекты, представляющие собой
экземпляры классов, связи между ними, которые в свою очередь являются
экземплярами ассоциаций и сообщения. Связи дополняются стрелками сообщений, при
этом показываются только те объекты, которые участвуют в реализации
моделируемой кооперации. Далее, как и на диаграмме классов, показываются
структурные отношения между объектами в виде различных соединительных линий.
Связи могут дополняться именами ролей, которые играют объекты в данной
взаимосвязи. И изображаются динамические взаимосвязи — потоки сообщений в форме
стрелок с указанием направления рядом с соединительными линиями между
объектами, при этом задаются имена сообщений и их порядковые номера в общей
последовательности сообщений.

На рисунке 4 представлена диаграмма кооперации, которая формируется из
диаграммы последовательности.

2.5
Диаграмма состояний

Диаграммы состояний используются для моделирования динамических аспектов
моделируемого бизнес-процесса. По большей части под этим подразумевается
моделирование поведения реактивных объектов. Реактивным называется объект,
поведение которого лучше всего характеризуется его реакцией на события, произошедшие
вне его собственного контекста.

Каждый объект моделируемой области, обладающий определенным поведением,
может находится в определенных состояниях, переходить из состояния в состояние,
совершая определенные действия в процессе реализации сценария поведения
объекта. Поведение большинства объектов реальных систем можно представить с
точки зрения теории конечных автоматов, то есть поведение объекта отражается в
его состояниях, и данный тип диаграмм позволяет отразить это графически.

Главное предназначение этой диаграммы — описать возможные
последовательности состояний и переходов, которые в совокупности характеризуют
поведение элемента модели в течение его жизненного цикла.

На рисунке 5 представлена диаграмма состояний, которая отображает
деятельность бухгалтера, заключающуюся в получение счета от
компании-перевозчика и его оплате, а также в получение документов
подтверждающих завершение перевозки — акта, декларации и ТН, на основании
которых бухгалтер выставляет счет компании-клиенту, формирует акт об оказанных
услугах и передает все необходимые документы компании-клиенту.

2.6 Диаграмма деятельности

Они позволяют детализировать особенности алгоритмической и логической
реализации выполняемых компаний операций.

Основным направлением использования диаграмм деятельности является
визуализация особенностей реализации операций классов, когда необходимо
представить алгоритмы их выполнения. При этом каждое действие может являться
выполнением операции некоторого класса либо ее части, позволяя использовать
диаграммы деятельности для описания реакций на внутренние события компании.

Диаграммы деятельности — частный случай диаграмм состояний. Они позволяют
реализовать в языке UML особенности процедурного и синхронного управления,
обусловленного завершением внутренних действий и деятельности. В контексте
языка UML деятельность представляет собой совокупность отдельных вычислений,
выполняемых автоматом. При этом отдельные элементарные вычисления могут
приводить к результату или действию. На диаграмме деятельности отображается
логика или последовательность перехода от одной деятельности к другой, при этом
внимание фиксируется на результате деятельности. Диаграмма деятельности
предназначена для моделирования поведения любого объекта, под объектом может
выступать как сотрудник компании так и внешний актер, хотя время в явном виде
отсутствует на этой диаграмме.

На рис. 6 представлена диаграмма деятельности менеджера. Менеджер
составляет договор на перевозку, а затем отдает его на проверку директору.
После чего договор либо подлежит исправлению и правится менеждером, либо
подлежит подписанию и в этом случае менеджер подписывает договор с клиентом,
затем отдает договор директору для подписания. После этого происходит
оформление заявки на перевозку, а так же дается указание логистическому отделу
на разработку ТЛС. После происходит получение ТЛС и передача ее и заявки
экспедитору.

Заключение

При моделировании бизнес-процесса организации перевозок
транспортно-логистической компанией использовался объектно-ориентированный
подход, с использованием объектно-ориентированного case средства Rational Rose, которое позволило наглядным
образом представить область моделирования в виде графической модели
(совокупности диаграмм), благодаря мощному графическому языку моделирования
предметной области, обладающему высоким уровнем формализации.

При моделировании бизнес-процесса организации перевозок
транспортно-логистической компанией были раскрыты основные функции данного
процесса.

Список
литературы

1. Конспект лекций ПИС.

2. Электронный самоучитель Rational Rose 98/2000, Леоненков.

Источник

Анна Сергеевна Дьяченко

Эксперт по предмету «Логистика»

Задать вопрос автору статьи

Определение 1

Моделирование транспортных процессов — это замещение реальных транспортных процессов другим объектом (моделью) с целью получения через исследование этого объекта информации о важнейших свойствах реальных транспортных процессов.

Общее представление о моделировании транспортных процессов

Проблема управления транспортными потоками очень актуальна в настоящее время. Особенно это касается больших городов, где значительными темпами увеличивается количество личного и общественного транспорта. Результатом этого является перегруженность городских дорог, возникновение многочасовых пробок, увеличение количества аварийных ситуаций, затруднение движения пешеходов и др. Для того чтобы решить указанные проблемы в принципе или минимизировать их негативные эффекты лично для себя, в логистике практикуется создание моделей / моделирование реальных транспортных процессов.

Сделаем домашку
с вашим ребенком за 380 ₽

Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online

Вообще моделированием называют процесс создания моделей. Модели, в свою очередь, представляют собой объекты, на которые переносятся значимые признаки реальных объектов (оригиналов). После чего по отношению к моделям начинают применять те методы исследования, которые в силу ряда причин не могли быть применимы в отношении объектов-оригиналов. Благодаря этому исследователи получают полезную, необходимую для них информацию о реальном объекте, которая может быть использована при решении практических проблем.

Важной чертой любой модели является ее адекватность. Речь идет про свойство модели быть основой для прогнозирования событий (в нашем случае — тех событий, которые имеют место в транспортных системах и процессах) и дачи подтверждаемых результатов. Только при работе с адекватной моделью можно получить практически значимые результаты и принять эффективные управленческие решения.

Математическое моделирование транспортных процессов

При исследовании транспортных процессов и систем чаще всего используются методы математического моделирования. Оно является разделом мысленного моделирования и заключается в установлении соответствия между данным реальным транспортным процессом и некоторого математического объекта (модели).

«Моделирование транспортных процессов» 👇

Любая математическая модель описывает реальные транспортные процессы лишь с некоторой степенью приближения к реальности. Строгие методы решений обычно не используются. Широкое распространение получили смекалка и интуиция инженерно-технического и управленческого персонала, а также внесение упрощающих допущений.

Методы решений транспортных задач, когда точно определить границы их применения и дать оценку допустимым погрешностям нельзя, называются эвристическими. Эти методы объединяются в таком разделе математики, как математическое программирование.

При решении задач качественной организации и адаптации транспортных процессов широко используются следующие методы математического программирования:

Корреляционно-регрессионный анализ;
Линейное программирование;
Динамическое программирование;
Целочисленное программирование;
Теория массового обслуживания;
Метод сетевого планирования и управления;
Дисперсионный анализ;
Корреляционно-спектральный анализ;
Кибернетический метод;
Символическая (математическая) логика.

Математическое моделирование, которое применяется в процессе решения транспортных задач, обычно подразделяют на два направления — оптимизационное (аналитическое) и имитационное:

Оптимизационное (аналитическое) моделирование транспортных процессов — течение транспортных процессов записывается в виде некоторых функциональных соотношений (например, алгебраических, интегрально-дифференциальных, конечноразностных и т.п.) или логических условий; применяется в отношении систем малой и средней сложности;
Имитационное моделирование транспортных процессов — транспортные процессы описываются путем применения экспертных и кибернетических методов, опытных данных; применяется в отношении систем большой сложности.

Последние годы все активнее стали внедряться технологии имитационного моделирования транспортных процессов. Подспорьем для этого послужило массовое распространение компьютерных технологий, специального программного обеспечения, их высокая производительность и качество работы.

Особенности моделирования транспортных процессов

Моделирование транспортных процессов и систем осуществляется, в первую очередь, для того, чтобы проанализировать эффективность изменения тех или иных транспортно-эксплуатационных показателей. Решение задач, связанных моделированием и анализом реальных транспортных процессов, позволяет соответствующим образом организовать дорожное движение с использованием информационных и информационно-управляющих процессов.

В транспортной сфере методы моделирования достаточно широко используются. В частности, с их помощью решаются следующие задачи:

Составление схем грузопотоков, оптимальных с точки зрения минимизации расстояний перевозки грузов;
Распределение клиентуры между транспортными предприятиями;
Распределение маршрутов между транспортными предприятиями;
Снижение нулевых пробегов транспортных средств;
Маршрутизация (составление маршрутов) перевозок грузов, нацеленная на минимизацию непроизводительных пробегов транспортных средств;
Минимизация времени доставки грузов клиентам;
Определение кратчайших путей между пунктами отправления и назначения и др.

Таким образом, ввиду высокой значимости и присутствия так или иначе во всех сферах общественной жизни транспортные процессы являются одними из самых востребованных на сегодня объектов исследования. Моделирование является популярным методом исследования, который позволяет получить много новой информации об изучаемых транспортных процессах.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

АННОТАЦИЯ

При изучении
данной дисциплины ДС.02 «Моделирование
транспортных процессов и систем»
выполняется курсовой проект.
«Формирование системы оптимальных
грузопотоков», который является
завершающим этапом изучения дисциплины.
Целью курсового проекта являются
закрепление, систематизация и углубление
полученных знаний; приобретение
навыков системного проектирования
прогрессивных перевозочных технологий;
умение пользоваться нормативно-справочной
литературой.

СОДЕРЖАНИЕ

ВВЕДЕНИЕ 2

Задание 2

1.Роль
математических методов в принятии
эффективных управленческих решений
при автомобильных перевозках Виды
моделей и эвристические методы решения
задач 2

2.Понятие
корреляционно-регрессионный анализ 2

3.
Модели линейного программирования
в решении задач автомобильных перевозок
основные понятия, графоаналитический
и симплексный методы 2

4.
Маршрутизация перевозок помашинными
отправками основные этапы решения
задач 2

6.
Методы планирования перевозок по
сборно — развозочным маршрутам 2

7.
Понятие о теории массового обслуживания
в решении задач автомобильных
перевозок 2

Задача
№ 1 2

ЗАДАЧА
№ 2 2

ВЫВОД 2

БИБЛИОГРАФИЧЕСКИЙ
СПИСОК 2

ВВЕДЕНИЕ

Транспортная
система – это совокупность реальных
объектов и связей между ними, которые
используются на определенной территории
для выполнения перевозок.

Автомобильно-дорожный
комплекс России (АДК) включает в себя:
автотранспортные предприятия и
транспортные средства; автомобильные
дороги и организации, поддерживающие
их в рабочем состоянии; организации,
обеспечивающие ремонт и техническое
обслуживание автотранспортных средств;
организацию и систему контроля
транспортными потоками на дорожной
сети; места стыковки автомобилей с
другими видами транспорта.

АДК России имеет
все признаки большой сложной,
динамической системы, так как включает
наличие большого числа взаимодействующих
подсистем и элементов, имеет иерархический
характер построения (подчиненности),
множественность функций, наличие
управления, взаимодействие с окружающей
средой и воздействие случайных
факторов, большую размерность задач.

По мощности
осваиваемых пассажиро- и грузопотоков
отдельные транспортные подсистемы
АДК принято подразделять на 7 групп
(систем).

1. Микросистемы
(маятниковые маршруты с одним автомобилем
и

обратным холостым
пробегом).

2. Особо малые
системы (кольцевые и маятниковые
маршруты с одним автомобилем) различных
типов с несколькими работающими
транспортными средствами.

3. Малые системы
– кольцевые и маятниковые маршруты
различных типов с несколькими
работающими транспортными средствами.
Сюда относятся небольшие транспортные
фирмы и транспортные отделы фирм
малого бизнеса.

4. Средние системы
– совокупность нескольких малых
систем. Сюда относятся, например,
железобетонные заводы, контейнерные
станции, базы снабжения вместе с
транспортными средствами и получателями
товаров.

5. Большие системы
– сюда относятся автомобильные парки
и грузовые АТП с подвижным составом
и их маршрутами.

6. Особо большие
системы — автотранспортные тресты,
производственные управления и
объединения.

7. Суперсистема
включает множество вышеуказанных
систем, например Департамент
автомобильного транспорта России.

Автомобильные
и транспортные процессы в вышеуказанных
системах включают большое количество
задач по управлению АДК, разработке
технологических схем организации
перевозок, формированию систем
оптимальных грузопотоков, маршрутизации
перевозок, формированию сменно-суточных
планов, выбору кратчайших путей
движения, закреплению потребителей
за поставщиками, транспортные задачи
с запретами и по критерию времени и
так далее.

Задание

1. Роль математических
методов в принятии эффективных
управленческих решений при автомобильных
перевозках. Виды моделей и эвристические
методы решения задач.

2. Понятие
корреляционно-регрессионный анализ.

3. Модели линейного
программирования в решении задач
автомобильных перевозок – основные
понятия, графоаналитический и
симплексный методы.

4. Маршрутизация
перевозок помашинными отправками –
основные этапы решения задач.

5. Методы определения
кратчайших расстояний перевозок.

6. Методы
планирования перевозок по сборно —
развозочным маршрутам.

7. Понятие о теории
массового обслуживания в решении
задач автомо- бильных перевозок.

Задача №1

Имеются i=4
пункта отправления груза А₁,
А₂,
А₃,
А₄
и j=6
пунктов назначения груза В₁,
В₂,
В₃,
В₄,
В₅,
В₆.
Обозначим ресурсы груза в i-м
пункте отправления через а_i, i
=1, 2, 3, 4, а потребность каждого j-го
пункта потребления через b_j,
j
= 1, 2, 3, 4, 6.

Заданы расстояния
между пунктами отправления и пунктами
назначения (табл. 1).

Требуется
составить
такой план x_ij
перевозок грузов, который обеспечит
удовлетворение запросов всех
потребителей груза при минимальной
транспортной работе (минимальной
сумме тонно-километров). Задача
является задачей линейного
программирования, при решении
рекомендуется использовать метод
потенциалов.

Исходные данные
для решения задачи (объемы отправления
а_i
и потребления b_j
груза) выбираются из табл. 2 в соответствии
с шифром студента.

Таблица
1

Расстояния
между пунктами, км

Пункты
отправления

Пункты
назначения

В₁

В₂

В₃

В₄

В₅

В₆

А₁

А₂

А₃

А₄

Таблица 2

Объемы перевозок
груза, т

Объемы
отправления и потребления груза, т

Варианты
(последняя цифра шифра студента)

а₁

а₂

а₃

а₄

b₁

b₂

b₃

b₄

b₅

b₆

Задача №2

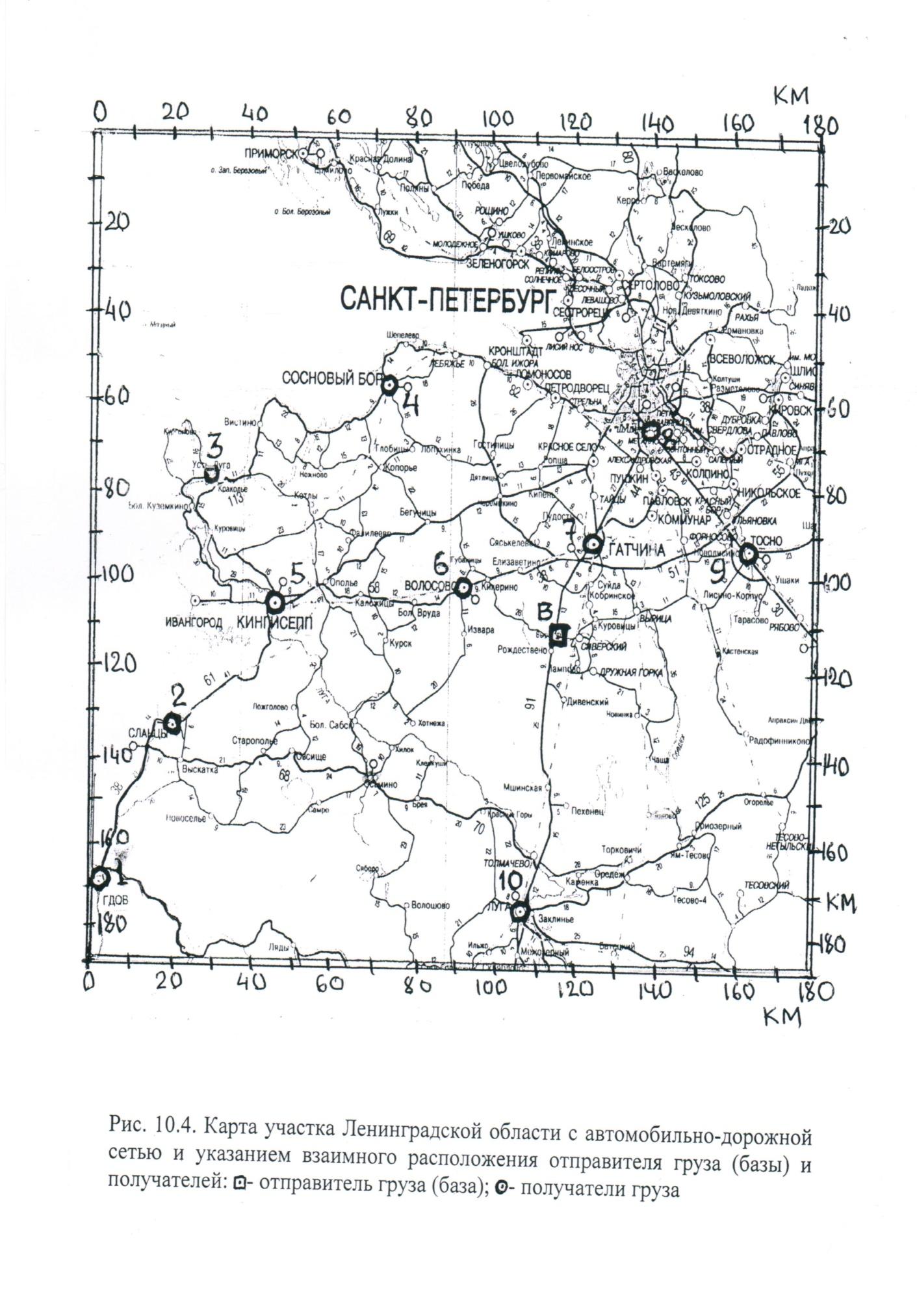
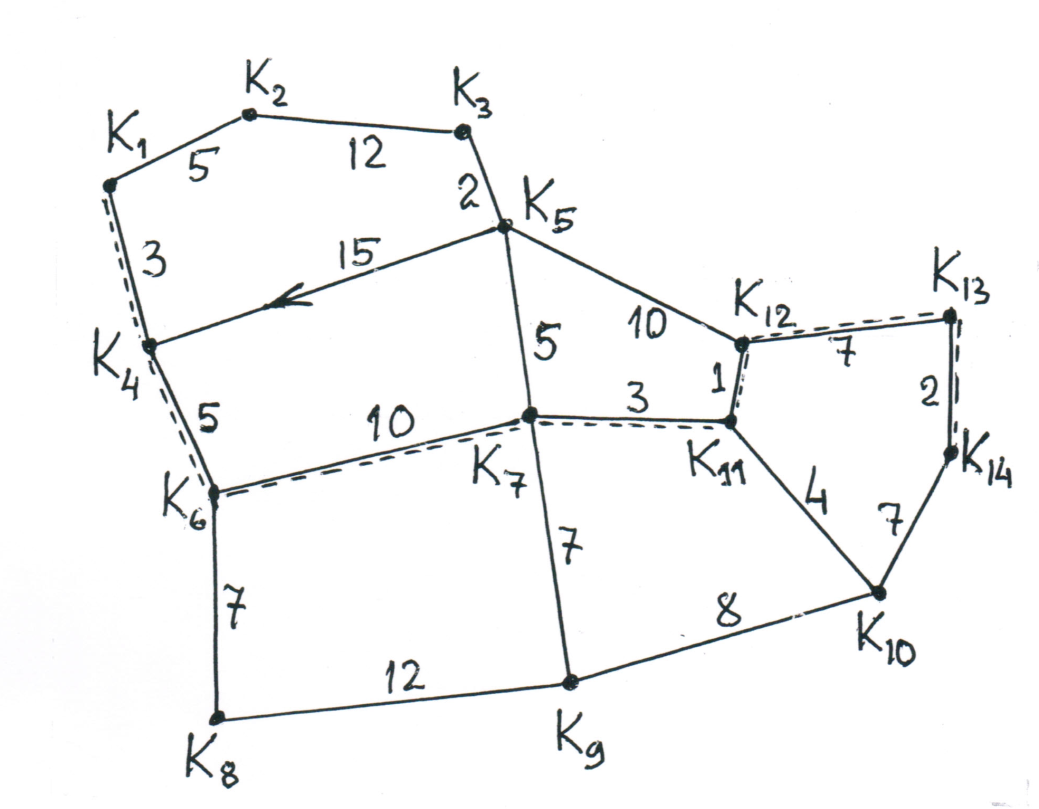
Составить граф
(схему) транспортной сети участка
Ленинградской области, показанного
на рис. 1. Граф представить на чертеже
А1. При составлении графа учесть
основные (главные) дороги, показанные
на рис. 1 толстыми линиями. Вершинами
графа являются отправитель (В) и
получатели (1…10) груза, основные
населенные пункты, перекрестки.
Расстояния между вершинами (длины
звеньев графа) определить по указанному
на рис. 1 масштабу и указать длины на
звеньях графа в км. Участки между
вершинами графа соединять прямыми
линиями (звеньями).

Выполнить
проектирование развозочного маршрута
с пунктом погрузки в точке В и 3 пунктами
разгрузки (рис. 1). Точки разгрузки и
их потребность в грузе выбираются по
предпоследней цифре шифра студента
по табл. 3.

Рис. 1. Карта участка Ленинградской
области с автомобильно-дорожной сетью
и указанием взаимного расположения
отправителя груза (базы) и получателей:
— отправитель груза (база);
— получатель
груза

Критерием выбора
маршрута является минимальное
расстояние перевозок с учетом величин
транспортной работы в т·км.

Таблица 3

Пункты
разгрузки груза и их потребность в
грузе для составления

развозочного
маршрута

Предпоследняя
цифра шифра зачетной книжки студента

Номера пунктов
разгрузки по рис. 1

3,8,10

Потребность
пунктов разгрузки в грузе, m

n3-2т

n8-1т

n10-5т

Роль
математических методов в принятии
эффективных управленческих решений
при автомобильных перевозках Виды
моделей и эвристические методы решения
задач

Значительная
часть внутренних грузовых перевозок
в России выполняется автомобильным
транспортом, и эта часть постоянно
растет. В этом Россия следует за нашим
соседом Евросоюзом, где автомобильные
перевозки составляют уже более 80%
всего внутреннего грузооборота.

Эффективным
способом снижения транспортных затрат
является использование новых технологий
при организации автомобильных
перевозок. К таким новым технологиям
относится математическое моделирование,
позволяющее существенно повышать
качество планирования, маршрутизации
и управления подвижным составом и
снижать себестоимость перевозок на
десятки процентов. Это в первую очередь
относится к перевозкам массовых
грузов (помашинным и мелкопартийным
перевозкам), осуществляемым многими
тысячами отечественных автотранспортных
фирм.

Особо в технологии
математического моделирования следует
отметить бурно развивающийся в
настоящее время раздел «Теория
массового обслуживания». Разрабатываемые
в этом разделе методы позволят
прогнозировать будущее поведение
автотранспортной системы еще на стадии
проектирования, наиболее оптимально
распределять производственные ресурсы
транспортной фирмы, избегать кризисных
явлений, стабильно осуществлять
перевозки грузов по системе
«точно-вовремя». Базой развития этих
методов являются новые спутниковые
технологии позиционирования и
определения в глобальном пространстве
данных по элементам перевозочного
процесса, технологии быстрой передачи
этих данных на центральные компьютеры
транспортных и экспедиторских фирм
и их высокоскоростной обработки с
учетом вероятностных характеристик
транспортных процессов.

Для специалиста,
занимающегося автомобильными
перевозками, владение методами
математического моделирования во
многом определяет уровень его
квалификации и карьерный рост.

Для транспортной
фирмы использование в производстве
технологий математического моделирования
повышает ее конкурентоспособность и
финансовую устойчивость на рынке.

Для городов и
регионов России оптимизация автомобильных
перевозок дает заметный социальный
эффект, так как ведет к снижению
загрязнения атмосферы вредными
выбросами от автомобилей и улучшает
экологическую обстановку в целом.

Для решений
транспортных задач разрабатываются
новые методики, базирующиеся на
использовании новых технологий и
методов расчета.

К таким новым
технологиям относятся моделирование
и использование моделей для решения
задач управления и принятия решений.
Во многих ситуациях они являются
единст

венно возможным
и эффективным методом, позволяющим
получить ответ на поставленный вопрос.

Модель — это
аналог, макет или иной вид отражения
наиболее важных черт, свойств и
результатов транспортных систем и
процессов.

Адекватность
модели — это свойство модели быть
основой для прогнозирования событий,
протекающих в транспортных системах
и процессах, и давать подтверждаемые
результаты.

Моделирование
– это замещение одного объекта другим
с целью получения информации о важнейших
свойствах объекта-оригинала с помощью
объекта-модели.

Теория моделирования
– это теория замещения одних
объектов-оригиналов другими объектами
(моделями) и исследования свойств
объектов на их моделях.

В зависимости
от характера изучаемых процессов в
системе все виды моделирования могут
быть разделены на детерминированные
и стохастические; статические и
динамические; дискретные, непрерывные
и дискретно-непрерывные.

Детерминированное
моделирование отображает детерминированные
процессы, то есть процессы, в которых
предполагается отсутствие всяких
случайных воздействий.

Стохастическое
моделирование отражает вероятностные
процессы и события. В этом случае
анализируется ряд реализаций случайного
процесса и оцениваются средние
характеристики.

Статическое
моделирование
служит для описания поведения объекта
в какой-либо момент времени, а
динамическое
моделирование отражает поведение
объекта во времени.

Дискретное
моделирование служит для описания
процессов, которые предполагаются
дискретными, а непрерывное
отражает непрерывные процессы в
системах.

В зависимости
от формы представления объекта
(системы) можно выделить мысленное и
наглядное моделирование.

При наглядном
моделировании на базе представлений
человека о реальных объектах создаются
различные наглядные модели, отображающие
явления и процессы, протекающие в
объекте (механические, графические и
другие).

При исследовании
транспортных процессов и систем на
автомобильном транспорте наиболее
широко используется математическое
моделирование, являющееся разделом
мысленного
моделирования.

Под математическим
моделированием
понимают установление соответствия
данному реальному транспортному
процессу или системе некоторого
математического объекта, называемого
математической моделью и исследование
этой модели, позволяющее получить
характеристики рассматриваемого
реального транспортного процесса и
транспортной системы.

Любая математическая
модель, как и всякая другая описывает
реальную систему и процесс лишь с
некоторой степенью приближения к
действительности.

При решении
практических задач автомобильно-дорожного
комплекса, как правило, не применяются
строгие методы решений. Широко
используются смекалка и интуиция
инженерно-технического и управленческого
персонала.

В модели реальных
транспортных процессов и систем
вносятся упрощающие допущения. Такой
метод позволяет подобрать для решаемой
задачи из набора средств современной
математики приемлемый алгоритм и
найти хотя бы приближенное решение.

Такие методы
решений задач в условиях, когда нельзя
точно определить границы их применения
и оценить допустимые погрешности,
называются эвристическими.

Преимущества
математического моделирования перед
другими видами (графическим, аналоговым,
механическим и т.д.) заключаются в
широком использовании математических
моделей, низкой стоимости их создания,
быстром получении результатов
исследований, возможности проведения
расчетных экспериментов и проверки
правильности построения модели.

Конечно,
математическая модель всегда является
упрощенной, однако она является
достаточно наглядной и позволяет
адекватно описать транспортную систему
и транспортный процесс.

Математическое
моделирование при решении задач АДК
можно разделить на оптимизационное
(аналитическое) и имитационное.
Соответственно математические модели
можно разделить на аналитические и
имитационные.

Понятие
корреляционно-регрессионный анализ

Корреляция в
переводе с латинского обозначает
соответствие или взаимосвязь.
Корреляционная зависимость отражает
связь между величинами, когда
определенным значениям факториальных
величин соответствует много значений
зависимой величины.

Корреляционный
анализ в задачах моделирования
транспортных процессов и систем имеет
фундаментальное значение, так как
теснота корреляционной связи определяет
структуру модели. Высокая и полная
корреляционная связь требует объединения
величин. Отсутствие или слабость
корреляционных связей позволяют
рассматривать величину как независимую.

Во многих случаях
выбор независимых величин на базе
исследования их корреляционных связей
требует дополнительного экспертного
исследования и решения.

Корреляционная
связь между двумя переменными изучается
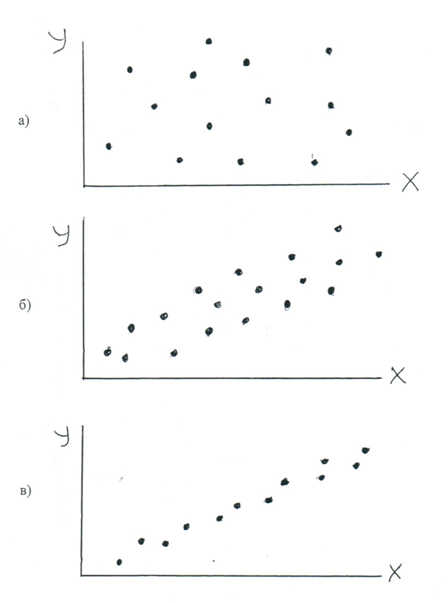
с помощью парной корреляции. О тесноте
корреляционной связи можно судить по
характеру расположения точек на
графике, связующем переменные х
и у.
Такой график называется полем корреляции
(рис. 2). Разброс точек по всему полю
свидетельствует об отсутствии
корреляции (рис. 2,а), рис. 2,б свидетельствует
о слабой умеренной корреляции, рис.
2,в — о полной корреляции.

Рис. 2. Расположение
точек на корреляционном поле:

а) корреляционная
связь отсутствует;

б) слабая и умеренная
корреляционная связь;

в) полная корреляционная
связь

Численное значение
корреляционной связи оценивается
коэффициентом
корреляции r.

Задачей
регрессионного анализа является
установление вида зависимости (1.2)
(зависимости параметра оптимизации
у
от факториальных величин х₁,
х₂…х_n₎.
Указанная зависимость называется
уравнением
регрессии.
Корреляционно-регрессионный анализ
позволяет прогнозировать развитие
рассматриваемого явления и решать
задачу построения модели и ее
оптимизации. Регрессионный анализ
введен в практику расчетов английским
математиком и механиком У.Р. Гамильтоном
в 1840-х годах.

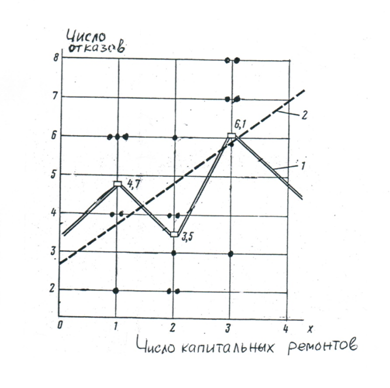
При проведении
регрессионного анализа применяются
понятия парных и множественных
коэффициентов регрессии. На рис. 2
показано корреляционное поле парной
линейной зависимости, отказов
автомобилей в эксплуатации от числа
капитальных ремонтов. Рассмотрение
расположения точек на поле рис. 2
позволяет говорить о слабой корреляционной
зависимости, разброс точек на рис. 2
примерно соответствует рис. 1,б. Из
рис. 3 видно, что если для каждой величины
х
найти средние значения у
и соединить эти точки, то получится
ломанная линия, называемая опытной
линией
регрессии.

Рис. 3. Регрессионная зависимость числа
отказов автомобилей в эксплуатации
от числа капитальных ремонтов:
1-опытная; 2-теоритическая; •-точки
опытных данных; □-средние арифметические
числа отказов автомобилей по каждой
группе

При парной
зависимости опытная линия регрессии
может быть аппроксимирована с помощью
следующих функций:

у = а + b х
– прямая линия;

у = а х²
+ b х + с –
парабола второго порядка;

у =

–
гипербола;

у = а + b lg
х –
логарифмическая функция.

Используются
также показательная и степенная
функции, арифметическая и геометрическая
прогрессии, алгебраический полином,
тригонометрический ряд (ряд Фурье) и
другие функции.

В общем случае
для n
переменных уравнение регрессии
приобретает более сложный вид.

3.
Модели линейного программирования в
решении задач автомобильных
перевозок
основные понятия,
графоаналитический и симплексный
методы

Линейное
программирование
– это наиболее разработанный раздел
математического программирования,
с помощью которого выполняются анализ
и решение экстремальных задач с
линейными связями и ограничениями.

Линейное
программирование включает в себя
целый ряд эвристических (приближенных)
методов решения, позволяющих при
заданных условиях из всех возможных
вариантов решений производственных
задач выбрать наилучший, оптимальный.
К этим методам относятся следующие –
графический, симплексный, метод
потенциалов (модифицированный
распределительный метод – МОДИ),
Хичкова, Креко, метод аппроксимации
Фогеля и другие.

Часть этих
методов объединяют общим названием
— распределительный, или транспортный,
метод.

На автомобильном
транспорте методы линейного
программирования используются с
1960-х годов для решения большого числа
важнейших производственных задач, а
именно: сокращение дальности перевозок
грузов; составление оптимальной схемы
перевозок; выбор кратчайших маршрутов
движения; задачи перевозки разных, но
взаимозаменяемых грузов; сменно-суточное
планирование; планирование перевозок
мелкопартионных грузов; распределение
автобусов по маршрутам и другие.

Особенности
модели линейного программирования
заключаются в следующем:

— целевая функция
и ограничения выражены линейными
зависимостями (равенствами или
неравенствами);

— число зависимостей
всегда меньше числа неизвестных
(условие неопределенности);

-неотрицательность
искомых переменных. Общая форма записи
модели линейного программирования в
сокращенном виде выглядит следующим
образом:

— найти х_ij
≥ 0 (j
= 1, 2…n)
при ограничениях следующего типа:

Эти ограничения
минимизируют (или максимизируют)
целевую функцию

min
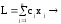
(max).

Графоаналитический
метод – это один из простейших методов
линейного программирования. Он наглядно
раскрывает сущность линейного
программирования, его геометрическую
интерпретацию. Его недостаток в том,
что он позволяет решать задачи с 2 или
3 неизвестными, т. е. применим для узкого
круга задач. Метод основан на правилах
аналитической геометрии.

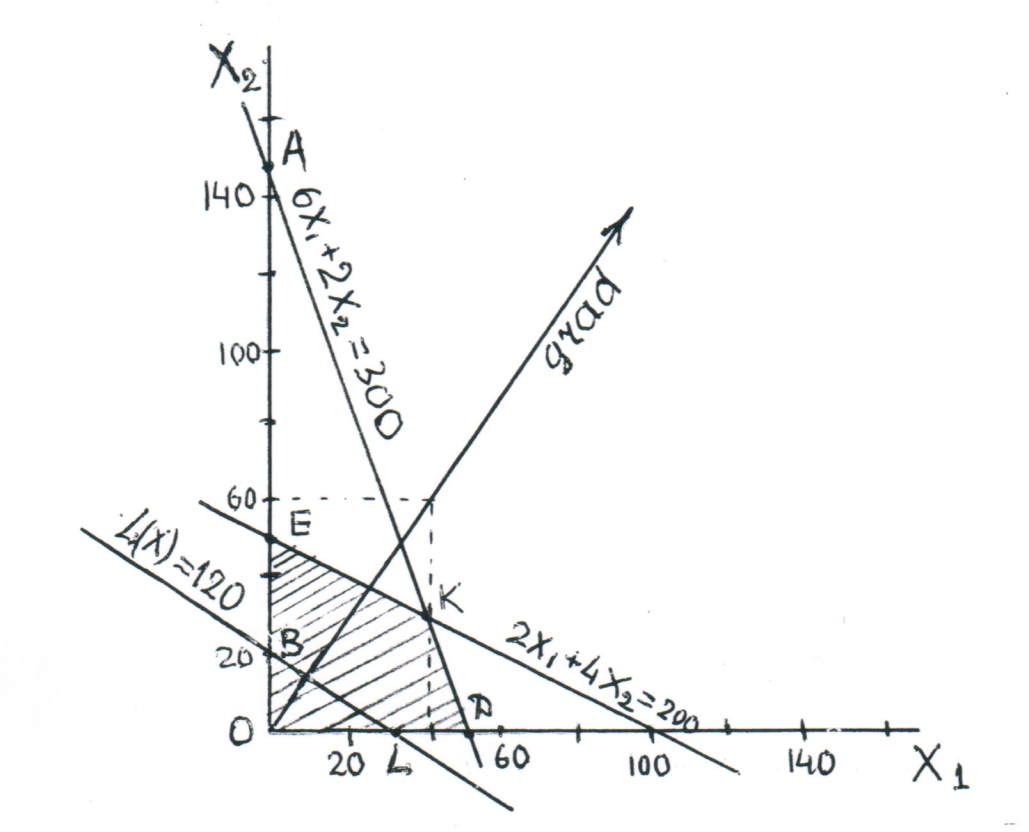
Решение задачи
с двумя переменными х₁
и х₂,
которые по смыслу задачи не должны
быть отрицательными, выполняется в
системе декартовых координат. Уравнения
х₁=0
и х₂
= 0 являются осями системы координат
первого квадранта (рис. 4).

Рис. 4. Графический
метод решения задачи по перевозке
изделий из пенобетона и стали на
максимум прибыли

Симплексный
метод –
это распространенный метод решения
задач линейного программирования.
Свое название метод получил от слова
«симплекс», обозначающего простейший
выпуклый многоугольник, число вершин
которого всегда на единицу больше,
чем размерность пространства.
Симплексный метод разработан в США
математиком Дж. Данцигом в конце 1940-х
годов.

Симплексный
метод включает получение неотрицательного
базисного решения системы канонических
линейных уравнений, последующую
минимизацию (максимизацию) целевой
функции и нахождение таким способом
оптимальных значений искомых переменных
х₁,
х_2…
х_n.

Идея симплексного
метода заключается в том, что в процессе
вычисления последовательно переходят
от первого базисного решения ко
второму, третьему и т.д. с помощью так
называемых симплексных
преобразований. Преобразования
производятся в форме симплексных
таблиц, что значительно упрощает и
ускоряет расчеты.

Чтобы получить
неотрицательные базисные решения
системы линейных уравнений, надо
процесс исключения неизвестных вести
так, чтобы свободные члены уравнений
на всех этапах процесса оставались
неотрицательными. При этом следует
руководствоваться следующим правилом:
в качестве новой базисной переменной
принимается любая свободная

переменная, при
которой есть хотя бы один положительный
коэффициент; выводится из базиса
переменная, которая соответствует
наименьшему отношению свободных
членов уравнений к соответствующим
положительным коэффициентам уравнений
при вводимой в базис переменной. Такие
преобразования называются симплексными
преобразователями.

Это очень важно,
поскольку для нахождения частного
неотрицательного решения, отвечающего
наибольшему возможному значению
какой-то одной свободной переменной
при нулевых значениях других свободных
переменных, вместо определения области
изменения указанной переменной и
подстановки ее наибольшего возможного
значения в общее решение достаточно
принять эту переменную за базисную и
подвергнуть систему симплексному
преобразованию, перейдя к новому
базису, что значительно упрощает
расчеты.

Вычисления удобно
производить с помощью симплексных
таблиц. Переход от одной таблицы к
другой соответствует одной итерации,
т. е. переходу от одного базиса к
другому, при этом значение целевой
функции уменьшается. За определенное
число итераций переходят к базису,
для которого получают оптимальное
(минимальное или максимальное) значение
целевой функции. Рассмотрим симплексный
метод в общем виде.

Общая задача
линейного программирования заключается
в минимизации (максимизации) целевой
функции, переменные которой связаны
между собой системой линейных уравнений,
подчинены условию неотрицательности.

Основные правила
симплексного метода линейного
программирования (при решении задачи
на минимум):

1) систему
ограничений задачи линейного
программирования необходимо решить
относительно какого-либо базиса.
Выразить целевую функцию через
свободные переменные;

2) составить
симплексную таблицу. Если в индексной
строке все элементы отрицательны, то
базисное решение оптимально. Задача
решена;

3) если в индексной
строке симплекс-таблицы есть
положительные элементы, то столбец,
соответствующий минимальному из них,
принимается за разрешающий. Составляются
отношения элементов столбца свободных
членов к положительным элементам
разрешающего столбца. Строка,
соответствующая минимальному из этих
отношений, является разрешающей.
Элемент таблицы, находящийся на
пересечении разрешающего столбца и
разрешающей строки, называется
разрешающим;

4) переходить к
новому базису следует, исключая из
старого базиса переменную, соответствующую
разрешающей строке, вводя вместо нее
переменную, которая соответствует
разрешающему столбцу. Составляется
новая симплекс-таблица, соответствующая
новому базису.

4.
Маршрутизация перевозок помашинными
отправками основные этапы
решения задач

При помашинных
отправках грузов каждый отдельный
автомобиль загружается только в адрес
одного потребителя. Сменно-суточное
планирование таких перевозок занимает
одно из центральных мест в задачах
маршрутизации и включает составление
маршрутов движения подвижного состава
и порядок его следования между
корреспондирующими точками. Оптимальное
планирование рассматриваемой задачи
позволяет получать значительный
экономический эффект.

Первым шагом
работы по составлению рациональных
маршрутов является классификация
грузов, предъявляемых к перевозке, на
группы, однородные с точки зрения
возможности их перевозки на одном и
том же подвижном составе.

Маршруты
составляются по каждой группе грузов.

Практика решения
задач по маршрутизации перевозок
грузов учитывает множество ограничений,
вызываемых конкретными условиями
работы грузовых точек и автомобильного
транспорта. К ним относятся: заданное
множество пунктов отправления и
получения грузов; объемы грузооборота
у поставщиков и потребителей; характер
груза, время доставки, структура и
наличие парка подвижного состава;
мощность и размещение автотранспортных
предприятий; режимы работы водителей
и так далее.

Многообразие
ограничений в каждом конкретном случае
привело к созданию различных методов
маршрутизации, в том числе и эвристических,
базирующихся на материалах опыта
прошлой работы. Имеется большое число
методов маршрутизации массовых грузов,
когда грузы перевозятся помашинными
отправками, используются сложные
алгоритмы решения задач.

В настоящем
разделе рассмотрен один широко
используемый метод маршрутизации –
метод
совмещенных планов.
Метод используется на базе линейного
программирования. Основной задачей
сменно-суточного планирования является
составление такого плана работы
транспортных средств на данную смену,
который позволит выполнить заданные
перевозки в установленные сроки
минимальным количеством автомобилей.
Достигается это при максимальной
производительности подвижного состава,
которая в общем виде выражается
формулой:

,
(1)

где Р –
производительность автомобиля за
смену, т·км; Т_н
– время в наряде, ч; g
–грузоподъемность автомобиля, т; γ –
коэффициент использования
грузоподъемности; β – коэффициент
использования пробега; V_т
– техническая скорость, км/ч; l_г
– расстояние перевозки груза, км; t_пр
–простой автомобиля при погрузке и
выгрузке, ч.

Воздействуя на
указанные технико-эксплуатационные
показатели, можно увеличить
производительность подвижного состава.

Из всех вышеуказанных
факторов от качества сменно-суточного
планирования на автотранспортном
предприятии в наибольшей степени
зависит коэффициент использования
пробега.

Таким образом,
задача ежедневного планирования
перевозок грузов на автотранспортном
предприятии формируется как задача
обеспечения заданного объема перевозок
грузов с наименьшим порожним пробегом
автомобиля.

Эта задача
маршрутизации состоит в следующем.

Разнородный груз
сосредоточен в пунктах отправления
А₁,
А₂…А_i…А_m
в количествах соответственно а₁,
a₂…a_i…a_m
единиц. Его необходимо доставить в
пункты назначения В₁,
В₂…В_j…В_n
в количествах в₁,
в₂…в_j…в_n
соответственно.

Объём перевозок
из i-го
пункта отправления в j-й
пункт назначения составляет q_ij
единиц и известен для всех пунктов.

Расстояние
от i-го
пункта отправления до j-го
пункта назначения равно l_ij
и известно для всех комбинаций ij.

В процессе
выполнения перевозок в пунктах
назначения В₁,
В₂…В_j…В_n
после разгрузки автомобилей будет
образовываться порожняк в количествах
в₁¹,
в₂¹…в_j¹…в_n¹
единиц.

Этот порожняк
необходимо подать под очередную
загрузку в пункты отправления А₁,
А₂…А_i…А_m
в количестве а₁¹,
а₂¹…а_i¹…а_m¹.

Величины а_i,
в_j,
q_ij,
a_i¹,
в_j¹
могут выражаться либо в тоннах, либо
в ездках автомобиля. Для существа
задачи это безразлично, тем более что
тонны всегда можно перевести в ездки.
Однако с методической точки зрения
удобнее пользоваться ездкой автомобиля
с грузом и без груза.

Количество
прибывающих в пункт назначения гружёных
автомобилей представляет ресурсы
порожняка в данном пункте. Количество
убывающих из пункта отправления
гружёных автомобилей – потребность
этого пункта в порожняке.

По смыслу
рассматриваемой задачи всегда имеет
место условие:

в_j¹
= в_j=
,
где j=1,
2…n;

a_i¹
= a_i
=
,
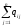
где i=1,2…m.

Расстояние
от В_j
до А_i_,
равное l_ji=l_ji_,
известно для всех сочетаний i,
j.

За смену каждый
автомобиль выполняет несколько ездок
с грузом из одного или нескольких
пунктов отправления в один или несколько
пунктов назначения. После каждой ездки
с грузом автомобиль возвращается в
пункт отправления порожняком. Из
каждого пункта назначения автомобиль
может следовать под погрузку в любой
пункт отправления, имеющий груз.

Дополнительным
условием задачи является требование,
чтобы за рабочую смену автомобиль
направлялся не более чем в 4 разных
пункта отправления и такое же количество
пунктов назначения. Практически это
означает, что при сменном задании с
большим числом ездок необходимо
составлять кольцевой маршрут так,
чтобы по нему можно было сделать
несколько оборотов.

Таким образом,
требуется составить такой план
перевозок (маршруты движения автомобилей
и сменные задания водителям), который
обеспечит выполнение заданных объёмов
перевозок с наименьшим холостым
пробегом автомобилей.

5.
Методы определения кратчайших
расстояний перевозок

Табличный метод:

Если два пункта
находятся в пределах видимости, то
кратчайший путь между ними можно
выбрать, не применяя никаких вычислений.
Когда пункты достаточно удалены друг
от друга, то возникают различные
варианты передвижения, которые
необходимо сравнивать, чтобы выбрать
наилучший.

На рис. 5 представлена
модель участка транспортной сети,
сформированная на основе карты
экономического региона.

Задача о нахождении
кратчайшего пути между пунктами (рис.
5) может быть в общем виде сформулирована
на основе положений графов следующим
образом. Дан граф

G
= (x,
y).

Каждому ребру
графа приписано некоторое число (длина
ребра) lij
≥ 0. Тогда любая цепь μ, составленная
из нескольких ребер, характеризуется
длиной l_μ.
Требуется для двух произвольных вершин
найти такой путь, чтобы его длина была
наименьшей:

Рис. 5. Определение
кратчайших расстояний по транспортной
сети

методом потенциалов

Пусть задана
транспортная сеть, состоящая из пунктов
А₁,
А_2…,
А_i_…,
А_m
и дорог,
соединяющих эти пункты между собой.
Длины участков дороги между каждой
парой соседних пунктов А_i
Аj
известны
и равны l_jj.
Если два соседних пункта А_i
и
Аj
непосредственно
не соединены
между собой участком дороги, то
принимаем l_jj=
∞. Из начального пункта А₁в

конечный пункт
А_m
можно попасть по большому числу
маршрутов, проходящих через разные
промежуточные пункты. Требуется найти
среди этих маршрутов путь наименьшей
протяженности.

Переведём задачу
на формальный язык. Обозначим каждый
участок сети между двумя соседними
пунктами А_i
и Аj
числом x_ij=
1, если он является звеном выбранного
маршрута движения из А_iв А_m_,
и x_ij=0,
если он не входит в этот маршрут. Тогда
задача отыскания кратчайшего пути из
А_i
в А_m
сводится к выбору чисел x_ij
(i,
j
= 1, 2, …, m),
при которых достигает минимума линейная
форма

,
(6.3)

при условии

i=2, 3, …, m-1;
(6.4)

;
(6.5)

;
(6.6)

x_ij
≤1, i, j
=1,2………….m
(6.7)

Линейная форма
(6.3) определяет длину маршрута между
начальным и конечным пунктами. Условия
(6.4) означают, что для любого 0≤пункта
маршрута А_i,
исключая начальный и конечный, число
дорог, входящих в этот пункт, равно
числу дорог, выходящих из него. Поскольку
l_ji>0
для всех I
и j,
условия (6.4) вместе с требованием
минимизации линейной формы (6.3) означают,
что из каждого пункта Аi
(i=2,
3, …, m
-1) выходит не более одной дороги.
Условия (6.5) фиксируют тот факт, что
количество дорог, выходящих из
начального пункта маршрута, Аi
превышает на единицу число дорог,
входящих в этот пункт. Аналогично
условия (6.6) указывает на то, что в
последний пункт А_mвходит
на одну дорогу больше, чем выходит.
Условия (6.5) и (6.6) вместе с условиями
(6.4) и требованием минимизации линейной
формы (6.3) означают, что в каждый пункт
маршрута входит ровно одна дорога и
из каждого пункта маршрута исходит
ровно одна дорога. Наконец, условия
(6.7) требуют, чтобы все x_ij
были равны нулю или единице. В целом,
соотношения (6.3-6.7) представляют собой
определение кратчайшего пути на сети
дорог между двумя заданными пунктами,
т.е. аналитическую модель рассматриваемой
задачи.

Параметры l_ji при
необходимости могут означать не только
расстояния, но и продолжительности
проезда по участкам сети или стоимость
пробега автомобиля.

Поскольку условия
задачи записаны в виде линейных
уравнений и неравенства, а критерий
показателя качества решения выражается
линейно, сформулированная задача
является задачей линейного
программирования. Рассмотрим процесс
решения этой задачи с помощью метода
потенциалов.

Общая вычислительная
схема применительно к данной задаче
следующая. В специальную таблицу
(табл. 4) типа «шахматной»

Таблица
4

Базовая
таблица. расчета расстояний между
пунктами и индексов U
и V

Пункт	Вспомо- гатель- ные	Пункт
А₁	А₂	…	Аj	…	А_m
Строка Столбец	υ₁	υ₂	…	υ_j	…	υ_m
А₁	u₁	l₁₁	l₁₂	…	l₁_j	…	l₁_m
А₂	u₂	l₂₁	l₂₂	…	l₂_j	…	l₂_m
…	…	…	…	…	…	…
А_i	u_i	l_i₁	l_i₂	…	l_ij	…	l_im
…	…	…	…	…	…	…	…
А_m	u_m	l_m₁	l_m₂	…	l_mj	…	l_mm

заносят расстояния
l_ji
от каждого пункта Аi
((i=1,
2, …, m
) до всех соседних с ним пунктов Аi
((i=1,
2, …, m
). После этого для каждого пункта Аi
и Аj
рассчитывают индексы u_i
и υ_j
следующим образом. Индекс u_i принимают
равным нулю (u_i=0). Затем
по порядку, начиная с первой строки
таблицы, рассматривают клетки с
заполненными l_ji
. Если для некоторой заполненной клетки
(I,
j)
индекс u_i
уже известен, а υ_j — ещё нет,
то определяют υ_j
по формуле

υ_j=
u_i₊
l_ji.
(6.8)

Если при определении
очередного υ_j в i-м
столбце имеется более одной клетки с
записанными l_ji
и известными u_i, то
принимают

υ_j= min
(u_i₊
l_j)
.
(6.9)

Найденные значения
υ_j
записывают в соответствующие клетки
вспомогательной строки, а также в
клетки вспомогательного столбца,
исходя из правила: u₁=
υ₁,
u₂=
υ₂,
… u_m=
υ_m.
После определения всех индексов υ_j
и u_i
проверяют оптимальность данного
решения, сравнивая все l_ji
с их разностями (υ_j—
u_i).
Если для всех заполненных клеток
соблюдается условие

l_ij
≥υ_j—
υ_j_,

(6.10)

то решение
оптимально и каждое найденное число
υ_j
дает кратчайшее расстояние от пункта
А₁
до соответствующего пункта А_i,
до соответствующего пункта Аj
(i=1,2,…m).
При

наличии хотя бы
одной клетки с величиной l_ij
<υ_j—
u_i
решение неоптимально и вычисления
необходимо продолжить.

Предположим, что
в клетке Аi
_n
Аj
_n
нарушено условие оптимальности (6.10),
т.е.

li _njn<
υ i _n—
ui _n.

В этих условиях
необходимо изменить решение следующим
образом. Индекс υ
_j
_n
заменяют индексом υ`
i
_n
, величину которого определяют по
формуле

υ i _n=
υ i _n+
li _njn.

На каждой итерации
корректируют индексы υ_j
у всех клеток с l_ij<
υ_j—
u_i_,
после чего решение снова проверяют
на оптимальность. Вычисления повторяют
до тех пор, пока в таблице не будет
выполнено условие оптимальности
(6.10).

При определении
кратчайших расстояний от пункта А₂
до всех остальных принимают u₂=0,
после чего находят все индексы и
выполняют все описанные выше вычисления.
При определении кратчайших расстояний
от пункта А₃
до всех остальных принимают u₃=0
и т.д.

6.
Методы планирования перевозок по
сборно — развозочным маршрутам

Оптимизация
мелкопартионных перевозок грузов,
когда размер отправляемой или получаемой
партии груза существенно меньше
грузовместимости используемых
автотранспортных средств, является
очень важной среди задач планирования
грузовых автомобильных перевозок.

При этих перевозках
автомобили функционируют на развозочных,
сборных, развозочно-сборных (далее
развозочных) маршрутах в составе
комплекса различных автотранспортных
систем (РСТС). Используется классификация
систем по комплексу признаков
(выполняемая функция, конфигурация
системы, мощность грузопотоков,
количество пунктов погрузки-выгрузки
и подвижного состава и другие). Все
РСТС делятся на 9 видов.

1.
Развозочная
S_p
– система, состоящая из пункта погрузки,
множества пунктов разгрузки, транспортных
связей между ними и одного автомобиля,
осуществляющего доставку груза.
Технологическая схема доставки груза
представляет собой развозочный
маршрут.

2.
Сборная S_с
– система, состоящая из множества
пунктов погрузки, пункта разгрузки,
транспортных связей между ними и
одного автомобиля, осуществляющего
доставку груза. Технологическая схема
доставки груза представляет собой
сборный
маршрут.

3.
Развозочно-сборная
S_pc
– система, представляющая собой
совокупность предыдущих транспортных
систем, включающая в себя множество
пунктов погрузки и разгрузки,
транспортных связей между ними и один
автомобиль, осуществляющий доставку
груза. Технологическая схема доставки
груза представляет собой развозочно-сборный
маршрут.

4. Простая S_п
– система, состоящая из множества S_p
(S_с
или S_pc),
в которой осваиваются, по сравнению
с предыдущими системами, большие
грузопотоки.

Примером S_п
служит сбор и вывоз бытовых отходов
на ассполя, сбор писем из абонентских
ящиков автомобилями в отделения связи,
сбор и вывоз пищеотходов, доставка по
магазинам продукции бытовой химии,
доставка мебели из магазинов населению
и другие.

5. Развозочная
с центром погрузки S_рц
– система, состоящая из совокупности
S_p,
в которой осваиваются, по сравнению
с S_p,
большие грузопотоки.

Пример
функционирования S_рц
— развоз газа в цистернах; развоз
стеновых панелей с домостроительного
комбината потребителям, раствора и
другие.

6. Сборная с
центром разгрузки S_сц
– система, состоящая из совокупности
S_с,
в которой осваиваются, по сравнению
со сборной системой, большие грузопотоки.

Пример
функционирования S_сц
– сбор и вывоз бытовых отходов на
мусороперерабатывающий (сжигающий)
завод, сбор и вывоз строительного
мусора по системе «несменяемых»
контейнеров.

7. Комбинированная
первого вида S_к1
– система,
состоящая из центрального пункта с
несколькими фронтами погрузки
(разгрузки и погрузо-разгрузки) и
множества предыду

щих транспортных
систем (кроме простой системы S_п),
в которой по условиям перевозок
работают несколько единиц или даже
десятков автомобилей.

8.
Комбинированная
второго вида S_к2
– система,
состоящая из центрального и множества
периферийных пунктов погрузки и
разгрузки, транспортных связей между
ними и автомобилей, осуществляющих
доставку груза.

Примером системы
являются развоз и сбор почтовых
отправлений, посылок, журналов и других
почтовых грузов в отделения связи;
развоз продукции в таре из хлебо- и
молокозаводов и сбор возвратной тары
в них; развоз мелкоштучных и
контейнеропригодных грузов в контейнерах
и на поддонах на строительные объекты
и сбор возвратной тары.

9. Город-регион
S_r_—_p–
это система, состоящая из множества
РСТС, приведенных выше, в которой по
условиям перевозок работают несколько
десятков и даже сотен автомобилей
автотранспортного предприятия.

Для
грузовых перевозок можно отметить
следующие: метод перебора вариантов
маршрута; метод сумм; метод «ветвей и
границ»; Кларка-Райта и другие. Для
пассажирских перевозок — метод Б.Л.
Геронимуса и другие.

Необходимость
учета при проектировании РСТС
многочисленных требований и ограничений,
часто противоречащих друг другу,
особенностей функционирования реальных
РСТС; выполнение значительного
количества вычислительных процедур
приводят к необходимости использования
ЭВМ. Это обусловливает необходимость
разработки обобщенного алгоритма
проектирования РСТС, учитывающего
особенности решения задачи проектирования
для различных РСТС.

Метод перебора
вариантов.

Число перестановок
из w
пунктов завоза (вывоза), включаемых в
маршрут по w
пунктам:

Pw
= w!,
(8.1)

где w!
– факториал целого положительного
числа w,
который равен произведению: w!
= 1·2·3…· w.
При трех пунктах груза количество
возможных маршрутов М
= w!
= 3! = 1·2·3 = 6, таким образом, возможны
шесть маршрутов доставки груза из
пункта А
(см. табл.
5). Выбор маршрута осуществляется по
критерию «минимум затрат», чему
соответствует минимум пробега. При
наличии двух и более маршрутов
одинаковой протяженности цели системы
соответствует минимум грузооборота
на маршруте.

Таблица
5

Результаты
расчета пробега и грузооборота в
развозочной системе

Номер маршрута	Маршрут	Пробег, км	Грузообот, т·км
1	А—В₁—В₂—В₃—А	29,0	46,0
2	А—В₃—В₂—В₁—А	29,0	70,0
3	А—В₁—В₃—В₂—А	33,0	56,0
4	А—В₂—В₃—В₁—А	33,0	76,0
5	А—В₂—В₁—В₃—А	34,0	61,0
6	А—В₃—В₁—В₂—А	34,0	75,0

Рассмотренный
пример – с числом пунктов завоза w
= 3. Что будет, если потребителей 4, или
5, или 10? Согласно формуле (8.1) число
вариантов маршрутов, которые необходимо
будет рассмотреть, обсчитать и т.д.,
будет равно соответственно 24; 120;
3628800. Решение задачи с числом пунктов
завоза более четырех рассмотренным
способом в оперативном режиме
нерационально.

Проектирование
маршрутов методом сумм

Метод сумм
является одним из наиболее простых
приближенных методов решения задачи
рационального объезда точек на маршруте
(эта задача еще называется задачей
коммивояжера).

Все пункты
называются вершинами сети, а линия,
соединяющая две соседних вершины, —
звеном. Незамкнутая сеть, связывающая
две и более вершины с минимальной
суммарной длиной всех соединяющих их
звеньев, называется кратчайшей
связывающей сетью.

На транспортной
сети находят наименьшее звено. Затем
рассматривают все звенья, связанные
с одной из своих вершин с выбранным
звеном.

При этом нельзя
выбирать звено, соединяющее две ранее
включенные в сеть вершины.

Далее опять
рассматривают все звенья, связанные
с вершинами полученной сети, и из них
выбирают наименьшее и так далее до
тех пор, пока не будет выбрана сеть.

Далее все пункты
маршрута, начиная с А,
связываются такой замкнутой линией,
которая соответствует кратчайшему
пути объезда этих пунктов. Первоначально
при использовании метода сумм строится
таблица, называемая симметричной
матрицей.

По главной
диагонали в ней расположены пункты,
включаемые в маршрут. Дополнительно
в этой матрице имеется итоговая строка
– строка сумм. В ней проставляют сумму
расстояния по каждому столбцу. Затем
строят начальный маршрут из трех
пунктов, имеющих максимальную сумму
по своему столбцу. Принимаем маршрут.
В него включают следующий пункт с
максимальной суммой. Чтобы определить,
между какими пунктами его следует
вставить, надо поочередно включать
этот пункт между каждой парой. При
этом для каждой пары этих пунктов
находят величину прироста пробега
автомобиля на маршруте при

включении в
начальный маршрут вновь выбранного
пункта. Величину этого прироста ∆_крнаходят
по формуле

∆_кр
= L₁₃
+ L₂₃
– L₁₂,

(2)

где L
– расстояние; 1 – первый соседний
пункт; 2 – второй соседний пункт; 3 –
включаемый пункт.

7.
Понятие о теории массового обслуживания
в решении задач автомобильных
перевозок

Теория массового
обслуживания является одним из разделов
теории вероятностей. В последние годы
она получила развитие и выделилась в
самостоятельный раздел математики.
Основоположником теории массового
обслуживания является датский ученый
А.К. Эрланг. Его первая работа по этому
вопросу была опубликована в 1909 году.

Идеи и методы
теории массового обслуживания в
настоящее время получают широкое
распространение на автомобильном
транспорте. Используя теорию массового
обслуживания, можно находить оптимальные
и близкие к оптимальным решения таких
практических задач, как определение
числа постов погрузки, выгрузки и
технического обслуживания, оптимизация
процесса заправки автомобилей топливом,
определение величины резерва подвижного
состава, выбор количества подвижного
состава, обслуживание населения
автомобилями-такси и другие.

Термин массовое
обслуживание
означает, что речь идет не о конкретном
объекте, а о совокупности объектов,
потребности которых требуется
удовлетворить.

Особенностью
теории массового обслуживания является
то, что она рассматривает любой процесс
массового обслуживания как вероятностный.
Теория массового обслуживания
занимается изучением таких транспортных
процессов, в которых возникают очереди
на обслуживание. Причинами возникновения
очередей являются случайно изменяющиеся
потребности в обслуживании, вызываемые,
например, неравномерным прибытием
автомобилей на погрузку–выгрузку;
ограниченностью мощности
погрузо-разгрузочных постов;
неравномерным прибытием автомобилей
на заправку топливом, на станцию
технического обслуживания и
ограниченностью мощности постов
обслуживания; прибытие такси по
вызову; подход пассажиров к
остановкам городского транспорта;
прибытие транспортных средств к
пассажирским остановкам и так далее.

С помощью теории
массового обслуживания решаются
задачи оптимизации вышеуказанных
процессов.

Общая модель
системы массового обслуживания состоит
из обслуживаемой и обслуживающей
систем. Обслуживаемая система включает
совокупность источников требований
и входящего потока требований.

Требование –
это запрос на выполнение работы
(погрузки-выгрузки, заправки топливом,
ремонта, посадки в транспорт для
поездки и другие).

Источник требований
– это объект (диспетчер, водитель,
пассажир, механизм и так далее), который
может послать в обслуживающую систему
только одно требование.

Носитель
требований, например водитель,
автомобиль или агрегат, которому могут
понадобиться услуги, запасные части,
житель города, которому понадобилось
свободное такси. Требования и его
носитель часто отождествляются.
Требования от всех источников в
обслуживающую систему образуют
входящий поток требований.

Обслуживающая
система состоит из накопителя и
механизма обслуживания. Требования
поступают в накопитель, где ожидают
начала обслуживания, если есть очередь,
или обслуживаются сразу.

Обслуживанием
считается удовлетворение поступившего
запроса на выполнение услуги. Механизм
обслуживания состоит из нескольких
обслуживающих аппаратов.

Обслуживающий
аппарат – это часть механизма
обслуживания, способная удовлетворить
только одно требование. После окончания
обслуживания требования покидают
систему, образуя выходящий поток
требований.

Для применения
теории массового обслуживания нужно
изучать и анализировать фактические
данные. Практическая цель применения
теории – это предсказание поведения
системы при ее будущей работе еще до
того, как система создана, то есть на
стадии проектирования системы.

Основной базовой
величиной в теории обслуживания
является поток требований на
обслуживание. Для рассматриваемых
автотранспортных процессов потоки в
большинстве случаев принимаются
стационарными
(не зависящими от начала отсчета
времени, а зависящими только от его
продолжительности), ординарными
(когда в любой момент времени поступает
только одно требование) и потоками
без последствий
(не зависящими от количества ранее
поступивших требований). Такие потоки
называются простейшими.

Работа
погрузочно-разгрузочных постов, постов
на станциях технического обслуживания,
на топливо — заправочных пунктах,
обслуживающих подвижной состав,
относится к разомкнутым системам. В
таких системах отсутствует связь
между обслуженным требованием и
требованиями, поступившими на
обслуживание.

При этом выбор
наиболее эффективного варианта
загрузки системы является проблематичным.
Исходить из средней загруженности
системы нельзя, поскольку одним из
условий нормальной работы системы
является выполнение на каждой фазе
работы неравенства

<
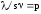
1,
(3)

где λ – средняя
интенсивность входящего потока
требований; ν – интенсивность
обслуживания одним аппаратом в единицу
времени; s
–число обслуживающих аппаратов; p
– коэффициент использования
обслуживающей системы.

Если коэффициент
использования p
будет больше единицы, то обслуживающая
система не справится с обслуживанием
и очередь будет неограниченно расти.

В соответствии
с поведением требований системы
подразделяются на три группы:

Система с
отказами, в которых требование,
заставшее обслуживающие аппараты
занятыми, получает отказ и теряется.
Например, автомобиль уезжает со
станции технического обслуживания,
если посты заняты;

2. Система с
ожиданиями, например, автомобиль
ожидает погрузки;

3. Смешанные
системы, например, часть автомобилей
уезжает с автозапра- вочной станции,
если очередь на заправку велика.

Теория массового
обслуживания позволяет определить
оптимальный характер функционирования
системы массового обслуживания по
характеристикам ее частей.

Задача № 1

По исходным
данным составим матрицу условий (табл.
6). В правых верхних углах клеток,
представляющих собой реальные маршруты
перевозок, указаны расстояния между
соответствующими пунктами.

Составим
данный исходный план в табл. 7.

Таблица 6
Матрица условий
Пункт назначения	Вспомогательные	Пункт назначения	Наличие груза, т.
Строка Столбец	B₁	B₂	B₃	B₄	B₅	B₆

А₁		5	8	13	6	9	4	5
А₂		12	7	11	10	6	8	10
А₃		9	10	7	6	10	7	15
А₄		8	12	4	13	5	9	20
Потребность в грузе, т.	6	5	9	6	14	10	50

Таблица 7
Данный исходный план
Пункт назначения	Вспомогательные	Пункт назначения	Наличие груза, т.
Строка Столбец	B₁	B₂	B₃	B₄	B₅	B₆
V₁= 6	V₂= 1	V₃= -1	V₄= 3	V₅= 0	V₆= 4
А₁	U₁= 0		5		8		13		6		9	4	5
										5
А₂	U₂= 6		12		7		11		10		6	8	10
2		5						3
А₃	U₃= 3		9		10		7		6		10	7	15
4						6				5
А₄	U₄= 5		8		12		4		13		5	9	20
				9				11
Потребность в грузе, т.	6	5	9	6	14	10	50

Транспортные
расходы составят:

z = 5 ∙
4 + 2 ∙ 12 + 5 ∙ 7 + 3 ∙ 6 + 4 ∙ 9 + 6 ∙ 6 + 5 ∙ 7 + 9
∙ 4 + 11 ∙ 5 = 295

Решим задачу
методом потенциалов. Т.к. m+n-1= 6 + 4 – 1 =
9 и имеем 9 загруженных клеток, план
ацикличный. Пусть U_i
и V_j
— потенциалы i-го склада и j-го магазина
соответственно.

Полагая потенциал
U₁=0,
определяем остальные потенциалы из
соотношения U_i+V_j=C_i,j,
просматривая все занятые клетки.
Получим:

U₁=0

V₆=C_1,6
– U₁=
4

U₃= C_3,6
– V₆= 3

V₁= C_3,1– U₃= 6

U₂= C_2,1– V₁= 6

V₂
= C_2,2–
U₂=
1

V₄=
C_3,4—
U₃=
3

V₅=
C_2,5–
U₂
= 0

U₄=
C_4,5–
V₅=
5

V₃
= C_4,3– U₄
= -1

Для свободных
клеток определим значения оценок
(разностей между прямыми и косвенными
тарифами).

S_1,1=
С_1,1
— (U₁
+ V₁)
= -1

S_1,2=
С_1,2—
(U₁
+ V₂)
= 7

S_1,3=
С_1,3—
(U₁
+ V₃)
= 12

S_1,4=
С_1,4—
(U₁
+ V₄)
= 3

S_1,5=
С_1,5—
(U₁
+ V₅)
= 9

S_2,3=
С_2,3—
(U₂
+ V₃)
= 6

S_2,4=
С_2,4—
(U₂
+ V₄)
= 1

S_2,6=
С_2,6—
(U₂
+ V₆)
= -2

S_3,2=
С_3,2—
(U₃
+ V₂)
= 6

S_3,3=
С_3,3—
(U₃
+ V₃)
= 5

S_3,5=
С_3,5—
(U₃
+ V₅)
= 7

S_4,1=
С_4,1
— (U₄
+ V₁)
= -3

S_4,2=
С_4,2—
(U₄
+ V₂)
= 6

S_4,4=
С_4,4—
(U₄
+ V₄)
= 5

S_4,6=
С_4,6—
(U₄
+ V₆)
= 0

Имеем три клетки с отрицательными
оценками – (1,1), (2, 6) и (4, 1). Выбираем
клетку с наименьшей оценкой (4, 1) и
строим для нее цикл табл. 8.

Таблица 8
Допустимый исходный план
Пункт назначения	Вспомогательные	Пункт назначения	Наличие груза, т.
Строка Столбец	B₁	B₂	B₃	B₄	B₅	B₆
V₁= 6	V₂= 1	V₃= -1	V₄= 3	V₅= 0	V₆= 4
А₁	U₁= 0		5		8		13		6		9	4	5
										5
А₂	U₂= 6	—	12		7		11		10	+	6	8	10
2		5						3
А₃	U₃= 3		9		10		7		6		10	7	15
4						6				5
А₄	U₄= 5	+	8		12		4		13	—	5	9	20
				9				11
Потребность в грузе, т.	6	5	9	6	14	10	50

Перемещаем по
циклу груз величиной в 2 единицы,
прибавляя эту величину к грузу в
клетках со знаком «плюс» и отнимая
ее от груза в клетках со знаком «минус».
В результате перемещения по циклу
получим новый план:

Таблица 9
Допустимый исходный план
Пункт назначения	Вспомогательные	Пункт назначения	Наличие груза, т.
Строка Столбец	B₁	B₂	B₃	B₄	B₅	B₆
V₁= 6	V₂= 4	V₃= 2	V₄= 3	V₅= 3	V₆= 4
А₁	U₁= 0		5		8		13		6		9	4	5
										5
А₂	U₂= 3		12		7		11		10		6	8	10
		5						5
А₃	U₃= 3		9		10		7		6		10	7	15
4						6				5
А₄	U₄= 2		8		12		4		13		5	9	20
2				9				9
Потребность в грузе, т.	6	5	9	6	14	10	50

Целевая функция
(транспортные расходы) z = 289. Значение
целевой функции изменилось на 6 единиц
по сравнению с предыдущим этапом.

Проверим полученный
план на оптимальность. Подсчитаем
потенциалы.

U₁=0

V₆=C_1,6
– U₁=
4

U₃=
C_3,6
– V₆=
3

V₁=
C_3,1–
U₃=
6

V₄=
C_3,4—
U₃=
3

U₄=
C_4,1–
V₁=
2

V₃
= C_4,3–
U₄
= 2

V₅=
C_4,5–
U₄
= 3

U₂=
C_2,5–
V₅=
3

V₂
= C_2,2–
U₂=
4

Для свободных
клеток определим значения оценок
(разностей между прямыми и косвенными
тарифами).

S_1,1=
С_1,1
— (U₁
+ V₁)
= -1

S_1,2=
С_1,2—
(U₁
+ V₂)
= 4

S_1,3=
С_1,3—
(U₁
+ V₃)
= 11

S_1,4=
С_1,4—
(U₁
+ V₄)
= 3

S_1,5=
С_1,5—
(U₁
+ V₅)
= 6

S_2,1=
С_2,1—
(U₂
+ V₁)
= 3

S_2,3=
С_2,3—
(U₂
+ V₃)
= 6

S_2,4=
С_2,4—
(U₂
+ V₄)
= 4

S_2,6=
С_2,6—
(U₂
+ V₆)
= 1

S_3,2=
С_3,2—
(U₃
+ V₂)
= 3

S_3,3=
С_3,3—
(U₃
+ V₃)
= 2

S_3,5=
С_3,5—
(U₃
+ V₅)
= 4

S_4,2=
С_4,2
— (U₄
+ V₂)
= 6

S_4,4=
С_4,4—
(U₄
+ V₄)
= 8

S_4,6=
С_4,6—
(U₄
+ V₆)
= 3

Имеем клетку (1,
1) с отрицательной оценкой, план не
оптимален. Строим для этой клетки
цикл.

Таблица 10
Допустимый исходный план
Пункт назначения	Вспомогательные	Пункт назначения	Наличие груза, т.
Строка Столбец	B₁	B₂	B₃	B₄	B₅	B₆
V₁= 6	V₂= 4	V₃= 2	V₄= 3	V₅= 3	V₆= 4
А₁	U₁= 0	+	5		8		13		6		9	—	4	5
										5
А₂	U₂= 3		12		7		11		10		6		8	10
		5						5
А₃	U₃= 3	—	9		10		7		6		10	+	7	15
4						6				5
А₄	U₄= 2		8		12		4		13		5		9	20
2				9				9
Потребность в грузе, т.	6	5	9	6	14	10	50

Перемещаем по
циклу груз величиной в 4 единиц,
прибавляя эту величину к грузу в
клетках со знаком «плюс» и отнимая
ее от груза в клетках со знаком «минус».
В результате перемещения по циклу
получим новый план:

Таблица 11
Допустимый исходный план
Пункт назначения	Вспомогательные	Пункт назначения	Наличие груза, т.
Строка Столбец	B₁	B₂	B₃	B₄	B₅	B₆
V₁= 5	V₂= 3	V₃= 1	V₄= 3	V₅= 2	V₆= 4
А₁	U₁= 0		5		8		13		6		9	4	5
4										1
А₂	U₂= 4		12		7		11		10		6	8	10
		5						5
А₃	U₃= 3		9		10		7		6		10	7	15
						6				9
А₄	U₄= 3		8		12		4		13		5	9	20
2				9				9
Потребность в грузе, т.	6	5	9	6	14	10	50

Целевая функция
(транспортные расходы) z = 285. Значение
целевой функции изменилось на 4 единицы
по сравнению с предыдущим этапом.

Проверим полученный
план на оптимальность. Подсчитаем
потенциалы.

U₁=0

V₁= C_1,1– U₁= 5

U₄=
C_4,1–
V₁=
3

V₃
= C_4,3–
U₄
= 1

V₅=
C_4,5–
U₄
= 2

U₂=
C_2,5–
V₅=
4

V₂
= C_2,2–
U₂=
3

V₆=C_1,6
– U₁=
4

U₃=
C_3,6
– V₆=
3

V₄=
C_3,4—
U₃=
3

Для свободных
клеток определим значения оценок
(разностей между прямыми и косвенными
тарифами).

S_1,2=
С_1,2—
(U₁
+ V₂)
= 5

S_1,3=
С_1,3—
(U₁
+ V₃)
= 12

S_1,4=
С_1,4—
(U₁
+ V₄)
= 3

S_1,5=
С_1,5—
(U₁
+ V₅)
= 7

S_2,1=
С_2,1—
(U₂
+ V₁)
= 3

S_2,3=
С_2,3—
(U₂
+ V₃)
= 6

S_2,4=
С_2,4—
(U₂
+ V₄)
= 3

S_2,6=
С_2,6—
(U₂
+ V₆)
= 0

S_3,1=
С_3,1—
(U₃
+ V₁)
= 1

S_3,2=
С_3,2—
(U₃
+ V₂)
= 4

S_3,3=
С_3,3—
(U₃
+ V₃)
= 3

S_3,5=
С_3,5—
(U₃
+ V₅)
= 5

S_4,2=
С_4,2
— (U₄
+ V₂)
= 6

S_4,4=
С_4,4—
(U₄
+ V₄)
= 7

S_4,6=
С_4,6—
(U₄
+ V₆)
= 2

Так как все оценки
S_i,j≥
0, то полученный
план является оптимальным, минимальные
транспортные расходы равны 285.

ЗАДАЧА
№ 2

Имеется заявка
на перевозку груза с условиями.
Необходимо доставить груз нескольким
потребителям, в рассматриваемом
примере равные эксплуатационные
условия в районе перевозки груза,
тогда в качестве критерия решения
задачи допустимо принять расстояние
перевозки груза, что будет соответствовать
минимальной стоимости для потребителя.

Потребность в
грузе первого пункта n₃—
2т.;

второго пункта
n₈-1т.;

третьего пункта
n₁₀—
5т.

Известны адреса
клиентов, поставщика и их взаимное
расположение; условия эксплуатации
– город. Взаимное расположение
поставщика и потребителей, расстояние
между пунктами представлены на рис.
6.

Число перестановок
из w
пунктов завоза (вывоза), включаемых в
маршрут по w
пунктам:

Pw
= w!,
(11)

где w!
– факториал целого положительного
числа w,
который равен произведению: w!
= 1·2·3…· w.
При трех пунктах груза количество
возможных маршрутов М
= w!
= 3! = 1·2·3 = 6, таким образом, возможны
шесть маршрутов доставки груза из
пункта В.
Выбор
маршрута осуществляется по критерию
«минимум затрат», чему соответствует
минимум пробега. При наличии двух и
более маршрутов одинаковой протяженности
цели системы соответствует минимум
грузооборота на маршруте. Результаты
расчета пробега и грузооборота
представлены в табл. 12.

Схема транспортной
сети, взаимное расположение пунктов,
длинны звеньев, потребность грузов в
развозочной системе представлены на
рис. 6.

n₈-q₂
= 1т

159 км

67 км

n₃—
q₁=
2т

134 км

81
км

190
км

n₁₀—
q₃
= 5т

Рис. 6 . Схема транспортной сети, взаимное
расположение пунктов, длинны звеньев,
потребность грузов в развозочной
системе

Таблица 12
Результаты расчета пробега и грузооборота в развозочной системе
Номер маршрута	Маршрут	Пробег, км.	Грузооборот, т·км
1	В-8-3-10-В	416	2599
2	В-10-3-8-В	430	1377
3	В-3-10-8-В	472	2360
4	В-3-8-10-В	441	2766
5	В-10-8-3-В	388	1410
6	В-8-10-3-В	405	1952

Вычислим
транспортную работу:

Р₁=
67∙8 + 159∙7 + 190∙5 = 2599 т·км;

Р₂=
81∙8 + 190∙3 + 159∙1 = 1377 т·км;

Р₃=
134∙8 + 190∙6 + 148∙1 = 2360 т·км;

Р₄=
134∙8 + 159∙6 + 148∙5 = 2766 т·км;

Р₅=
81∙8 + 148∙3 + 159∙2 = 1410 т·км;

Р₆=
67∙8 + 148∙7 + 190∙2 = 1952 т·км.

Примем для
дальнейшего проектирования системы
маршрут №5 –В-10-8-3-В, поскольку ему
соответствует минимальный пробег и
грузооборот. Расчет результатов
функционирования автомобиля в системе
выполним, используя модель развозочной
системы. Результаты представлены в
табл. 13.

Таблица 13
Результаты функционирования автомобиля в системе
Маршрут	Q, т	Le, км	P, т·км
В-10-8-3-В	8	388	1410

ВЫВОД

При
выполнении курсового проекта были
решены следующие вопросы и задачи:

Роль математических
методов в принятии эффективных
управленческих решений при автомобильных
перевозках. Виды моделей и эвристические
методы решения задач.
Понятие корреляционно-регрессионный
анализ.
Модели линейного программирования
в решении задач автомобильных перевозок
– основные понятия, графоаналитический
и симплексный методы.
Маршрутизация перевозок помашинными
отправками – основные этапы решения
задач.
Методы определения кратчайших
расстояний перевозок.
Методы планирования перевозок по
сборно — развозочным маршрутам.
Понятие о теории массового обслуживания
в решении задач автомобильных
перевозок.
Найдены оптимальные грузопотоки,
построен план перевозок.
Составлен граф (схема) транспортной
сети участка, выполнено проектирование
развозочного маршрута.

БИБЛИОГРАФИЧЕСКИЙ
СПИСОК

Моделирование
транспортных процессов и систем:
учебно-методический комплекс /сост.:
В.А. Янчеленко, В.А. Алексеев, И.В.
Таневицкий. — СПб.: Изд-во CЗТУ.
Бобарыкин, В.А.
Математические методы решения
автотранспортных задач: учеб. пособие
/В.А. Бобарыкин. – Л.: СЗПИ, 1986.
Горев, А.Э.
Грузовые автомобильные перевозки:
учеб. пособие /А.Э. Горев, — М.: Академия,
2008.
Зотов, Л.Л. Основы
теории автотранспортных систем:
учеб.- метод. компл., /Л.Л. Зотов, А.А.
Черняков, В.А. Янчеленко – СПб.: Изд-во
СЗТУ, 2008.

Источник

БАЗОВЫЕ ПОНЯТИЯ И ПОДХОДЫ ТРАНСПОРТНОГО МОДЕЛИРОВАНИЯ

А.1 Классификация методов моделирования транспортных потоков

За все время развития теории транспортных потоков появилось множество способов математического описания процессов поведения как потоков в целом, так и отдельных автомобилей и их взаимодействия между собой и транспортной инфраструктурой. Многие методы получили широкое распространение на практике для моделирования поведения транспортных потоков с целью прогнозирования и оценки их параметров. Существующие методы моделирования используют различный математический аппарат, основываются на различных допущениях, имеют различную степень детализации и, соответственно, обладают различными способностями, недостатками и преимуществами.

Ключевым классификационным признаком является способ описания объекта моделирования. Объектом моделирования является транспортный поток, и с точки зрения способа его описания можно выделить модели формирования спроса (travel demand models) и модели непосредственно транспортных потоков (traffic flow models). Первый тип моделей дает только количественную характеристику — объем движения или уровень спроса с разделением по различным видам транспорта, а второй описывает взаимосвязи внутренних параметров потока и показателей работы участков УДС. Вторым основным классификационным признаком является тип транспорта и корреспонденций, с этой точки зрения разделение идет на модели пассажирских и грузовых корреспонденций, а также модели пешеходных потоков.

С точки зрения подхода к описанию процесса формирования людских и материальных потоков, модели формирования спроса можно разделить на агрегированные и дезагрегированные.

Агрегированная модель оценивает объем поездок исходя из обобщенных параметров каждого транспортного района, таких как количество жителей, структура населения, число мест приложения труда, уровень автомобилизации, транспортная подвижность населения, наличие и характеристики грузообразующих объектов и т.д.

Дезагрегированные модели или модели цепочек действий (activity-based models) предполагают, что транспортные потребности жителя определяются его необходимостью принимать участие в некоторой деятельности в различное время и в различных местах. Каждое домохозяйство или даже отдельный житель рассматривается, как единица способная принимать решения. Конкретное транспортное поведение определяется исходя из стремления минимизировать затраты и максимизировать выгоды от различной деятельности. В данном типе моделей применяется математический аппарат методов условной оптимизации и теории дискретного выбора.

Модели непосредственно транспортных потоков — это математические модели, такие как гидродинамические, кинетические, клеточные автоматы, следования за лидером и т.д. Сами по себе такие модели не применяются на практике в чистом виде, а используются в качестве математической основы в специальных программных комплексах.

Описание транспортного потока разделяется на:

— агрегированное (макро-), оперирующее общими параметрами (скорость, плотность, интенсивность);

— дезагрегированное (микро-), где учитываются закономерности движения отдельных автомобилей или их небольших групп.

По способу получения информации о транспортном потоке модели делятся на:

— аналитические модели, которые основаны на теоретических и эмпирических зависимостях между параметрами транспортного потока и транспортной инфраструктуры;

— имитационные модели, которые стремятся описать и воспроизвести во времени процессы движения транспортных потоков и их взаимодействия с транспортной инфраструктурой.

Таким образом, с рассмотренных позиций модели транспортных потоков делятся на:

— аналитические макромодели,

— аналитические микромодели,

— имитационные макромодели,

— имитационные микромодели.

Аналитические макромодели представляют собой статическое распределение потоков по сети исходя из зависимостей скорости и плотности потока, полученных на основе фундаментальной диаграммы. Такой тип используется также в классической 4-х шаговой процедуре и присутствует во всех программных пакетах для транспортного планирования (EMME, CUBE, VISUM и др.).

Аналитические микромодели — это более детальное описание зависимостей, основанное на теории транспортных потоков. Такой подход используется, как правило, в программных продуктах, предназначенных для анализа локальных объектов (перекрестков, участков магистралей, развязок, круговых пересечений), к ним относятся, например, SIDRA INTERSECTION, HCS, ARCADY и т.п.

Имитационные макромодели описывают динамику развития ситуации на участке транспортной сети в терминах потоков в целом или «пачек» автомобилей. Такой подход характерен для программных продуктов по оптимизации режимов светофорного регулирования (TRANSYT, SATURN, SYNCHRO и др.).

Имитационные микромодели воспроизводят динамику движения транспортных потоков учитывая поведение и условия движения каждого транспортного средства. Наиболее известные представители программного обеспечения, реализующие этот подход: VISSIM, AIMSUN, PARAMICS и пр.

В литературе все чаще встречается понятие мезомоделей, как особого подхода к моделированию транспортных потоков. Однако определение такого подхода весьма расплывчато и нет единого мнения в вопросе, какой именно математический аппарат соответствует этому подходу. Мезоскопические модели рассматривают единичные транспортные средства, но описывают их движение и взаимодействие на основании статистических, агрегированных зависимостей. Мезомодели также могут быть аналитическими и имитационными.

Важным признаком классификации является назначение математических моделей транспортных потоков. Назначение, с точки зрения практического применения и решения конкретных задач, появляется у моделей только в составе специальных программных комплексов. Таким образом, классифицировать по назначению представляется возможным только готовое программное обеспечение для моделирования транспортных потоков. С этой позиции программные продукты делятся на применяемые для:

— предварительного (скетч) планирования, в т.ч. досетевые методы;

— стратегического планирования (прогнозирования);

— тактического планирования и управления (макро- и мезомодели);

— планирования работы отдельных видов транспорта (грузовой, ТОП, такси и др.);

— детального анализа движения потоков (микро- и мезомоделирование);

— оптимизации параметров координированного светофорного регулирования, в т.ч. в АСУДД;

— расчета геометрических параметров и параметров регулирования на отдельных перекрестках;

— анализа движения пешеходных потоков;

— оценки уровня безопасности движения.

Стоит отметить, что в последнее время наблюдается тенденция объединения инструментов для решения нескольких задач в едином программном комплексе или взаимосвязанном семействе продуктов одного разработчика. Также появляется много программных модулей стыковки между распространенными продуктами различного назначения для упрощения процесса ввода и обмена данными. Таким образом, отнесение многих программных продуктов к одной из перечисленных категорий по назначению оказывается затруднительным.

Для практических задач наиболее подходящим является разделение на категории по двум классификационным признакам:

— на основе подходов моделирования (макро-, мезо-, микро-);

— по принципу моделирования (аналитический и имитационный).

При этом, мезоподход, ввиду неопределенности его границ, следует рассматривать как вспомогательный и рекомендовать к применению совместно с одним из других подходов или как альтернативу при отдельном обосновании.

В таблице А.1 приведены сводные данные о классификации моделей транспортных потоков.

Таблица А.1

Результирующая классификация моделей транспортных потоков

Подход моделирования	Класс точности	Функциональность и назначение	Производительность	Примеры ПО
Макроаналитический	низкий	Прогноз перераспределения потоков на крупных сетях. Модели стратегического планирования и тактические модели.	очень высокая	EMME, TransCAD, VISUM, AIMSUN (v8), CUBE
Макроимитационный	средний	Прогноз перераспределения потоков с учетом фактора времени. Приближенная оценка показателей качества работы УДС. Задействование в контуре оптимизации параметров регулирования.	высокая	TRANSYT, SATURN, SYNCHRO, LinSig
Микроаналитический	высокий	Анализ показателей работы отдельных перекрестков, небольших участков магистралей.	высокая	SIDRA INTERSECTION, HCS, ARCADY
Микроимитационный	очень высокий	Детальный анализ показателей работы отдельных перекрестков, магистралей, небольших и средних сетей.	низкая	VISSIM, AIMSUN, PARAMICS, CORSIM
Мезоаналитический	средний	Анализ показателей работы отдельных перекрестков, магистралей, небольших, средних и крупных сетей.	очень высокая	н./д
Мезоимитационный	высокий	Анализ показателей работы отдельных перекрестков, магистралей, небольших, средних и крупных сетей.	средняя	AIMSUN, CONTRAM, DYNAMIT-P VISSIM (v8)

Также в задачах проектирования ОДД часто возникает необходимость моделирования пешеходных потоков. Описание динамики поведения пешеходов — это отдельное направление, основанное на принципиально иных закономерностях. В отличие от транспортных потоков у пешеходов нет полос движения, четких правил поведения, меньшие физические габариты, в плотных потоках допускается физический контакт и т.д. Среди моделей пешеходных потоков также встречаются макро- и микроуровни, применяются аналитические и имитационные подходы. Наиболее известными являются:

— модель магнетических сил (Magnetic Force Model);

— модель социальных сил (Social Force Model);

— клеточные модели (Benefit Cost Cellular Model) и др.

Среди программных продуктов можно выделить Legion, Myriad II, Mass Motion, блок пешеходного моделирования VISWALK в составе VISSIM и др.

Наиболее подходящей и наиболее адекватно и точно описывающей поведение пешеходов моделью в настоящее время является модель социальных сил. Рекомендуется использовать программные продукты на основе данного типа моделей в практике разработки проектов ОДД.

В современных условиях актуальным является также вопрос моделирования велосипедных потоков, особенно в условиях смешанного движения с автомобилями и пешеходами. Анализ современных публикаций показал, что для моделирования велосипедных потоков многими авторами предпринимались попытки адаптировать как модели, используемые для моделирования движения автомобилей (следования за лидером, клеточные автоматы), так и модели движения пешеходов (модели социальных сил). Ни один из подходов не дал удовлетворительных результатов по воспроизведению реального поведения велосипедистов. В литературе отмечается необходимость продолжения исследований в этом направлении и включения функционала моделирования велосипедных потоков в программные пакеты моделирования дорожного движения. Некоторые из современных программных продуктов позволяют моделировать велосипедное движение на основе тех же моделей, что и для автомобильных потоков, однако, как уже было отмечено, достоверность результатов такого моделирования не может быть гарантирована.

А.2 Основные принципы функционирования микромоделей транспортных потоков

К микромоделям транспортных потоков относятся модели, описывающие транспортный поток на уровне отдельных автомобилей или их небольших групп. Аналитическая микромодель представляет собой одну или несколько математических зависимостей, полученных в результате анализа эмпирических данных на основе различных подходов теории транспортных потоков или на основе теории систем массового обслуживания. Такая модель жестко связывает входные параметры с результатами расчета.

При имитационном моделировании динамические процессы системы-оригинала подменяются процессами, имитируемыми алгоритмом модели, с соблюдением тех же соотношений длительностей, логических и временных последовательностей, как и в реальной системе. Имитационное моделирование на микроуровне позволяет максимально точно оценить результирующие показатели качества работы сети, такие как уровень задержек, средняя скорость, число остановок, уровень загрузки и т.д.

На рисунке А.1 изображена обобщенная диаграмма процесса имитационного моделирования, который состоит из следующих этапов.

1. Формулирование проблемы и планирование операций: распознавание природы задачи, определение требований к отысканию ее решения.

2. Сбор данных и формирование модели: получение эмпирических свидетельств характеристиках поведения системы, выдвижение гипотез и преобразование их терминах соответствующего формального представления.

3. Контроль адекватности модели, т.е. проверка того, что ответы на вопросы типа «А что, если…», адресуемые модели, могут быть признаны верными.

4. Трансляция модели в форму компьютерной программы.

5. Проверка функционирования компьютерной программной модели.

6. Выработка проектных решений по преобразованию вопросов «А что, если…» в формат вычислительных экспериментов. Определение процедур выборки данных для целей статистического анализа и получения надлежащих ответов на вопросы.

7. Проведение имитационных компьютерных экспериментов и анализ результатов.

Основой имитационной микромодели дорожного движения является набор субмоделей описывающих определенные аспекты поведения водителей. К ним относятся: модель следования за лидером, модель смены полос, модель выбора безопасного промежутка в потоке, модель выбора скорости, модель слияния с потоком, модель обгонов.

Рисунок А.1 — Обобщенная диаграмма

процесса имитационного моделирования

Структуру имитационной микромодели можно представить через взаимодействие элементов системы ВАДС (водитель — автомобиль — дорога — среда).

Водитель. Данный элемент системы содержит вышеописанные модели поведения при движении в потоке (следования за лидером, смены полосы, выбора разрыва в потоке и т.д.), также учитывается присущее водителю время реакции, желаемая скорость движения, степень соблюдения ограничения скоростного режима и другие поведенческие характеристики.

Автомобиль. Элемент автомобиль описывается в основном физическими габаритами (длина и ширина), тягово-скоростными характеристиками, принадлежностью к какому-либо классу, пассажировместимостью и т.д.

Дорога. В рамках данного элемента системы описываются все параметры инфраструктуры, организации и управления движением. Сюда входят геометрические параметры УДС (число и ширина полос, радиусы поворотов, уклоны и т.д.), параметры ОДД (направления по полосам, запрет маневров, ограничение скорости, выделенные полосы и т.д.), параметры управления (режимы светофорного регулирования, параметры работы АСУДД и ИТС).

Среда. В понятие среды в имитационном моделировании входит воздействие на транспортные потоки погодных условий в части ограничения видимости и снижения сцепных качеств покрытия. Эти факторы приводят к снижению скорости движения и увеличению дистанции между автомобилями.

Таким образом, программные комплексы микромоделирования имитируют движение транспортных потоков на уровне взаимодействия элементов системы ВАДС. Это позволяет максимально точно оценить результирующие показатели качества работы участков дорожной сети.

В современных программных комплексах для микромоделирования транспортных потоков в стандартной комплектации, как правило, имеется возможность выбора нескольких разновидностей моделей, а также возможность загрузки пользователем любой другой модели.

В процессе имитации функционирования исследуемой системы, как при эксперименте с самим оригиналом, фиксируются определенные события и состояния, по которым вычисляются затем необходимые характеристики качества функционирования изучаемой системы (уровень задержек, средняя скорость, число остановок, уровень загрузки и т.д.). Каждый эксперимент с моделью имеет в основе некоторое случайное число, определяющее дальнейшее развитие событий в модели. Статистически достоверные результаты могут быть получены только путем усреднения результатов по нескольким репликациям (прогонам) модели. Число прогонов определяется в соответствии с положениями теории планирования эксперимента.

Используемые в программных комплексах микромоделирования субмодели имеют ряд параметров, которые могут быть изменены для более точного воспроизведения местных особенностей движения потоков в процессе калибровки модели. Число таких параметров в программных комплексах достигает нескольких десятков, и каждый из них оказывает определенное влияние на результат моделирования. Выбор того или иного значения каждого параметра требует наличия глубокого понимания теоретической и математической базы используемого программного продукта. В этой связи метод имитационного микромоделирования, а в особенности этап калибровки модели, предъявляет наивысшие требования к уровню квалификации специалистов.

А.3 Основные принципы функционирования моделей транспортного спроса и макромоделей транспортных потоков

Сферой использования макромоделей, в основном, является стратегическое и тактическое планирование развития транспортной системы и оценка масштабных проектов по ОДД, оказывающих влияние на движение транспортных потоков на значительной территории. Ключевая задача моделирования на таком уровне — расчет изменений спроса по видам транспорта, по времени совершения поездки и по маршрутам движения. Для первоначальной оценки спроса используются модели формирования транспортного спроса. На основе функционального анализа территории, социально-экономических данных и поведенческих характеристик населения такие модели позволяют оценить параметры транспортного спроса и представить его в виде матриц корреспонденций с разбивкой по целям поездок, категории пользователей и времени совершения поездок. Процесс расчета транспортного спроса и результирующих потоков по сети исторически сложился в последовательность действий, получившую название «классическая четырехшаговая процедура (модель)» (рисунок А.2). Основой построения модели является деление территории моделирования на транспортные районы, гомогенные с точки зрения функциональной роли и транспортной доступности. Второй, не менее важной составляющей, является модель транспортного предложения — набор графов имеющихся транспортных и маршрутных сетей со всеми присущими им атрибутами (длина, пропускная способность, разрешенная скорость, наличие регулирования, остановочных пунктов, парковки и т.д.).

Рисунок А.2 — Структура классической

четырехшаговой транспортной модели

Модель транспортного предложения дает представление о возможностях существующей транспортной инфраструктуры исследуемой территории с требуемой степенью точности. При этом требования к степени детализации данных о транспортном предложении определяются собственно объектом моделирования и конкретным кругом задач, для решения которых строится транспортная модель.

На выходе модель транспортного предложения формирует первичные матрицы затрат — таблицы, содержащие обобщенные оценки временных, денежных затрат и прочих затрат на перемещение между каждой парой транспортных районов в свободных условиях.

На этапе генерации поездок (Шаг 1) производится оценка суммарных объемов прибытия и отправления в каждом транспортном районе. Оценка объемов прибытия и отправления производится отдельно по каждой цели (слою) передвижений на основе следующих данных:

— данные о пространственном размещении населения и других объектов создания и притяжения передвижений, относящихся к определенной цели;

— данные о подвижности населения, то есть среднее количество поездок с данной целью, совершаемых в течение суток.

Для оценки объемов прибытия и отправления могут использоваться различные методы, такие как:

— регрессионные модели;

— перекрестная классификация;

— модели дискретного выбора.

На выходе первого шага получаются заготовки матриц корреспонденций, у которых правый столбец и нижняя строка заполнены значениями суммарного числа отправлений и прибытия по каждому району.

На этапе распределения поездок по зонам (Шаг 2) происходит расчет значений во всех остальных ячейках матрицы корреспонденций, т.е. числа поездок между каждой парой районов отправления/прибытия. С математической точки зрения задача распределения общего числа генерируемых в каждом районе поездок по остальным районам с соблюдением баланса суммарных значений отправления и прибытия имеет бесконечное число решений. Для получения результатов, которые отражают реальную ситуацию необходимо учитывать данные обследований транспортного поведения и фактических потоков, а также использовать специальные методы расчета. Наиболее адекватные результаты расчета межрайонных корреспонденций дает так называемая гравитационная модель: корреспонденция из одного района в другой будет тем больше, чем больше емкости районов прибытия и отправления, и чем ближе друг к другу расположены эти районы. При этом близость или дальность районов понимается не в географическом, а в транспортном смысле, в виде некоторой комплексной оценки быстроты и удобства передвижения по транспортной сети. Значения дальности или стоимости сообщения между каждой парой районов отправления/прибытия берутся из матрицы затрат, полученной в результате анализа модели транспортного предложения.

Еще одним распространенным методом расчета межрайонных корреспонденций является энтропийная модель, которая представляется в форме нелинейной оптимизационной задачи математического программирования. Качество результатов расчета с помощью энтропийной модели напрямую зависит от точности и полноты задания априорных условий по предпочтениям пользователей в перемещениях.

Этап расчета матриц корреспонденций является наиболее важным с точки зрения достоверности конечных результатов моделирования. Несмотря на то, что современные программные комплексы, как правило, имеют удобные встроенные средства расчета матриц корреспонденций, для их правильного использования необходимо иметь понимание теоретических положений, которые изложены в специальной литературе.

Таким образом, на выходе шага 2 должны быть получены матрицы корреспонденций для каждого слоя передвижений с разбивкой по времени суток при необходимости.

На этапе разделения поездок по видам транспорта (Шаг 3) происходит оценка того, какие виды транспорта (способы поездки) будут использоваться для реализации полученных на предыдущем шаге межрайонных корреспонденций. На выбор способа совершения поездки влияют как объективные параметры самой поездки, так и субъективные ощущения конкретного пользователя. Факторы, влияющие на выбор пользователем способа поездки, делятся на 3 группы:

— характеристики данного вида транспорта (в первую очередь скорость сообщения, надежность выполнения графика движения, дальность пешеходных подходов, продолжительность ожидания, связанного с необходимостью пересадки, стоимость поездки, а также уровень комфорта, безопасность, возможность телефонных разговоров во время поездки, доступ к Internet и т.п.);

— социально-экономический статус пользователя (наличие личного автомобиля, уровень дохода, состав семьи, деловые или социальные задачи, требующие автомобиля до, после или в рабочее время и т.п.);

— характеристики поездки (цель поездки, время ее выполнения, наличие стоянки и ее стоимость в пункте назначения, наличие попутчиков и их количество и т.п.).

Распределение межрайонных корреспонденций по доступным видам транспорта осуществляется на основе эмпирически полученных зависимостей или с помощью моделей, основанных на вероятностном дискретном выборе. В качестве критерия выбора используется максимизация полезности для пользователя или минимизация его затрат.

На выходе шага 3 получаются матрицы межрайонных корреспонденций для каждого способа передвижения.

На этапе распределения поездок по маршрутам (Шаг 4) оценивается нагрузка на транспортную сеть. Корреспонденции, которые по расчетам будут реализованы на индивидуальном автомобильном транспорте распределяются по возможным маршрутам следования. Наиболее распространенный в мировой практике подход к моделированию распределения потоков в транспортной сети основан на концепции «равновесного распределения потоков», сформулированной в 1952 г. профессором Уордропом. Равновесное распределение — это распределение автомобильных потоков по различным альтернативным путям в сети, возникающее в результате стремления всех участников движения уменьшить обобщенную цену своей поездки в сети с ограниченной пропускной способностью. В результате выбора всеми участниками движения (на основании предшествующего опыта) оптимальных путей, возникает распределение, в котором уже ни один участник не может так изменить свой путь, чтобы уменьшить его обобщенную цену (время движения). Время поездки по каждому маршруту определяется на основе макромодели транспортного потока, реализованной в виде функции отражающей зависимость времени проезда по участку от нагрузки на этот участок (CR или VDF функции).

Аналогично проводятся расчеты объемов и маршрутов движения грузовых корреспонденций. Маршрутные транспортные средства не участвуют в распределении и принимаются как фоновые потоки.

В результате расчета распределения поездок по маршрутам появляются новые значения времени проезда между транспортными районами, что может существенно повлиять на распределение поездок по районам. Для учета возможных изменений необходимо провести несколько итераций расчета начиная со второго шага описанной процедуры.

Приведенная последовательность расчета является наиболее общим случаем решения задачи определения транспортного спроса и нагрузки на УДС. Конкретные программные продукты могут иметь свои дополнения и особенности проведения таких расчетов. Дополнительную информацию и более подробное описание можно найти в специальной литературе.

А.4 Основные принципы оптимизации параметров светофорного регулирования

В процессе развития технологий расчета параметров светофорного регулирования сформировалось два основных подхода: расчетный и оптимизационный.

Расчетный метод основывается на эмпирических формулах, позволяющих оценить параметры регулирования, при которых будут обеспечены наилучшие условия движения. Такие формулы были выведены по результатам различных исследований. Наибольшее распространение получили модели, учитывающие как детерминированные, так и вероятностные свойства транспортного потока. Наиболее известной является формула Вебстера, она широко используется на практике по всему миру, но имеет свои ограничения. Одна из формул расчета задержки, наиболее точно учитывающих условия движения на регулируемом перекрестке, была представлена в американском руководстве по пропускной способности дорог (HCM 1994 — Highway Capacity Manual). Сравнительное тестирование аналитических моделей HCM 2000, CCG 1995 и формулы Вебстера, показало, что в условиях малонасыщенного потока оценки задержек имеют приблизительно одинаковые результаты. Вместе с тем, оценки задержек по методике HCM 1994 занижены, особенно это проявляется при уровне насыщения подхода v/c > 1. Формула Вебстера при уровне загрузки v/c > 1 теряет смысл, работоспособными остаются модели HCM 2010, HCM 1994 и CCG 1995.

При выводе формул для определения показателей уровня обслуживания на перекрестке допускались гипотезы, упрощающие аналитические выводы, но ослабляющие практическую применимость моделей. Таким образом, используемые в настоящее время аналитические алгоритмы и модели не всегда выдают адекватную оценку задержек транспортных средств на регулируемых перекрестках. В условиях транспортных потоков высокой плотности расчеты по различным формулам приводят к совершенно различным результатам. Кроме того, аналитические формулы применимы только для отдельных перекрестков и не позволяют рассчитать параметры координированного управления.

Второй подход заключается в поиске наилучших параметров регулирования при помощи алгоритмов оптимизации, при этом оценка параметров производится с использованием некоторой модели. Результаты, полученные оптимизационным методом, во многом зависят от качества модели, используемой в контуре оптимизации.

В качестве критерия оптимизации может выступать минимизация суммарной задержки транспортных средств, выравнивание загрузок транспортных направлений, минимизация задержек всех участников движения, минимизация объема эмиссии выхлопных газов и др.

Наиболее распространенным методом оптимизационного расчета параметров светофорного регулирования является алгоритм TRANSYT (TRAffic Network StudY Tool), разработанный TRL (Великобритания) в начале 70-х годов и продолжающий совершенствоваться до настоящего времени. В рамках метода реализуется итерационный процесс взаимодействия двух основных структурных блоков: имитационной модели и оптимизатора. Имитационная модель позволяет на основании сведений о текущих значениях параметров регулирования, информации о транспортных потоках и временах проезда между стоп-линиями рассчитать значение критерия оптимальности. Оптимизатор изменяет значения параметров регулирования, анализируя полученное значение критерия оптимальности и реализуя заданную пользователем стратегию. Стратегия поиска наилучших параметров регулирования в TRANSYT представляет собой сочетание метода случайного поиска с градиентным спуском, а также использует генетический алгоритм в одной из последних версий.

Таким образом, в процессе разработки проектов АСУДД в городских условиях, где основным средством воздействия на транспортный поток являются светофорные объекты, моделирование может использоваться при расчете параметров регулирования в рамках метода TRANSYT и ему подобных. Для детальной оценки результатов расчета следует использовать имитационное микромоделирование. Для оценки работы магистральных АСУДД наилучшим инструментом также является микромоделирование.

Приложение Б

Скачать документ целиком в формате PDF

Источник

Душевская А.В. 1, Лапина Л.А. 1

1Сибирский Федеральный Университет

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Анализ бизнес-процессов сегодня распространен очень широко и проводится в каждой организации, желающей повысить эффективность своей работы. Грамотно произведенные оптимизация или реинжиниринг бизнес-процессов помогают решать организациям всевозможные актуальные для них проблемы.

Организации могут вынести для себя большую выгоду, располагая в наличии документированной моделью бизнес-процессов. Это придает ее деятельности большую прозрачность, что в свою очередь является дополнительным стимулирующим фактором инвестиционной привлекательности для организации.

Для развивающихся компаний, стремящихся обеспечить конкуренцию на рынке, особенно важно четкое понимание роли моделирования бизнес-процессов и его необходимости, и места в организации.

Одним из главных факторов успеха деятельности транспортной компании становится совершенствование существующего бизнес процесса, связанного также с перевозочным процессом.

Чтобы бизнес процесс соответствовал всем требованиям, а также был понятен каждому сотруднику, его нужно исчерпывающе описать. Есть несколько методов описания бизнес процессов:

собственно моделирование бизнес процесса – для него используют стандарт IDEF0, с помощью которого можно описать весь процесс от низшего до высшего уровня в его функциональном процессе;
описание потока работ – этот метод близок к алгоритмическому, для описания которого пользуются стандартом IDEF3;
метод описания потока данных – с его помощью описываются последовательности работ с помощью DFD;
некоторые другие методологии.

В данной работе рассмотрены основные методы моделирования бизнес-процессов транспортных компаний, приведены их достоинства и недостатки.

Для моделирования информационных систем используется несколько различных методов, основой которых являются как структурный, так и объектно-ориентированный подходы к моделированию. Ниже рассмотрены основные методы моделирования.

Моделирование потоков данных DFD

В основе данного метода лежит построение модели информационной системы предприятия. В соответствии с методом модель системы определяется как иерархия диаграмм потоков данных (DFD), описывающих функциональные процессы преобразования информации. Диаграммы верхних уровней иерархии определяют основные процессы (подсистемы) с внешними входами и выходами. Они детализируются при помощи диаграмм нижнего уровня. Цель такого представления – продемонстрировать, как каждый процесс преобразует свои входные данные в выходные, а также выявить отношения между этими процессами. Метод DFD используются для описания процессов при внедрении процессного подхода к управлению организацией. Нотация DFD позволяет описывать потоки документов (документооборот) и потоки ресурсов (например, движение материалов от одной работы к другой).

Метод функционального моделирования SADT (IDEF0)

Метод SADT (Structured Analysis and Design Technique) представляет собой совокупность правил и процедур, предназначенных для построения функциональной модели информационной системы предприятия. Основой метода является структурирование деятельности организации в соответствии с ее процессами. Построенная функциональная модель информационной системы содержит диаграммы, фрагменты текстов и глоссарий. Основные преимуществами метода являются полнота описания предметной области, возможность детализации потоков данных и информации, получение моделей стандартного вида и простота документирования процессов.

Методология моделирования IDEF3

Модель в нотации IDEF0 позволяет получить общее представление о функциях, выполняемых моделируемой системой, и связях между функциями, действиями. Модель в нотации IDEF3 позволяет проследить логику взаимодействия процессов, функций. Техника IDEF3 является частью структурного анализа. Можно сначала построить функциональную модель в нотации IDEF0, проведя исследования предметной области. Затем, используя полученные знания о предметной области, построить отдельную модель в нотации IDEF3. А можно создать смешанную модель, дополняя по мере необходимости функциональную модель в нотации IDEF0 диаграммами в нотации IDEF3. Также можно дополнять модель DFD диаграммами в нотации IDEF3.

В данной работе проведено сравнение наиболее популярных методов, предназначенных для моделирования бизнес-процессов транспортных компаний. Каждый метод имеет свои достоинства и недостатки, поэтому говорить о преимуществе той или иной методологии бессмысленно. В зависимости от целей моделирования и масштаба предметной области эти преимущества могут, как усиливаться, так и ослабевать.

Источник

Библиографическое описание:

Майоров, Н. Н. Факторы выбора имитационного моделирования, как универсального средства, для исследования транспортных процессов / Н. Н. Майоров. — Текст : непосредственный // Проблемы и перспективы экономики и управления : материалы I Междунар. науч. конф. (г. Санкт-Петербург, апрель 2012 г.). — Санкт-Петербург : Реноме, 2012. — С. 224-228. — URL: https://moluch.ru/conf/econ/archive/15/2086/ (дата обращения: 23.03.2023).

В
настоящее время моделирование является основным методом исследований
во всех областях знаний и научно обоснованным методом оценок
характеристик сложных систем, в частности транспортных, используемым
для принятия решений в различных сферах деятельности. При выполнении
моделирования решается задача определения структуры процесса. При
проектировании сложных транспортных систем и их подсистем возникают
многочисленные задачи, требующие оценки количественных характеристик
и качественных закономерностей процессов функционирования таких
систем. Ограниченность возможностей экспериментального исследования
больших транспортных систем делает невозможным их полное
проектирование, внедрение и эксплуатацию без использования методики
моделирования, которая позволяет в соответствующей форме представить
процессы функционирования систем и описание протекания этих процессов
с помощью математических моделей. Наибольшее распространение при этом
получили аналитический и имитационный методы моделирования. При
аналитическом исследовании транспортных систем полное исследование
удается провести в том случае, когда получены явные зависимости,
связывающие искомые величины с параметрами системы и начальными
условиями ее изучения. Однако это удается выполнить только для
сравнительно простых транспортных систем. Анализ характеристик
процессов функционирования сложных систем с помощью только
аналитических методов наталкивается на значительные трудности,
приводящие к необходимости существенного упрощения моделей и
получению недостоверных результатов. Поэтому чаще всего для
исследования транспортных систем используют имитационные модели.

Математический
аппарат, применяемый в имитационном моделировании практически нечем
неограничен [2]. В основе данного моделирования транспортных систем,
лежит моделирование случайных явлений. Благодаря наличию возможности
производить различную генерацию событий существует реальная
возможность прогнозировать различные события в транспортной системе.
Рассмотрим сферу применения имитационных моделей (рис. 1).

Рис.
1.
Транспортные
задачи

Рассмотрим каждый процесс в
отдельности и обоснуем правильность использования имитационного
моделирования для их решения.

1.
Планирование и составление расписаний
работы транспортной системы. Практически
любая производственная или логистическая деятельность требует
составления расписания чего-либо в том или ином виде. Часто данная
задача может быть довольно просто решена, например, если нет никакой
вероятностей, и парк, например, автомобилей составляет 5 единиц, то
эффективное расписание можно составить исходя из простых логических
умозаключений. Но если есть производство, сложный технологический
процесс, значительный парк транспортных средств, то составить
эффективное расписание «вручную» может быть сложно, если
вообще возможно. В общем виде, составление расписания или любое
планирование во времени взаимосвязанных динамических событий является
сложной и, как правило, не решаемой аналитически задачей.
Единственным методом, который позволяет найти оптимальное расписание
в общем случае, является полный перебор всех возможных вариантов
развития событий, но решить подобную систему невозможно, т.к. события
развиваются во времени, и чем дальше мы смотрим вперед, тем больше
различных вариантов получаем, и количество необходимых расчетов
растет в геометрической прогрессии. Поэтому для составления сложных
расписаний используется комбинация имитационных моделей со
специальными оптимизационными эвристиками, которая позволяет найти
расписание, близкое к оптимальному.

2.
Управление парком транспортных
средств и перевозками содержит
следующие задачи: стратегическое и оперативное управление парком
транспортных средств; оптимизация
и планирование перевозок; автоматизация
бизнес-процесса по управлению перевозками, в том числе и процесса
принятия управленческих решений; минимизация
затрат на управление перевозками и содержание парка;
оценка
рисков принимаемых решений. Управление парком и перевозками включает
в себя множество различных аспектов, например, комплектование парка,
закупку новых транспортных средств, план регламентных работ,
управление человеческими ресурсами, так же, как и непосредственное
управление перевозками, т.е. какое транспортное средство, когда и
куда надо направить. Управление перевозками является наиболее сложной
задачей среди перечисленных и фактически сводится к долгосрочному и
краткосрочному планированию, в частности, составлению расписания
перевозок, а также оперативному управлению транспортными средствами.
Требования к управлению могут выдвигаться совершенно разные,
например, максимизация объема перевозок, минимизация стоимости
перевозок, или вероятность выхода стоимости перевозок за рамки
бюджета. Однако, независимо от требований, аналитического решения для
задачи составления расписания не существует, и единственным способом
решения являются системы поддержки принятия решений на основе
оптимизирующих имитационных моделей, которые позволяют получить
результат близкий к оптимальному. Такие модели позволяют «проиграть»
различные схемы управления парком с учетом текущей дислокации,
проанализировать различные варианты развития событий и выбрать
наиболее эффективное решение на данный момент времени.

3.
Управление транспортными сетями.
Транспортные сети (дате ТС) объединяют в себя все ресурсы и процессы,
необходимые для хранения и доставки грузов: транспортные средства,
маршруты доставки, склады и терминалы, фронты погрузки/разгрузки,
информационные системы. Управление транспортной сетью в целом стоит
на уровень выше, чем управление парком транспортных средств или,
например, терминалом. Фактически, управление ТС дает общий взгляд на
всю транспортную систему в целом, а задача эффективного управления ТС
фактически сводится к эффективному управлению всеми ее ресурсами и
процессами. Таким образом, возможность учитывать особенности всех
узлов системы в их взаимосвязи позволяет снизить затраты и сократить
риски при принятии управленческих решений и рисками потенциальных
финансовых потерь.

4.
Управление цепочками поставок. Цель
управления цепочками поставок состоит в объединении рынка сбыта,
системы распределения, производства и закупки таким образом, чтобы
клиенты обслуживались на более высоком уровне при одновременном
снижении затрат. Управления цепочками поставок состоит из трех
основных этапов:

принятие
решений (время и состав закупок, точка заказа и уровень заказа, пути
доставки, какие складские площади и когда надо освободить и т.д.);
мониторинг
состояния заказов ;
документирование
процесса.

Наиболее
сложным этапом, является процесс принятия решений, так как необходимо
проанализировать множество взаимосвязанных, часто стохастических
событий. Тем не менее, большинство систем по управлению цепочками
поставок предоставляет только возможности мониторинга и
документирования процесса, что является необходимой составляющей, но
все же не основной. Имитационные модели позволяют полностью
спрогнозировать процесс управления цепочками поставок от принятия
решений до мониторинга их выполнения и документирования.

5.
Склады и терминалы. Склад
является неотъемлемой частью любой цепочки поставок – все
начинается со склада, складом же все и заканчивается. Без учета
параметров склада, его ресурсов, динамики движения товаров невозможно
эффективно управлять цепочкой поставок в целом. От того, насколько
эффективно работает склад, как используются его площади и ресурсы, в
значительной степени зависит результативность функционирования всей
логистической структуры. Например, нередко приходится сталкиваться с
ситуациями, когда из-за неэффективной работы склада или терминала
вагоны могут более суток ожидать погрузки, в то время как само время
перевозки составляет два-три дня, т.е. фактически эффективность
перевозок в таких случаях падает на 50%. Также одним из интересных
приложений имитационных моделирования является анализ сети терминалов
и складов. Имитационные модели помогают проанализировать различные
варианты расположения терминалов и складов, организовать грузопотоки,
оценить, как терминалы будут реагировать на увеличение грузопотока, в
какой очередности рекомендуется строить терминалы – и все это
делается с учетом реальных стохастических характеристик, а не средних
величин и непонятно как полученных коэффициентов, которые, как
правило, дают результаты, значительно отличающиеся от фактических.

Общий
процесс построения транспортной модели, осуществляемый при
имитационном моделировании транспортной системы, делится на следующие
этапы: постановка задачи, определение цели исследования в
транспортной системе, разработка системы в рамках принятых допущений;
планирование имитационного эксперимента на вычислительной станции;
испытание модели в соответствии с намеченным планом и получение
результатов для последующего формирования решения.

Рассмотрим транспортную
задачу и ее реализацию с помощью имитационной модели. За основу
возьмем морской логистический комплекс. При проектировании нового
порта или анализа работы уже существующего, часто возникает задача в
определении
числа причалов, необходимых для работы порта без перегрузки и
простоя. Решение данной задачи необходимо в целях оптимизации работы
всей морской транспортной системы. Структура данного процесса
приведена на рис 2.

Рис
2. Структура транспортных процессов и реализация транспортной модели

На
вход системы подается поток кораблей, которые ждут разгрузки возле
причалов или находятся на подходе к ним в акватории порта. Порт
содержит определенное число причалов, которые могут обработать суда.
При имитационном моделировании выполняется генерация различного числа
судов. Имитационное моделирование
движения судов в акватории порта реализовано в среде AnyLogic
версии 6.4.1 [1] (рис. 3).

Рис.
3.
Имитационная модель движения судов в акватории порта

В результате работы
имитационной модели получаются качественные, количественные и
графические характеристики работы блоков “поток кораблей”,
“рейд”, “причалы” указанные на
рис.2. Как видно на рис.3 задано три транспортных потока и причалы не
могут справиться с определенным входным потоком судов. Очередь из
судов, ожидающих разгрузки, увеличивается. Количественные
характеристики данного транспортного процесса являются основой для
расчета оптимального числа причалов, которые обеспечат оптимальную
работу портового комплекса. Результаты расчета и графические
характеристики приведены в таблице 1 и рис.4

Таблица
1

Число устройств (Причалы)	6	7	8	9	10	11	12
Среднее время ожидания (Рейд, Все типы заявок)	11,7	9,37	2,08	0,141	0,0183	0,00202	0,000155
Среднее время простоя (Причалы, Все типы заявок)	0,00153	0,00232	0,199	1,18	2,18	3,2	4,23

Рис.4 График зависимости
коэффициента загрузки и среднего ожидания судна на рейде

Таким
образом, проанализировав зависимости на рис. 4 и таблице 1, можно
прийти к выводу, что для эффективного функционирования морского порта
необходимо наличие 8 или 9 причалов. При таком количестве причалов
портовая система будет работать оптимально и удается минимизировать
простои судов и причалов.

Следующей
транспортной задачей, которую необходимо исследовать, является
моделирование работы каждого причала в отдельности. Данный
транспортный процесс также реализован с помощью имитационной модели
(рис 5).

Рис
5. Имитационная модель работы причала для контейнерных судов

В
результате проведенного исследования обоснованы факторы, при которых
использование имитационного моделирования для решения транспортных
задач является наиболее эффективным. Приведена классификация
транспортных задач. В завершении приводится системное решение
транспортной задачи в морском логистическом комплексе и итоговые
имитационные модели.

Литература:

Каталевский
Д.Ю. Основы имитационного моделирования и системного анализа в
управлении / Д.Ю. Каталевский – М.: МГУ, 2011, – 304 с.
Майоров
Н.Н., Фетисов В.А. Моделирование транспортных процессов / Н.Н.
Майоров, В.А.Фетисов – СПб. ГУАП, 2011, – 165 c.

Основные термины (генерируются автоматически): имитационное моделирование, транспортная система, задача, управление цепочками, имитационная модель, модель, принятие решений, причал, система, склад, транспортная задача, управление парком, управление перевозками, цепочка поставок.

Динамическое моделирование бизнес процессов в транспортных системах

Моделирование бизнес-процесса организации перевозок транспортно-логистической компанией

Введение

1.
Описание предметной области

2.
Моделирование проектируемой системы

.1
Диаграмма вариантов использования

2.2
Диаграмма классов

2.3
Диаграмма последовательности

2.5
Диаграмма состояний

Заключение

Список
литературы

Общее представление о моделировании транспортных процессов

Математическое моделирование транспортных процессов

Особенности моделирования транспортных процессов

Библиографическое описание:

Похожие статьи

Разработка и исследование мультиагентных моделей

Имитационное моделирование транспортно-пересадочных узлов

Моделирование развития региональной…

Использование имитационного моделирования в оценке…

Моделирование условий пропуска поездов в программном…

Компьютерное имитационное моделирование как способ…

Ключевые аспекты имитационного моделирования сложных…

Моделирование — инструмент апробации реальных систем

Применение математического моделирования при исследовании…

Моделирование бизнес-процесса организации перевозок транспортно-логистической компанией

Введение

1. Описание предметной области

2. Моделирование проектируемой системы

.1 Диаграмма вариантов использования

2.2 Диаграмма классов

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" height="197" src="https://www.bibliofond.ru/wimg/11/551249.files/image002.gif" />

2.3 Диаграмма последовательности

2.5 Диаграмма состояний

Заключение

Список литературы

Общее представление о моделировании транспортных процессов

Математическое моделирование транспортных процессов

Особенности моделирования транспортных процессов

Библиографическое описание:

Похожие статьи

Разработка и исследование мультиагентных моделей

Имитационное моделирование транспортно-пересадочных узлов

Моделирование развития региональной…

Использование имитационного моделирования в оценке…

Моделирование условий пропуска поездов в программном…

Компьютерное имитационное моделирование как способ…

Ключевые аспекты имитационного моделирования сложных…

Моделирование — инструмент апробации реальных систем

Применение математического моделирования при исследовании…

1.
Описание предметной области

2.
Моделирование проектируемой системы

.1
Диаграмма вариантов использования

2.2
Диаграмма классов

2.3
Диаграмма последовательности

2.5
Диаграмма состояний

Список
литературы