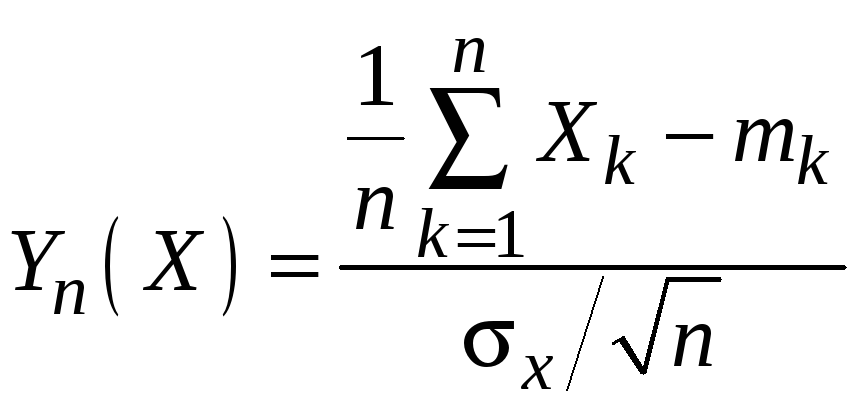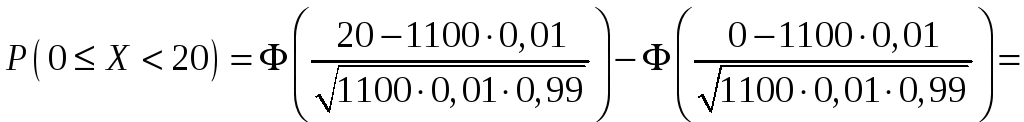Автомобиль должен проехать по улице на которой установлено 3 светофора дающие независимо

Номер задачи: Tv-11

Решение: бесплатно

Автомобиль должен проехать по улице, на которой установлено четыре независимо работающих светофора. Каждый светофор с интервалом в 2 мин подает красный и зеленый сигналы; СВ — число остановок автомобиля на этой улице.

Найти закон распределения указанной дискретной СВ и ее функцию распределения F(x). Вычислить математическое ожидание M(x) , дисперсию D(x) и среднее квадратичное отклонение σ(x). Построить график функции распределения.

Посмотреть другие задачи

Отправить также файл на почту

Заказать / Оценить подобную работу

Отправить также файл на почту

Источник

Автор
Тема: Мат ожидание, объясните пожалуйста. (Прочитано 2213 раз)

0 Пользователей и 1 Гость просматривают эту тему.

объясните пожалуйста решения, нужно писать работу по этой теме, а разбираюсь только в теории…

Автомобиль должен проехать по улице, на которой установлены три светофора, дающие независимо друг от друга зеленый сигнал в течение 1,5 мин, желтый 0.3мин и красный 1.2мин. Постройте ряд распределения случайной величины ξ — числа остановок автомобиля на этой улице. Найдите Мξ , Dξ , σ ξ , Р { ξ ≥ 2},Р { ξ = 0,5},Р {0 ≤ ξ < 2},Р { ξ < Мξ}. Постройте график функции Fξ(x). Какова размерность Мξ , Dξ ?

неужели никто не знает. объясните хотя бы частично.

Источник

0 / 0 / 0

Регистрация: 07.06.2013

Сообщений: 8

07.06.2013, 16:41. Показов 3095. Ответов 2

Автомобиль должен проехать 3 светофора, дающие, независимо друг от друга, зеленый сигнал в течение 1,5 мин, желтый — 0,3 мин, красный — 1.2 мин. Написать закон распределения остановок и построить график. Подскажите как избавиться от времени. Спасибо огромное

1943 / 1051 / 160

Регистрация: 06.12.2012

Сообщений: 4,604

08.06.2013, 02:16

Замените время на вероятности. Например для зелёного р=1,5/(1,5+0,3+1,2)

0 / 0 / 0

Регистрация: 07.06.2013

Сообщений: 8

09.06.2013, 11:53

[ТС]

Спасибо Вам большое

Источник

Предельные теоремы теории вероятностей

Теорема
Бернулли.
Относительная частота успехов в

независимых испытаниях по схеме Бернулли
сходятся по вероятности при

к вероятности успеха в одном испытании.

Центральная
предельная теорема (Ляпунова).
Если случайные
величины в последовательности

независимы, одинаково распределены и
имеют конечные математическое ожидание

и дисперсию
,
то для любого действительного

,
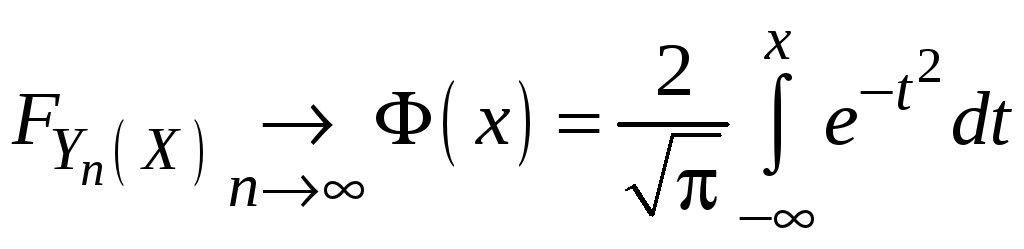
где

– стандартизированное среднее
арифметическое

случайных величин в последовательности.

Пусть

– число успехов в

независимых испытаниях по схеме Бернулли.
Тогда при достаточно больших значениях

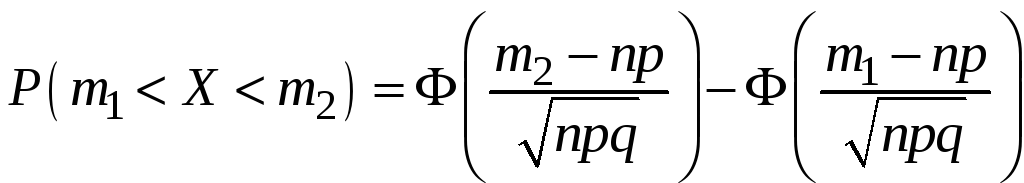
где

– табулирована и

(интегральная теорема
Муавра –
Лапласа).

,
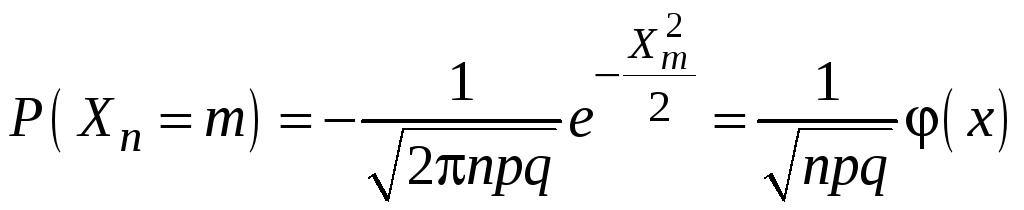
где ,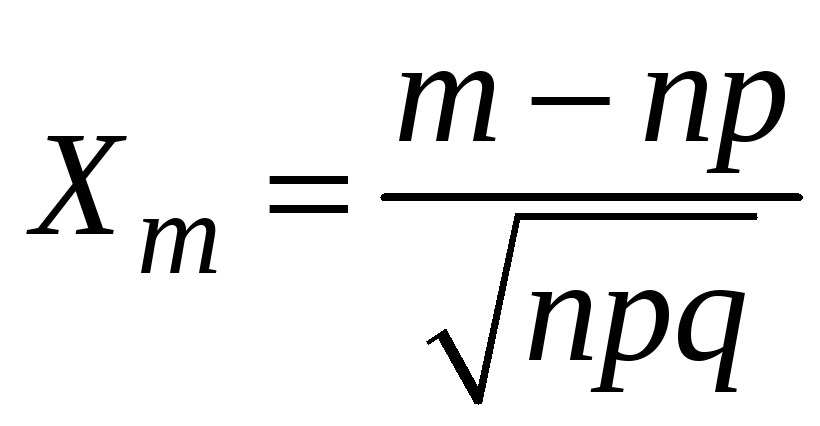

– функция
табулирована (локальная теорема Муавра
–
Лапласа).

Пример
1.

Вероятность
появления события в каждом из независимых
испытаний равна 0,8. Найти вероятность
того, что событие наступит 120 раз в 144
испытаниях.

Решение.

По
условию задачи
.
Воспользуемся локальной теоремой
Лапласа. Найдем значение аргумента

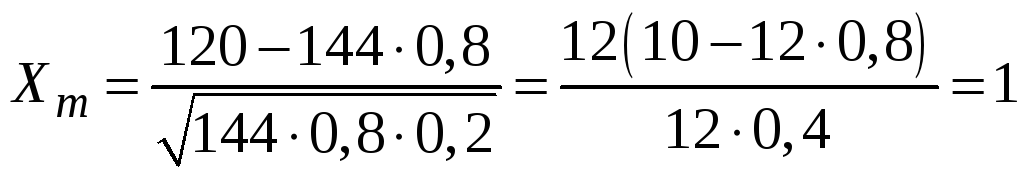
По
таблице функций

находим, что
.
Искомая вероятность равна

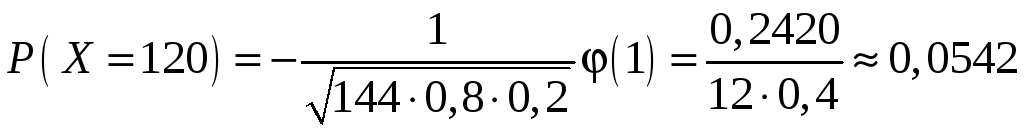
Пример 2.

Радиотелеграфная
станция передает цифровой текст. В силу
помех каждая цифра независимо от других
может быть неправильно принята с
вероятностью 0,01. Найти вероятность
следующих событий:
(в
принятом тексте, содержащем 1100 цифр,
будет меньше 20 ошибок),
(будет
сделано ровно 7 ошибок).

Решение.

Для
вычисления вероятности события

применим интегральную
теорему Муавра
– Лапласа.

.
Искомая
вероятность будет

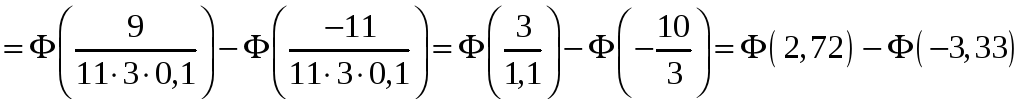
По
таблицам функции

находим, что

Искомая
вероятность равна

4.5. Варианты заданий для контрольной работы № 6 Задача 1

Случайная
величина

– число попаданий в корзину при одном
броске. Вероятность попадания равна
0,3. Найти
.
Случайная
величина

– число попаданий мячом в корзину при
двух бросках. Вероятность попадания
равна 0,4. Найти
.
Устройство
состоит из трёх независимо работающих
элементов. Вероятность отказа каждого
элемента в одном опыте равна 0,1. Случайная
величина

– число отказавших элементов в одном
опыте. Найти
.
Дискретная
случайная величина

– число мальчиков в семьях с четырьмя
детьми. Рождение мальчика и девочки
считаются равновероятными. Найти
вероятности событий:
,
,
.
Производится

опытов по схеме Бернулли. Вероятность
«успеха» в каждом опыте равна
.
Случайная величина

– число «неудач» в

– опытах. Построить график функции
распределения при
=5,
=0,5.
В
урне 5 белых и 25 чёрных шаров. Вынимается
один шар. Случайная величина

– число вынутых белых шаров. Найти
.
Автомобиль
должен проехать по улице, на которой
установлены три светофора, дающие
независимо друг от друга зелёный сигнал
в течение 1,5 мин., жёлтый – в течение
0,3 мин., красный – в течение 1,2 мин.
Случайная величина

– число остановок автомобиля на этой
улице. Найти
.
В
коробке имеется 7 карандашей, из которых
4 красные. Из коробки извлекают три
карандаша. Случайная величина

– число красных карандашей в выборке.
Найти вероятность события

и
.
На
пути движения автомобиля расположены
4 светофора. Каждый из них, с вероятностью
0,5 либо разрешает, либо запрещает
движение. Случайная величина

– число светофоров, встреченных машиной
до первой остановки. Найти
.
Имеются
5 ключей, из которых только один подходит
к замку. Случайная величина

– число проб при открывании замка;
испробованный ключ более не используют.
Найти
.
В
ящике лежат

– изделий, из которых одно бракованное.
Из ящика извлекают изделия одно за
другим до тех пор, пока не будет вынуто
бракованное изделие. Случайная величина

– число вынутых изделий. Найти
.
Выбирают
по одной букве из слов день и ночь.
Случайная величина

равна 1, если обе буквы гласные;
=0,
если буквы согласные;

в остальных случаях. Найти
.
Производится
два независимых выстрела по мишени.
Случайная величина

– разность между числом попаданий и
числом промахов. Вероятность попадания
при каждом выстреле равна
.
Найти
.
Дискретная
случайная величина

задана законом распределения

	-2	-1	0	1	2
	0,1	0,2	0,2	0,4	0,1

Найти
.
Найти вероятности событий:;
.

Дискретная
случайная величина

задана законом распределения

	0	1	2	3	4
	0,05	0,2	0,3	0,35	0,1

Найти
.
.

Дан
ряд распределения случайной величины

	10	20	30	40	50
	0,2	0,3	0,35	0,1	0,05

Найти
.

Случайная
величина

– число очков, выпавших на верхней
грани игральной кости при её бросании.
Определить тип случайной величины, и
найти её закон распределения.
Закон
распределения случайной величины

характеризуется следующей таблицей

	0	2	3	6
	0,2	0,3	0,1	0,4

Найти
аналитический вид функции распределения
случайной величины

и
построить график

Случайная
величина

принимает значения – 2, 0 и 2 с вероятностями,
соответственно, равными
.
Найти

и построить её график.
Случайная
величина

характеризуется следующим распределением
вероятностей

	–3	–2	0	1	3
	0,2	0,1	0,2	0,4	0,1

Найти

и построить график.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Kontrolnaya_rabota_po_matematike_4

Подставляя данные в формулу, получаем

p ( A ) = 0,72 0,99 + 0,18 0,95 + 0,08 0,9 + 0,02 0,8 ≈ 0,97.

Тогда вероятность отказа реле

2.16.–2.20. Изделие поступает для обработки на одну из трех линий производительностью 12, 4 и 9 изделий в час соответственно. Брак может возникнуть на любой из этих трех линий, причем наблюдения показали появление дефектов: на первой – 2% изделий, на второй – 3%, на

третьей – 4% изделий. Считая, что вероятность попадания изделия на

ту или иную линию пропорциональна ее производительности, определить: 1) вероятность того, что случайно выбранное изделие окажется бракованным; 2) вероятность того, что случайно выбранное бракованное изделие изготовлено на первой линии.

Пусть A −событие, состоящее в том, что случайно выбранное изделие является бракованным.

Всего в час выпускается 12 + 4 + 9 = 25 изделий.

Вычислим вероятности гипотез:

A/H k −событие, состоящее в том, что дефект

По условию задачи вероятности этих событий равны

По формуле полной вероятности найдем вероятность того, что выбранное изделие бракованное

Подставляя данные в формулу, получаем

Вероятность того, что случайно выбранное бракованное изделие изго-

товлено на первой линии, вычислим по формуле Байеса

2.21.–2.25. Предохранитель в электрической цепи отказывает при коротком замыкании в электронной лампе с вероятностью p 1 = 0,4, при

лее вероятную причину отказа предохранителя после того, как такое событие произошло.

Пусть A−событие, состоящее в том, что произошел отказ предохранителя. Данное событие наступит при осуществлении одной из гипотез: H 1 −событие, состоящее в том, что произошло короткое замыкание в

электронной лампе; H 2 −событие, состоящее в том, что произошло замыкание обмотки трансформатора; H 3 −событие, состоящее в том, что произошел пробой конденсатора; H 4 −событие, состоящее в том, что

произошли другие причины, вызывающие отказ предохранителя. По условию задачи вероятности этих гипотез до опыта равны:

Рассмотрим события: A/H 1 −событие, состоящее в том, что предохранитель отказал из-за короткого замыкания в электронной лампе; A/H 2 −

событие, состоящее в том, что предохранитель отказал из-за замыкания обмотки трансформатора; A/H 3 −событие, состоящее в том, что предо-

хранитель отказал из-за пробоя конденсатора; A/H 4 −событие, состоящее в том, что предохранитель отказал по другим причинам.

событий по условию задачи равны

мулу полной вероятности:

p ( A ) = p ( H 1 ) p ( A/H 1 ) + p

Подставляя данные в формулу, получаем

пользуя теорему Байеса: p ( H 1 ) p ( A/H 1 )

Источник

LiveInternetLiveInternet

—Ссылки

—Рубрики

—Метки

—Приложения

—Поиск по дневнику

—Подписка по e-mail

—Статистика

Решенные задачи по теории вероятностей (по вариантам) 2

Вариант 1
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)

1.1. Автомобиль должен проехать по улице, на которой установлено четыре независимо работающих светофора. Каждый светофор с интервалом в 2 мин подает красный и зеленый сигналы; СВ X – число остановок автомобиля на этой улице.

2. Дана функция распределения F(х) СВ X. Найти плотность распределения вероятностей f(x), математическое ожидание М(X), дисперсию D(X) и вероятность попадания СВ X на отрезок [а; b]. Построить графики функций F(х) и f(x).

3. Решить следующие задачи.
3.1. Валик, изготовлений автоматом, считается стандартным, если отклонение его диаметра от проектного размера не превышает 2 мм. Случайные отклонения диаметров валиков подчиняются нормальному закону со средним квадратичным отклонением 1,6 мм и математическим ожиданием, равным 0. Сколько стандартных валиков (в процентах) изготавливает автомат?

4. Решить следующие задачи.
4.1. Для определения качества производимой заводом продукции отобрано наугад 2500 изделий. Среди них оказалось 50 с дефектами. Частота изготовления бракованных изделий принята за приближенное значение вероятности изготовления бракованного изделия. Определить, с какой вероятностью можно гарантировать, что допущенная при этом абсолютная погрешность не будет превышать 0,02.
Готовые решения данных задач

Вариант 2
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)

1.2. Производят три выстрела по мишени. Вероятность поражения мишени первым выстрелом равна 0,4, вторым – 0,5, третьим – 0,6; СВ X – число поражений мишени.

3. Решить следующие задачи.
3.2. При определении расстояния радиолокатором случайные ошибки распределяются по нормальному закону. Какова вероятность того, что ошибка при определении расстояния не превысит 20 м, если известно, что систематических ошибок радиолокатор не допускает, а дисперсия ошибок равна 1370 м2?

4. Решить следующие задачи.
4.2. Дисперсия каждой из 4500 независимых и одинаково распределенных случайных величин равна 5. Найти вероятность того, что среднее арифметическое этих случайных величин отклонится от своего математического ожидания не более чем на 0,04.
Готовые решения данных задач

Вариант 3
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)

1.3. Вероятность безотказной работы в течение гарантийного срока для телевизоров первого типа равна 0,9, второго типа – 0,7, третьего типа – 0,8; СВ X – число телевизоров, проработавших гарантийный срок, среди трех телевизоров разных типов.

3. Решить следующие задачи.
3.3. Все значения равномерно распределенной СВ X лежат на отрезке [2; 8]. Найти вероятность попадания СВ Х в промежуток (3; 5).

4. Решить следующие задачи.
4.3. Случайная величина X является средней арифметической 3200 независимых и одинаково распределенных случайных величин с математическим ожиданием, равным 3, и дисперсией, равной 2. Найти вероятность того, что СВ X примет значение из промежутка (2,95; 3,075).
Готовые решения данных задач

Вариант 4
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)

1.4. Вероятность поражения цели при одном выстреле равна 0,6; СВ X – число поражений цели при четырех выстрелах.

3. Решить следующие задачи.
3.4. СВ X подчинена закону Пуассона с математическим ожиданием, равным 3. Найти вероятность того, что СВ X примет значение, меньшее, чем ее математическое ожидание.

4. Решить следующие задачи.
4.4. В результате медицинского осмотра 900 призывников установлено, что их средняя масса на 1,2 кг больше средней массы призывников за один из предшествующих периодов. Какова вероятность этого отклонения, если среднее квадратичное отклонение массы призывников равно 8 кг?
Готовые решения данных задач

Вариант 5
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)

1.5. Вероятность выпуска прибора, удовлетворяющего требованиям качества, равна 0,9. В контрольной партии – 3 прибора; СВ X – число приборов, удовлетворяющих требованиям качества.

3. Решить следующие задачи.
3.5. Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляются до ближайшего целого деления. Считая, что ошибки измерения распределены равномерно, найти вероятность того, что при отсчете будет сделана ошибка, меньшая 0,04.

4. Решить следующие задачи.
4.5. СВ является средним арифметическим независимых и одинаково распределенных случайных величин, дисперсия каждой из которых равна 5. Сколько нужно взять таких величин, чтобы СВ Х с вероятностью, не меньшей 0,9973, отклонялась от своего математического ожидания не более чем на 0,01?
Готовые решения данных задач

Вариант 6
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)

1.6. Вероятность перевыполнения плана для СУ-1 равна 0,9, для СУ-2 – 0,8, для СУ-3 – 0,7; СВ X – число СУ, перевыполнивших план.

3. Решить следующие задачи.
3.6. Поток заявок, поступающих на телефонную станцию, представляет собой простейший пуассоновский поток. Математическое ожидание числа вызовов за 1 ч равно 30. Найти вероятность того, что за 1 мин поступит не менее двух вызовов.

4. Решить следующие задачи.
4.6. СВ X является средним арифметическим 10000 независимых одинаково распределенных случайных величин, среднее квадратичное отклонение каждой из которых равно 2. Какое максимальное отклонение СВ X от ее математического ожидания можно ожидать с вероятностью, не меньшей 0,9544?
Готовые решения данных задач

Вариант 7
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)

1.7. Вероятность попадания в цель при одном выстреле равна 0,8; СВ X – число попаданий в цель при трех выстрелах.

3. Решить следующие задачи.
3.7. В лотерее разыгрываются мотоцикл, велосипед и одни часы. Найти математическое ожидание выигрыша для лица, имеющего один билет, если общее количество билетов равно 100.

4. Решить следующие задачи.
4.7. Производится выборочный контроль партии электролампочек для определения средней продолжительности их горения. Каким должен быть объем выборки, чтобы с вероятностью, не меньшей 0,9876, можно было утверждать, что средняя продолжительность эксплуатации лампочки по всей партии отклонилась от средней, полученной в выборке, не более чем на 10 ч, если среднее квадратичное отклонение продолжительности эксплуатации лампочки равно 80 ч?
Готовые решения данных задач

Вариант 8
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)

1.8. Вероятность поступления вызова на АТС в течение 1 мин равна 0,4; СВ X— число вызовов, поступивших на АТС за 4 мин.

3. Решить следующие задачи.
3.8. Считается, что изделие – высшего качества, если отклонение его размеров от номинальных не превосходит по абсолютной величине 3,6 мм. Случайные отклонения размера изделия от номинального подчиняются нормальному закону со средним квадратичным отклонением, равным 3 мм. Систематические отклонения отсутствуют. Определить среднее число изделий высшего качества среди 100 изготовленных.

4. Решить следующие задачи.
4.8. Вероятность того, что наугад выбранная деталь окажется бракованной, при каждой проверке одна и та же и равна 0,1. Партия изделий не принимается при обнаружении не менее 10 бракованных изделий. Сколько надо проверить деталей, чтобы с вероятностью 0,6 можно было утверждать, что партия, имеющая 10 % брака, не будет принята?
Готовые решения данных задач

Вариант 9
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)

1.9. Вероятность сдачи данного экзамена для каждого из четырех студентов равна 0,8; СВ X – число студентов, сдавших экзамен.

4. Решить следующие задачи.
4.9. Сколько надо произвести опытов, чтобы с вероятностью 0,9 утверждать, что частота интересующего нас события будет отличаться от вероятности появления этого события, равной 0,4, не более чем на 0,1?
Готовые решения данных задач

Вариант 10
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)

1.10. Вероятность успешной сдачи первого экзамена для данного студента равна 0,9, второго экзамена – 0,8, третьего – 0,7; СВ Х – число сданных экзаменов.

3. Решить следующие задачи.
3.10. СВ X подчинена нормальному закону с математическим ожиданием, равным 0. Вероятность попадания этой СВ в интервал (–1; 1) равна 0,5. Найти среднее квадратичное отклонение и записать нормальный закон.

4. Решить следующие задачи.
4.10. Вероятность появления некоторого события в одном опыте равна 0,6. Какова вероятность того, что это событие появится в большинстве из 60 опытов?
Готовые решения данных задач

Вариант 11
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)

1.11. При установившемся технологическом процессе предприятие выпускает 2/3 своих изделий первым сортом и 1/3 вторым; СВ X – число изделий первого сорта из взятых наугад четырех.

3. Решить следующие задачи.
3.11. Автобусы некоторого маршрута идут строго по расписанию. Интервал движения – 5 мин. Найти вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобус менее 3 мин.

4. Решить следующие задачи.
4.11. Вероятность появления события в одном опыте равна 0,5. Можно ли с вероятностью, большей 0,97, утверждать, что число появлений события в 1000 независимых опытах находится в пределах от 400 до 600?
Готовые решения данных задач

Вариант 12
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)

1.12. Из партии в 20 изделий, среди которых имеется четыре нестандартных, для проверки качества выбраны случайным образом 3 изделия; СВ X – число нестандартных изделий среди проверяемых.

3. Решить следующие задачи.
3.12. Ребро куба х измерено приближенно: 1 ≤ х ≤ 2. Рассматривая ребро куба как СВ X, распределенную равномерно в интервале (1; 2), найти математическое ожидание и дисперсию объема куба.

4. Решить следующие задачи.
4.12. Вероятность положительного исхода отдельного испытания равна 0,8. Оценить вероятность того, что при 100 независимых повторных испытаниях отклонение частоты положительных исходов от вероятности при отдельном испытании по своей абсолютной величине будет меньше 0,05.
Готовые решения данных задач

Вариант 13
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)

1.13. Вероятность приема каждого из четырех радиосигналов равна 0,6; СВ X – число принятых радиосигналов.

4. Решить следующие задачи.
4.13. Вероятность наличия зазубрин на металлических брусках, изготовленных для обточки, равна 0,2. Оценить вероятность того, что в партии из 1000 брусков отклонение числа пригодных брусков от 800 не превышает 5 %.
Готовые решения данных задач

Вариант 14
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)

1.14. В партии из 15 телефонных аппаратов 5 неисправных; СВ X – число неисправных аппаратов среди трех случайным образом отобранных.

3. Решить следующие задачи.
3.14. При работе ЭВМ время от времени возникают сбои. Поток сбоев можно считать простейшим. Среднее число сбоев за сутки равно 1,5. Найти вероятность того, что в течение суток произойдет хотя бы один сбой.

4. Решить следующие задачи.
4.14. По данным ОТК, брак при выпуске деталей составляет 2,5 %. Пользуясь теоремой Бернулли, оценить вероятность того, что при просмотре партии из 8000 деталей будет установлено отклонение от средней доли брака менее 0,005.
Готовые решения данных задач

Вариант 15
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)

1.15. Двое рабочих, выпускающих однотипную продукцию, допускают производство изделий второго сорта с вероятностями, равными соответственно 0,4 и 0,3. У каждого рабочего взято по 2 изделия; СВ X – число изделий второго сорта среди них.

3. Решить следующие задачи.
3.15. Из пункта С ведется стрельба из орудия вдоль прямой СК. Предполагается, что дальность полета распределена нормально с математическим ожиданием 1000 м и средним квадратичным отклонением 5 м. Определить (в процентах), сколько снарядов упадет с перелетом от 5 до 70 м.

4. Решить следующие задачи.
4.15. Вероятность появления события в отдельном испытании равна 0,6. Применив теорему Бернулли, определить число независимых испытаний, начиная с которого вероятность отклонения частоты события от его вероятности по абсолютной величине меньшего 0,1, больше 0,97.
Готовые решения данных задач

Вариант 16
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)

3. Решить следующие задачи.
3.16. СВ X распределена нормально с математическим ожиданием 40 и дисперсией 100. Вычислить вероятность попадания СВ X в интервал (30; 80).

4. Решить следующие задачи.
4.16. Суточный расход воды в населенном пункте является случайной величиной, среднее квадратичное отклонение которой равно 10 000 л. Оценить вероятность того, что расход воды в этом пункте в течение дня отклоняется от математического ожидания по абсолютной величине более чем на 25 000 л.
Готовые решения данных задач

Вариант 17
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)

1.17. Вероятность отказа прибора за время испытания на надежность равна 0,2; СВ X – число приборов, отказавших в работе, среди пяти испытываемых.

3. Решить следующие задачи.
3.17. Трамваи данного маршрута идут с интервалом в 5 мин. Пассажир подходит к трамвайной остановке в некоторый момент времени. Какова вероятность появления пассажира не ранее чем через 1 мин после ухода предыдущего трамвая, но не позднее чем за 2 мин до отхода следующего трамвая?

4. Решить следующие задачи.
4.17. Математическое ожидание количества выпадающих в течение года в данной местности осадков составляет 60 см. Определить вероятность того, что в этой местности осадков выпадет не менее 180 см.
Готовые решения данных задач

Вариант 18
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)

1.18. В первой коробке 10 сальников, из них 2 бракованных, во второй – 16, из них 4 бракованных, в третьей – 12 сальников, из них 3 бракованных; СВ X – число бракованных сальников при условии, что из каждой коробки взято наугад по одному сальнику.

3. Решить следующие задачи.
3.18. Минутная стрелка часов перемещается скачком в конце каждой минуты. Найти вероятность того, что в данное мгновение часы покажут время, которое отличается от истинного не более чем на 20 с.

4. Решить следующие задачи.
4.18. В результате 200 независимых опытов найдены значения СВ Х1, X2, …, X200 причем М(Х) = D(X) = 2. Оценить сверху вероятности того, что абсолютная величина разности между средним арифметическим значений случайной величины ; и математическим ожиданием меньше 0,2.
Готовые решения данных задач

Вариант 19
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)

1.19. Рабочий обслуживает четыре станка. Вероятность выхода из строя в течение смены для первого станка равна 0,6, для второго – 0,5, для третьего – 0,4, для четвертого – 0,5; СВ X – число станков, вышедших из строя за смену.

3. Решить следующие задачи.
3.19. При заданном положении точки разрыва снаряда цель оказывается накрытой пуассоновским полем осколков с плотностью λ = 2,5 осколков/м2. Площадь проекции цели на плоскость, на которой наблюдается осколочное поле, равна 0,8 м2. Каждый осколок, попавший в цель, поражает ее с полной достоверностью. Найти вероятность того, что цель будет поражена.

4. Решить следующие задачи.
4.19. Дисперсия каждой из 2500 независимых СВ не превышает 5. Оценить вероятность того, что отклонение среднего арифметического этих случайных величин от среднего арифметического их математических ожиданий не превысит 0,4.
Готовые решения данных задач

Вариант 20
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)

1.20. Вероятность выигрыша по одному билету лотереи равна 1/6; СВ X – число выигрышных билетов из четырех.

3. Решить следующие задачи.
3.20. Число атак истребителей, которым может подвергнуться бомбардировщик над территорией противника, есть случайная величина, распределенная по закону Пуассона с математическим ожиданием а = 3. Каждая атака с вероятностью 0,4 заканчивается поражением бомбардировщика. Определить вероятность поражения бомбардировщика в результате трех атак.

4. Решить следующие задачи.
4.20. Для определения средней урожайности поля в 10 000 га предполагается взять на выборку по одному квадратному метру с каждого гектара площади и точно подсчитать урожайность с этих квадратных метров. Оценить вероятность того, что средняя выборочная урожайность будет отличаться от истинной средней урожайности на всем массиве не более чем на 0,1 ц, если предположить, что среднее квадратичное отклонение урожайности не превышает 3 ц?
Готовые решения данных задач

Вариант 21
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)

1.21. В первой студенческой группе из 24 человек 4 отличника, во второй из 22 – 3 отличника, в третьей из 24 – 6 отличников и в четвертой из 20 – 2 отличника; СВ X – число отличников, приглашенных на конференцию, при условии, что из каждой группы выделили случайным образом по одному человеку.

3. Решить следующие задачи.
3.21. Производят взвешивание вещества без систематических ошибок. Случайная ошибка взвешивания распределена нормально с математическим ожиданием 20 кг и средним квадратичным отклонением 2 кг. Найти вероятность того, что следующее взвешивание отличается от математического ожидания не более чем на 100 г.

4. Решить следующие задачи.
4.21. Число телевизоров с плоским экраном составляет в среднем 40 % общего их выпуска. Пользуясь неравенством Чебышева, оценить вероятность того, что в партии из 500 телевизоров доля телевизоров с плоским экраном отклоняется от средней не более чем на 0,06.
Готовые решения данных задач

Вариант 22
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)

1.22. Вероятность выхода из строя каждого из трех блоков прибора в течение гарантийного срока равна 0,3; СВ X – число блоков, вышедших из строя в течение гарантийного срока.

3. Решить следующие задачи.
3.22. Диаметр подшипников, изготовленных на заводе, представляет собой случайную величину, распределенную нормально с математическим ожиданием 1,5 см и средним квадратичным отклонением 0,04 см. Найти вероятность того, что размер наугад взятого подшипника колеблется от 1 до 2 см.

4. Решить следующие задачи.
4.22. Принимая вероятность вызревания кукурузного стебля с тремя початками равной 0,75, оценить с помощью неравенства Чебышева вероятность того, что среди 3000 стеблей опытного участка таких стеблей будет от 2190 до 2310 включительно.
Готовые решения данных задач

Вариант 23
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)

1.23. Вероятность того, что деталь с первого автомата удовлетворяет стандарту, равна 0,9, для второго автомата – 0,8, для третьего – 0,7; СВ X – число деталей, удовлетворяющих стандарту, при условии, что с каждого автомата взято наугад по одной детали.

3. Решить следующие задачи.
3.23. Цена деления шкалы амперметра равна 0,1 А. Показания округляют до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка, превышающая 0,04 А.

4. Решить следующие задачи.
4.23. Для определения средней урожайности на участке площадью в 1800 га взято на выборку по 1 м2 с каждого гектара. Известно, что дисперсия урожайности по всему участку не превышает 4,5. Оценить вероятность того, что средняя выборочная урожайность будет отличаться от средней урожайности по всему участку не более чем на 0,25 ц.
Готовые решения данных задач

Вариант 24
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)

1.24. Вероятности поражения цели каждым из трех стрелков равны соответственно 0,7; 0,8; 0,6; СВ X – число поражений цели при условии, что каждый из стрелков сделал по одному выстрелу.

3. Решить следующие задачи.
3.24. Найти дисперсию и среднее квадратичное отклонение СВ X, распределенной равномерно в интервале (2; 10).

4. Решить следующие задачи.
4.24. Среднее значение скорости ветра у земли в данном пункте равно 16 км/ч. Оценить вероятность того, что в этом пункте скорость ветра не будет превышать 80 км/ч.
Готовые решения данных задач

Вариант 25
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)

1.25. Вероятности выхода из строя в течение гарантийного срока каждого из трех узлов прибора равны соответственно 0,2; 0,3; 0,1; СВ X – число узлов, вышедших из строя в течение гарантийного срока.

3. Решить следующие задачи.
3.25. Радиостанция ведет передачу информации в течение 10 мкс. Работа ее происходит при наличии хаотической импульсной помехи, среднее число импульсов которой в секунду составляет 104. Для срыва передачи достаточно попадания одного импульса помехи в период работы станции. Считая, что число импульсов помехи, попадающих в данный интервал времени, распределено по закону Пуассона, найти вероятность срыва передачи информации.

4. Решить следующие задачи.
4.25. Среднее значение расхода воды в населенном пункте составляет 50 000 л/дн. Оценить вероятность того, что в этом населенном пункте расход воды не будет превышать 150 000 л/дн.
Готовые решения данных задач

Вариант 26
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)

1.26. Вероятность попадания мячом в корзину при каждом броске для данного баскетболиста равна 0,4; СВ X – число попадания при четырех бросках.

3. Решить следующие задачи.
3.26. Найти математическое ожидание и дисперсию: а) числа очков, выпавших при одном бросании игральной кости; б) суммы очков, выпавших при бросании двух игральных костей.

4. Решить следующие задачи.
4.26. Математическое ожидание количества выпадающих в течение года в данной местности осадков составляет 55 см. Оценить вероятность того, что в этой местности осадков выпадет более 175 см.
Готовые решения данных задач

Вариант 27
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)

1.27. В партии из 25 изделий 6 бракованных. Для контроля их качества случайным образом отбирают четыре изделия; СВ X – число бракованных изделий среди отобранных.

3. Решить следующие задачи.
3.27. Считается, что отклонение длины изготавливаемых деталей от стандартных является случайной величиной, распределенной по нормальному закону. Зная, что длина стандартной детали 40 см, а среднее квадратичное отклонение 0,4 см, определить, какую точность длины изделия можно гарантировать с вероятностью 0,8.

4. Решить следующие задачи.
4.27. Число солнечных дней в году для данной местности является случайной величиной, математическое ожидание которой равно 75 дням. Оценить вероятность того, что в течение года в этой местности будет более 200 солнечных дней.
Готовые решения данных задач

Вариант 28
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)

1.28. Выход из строя коробки передач происходит по трем основным причинам: поломка зубьев шестерен, недопустимо большие контактные напряжения и излишняя жесткость конструкции. Каждая из причин приводит к поломке коробки передач с одной и той же вероятностью, равной 0,1; СВ X – число причин, приведших к поломке в одном испытании.

3. Решить следующие задачи.
3.28. Рост мужчины является случайной величиной, распределенной по нормальному закону с математическим ожиданием, равным 170 см, и дисперсией, равной 49 см2. Найти вероятность того, что трое наугад выбранных мужчин будут иметь рост от 170 до 175 см.

4. Решить следующие задачи.
4.28. Математическое ожидание отклонения от центра мишени при стрельбе по ней составляет 6 см. Оценить вероятность того, что при стрельбе по круговой мишени радиусом 15 см произойдет попадание в мишень.
Готовые решения данных задач

Вариант 29
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)

1.29. Из 39 приборов, испытываемых на надежность, 5 высшей категории. Наугад взяли 4 прибора; СВ X – число приборов высшей категории среди отобранных.

3. Решить следующие задачи.
3.29. Найти математическое ожидание, дисперсию и среднее квадратичное отклонение СВ X, распределенной равномерно в интервале (8; 14).

4. Решить следующие задачи.
4.29. Среднее квадратичное отклонение ошибки измерения азимута равно 0,5°, а ее математическое ожидание – нулю. Оценить вероятность того, что ошибка среднего арифметического трех независимых измерений не превзойдет 1°.
Готовые решения данных задач

Вариант 30
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)

1.30. Проводятся три независимых измерения исследуемого образца. Вероятность допустить ошибку в каждом измерении равна 0,01; СВ X – число ошибок, допущенных в измерениях.

3. Решить следующие задачи.
3.30. Среди семян риса 0,4 % семян сорняков. Число сорняков в рисе распределено по закону Пуассона. Найти вероятность того, что при случайном отборе 5000 семян будет обнаружено 5 семян сорняков.

4. Решить следующие задачи.
4.30. Среднее квадратичное отклонение каждой из 2134 независимых СВ не превосходит 4. Оценить вероятность того, что отклонение среднего арифметического этих СВ от среднего арифметического их математических ожиданий не превзойдет 0,5.
Готовые решения данных задач

Источник

4.1. Автомобиль должен проехать по улице, на которой установлено четыре независимо работающих светофора. Каждый светофор с интервалом в 2 мин подает красный и зеленый сигналы. Случайная величина ξ – число остановок автомобиля на этой улице.

Для заданной дискретной случайной величины ξ найти:

1) закон распределения;

2) функцию распределения F(х) и построить ее график;

3) математическое ожидание Mξ;

4) дисперсию Dξ;

5) среднее квадратичное отклонение σξ.

Решение

5.1 Дана плотность распределения p(х) случайной величины ξ . Найти:

1) параметр с;

2) функцию распределения F(х) ;

3) математическое ожидание Mξ;

4) дисперсию Dξ;

5) вероятность попадания случайной величины ξ на отрезок [a; b].

р(х) = 0, если х<0, х > 2

р(х) = с·(х²+1) если 0 ≤ х ≤ 2

а = 0, b = 1

Решение

6.1 В результате эксперимента получены данные, записанные в виде статистического ряда. Требуется:

а) найти размах варьирования и построить интервальный вариационный ряд;

б) построить полигон частот, гистограмму относительных частот;

в) вычислить эмпирическую функцию распределения и построить ее график;

г) найти числовые характеристики выборки xв, Dв, σв, S, S²;

д) считая выборку соответствующей нормальному распределению, найти доверительные интервалы для математического ожидания при надежности γ = 0,95;

е) приняв в качестве нулевой гипотезу Н₀: генеральная совокупность, из которой извлечена выборка, имеет нормальное распределение, проверить ее, пользуясь критерием Пирсона при уровне значимости α = 0,05.

4,2   42,8   31,8   38,2   44,8   41,4   35,8   37,2   43,6   32,2
38,2   41   28,4   33,8   35,6   36,2   38,2   31,6   37,6   34,4
32,4   34,6   45   39,8   42,2   30,2   35,4   39,6   29,8   41
35   38,4   37   31,4   28   37,2   42,4   33,6   38,6   35,6
37,6   28,6   34,2   39   32,6   40,6   35,8   46   34,4   30,4
31,2   34,8   42,6   44,2   40,2   29   38,6   36,8   33,4   36,4
32,8   37,4   28,6   36,4   38,2   30,6   43   34,4   45,2   40,8
45,6   35   40,4   31   43,2   36,2   41   28   37,8   33
41,6   33,2   36,6   43,4   34,8   46   42,2   39,6   30,8   36,2
37,8   29,4   39   41,8   31,6   40,4   43,6   36,4   42,4   40,2

Решение

7.1 Из генеральной совокупности извлечена выборка объемом n .

Результаты измерения признаков X и Y выборки приведены в корреляционной таблице. Найти:

а) числовые характеристики выборки;

б) уравнение линейной регрессии y на x .

в) выборочный коэффициент корреляции;

г) на чертеже построить уравнение регрессии Y на X и поле корреляции;

д) при уровне значимости α =0,01 проверить нулевую гипотезу Н0 : r_ген = 0 о равенстве нулю генерального коэффициента корреляции.

x y	1200	2700	4200	6700	8200	9700	11200	12700	n_х
20	4	2	5						11
520			7	5	2				14
1020				9	14	6			29
1520				7	8	6			21
2020					4	5	7		16
2520						3	2	4	9
n_у	4	2	12	21	28	20	9	4	100

Решение

Данная работа готова. Стоимость 400 руб.

Для получения полной работы выбрать меню «заказ»,

код работы КЧ163

или обратиться в ВК: https://vk.com/superfeo

Источник

В Задачах № 1-7 требуется: найти закон распределения указанной случайной
величины X и ее функцию распределения F (x) . Вычислить математическое ожидание M ( X ) , дисперсию D( X ) и среднее квадратическое отклонение  ( X ) . Построить график функции распределения F (x) .

Задача 1. Вероятность выпуска прибора, удовлетворяющего требованиям качества, равна 0,9. В контрольной партии 3 прибора. Случайная величина X – число приборов, удовлетворяющих требованиям качества.

Задача 2. Вероятность выхода из строя каждого из трех блоков прибора в течение гарантийного срока равна 0,3. Случайная величина X – число блоков, вышедших из строя в течение гарантийного срока.

Задача 3. Вероятность попадания в цель при одном выстреле равна 0,8. Случайная величина X – число попаданий в цель при трех выстрелах.

Задача 4. Автомобиль должен проехать по улице, на которой установлено четыре независимо работающих светофора. Каждый светофор с интервалом в 2 мин подает красный и зеленый сигналы. Случайная величина X – число остановок на этой улице.

Задача 5. При установившемся технологическом процессе предприятие выпускает 2/3 своих изделий первым сортом и 1/3 вторым сортом. Случайная величина X – число изделий первого сорта из взятых наугад четырех.

Задача 6. 90% панелей, изготавливаемых на железобетонном заводе – высшего
сорта. Случайная величина X – число панелей высшего сорта из четырех, взятых наугад.

Задача 7. Вероятность выигрыша по одному билету лотереи равна 1/6. Случайная величина X – число выигрышных билетов из четырех.

В Задачах № 8-10 требуется: составить ряд распределения случайной величины
X , построить полигон распределения, найти функцию распределения F (x) , нарисовать ее график, вычислить M ( X ) , D( X ) .

Задача 8. Для лечения больных применяется метод лечения, который с вероятностью 0,75 дает положительный результат. На отделении находится 6 больных, при лечении которых используется данный метод
X – число больных, при лечении которых достигнут положительный результат.

Задача 9. При перевозке повреждается в среднем одна деталь из 12. Отправлена
партия из 6 деталей.

Задача 10. В гараже 6 машин. Вероятность выхода из строя в течение дня
отдельной машины равна 0,1.
Случайная величина X – числа машин в исправном состоянии

Задача 11. Вероятность появления события А в каждом из 12 повторных
испытаний P( A)  0,75 . Определить среднее значение и дисперсию случайной величины
числа появления события A в 12 независимых повторных испытаниях.

Задача 12. Написать закон распределения указанной случайной величины, вычислить среднее значение и дисперсию случайной величины, начертить многоугольник распределения, построить график функции распределения данной случайной величины X .
Монету подбрасывают 9 раз. Случайная величина X – число появления герба в 9 бросаниях монеты.

Тема:	Биномиальное распределение вероятностей
Артикул:	9102766
Дата написания:	02.08.2020

Тип работы:	Задачи
Предмет:	Теория вероятностей и математическая статистика
Количество страниц:	19

Источник