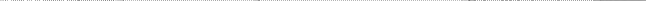17 как изменяется со временем магнитный поток в данной работе

Рис. 5.1. Изменяющийся магнитный поток

1. Запустите эксперимент, щёлкнув мышью по кнопке «Старт». Наблюдайте движение перемычки и изменение магнитного потока Ф (цифры внизу окна).

2. Зацепив мышью, перемещайте движки регуляторов:

L – расстояния между проводами; R – сопротивления перемычки;

B1 – величины индукции магнитного поля.

Зафиксируйте значения, указанные в таблице 5.1 и под ней, для вашей бригады.

				Таблица 5.1
Значения характеристик (не перерисовывать)
Бригады	R , Ом	B1 , мТл	B2 , мТл	B3 , мТл
1 и 5	1	1	40	90
2 и 6	2	2	20	80
3 и 7	1	1	10	70
4 и 8	2	2	-20	100

Для бригад 1–4 L = 1 м, для бригад 5–8 L = 0,7 м.

3. Установив указанное в таблице 5.2 значение скорости движе-ния перемычки, нажмите левую кнопку мыши, когда её маркер раз-мещён над кнопкой «Старт». Значения ЭДС и тока индукции занесите в таблицу 5.2. Повторите измерения для других значений скорости из таблицы 5.2.

		Результаты измерений В = ____ мТл		Таблица 5.2

V , м/c	-10	-8	-6	-4	-2	0	2	4	6	8	10
ЭДС, В
I , мА

4. Повторите измерения для двух других значений индукции магнитного поля, выбирая их из таблицы 5.1. Полученные результаты запишите в таблицы 5.3 и 5.4.

Таблица 5.3

Результаты измерений В = ____ мТл

V , м/c	-10	-8	-6	-4	-2	0	2	4	6	8	10
ЭДС, В
I , мА

		Результаты измерений В = ____ мТл		Таблица 5.4

V , м/c	-10	-8	-6	-4	-2	0	2	4	6	8	10
ЭДС, В
I , мА

Обработка данных и анализ результатов

1. Постройте на одном листе графики зависимости тока индук-ции от скорости движения перемычки при трёх значениях индукции магнитного поля.

2. Для каждой прямой определите тангенс угла наклона по фор-

муле: tg( )ЭКСП	I	.

	V
3. Вычислите теоретическое значение тангенса для каждой пря-
мой по формуле: tg( )ТЕОР	BL .
				R
4. Заполните таблицу 5.4 результатов измерений.
		Результаты измерений	Таблица 5.4

Номер измерения		tg( )ЭКСП, Ac/м	tg( )ТЕОР, Ac/м

5. Сделайте выводы по графикам и результатам измерений.

Контрольные вопросы

1. Что называется элементарным магнитным потоком?

2. Что называется магнитным потоком?

3. При каких условиях магнитный поток равен нулю?

4. При каких условиях магнитный поток равен произведению индукции магнитного поля на площадь контура?

5. Сформулируйте определение явления электромагнитной ин-дукции.

6. Сформулируйте закон электромагнитной индукции.

7. Дайте определение циркуляции магнитного поля.

8. Запишите закон электромагнитной индукции в расшифрован-ном виде.

9. Какое поле является вихревым?

10. Что такое ток Фуко?

11. Чем отличается электрическое поле, созданное точечным за-рядом, от электрического поля, появляющегося при электро-магнитной индукции?

12. Сформулируйте закон электромагнитной индукции для замк-нутого проводящего контура.

13. При каких условиях возникает ЭДС самоиндукции?

14. Сформулируйте определение явления самоиндукции.

15. Сформулируйте словами закон самоиндукции.

16. Назовите все способы создания переменного магнитного по-тока.

17. Как изменяется со временем магнитный поток в данной рабо-те?

18. Как выглядит поверхность, через которую формируется пе-ременный магнитный поток в данной работе?

19. Какова зависимость магнитного потока от времени в данной работе?

20. Как направлен вектор магнитной индукции в данной работе?

Лабораторная работа № 6 СВОБОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ

Выберите «Электричество и магнетизм» и «Свободные колеба-ния в RLC-контуре». Нажмите вверху внутреннего окна кнопку с изо-бражением страницы.

Цель работы:

знакомство с компьютерной моделью процесса свободных за-тухающих колебаний в электрическом колебательном контуре; экспериментальное исследование закономерностей свобод —

ных затухающих колебаний; экспериментальное определение величины индуктивности

контура.

Краткие сведения из теории

Колебательным контуром называется замкнутая цепь, содержа-щая катушку индуктивности с индуктивностью L и конденсатор ём-костью C . Если в цепи нет активного сопротивления R (резистора), то в контуре возможны гармонические (незатухающие) колебания то-ка I , заряда конденсатора q и напряжения на элементах.

Напряжение на конденсаторе Uc Cq .

ЭДС самоиндукции в катушке L dIdt . Напряжение на резисторе U R IR .

Определение тока I dq .

Дифференциальное уравнение свободных незатухающих коле-

баний:

d 2q 02q 0 ,

dt 2

где

– собственная частота контура. Период Т 2 LC .

Решение уравнения свободных незатухающих колебаний имеет

вид:

q(t) q

cos( t ) ,

где – начальная фаза.

Дифференциальное уравнение свободных затухающих колеба-

ний:

d 2q

q 0 ,

dt2

где

– коэффициент затухания.

Решение уравнения свободных затухающих колебаний имеет

вид:

q(t) q e— t cos( t ) ,

где

– частота затухающих колебаний.

Период свободных затухающих колебаний:

Постоянная времени затухания в контуре 1 есть время, за

которое амплитуда колебаний уменьшается в e раз ( e 2,73). Логарифмическим декрементом затухания называется величина,

определяемая формулой ln	q(t)	T T .
q(t T )

Добротность контура равна Q		.

Методика и порядок измерений

Внимательно рассмотрите рисунок 6.1, найдите все регуляторы и другие основные элементы и зарисуйте их в конспект.

Рис. 6.1. Изменяющийся магнитный поток

Нажмите мышью кнопку «Выбор». Подведите маркер мыши к движку регулятора, нажмите на левую кнопку мыши и, удерживая её в нажатом состоянии, меняйте величину ёмкости конденсатора С и установите числовое значение, равное взятому из таблицы 6.1, для вашей бригады. Аналогичным способом установите величину индук-тивности L в соответствии с таблицей 6.1.

Таблица 6.1

Значения ёмкости конденсатора и индуктивности катушки (не перерисовывать)

Бригада	1	2	3	4	5	6	7	8
C , мкФ	3	3	2,7	2,7	2,4	2,4	2	2
L , мГн	6	7	8	9	10	9	8	7

Установите сопротивления резистора R 1 Ом. Нажав кнопку «Старт», наблюдайте график зависимости заряда конденсатора от времени. Измерьте линейкой значения первых шести амплитуд коле-бания заряда A и запишите их в таблицу 6.2. Меняя сопротивление R , повторите измерения амплитуд и заполните таблицу 6.2.

Таблица 6.2

Результаты измерений при С = ___ мкФ, L = ___ мГн, Т = ___ мс

R , Ом	A1 , Кл	A2 , Кл	A3 , Кл	A4 , Кл	A5 , Кл	A6 , Кл	, мс	, с-1

1
2
3
4
5
6
t, мс

Обработка данных и анализ результатов

1. Рассчитайте значения периода колебаний T и запишите в за-головке таблицы 6.2.

2. Рассчитайте время t , при котором измерена соответствующая амплитуда колебания заряда A , и запишите в таблицу 6.2.

3. Постройте на одном чертеже графики экспериментальных за —

висимостей амплитуды колебания заряда А от времени t (6 линий, соответствующих разным R ).

4. Для каждого графика постройте касательную к нему в на-чальный момент времени. Продолжив касательную до пересе-чения с осью времени, определите экспериментальное значе-ние постоянной времени затухания и запишите в таблицу 6.2.

5. Рассчитайте величины коэффициента затухания 1 и также

внесите в таблицу 6.2.

6. Постройте график зависимости коэффициента затухания от сопротивления резистора R .

7. По графику f (R) определите индуктивность контура L ,

используя формулу L 1 R .

8. Запишите ответ и сформулируйте выводы по ответу и графи-кам.

Источник

ЛАБОРАТОРНАЯ РАБОТА

4.2 ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ

Ознакомьтесь с конспектом лекций и
учебником (Савельев, т. 2, §
39–47). Запустите программу. Выберите
«Электричество и магнетизм» и
«Электромагнитная индукция». (Если вы
забыли, как работать с системой
компьютерного моделирования, прочитайте
ВВЕДЕНИЕ с. 5 еще раз.)

Нажмите вверху внутреннего окна кнопку
с изображением страницы. Прочитайте
краткие теоретические сведения.
Необходимое запишите в свой конспект.
Закройте внутреннее окно, нажав кнопку
с крестом справа вверху этого окна.

ЦЕЛЬ РАБОТЫ

Знакомство с моделированием явления
электромагнитной индукции (ЭМИ).
Экспериментальное подтверждение
закономерностей ЭМИ.

КРАТКАЯ ТЕОРИЯ

элементарным
Магнитным потоком dФ_B
через физически малый элемент поверхности
площадью dS называется
скалярное произведение вектора индукции
магнитного поля
на
вектор нормали

к данному элементу поверхности и на
площадь dS:

dФ_B
= ()dS
.

Магнитным потоком
Ф_B через
поверхность площадью S
называется сумма всех элементарных
потоков через все элементы этой
поверхности (интеграл по поверхности):

Ф_B =

.

Анализируя свойства интеграла в правой
части данного соотношения, можем получить
условия, когда для определения потока
не требуется интегрирование.

Простейший вариант: потока нет (Ф_В
= 0), если 1) В = 0, или 2) вектор магнитной
индукции направлен по касательной к
поверхности в любой ее точке ().

Второй вариант: поток есть произведение
индукции на площадь (Ф_В = BS),
если

, то есть одновременно выполняются два
условия: вектор индукции направлен по
нормали и имеет одну и ту же величину в
любой точке поверхности.

ИНДУКЦИЕЙ называется явление возникновения
одного поля (например, электрического)
при изменении другого поля (например,
магнитного).

ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИЕЙ называется
явление возникновения электрического
поля при изменении магнитного поля.

Закон ЭМИ:
циркуляция электрического поля по
замкнутому контуру Г_0Е пропорциональна
быстроте изменения потока магнитного
поля Ф_0В через замкнутую поверхность
S₀ (L₀),
ограниченную контуром L₀
, по которому рассчитана циркуляция.
Математически:

Г_0Е = –
, где знак «–» соответствует «правилу
Ленца» (см. учебник).

В расшифрованном виде
.

В результате ЭМИ возникает электрическое
поле с ненулевой циркуляцией. Поле с
ненулевой циркуляцией называется
вихревым.

Если в таком поле находится проводящее
вещество, то в веществе возникает
вихревой
электрический ток, величина которого
пропорциональна напряженности вихревого
электрического поля. Такие токи называются
токами Фуко.

Если проводящее вещество имеет форму
замкнутого контура,
тогда циркуляция электрического поля
в нем определяет ЭДС, которая в случае
ЭМИ называется ЭДС индукции. Закон ЭМИ
для проводящего контура будет выглядеть
так: ЭДС_ИНД = –.

Ток, который в этом случае появляется
в контуре, называется индукционным.

Обозначая ЭДС индукции символом _инд
и используя закон Ома для полной
цепи, получим выражение для тока индукции:
i_ИНД = _инд
/ R , где R
– сопротивление контура.

Если имеется замкнутый контур с переменным
током, тогда магнитное поле с изменяющимся
потоком создается собственным током в
этом контуре, и в соответствии с законом
ЭМИ в контуре возникает дополнительная
ЭДС, называемая ЭДС самоиндукции.

Явлением САМОИНДУКЦИИ называется
возникновение ЭДС самоиндукции при
протекании по проводнику переменного
тока.

ЗАКОН самоиндукции: ЭДС_{САМОИНД}
= –L
, где L – индуктивность
проводника.

МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ

Закройте окно теории.

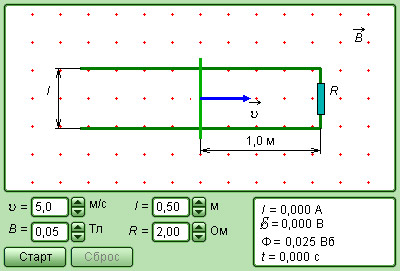
В данной лабораторной работе используется
компьютерная модель, в которой изменяющийся
магнитный поток возникает в результате
движения проводящей перемычки по
параллельным проводникам, замкнутым с
одной стороны.

Эта система изображена на рисунке:

ЗАДАЧА:

Проводящая перемычка движется со
скоростью V по
параллельным проводам, замкнутым с
одной стороны. Система проводников
расположена в однородном магнитном
поле, индукция которого равна В и
направлена перпендикулярно плоскости,
в которой расположены проводники. Найти
ток в перемычке, если ее сопротивление
R, а сопротивлением
проводников можно пренебречь.

Решив задачу в черновике, получите
уравнение для тока в общем виде.

Подготовьте табл. 1, используя образец.
Подготовьте также табл. 3 и 4, аналогичные
табл. 1.

ТАБЛИЦА
1. Результаты измерений
(12 столбцов). В = ____ мТл

ТАБЛИЦА
2. Значения характеристик (не
перерисовывать)

v, м/c
=

–10

–8

…

Бригады

Ом

В₁, мТл

В₂, мТл

В₃, мТл

ЭДС, В

1 и 5

–30

I, мА

2 и 6

–40

3 и 7

–50

4 и 8

–60

–20

100

Для бригад 1–4 L
= 1 м, для бригад 5–8 L
= 0,7 м.

Получите у преподавателя допуск для
выполнения измерений.

ИЗМЕРЕНИЯ:

Закройте окно теории (если вы ее
вызывали), нажав кнопку в правом верхнем
углу внутреннего окна. Запустите
эксперимент, щелкнув мышью по кнопке
«Старт». Наблюдайте движение перемычки
и изменение магнитного потока Ф (цифры
внизу окна).
Зацепив мышью, перемещайте движки
регуляторов

L – расстояния между
проводами,
R – сопротивления
перемычки,
В₁ – величины индукции
магнитного поля,

и зафиксируйте значения, указанные в
табл. 2 и под ней для вашей бригады.

Установив указанное в табл. 1 значение
скорости движения перемычки, нажмите
левую кнопку мыши, когда ее маркер
размещен над кнопкой «Старт». Значения
ЭДС и тока индукции занесите в табл. 1.
Повторите измерения для других значений
скорости из табл. 1.
Повторите измерения для двух других
значений индукции магнитного поля,
выбирая их из табл. 2. Полученные
результаты запишите в табл. 3 и 4.

ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ
ОТЧЕТА

Постройте на одном листе графики
зависимости тока индукции от скорости
движения перемычки при трех значениях
индукции магнитного поля.
Для каждой прямой определите тангенс
угла наклона по формуле

tg()
=
.

Вычислите теоретическое значение
тангенса для каждой прямой по формуле
tg()_ТЕОР
=
.
Заполните таблицу результатов измерений

Номер
измерения

tg()_ЭКСП,
Ac/м

tg()_ТЕОР,
Ac/м
Сделайте выводы по графикам и результатам
измерений.

Вопросы и задания для самоконтроля

Что называется элементарным магнитным
потоком?
Что называется магнитным потоком?
При каких условиях магнитный поток
равен нулю?
При каких условиях магнитный поток
равен произведению индукции магнитного
поля на площадь контура?
Сформулируйте определение явления
электромагнитной индукции.
Сформулируйте закон электромагнитной
индукции.
Дайте определение циркуляции магнитного
поля.
Запишите закон ЭМИ в расшифрованном
виде.
Какое поле является вихревым?
Что такое ток Фуко?
Чем отличается электрическое поле,
созданное точечным зарядом, от
электрического поля, появляющегося
при ЭМИ?
Сформулируйте закон ЭМИ для замкнутого
проводящего контура.
При каких условиях возникает ЭДС
самоиндукции?
Сформулируйте определение явления
самоиндукции.
Сформулируйте словами закон самоиндукции.
Назовите все способы создания переменного
магнитного потока.
Как изменяется со временем магнитный
поток в данной работе?
Как выглядит поверхность, через которую
формируется переменный магнитный поток
в данной работе?
Какова зависимость магнитного потока
от времени в данной работе?
Как направлен вектор магнитной индукции
в данной работе?

Источник

Явление электромагнитной индукции заключается в том, что в результате изменения во времени магнитного потока, который пронизывает замкнутый проводящий контур, в контуре возникает электрический ток. Открыто это явление было физиком из Великобритании Максом Фарадеем в 1831 году.

Формула магнитного потока

Введем обозначения, необходимые нам для записи формулы. Для обозначения магнитного потока используем букву Ф, площади контура – S, модуля вектора магнитной индукции – B, α – это угол между вектором B→ и нормалью n→ к плоскости контура.

Магнитный поток, который проходит через площадь замкнутого проводящего контура, можно задать следующей формулой:

Φ=B·S·cos α,

Проиллюстрируем формулу.

Рисунок 1.20.1. Магнитный поток через замкнутый контур. Направление нормали n→ и выбранное положительное направление l→ обхода контура связаны правилом правого буравчика.

За единицу магнитного потока в СИ принят 1 вебер (Вб). Магнитный поток, равный 1 Вб, может быть создан в плоском контуре площадью 1 м2 под воздействием магнитного поля с индукцией 1 Тл, которое пронизывает контур по направлению нормали.

1 Вб=1 Тл·м2

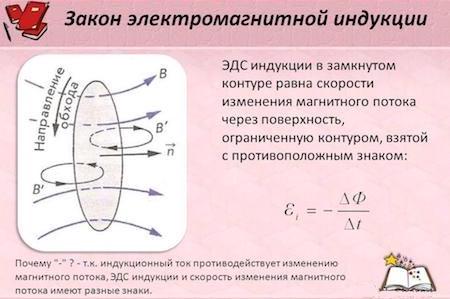
Закон Фарадея

Изменение магнитного потока приводит к тому, что в проводящем контуре возникает ЭДС индукции δинд. Она равна скорости, с которой происходит изменение магнитного потока через ограниченную контуром поверхность, взятой со знаком минус. Впервые экспериментально установил это Макс Фарадей. Он же записал свое наблюдение в виде формулы ЭДС индукции, которая теперь носит название Закона Фарадея:

Определение 1

Закон Фарадея:

δинд=-∆Φ∆t

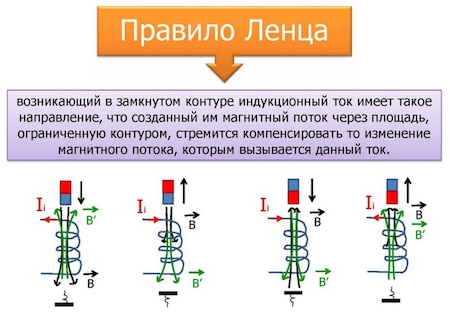
Правило Ленца

Определение 2

Согласно результатам опытов, индукционный ток, который возникает в замкнутом контуре в результате изменения магнитного потока, всегда направлен определенным образом. Создаваемое индукционным током магнитное поле препятствует изменению вызвавшего этот индукционный ток магнитного потока. Ленц сформулировал это правило в 1833 году.

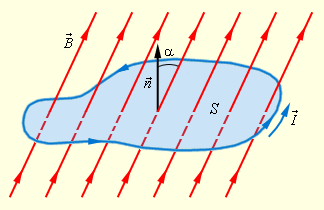
Проиллюстрируем правило Ленца рисунком, на котором изображен неподвижный замкнутый проводящий контур, помещенный в однородное магнитное поле. Модуль индукции увеличивается во времени.

Пример 1

Рисунок 1.20.2. Правило Ленца

Здесь ∆Φ∆t>0, а δинд<0 < 0. Индукционный ток Iинд протекает навстречу выбранному положительному направлению l→ обхода контура.

Благодаря правилу Ленца мы можем обосновать тот факт, что в формуле электромагнитной индукции δинд и ∆Φ∆t противоположны по знакам.

Если задуматься о физическом смысле правила Ленца, то это частный случай Закона сохранения энергии.

Причины возникновения индукционного тока в движущихся и неподвижных проводниках

Причин, по которым может происходить изменение магнитного потока, пронизывающего замкнутый контур, две:

Изменение магнитного потока вследствие перемещения всего контура или отдельных его частей в магнитном поле, которое не изменяется со временем;
Изменение магнитного поля при неподвижном контуре.

Перейдем к рассмотрению этих случаев подробнее.

Перемещение контура или его частей в неизменном магнитном поле

При движении проводников и свободных носителей заряда в магнитном поле возникает ЭДС индукции. Объяснить возникновение δинд можно действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца здесь – это сторонняя сила.

Пример 2

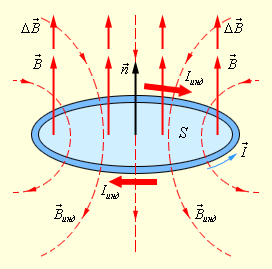
На рисунке мы изобразили пример индукции, когда прямоугольный контур помещен в однородное магнитное поле B→ направленное перпендикулярно плоскости контура. Одна из сторон контура перемещается по двум другим сторонам с некоторой скоростью.

Рисунок 1.20.3. Возникновение ЭДС индукции в движущемся проводнике. Отражена составляющая силы Лоренца, которая действует на свободный электрон

На свободные заряды подвижной части контура воздействует сила Лоренца. Основная составляющая силы Лоренца в данном случае направлена вдоль проводника и связана с переносной скоростью зарядов υ→. Модуль этой сторонней силы равен:

FЛ=eυ→B.

Работа силы FЛ на пути l равна:

A=FЛ·l=eυBl.

По определению ЭДС:

δинд=Ae=υBl.

Значение сторонней силы для неподвижных частей контура равно нулю. Для соотношения δинд можно записать другой вариант формулы. Площадь контура с течением времени изменяется на ΔS=lυΔt. Соответственно, магнитный поток тоже будет с течением времени изменяться: ΔΦ=BlυΔt.

Следовательно,

δинд=∆Φ∆t.

Знаки в формуле, которая связывает δинд и ∆Φ∆t, можно установить в зависимости от того, какие направления нормали и направления контура будут выбраны. В случае выбора согласованных между собой по правилу правого буравчика направлений нормали n→ и положительного направления обхода контура l→ можно прийти к формуле Фарадея.

При условии, что сопротивление всей цепи – это R, то по ней будет протекать индукционный ток, который равен Iинд=δиндR. За время Δt на сопротивлении R выделится джоулево тепло:

∆Q=RIинд2∆t=υ2B2l2R∆t

Парадокса здесь нет. Мы просто не учли воздействие на систему еще одной силы. Объяснение заключается в том, что при протекании индукционного тока по проводнику, расположенному в магнитном поле, на свободные заряды действует еще одна составляющая силы Лоренца, которая связана с относительной скоростью движения зарядов вдоль проводника. Благодаря этой составляющей появляется сила Ампера FА→.

Для рассмотренного выше примера модуль силы Ампера равен FA =IBl. Направление силы Ампера таково, что она совершает отрицательную механическую работу Aмех. Вычислить эту механическую работу за определенный период времени можно по формуле:

Aмех=-Fυ∆t=-IBlυ∆t=-υ2B2l2R∆t

Проводник, перемещающийся в магнитном поле, испытывает магнитное торможение. Это приводит к тому, что полная работа силы Лоренца равна нулю. Джоулево тепло может выделяться либо за счет уменьшения кинетической энергии движущегося проводника, либо за счет энергии, которая поддерживает скорость перемещения проводника в пространстве.

Изменение магнитного поля при неподвижном контуре

Определение 3

Вихревое электрическое поле – это электрическое поле, которое вызывается изменяющимся магнитным полем.

В отличие от потенциального электрического поля работа вихревого электрического поля при перемещении единичного положительного заряда по замкнутому проводящему контуру равна δинд в неподвижном проводнике.

В неподвижном проводнике электроны могут приводиться в движение только под действием электрического поля. А возникновение δинд нельзя объяснить действием силы Лоренца.

Первым, кто ввел понятие вихревого электрического поля, был английский физик Джон Максвелл. Случилось это в 1861 году.

Фактически, явления индукции в подвижных и неподвижных проводниках протекают одинаково. Так что в этом случае мы тоже можем использовать формулу Фарадея. Отличия касаются физической причины возникновения индукционного тока: в движущихся проводниках δинд обусловлена силой Лоренца, в неподвижных – действием на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

Рисунок 1.20.4. Модель электромагнитной индукции

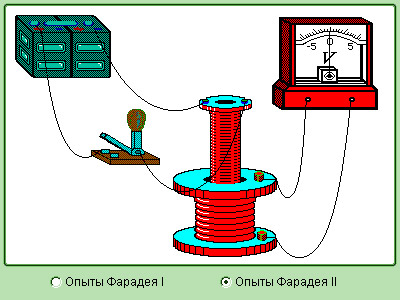
Рисунок 1.20.5. Модель опытов Фарадея

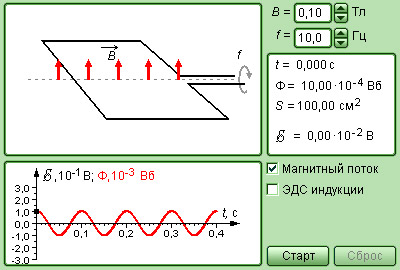
Рисунок 1.20.6. Модель генератора переменного тока

Источник

Взаимосвязь электрических и магнитных полей замечена очень давно. Данную связь еще в 19 веке обнаружил английский ученый-физик Фарадей и дал ему название электромагнитной индукции. Она появляется в тот момент, когда магнитный поток пронизывает поверхность замкнутого контура. После того как происходит изменение магнитного потока в течение определенного времени, в этом контуре наблюдается появление электрического тока.

Взаимосвязь электромагнитной индукции и магнитного потока

Суть магнитного потока отображается известной формулой: Ф = BS cos α. В ней Ф является магнитным потоком, S – поверхность контура (площадь), В – вектор магнитной индукции. Угол α образуется за счет направления вектора магнитной индукции и нормали к поверхности контура. Отсюда следует, что максимального порога магнитный поток достигнет при cos α = 1, а минимального – при cos α = 0.

Во втором варианте вектор В будет перпендикулярен к нормали. Получается, что линии потока не пересекают контур, а лишь скользят по его плоскости. Следовательно, определять характеристики будут линии вектора В, пересекающие поверхность контура. Для расчета в качестве единицы измерения используется вебер: 1 вб = 1в х 1с (вольт-секунда). Еще одной, более мелкой единицей измерения служит максвелл (мкс). Он составляет: 1 вб = 108 мкс, то есть 1 мкс = 10-8 вб.

Для исследования электромагнитной индукции Фарадеем были использованы две проволочные спирали, изолированные между собой и размещенные на катушке из дерева. Одна из них соединялась с источником энергии, а другая – с гальванометром, предназначенным для регистрации малых токов. В тот момент, когда цепь первоначальной спирали замыкалась и размыкалась, в другой цепи стрелка измерительного устройства отклонялась.

Проведение исследований явления индукции

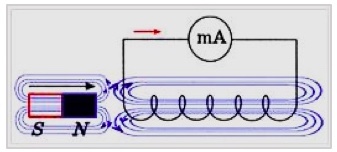
В первой серии опытов Майкл Фарадей вставлял намагниченный металлический брусок в катушку, подключенную к току, а затем вынимал его наружу (рис. 1, 2).

1 2

В случае помещения магнита в катушку, подключенную к измерительному прибору, в цепи начинает протекать индукционный ток. Если магнитный брусок удаляется из катушки, индукционный ток все равно появляется, но его направление становится уже противоположным. Следовательно, параметры индукционного тока будут изменены по направлению движения бруска и в зависимости от полюса, которым он помещается в катушку. На силу тока оказывает влияние быстрота перемещения магнита.

Во второй серии опытов подтверждается явление, при котором изменяющийся ток в одной катушке, вызывает индукционный ток в другой катушке (рис. 3, 4, 5). Это происходит в моменты замыкания и размыкания цепи. От того, замыкается или размыкается электрическая цепь, будет зависеть и направление тока. Кроме того, эти действия есть ни что иное, как способы изменения магнитного потока. При замыкании цепи он будет увеличиваться, а при размыкании – уменьшаться, одновременно пронизывая первую катушку.

3 4

В результате опытов было установлено, что возникновение электрического тока внутри замкнутого проводящего контура возможно лишь в том случае, когда они помещаются в переменное магнитное поле. При этом, поток индукции магнитного поля может изменяться во времени любыми способами.

Электрический ток, появляющийся под действием электромагнитной индукции, получил название индукционного, хотя это и не будет током в общепринятом понимании. Когда замкнутый контур оказывается в магнитном поле, происходит генерация ЭДС с точным значением, а не тока, зависящего от разных сопротивлений. Данное явление получило название ЭДС индукции, которую отражает формула: Еинд = — ∆Ф/∆t. Ее значение совпадает с быстротой изменений магнитного потока, пронизывающего поверхность замкнутого контура, взятого с отрицательным значением. Минус, присутствующий в данном выражении, является отражением правила Ленца.

Правило Ленца в отношении магнитного потока

Известное правило было выведено после проведения цикла исследований в 30-х годах 19 века. Оно сформулировано в следующем виде:

Направление индукционного тока, возбуждаемого в замкнутом контуре изменяющимся магнитным потоком, оказывает влияние на создаваемое им магнитное поле таким образом, что оно в свою очередь создает препятствие магнитному потоку, вызывающему появление индукционного тока.

Когда магнитный поток увеличивается, то есть становится Ф > 0, а ЭДС индукции снижается и становится Еинд < 0, в результате этого появляется электроток с такой направленностью, при которой под влиянием его магнитного поля происходит изменение потока в сторону уменьшения при его прохождении через плоскость замкнутого контура.

Если поток снижается, то наступает обратный процесс, когда Ф < 0 и Еинд > 0, то есть действие магнитного поля индукционного тока, происходит увеличение магнитного потока, проходящего через контур.

Физический смысл правила Ленца заключается в отражении закона сохранения энергии, когда при уменьшении одной величины, другая увеличивается, и, наоборот, при увеличении одной величины другая будет уменьшаться. Различные факторы влияют и на ЭДС индукции. При вводе в катушку поочередно сильного и слабого магнита, прибор соответственно будет показывать в первом случае более высокое, а во втором – более низкое значение. То же самое происходит, когда изменяется скорость движения магнита.

На представленном рисунке видно, как определяется направление индукционного тока с применением правила Ленца. Синий цвет соответствует силовым линиям магнитных полей индукционного тока и постоянного магнита. Они расположены в направлении полюсов от севера к югу, которые имеются в каждом магните.

Изменяющийся магнитный поток приводит к возникновению индукционного электрического тока, направление которого вызывает противодействие со стороны его магнитного поля, препятствующее изменениям магнитного потока. В связи с этим, силовые линии магнитного поля катушки направлены в сторону, противоположную силовым линиям постоянного магнита, поскольку его движение происходит в сторону этой катушки.

Для определения направления тока используется правило буравчика с правой резьбой. Он должен ввинчиваться таким образом, чтобы направление его поступательного движения совпадало с направлением индукционных линий катушки. В этом случае направления индукционного тока и вращения рукоятки буравчика будут совпадать.

Источник

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 226 1–20 | 21–40 | 41–60 | 61–80 | 81–100 …

Добавить в вариант

В однородном магнитном поле с индукцией 20 мТл находится плоский контур в виде кольца радиусом 8 см, изготовленный из тонкой проволоки. Сначала контур располагается так, что линии индукции магнитного поля перпендикулярны плоскости кольца. Затем кольцо поворачивают вокруг его диаметра на угол 135°. Найдите модуль изменения потока вектора магнитной индукции через кольцо при таком повороте. Ответ выразите в мкВб и округлите до целого числа.

Плоская квадратная рамка покоится в однородном магнитном поле, линии магнитной индукции которого перпендикулярны её поверхности. В некоторый момент времени рамку начинают равномерно вращать вокруг оси, лежащей в плоскости рамки, делая 20 оборотов в минуту. Через какой минимальный промежуток времени от начала вращения рамки поток, пронизывающий её поверхность, уменьшится в 2 раза? Ответ приведите в секундах.

Кольцо, изготовленное из тонкой медной проволоки постоянного сечения, находится в однородном магнитном поле vecB , линии индукции которого перпендикулярны плоскости кольца. Модуль индукции магнитного поля равномерно уменьшают до нулевого значения, измеряя в ходе этого процесса напряжение U между точками C и D кольца. Во сколько раз уменьшится U, если проводить этот же эксперимент с кольцом втрое меньшего радиуса, не изменяя другие условия опыта?

По проволочной рамке течёт постоянный электрический ток силой 2 А, который создаёт вокруг рамки магнитное поле. Поток вектора магнитной индукции этого поля через контур, ограниченный данной рамкой, равен 0,006 Вб. Чему равна индуктивность этой рамки? Ответ дайте в миллигенри.

В схеме, изображённой на рисунке, ЭДС источника E = 12 В, его внутреннее сопротивление r = 1 Ом, сопротивление резистора R₁ = 10 Ом, сопротивление катушки индуктивности L равно R₂ = 1 Ом. Вначале ключ К замыкают в положение 1, а через длительное время переключают в положение 2. После этого в замкнутой части цепи справа от ключа выделяется количество теплоты Q = 2 Дж. Какой поток Ф вектора магнитной индукции существовал в катушке индуктивности перед переключением ключа в положение 2?

Проводящий стержень равномерно перемещают по горизонтальным рельсам в однородном магнитном поле с индукцией vecB, линии которого направлены вертикально, снизу вверх (см. рис.). Наблюдатель смотрит на рельсы и стержень сверху, резистор сопротивлением R₁ находится слева от наблюдателя. Точка A лежит в плоскости рельсов.

Определите, как направлен относительно наблюдателя (вправо, влево, вверх, вниз, к наблюдателю, от наблюдателя) вектор индукции магнитного поля, создаваемого в точке A вихревым током, который индуцируется в левой части контура. Ответ запишите словом (словами).

Проводящий стержень равномерно перемещают по горизонтальным рельсам в однородном магнитном поле с индукцией vecB, линии которого направлены вертикально, снизу вверх (см. рис.). Наблюдатель смотрит на рельсы и стержень сверху, резистор сопротивлением R₂ находится справа от наблюдателя. Точка A лежит в плоскости рельсов.

Определите, как направлен относительно наблюдателя (вправо, влево, вверх, вниз, к наблюдателю, от наблюдателя) вектор индукции магнитного поля, создаваемого в точке A вихревым током, который индуцируется в правой части контура. Ответ запишите словом (словами).

Какая энергия запасена в катушке индуктивности, если известно, что при протекании через неё тока силой 0,5 А поток, пронизывающий витки её обмотки, равен 6 Вб? Ответ выразите в джоулях.

Проводящий контур находится в однородном магнитном поле. Модуль индукции магнитного поля начинает увеличиваться, в результате чего по контуру начинает протекать электрический ток, направление которого показано на рисунке стрелкой. Куда направлен относительно рисунка (вправо, влево, вверх, вниз, к наблюдателю, от наблюдателя) вектор индукции магнитного поля? Ответ запишите словом (словами).

Проводящий контур находится в однородном магнитном поле. Модуль индукции магнитного поля начинает уменьшаться, в результате чего по контуру начинает протекать электрический ток, направление которого показано на рисунке стрелкой. Куда вначале был направлен относительно рисунка (вправо, влево, вверх, вниз, к наблюдателю, от наблюдателя) вектор индукции магнитного поля? Ответ запишите словом (словами).

На рисунках изображены схемы физических экспериментов. Установите соответствие между этими экспериментами и их целью. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

СХЕМА ЭКСПЕРИМЕНТА

А)  

Б)  

ЕГО ЦЕЛЬ

1)  Наблюдение картины силовых линий постоянного магнита

2)  Измерение зависимости модуля индукции магнитного поля постоянного магнита от расстояния до его полюса

3)  Обнаружение явления электромагнитной индукции

4)  Проверка закона Ома

СХЕМА ЭКСПЕРИМЕНТА

А)  

Б)  

ЕГО ЦЕЛЬ

1)  Наблюдение картины силовых линий постоянного магнита

2)  Измерение зависимости модуля индукции магнитного поля постоянного магнита от расстояния до его полюса

3)  Обнаружение явления электромагнитной индукции

4)  Проверка закона Ома

Из металлической проволоки сделаны две одинаковые рамки. Рамка 1 находится в однородном магнитном поле с индукцией vecB_1 и в начальный момент времени расположена относительно линий магнитной индукции так, как показано на рис. 1. Рамка 2 находится в однородном магнитном поле с индукцией vecB_2, линии магнитной индукции которого направлены так, как показано на рис. 2.

В момент времени t₀  =  0 рамку 1 начинают вращать (направление вращения указано стрелкой), а модуль индукции B₂ начинает изменяться с течением времени t по закону

Установите соответствие между графиками зависимостей физических величин от времени и физическими величинами. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

ГРАФИК ЗАВИСИМОСТИ ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ ОТ ВРЕМЕНИ

А)  

Б)  

ФИЗИЧЕСКАЯ ВЕЛИЧИНА

1)  Магнитный поток, пронизывающий рамку 1.

2)  Магнитный поток, пронизывающий рамку 2.

3)  Модуль ЭДС индукции, возникающей в рамке 1.

4)  Модуль ЭДС индукции, возникающей в рамке 2.

За время Δt = 4 с магнитный поток через площадку, ограниченную проволочной рамкой, равномерно уменьшается от некоторого значения Φ до нуля. При этом в рамке генерируется ЭДС, равная 6 мВ. Определите начальный магнитный поток Φ через рамку. Ответ дайте в мВб.

Источник: Демонстрационная версия ЕГЭ−2019 по физике

Проволочное кольцо находится в однородном магнитном поле, линии индукции которого перпендикулярны плоскости кольца. Модуль индукции магнитного поля увеличивают с постоянной скоростью. Затем кольцо заменяют на другое, вдвое меньшей площади, сохраняя прежнее расположение кольца относительно линий индукции. При этом скорость изменения модуля индукции магнитного поля увеличивают в 4 раза. Как в результате этого изменятся следующие физические величины: магнитный поток через контур кольца в момент начала изменения модуля магнитной индукции и ЭДС индукции, возникающая в кольце.

Для каждой величины определите соответствующий характер изменения:

1)  увеличится

2)  уменьшится

3)  не изменится

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Магнитный поток

через контур

кольца в момент

начала изменения

модуля магнитной индукции

ЭДС индукции,

возникающая

в кольце

Катушка № 1 включена в электрическую цепь, состоящую из источника напряжения и реостата. Катушка № 2 помещена внутрь катушки № 1 и замкнута (см. рис.).

Из приведённого ниже списка выберите все правильные утверждения, характеризующих процессы в цепи и катушках при перемещении ползунка реостата вправо.

1)  Магнитный поток, пронизывающий катушку № 2, увеличивается.

2)  Вектор индукции магнитного поля, созданного катушкой № 2, в центре этой катушки направлен от наблюдателя.

3)  Вектор индукции магнитного поля, созданного катушкой № 1, всюду увеличивается.

4)  В катушке № 2 индукционный ток направлен по часовой стрелке.

5)  Сила тока в катушке № 1 увеличивается.

Источник: ЕГЭ по физике. Вариант 114

Проводящая рамка площадью 3 см² может вращаться в однородном магнитном поле с индукцией 0,5 Тл. Сначала рамка располагается относительно линий индукции магнитного поля так, как показано на рисунке (вектор задаёт перпендикуляр к плоскости рамки). В момент времени t = 0 рамку начинают равномерно вращать с частотой 5 Гц. В какой момент времени магнитный поток, пронизывающий рамку, в третий раз станет наибольшим по модулю?

Задания Д9 B15 № 3526

Прямоугольная рамка площадью S вращается в однородном магнитном поле индукции B с частотой nu. Причем ось вращения перпендикулярна вектору магнитной индукции. Как со временем меняется магнитный поток, если в начальный момент времени он был максимальным?

Всего: 226 1–20 | 21–40 | 41–60 | 61–80 | 81–100 …

Источник

Номер измерения	tg()_ЭКСП, Ac/м	tg()_ТЕОР, Ac/м