15 января был выдан полугодовой кредит на развитие бизнеса в таблице представлен график погашения

Образовательный портал для подготовки к экзаменам

Математика профильного уровня

Сайты, меню, вход, новости

Задания

Версия для печати и копирования в MS Word

15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.

Дата	15.01	15.02	15.03	15.04	15.05	15.06	15.07
Долг (в процентах от кредита)	100%	90%	80%	70%	60%	50%	0%

В конце каждого месяца, начиная с января, текущий долг увеличивался на 5%, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?

Спрятать решение

Решение.

Не снижая общности рассуждений, примем начальную сумму кредита за 100 руб. и будем считать, что выплаты производились 10 числа каждого месяца. Составим таблицу выплат:

Дата	14.02	14.03	14.04	14.05	14.06	14.07
Долг, руб.	105	94,5	84	73,5	63	52,5
Выплата, руб.	15	14,5	14	13,5	13	52,5
Остаток долга на день выплаты, руб.	90	80	70	60	50	0
Остаток долга на день выплаты, %	90%	80%	70%	60%	50%	0%

Тем самым, полная сумма выплат равна 15 + 14,5 +14 +13,5 +13 + 52,5 = 122,5 руб., переплата составила 22,5%.

Ответ: 22,5.

Спрятать критерии

Критерии проверки:

Критерии оценивания выполнения задания	Баллы
Обоснованно получен верный ответ	2
Верно построена математическая модель	1
Решение не соответствует ни одному из критериев, перечисленных выше	0
Максимальный балл	2

Источник: Материалы для экспертов ЕГЭ 2016

Источник

Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+

АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 г. (без ограничения срока действия).

ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.

Источник

Экономические
задачи

«Табличное
задание долга или условий начисления процентов»

Работа учитель математики

высшей квалификационной категории

МКОУ «Кумылженская СШ № 1 им. Знаменского
А.Д.»

Пономарёвой Ольги Фёдоровны

1. 15 января
был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график
его погашения.

Дата	15.01	15.02	15.03	15.04	15.05	15.06	15.07
Долг (в % от кредита)	100%	90%	80%	70%	60%	50%	0%

В конце каждого
месяца, начиная с января, текущий долг увеличивается на 5%, а выплаты по
погашению кредита происходили в первой половине каждого месяца, начиная с
февраля. На сколько процентов общая сумма выплат при таких условиях больше
суммы самого кредита?

Решение

Пусть взятый полугодовой
кредит на развитие бизнеса равен S. По условию задачи заполним таблицу:

Прошло месяцев	Долг на 15-е число	Долг в конце месяца	Платёж
0	S	1,05S	0
1	0,9S	0,9•0,05+0,9=0,945S	1,05S‒0,9S=0,15S
2	0,8S	0,8•0,05+0,8=0,84S	0,945S‒0,8S=0,145S
3	0,7S	0,7•0,05+0,7=0,735S	0,84S‒0,7S=0,14S
4	0,6S	0,6•0,05+0,6=0,63S	0,735S‒0,6S=0,135S
5	0,5S	0,5•0,05+0,5=0,525S	0,63S‒0,5S=0,13S
6	0	0	0,525S

Общая сумма платежей составила: 0,15S+0,145S+0,14S+0,135S+0,13S+0,525S=1,225S

Общая
сумма выплат больше суммы самого кредита на 1,225S ‒ 1S = 0,225S или на 22,5%.

Ответ: 22,5%.

2. Лидия
положила некоторую сумму на счёт в банке на полгода. По этому вкладу установлен
«плавающий» процент, то есть число начисленных процентов зависит от числа
полных месяцев нахождения вклада на счёте. В таблице представлены условия
начисления процентов.

Срок вклада	1-2 месяца	3-4 месяца	5-6 месяцев
Годовая ставка в %	6%	18%	12%

На
сколько процентов сумма на счёте Лидии при таких условиях больше суммы,
положенной на счёт, если каждый месяц, за исключением последнего, после
начисления процентов она добавляет на счёт такую сумму, чтобы за месяц вклад
увеличился на 10% от первоначального вклада?

Решение

Решаем по простому проценту. Если первые два месяца по 6%
годовых, то 6:12=0,5% в месяц, следующие два месяца по 18% годовых, то
18:12=1,5% в месяц, следующие два месяца по 12% годовых, то 12:12=1% в месяц.

Если каждый месяц,
за исключением последнего, после начисления процентов Лидия добавляет на счёт
такую сумму, чтобы за месяц вклад увеличился на 10% от первоначального вклада,
то: пусть изначально Лидия внесла S, тогда каждый месяц прибавляется 0,1S.

Заполним таблицу:

Месяц	Сумма на счету к началу предыдущего месяца	% от банка
1	S	0,005S
2	1,1S	0,005 • 1,1S = 0,0055S
3	1,2S	0,015 • 1,2S = 0,018S
4	1,3S	0,015 • 1,3S = 0,0195S
5	1,4S	0,01 • 1,4S = 0,014S
6	1,5S	0,01 • 1,5S = 0,015S

Итого банк начислит: (0,005 + 0,0055 +
0,018 + 0,0195 + 0,014 + 0,015)S = 0,077 S

Данная сумма составит: 0,077 S : S • 100 =
7,7%

На 7,7% сумма на счёте Лидии при таких
условиях больше суммы, положенной на счёт.

Ответ: 7,7%.

3. Оксана
положила некоторую сумму на счёт в банке на полгода. По этому вкладу установлен
«плавающий» процент, то есть число начисленных процентов зависит от числа
полных месяцев нахождения вклада на счёте. В таблице представлены условия
начисления процентов.

Срок вклада	1-2 месяца	3-4 месяца	5-6 месяцев
Годовая ставка в %	12%	15%	18%

На
сколько процентов сумма на счёте Оксаны при таких условиях больше суммы,
положенной на счёт, если каждый месяц, за исключением последнего, после
начисления процентов она добавляет на счёт такую сумму, чтобы за месяц вклад
увеличился на 5% от первоначального вклада?

Решение

Решаем по простому проценту. Если первые два месяца по 12%
годовых, то 12:12=1% в месяц, следующие два месяца по 15% годовых, то
15:12=1,25% в месяц, следующие два месяца по 18% годовых, то 18:12=1,5% в
месяц.

Если каждый месяц,
за исключением последнего, после начисления процентов Оксана добавляет на счёт
такую сумму, чтобы за месяц вклад увеличился на 5% от первоначального вклада,
то: пусть изначально Оксана внесла S, тогда каждый месяц прибавляется 0,05S.

Заполним таблицу:

Месяц	Сумма на счету к началу предыдущего месяца	% от банка
1	S	0,01S
2	1,05S	0,01 • 1,05S = 0,0105S
3	1,1S	0,0125 • 1,1S = 0,01375S
4	1,15S	0,0125 • 1,15S = 0,014375S
5	1,2S	0,015 • 1,2S = 0,018S
6	1,25S	0,015 • 1,25S = 0,01875S

Итого банк начислит: (0,01 + 0,0105 +
0,01375 + 0,014375 + 0,018 + 0,01875)S = 0,085375 S

Данная сумма составит: 0,085375 S : S •
100 = 8,5375%

На 8,5375% сумма на счёте Оксаны при
таких условиях больше суммы, положенной на счёт.

Ответ: 8,5375%.

4. Егор взял
кредит 1 марта 2017 года на сумму S млн. рублей.
Условия его возврата таковы:

– 15
апреля каждого года сумма долга увеличивается на 20% по сравнению с началом
предыдущего года;

– с
1 июня по 1 июля каждого года необходимо выплатить часть долга;

– 1
августа каждого года долг должен составлять часть кредита в соответствии со
следующей таблицей:

Год	2017	2018	2019	2020	2021	2022	2023
Долг (млн.руб.)	S	S – 0,3	S – 0,5	S – 1	S – 1,4	S – 1,7	S – 1,8	…	0,1	0

Начиная
с 2023 года, долг равномерно уменьшается на 100 000 рублей в год.
Определите сумму кредита S, если общая сумма выплат равна 4,72 млн.
рублей.

Решение

Сумму кредита S.

Заполним таблицу:

Год	Долг на 1 августа (млн. руб.)	% за пользованием кредитом (20%) (млн руб.)	Выплата основного долга (млн руб.)	Остаток основного долга (млн руб.)
2017	S	0,2 • S	0,3	S – 0,3
2018	S – 0,3	0,2 • (S – 0,3)	0,2	S – 0,5
2019	S – 0,5	0,2 • (S – 0,5)	0,5	S – 1
2020	S – 1	0,2 • (S – 1)	0,4	S – 1,4
2021	S – 1,4	0,2 • (S – 1,4)	0,3	S – 1,7
2022	S – 1,7	0,2 • (S – 1,7)	0,1	S – 1,8
2023	S – 1,8	0,2 • (S – 1,8)	0,1	S – 1,9
2024	S – 1,9	0,2 • (S – 1,9)	0,1	S – 2
2025	S – 2	0,2 • (S – 2)	0,1	S – 2,1
…	…	…	…	…
2021+к	0,1	0,2 • 0,1	0,1	0

S + 0,2 • (S + (S – 0,3) +
(S – 0,5) +
(S – 1) +
(S – 1,4)) +
0,2 • ((S – 1,7) +
(S – 1,8) +
(S – 1,9) +…+
0,1) = 4,72

Арифметическая
прогрессия: (S – 1,7);
(S – 1,8);
(S – 1,9);…;0,1

а₁= (S – 1,7);
а_k= 0,1;
d = ‒ 0,1

а_k= а₁+
d • (k ‒ 1); S_k= (а₁+ а_k) : 2 • k

k
= (а_k‒ а₁+ d) : d; k = (0,1
+ 1,7 – S – 0,1) : (– 0,1) = 10S – 17;

S_k= (S – 1,7 + 0,1) : 2 • (10S – 17) = (0,5S – 0,8) • (10S
– 17);

S + 0,2 • (5S – 3,2) + 0,2
• (0,5S – 0,8) • (10
S – 17) = 4,72;

выполнив
преобразования, получим квадратное уравнение: S²‒ 1,3S ‒ 2,64 = 0;

умножим
на 50, имеем: 50S²‒ 65S ‒ 132=0;

D = 4225
+ 26400 = 30625,

S₁= (65 ‒ 175) : 100 = ‒1,1; S₁<0;

S₂= (65 + 175) : 100 = 2,4; S₂>0.

Сумму
кредита 2,4 млн. руб.

Ответ: 2,4 млн.
руб.

Источник

Задачи ЕГЭ №15 на кредиты обычно относятся к одному из двух характерных типов, которые легко различить между собой.

1 тип. Выплаты кредита производятся равными платежами. Эта схема еще называется «аннуитет»

2 тип. Выплаты кредита подбираются так, что сумма долга уменьшается равномерно. Это так называемая «схема с дифференцированными платежами».

К первому типу относятся также задачи, в которых есть информация о платежах.

Ко второму типу — задачи, в которых есть информация об изменении суммы долга.

В этой статье — решение задач на кредиты второго типа. Схема 2: с дифференцированными платежами. В условии есть информация об изменении суммы долга.

Если в условии задачи сказано, что сумма долга уменьшается равномерно, или что 15-го числа каждого месяца сумма долга на одну и ту же величину меньше суммы долга на 15-е число предыдущего месяца, или есть информация о том, как именно уменьшается сумма долга, — это задача на кредиты второго типа.

1. 15-го января планируется взять кредит в банке на 19 месяцев. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастёт на по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит. Найдите r.

Ключевая фраза в условии: «15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца». Другими словами, сумма долга уменьшается равномерно. Что это значит?

Если вначале сумма долга равна S, то через месяц (после начисления процентов и первой выплаты) она уменьшилась до $frac{18}{19}S$ .Еще через месяц будет $frac{17}{19}S$ ,затем $frac{16}{19}S$ — и так до нуля.

Пусть $k=1+frac{r}{100}$

Нарисуем схему погашения кредита.

Первая строка в схеме — сумма долга после очередной выплаты.

Вторая строка — сумма долга после начисления процентов. Стрелками показано, как меняется сумма долга. Число платежных периодов n = 19.

Вот клиент берет в кредит сумму . После начисления процентов сумма долга увеличилась в раз и стала равна . После первой выплаты сумма долга уменьшилась на $frac{1}{19}S$ и стала равной $frac{18}{19}S$ . Банк снова начисляет проценты, и теперь сумма долга равна $frac{18}{19}kS$ . Таким образом, первая выплата

$Z{}_{1}=Scdot k-frac{18}{19}S$

Вторая выплата: $Z_2=frac{18}{19}kS-frac{17}{19}S$

vdots

19-я выплата: $Z_{19}=frac{1}{19}kS$

Сумма всех выплат:

$Z=Z_1+Z_2+cdots +Z_{19}=cdots =$

$=left(kS-frac{18}{19}Sright)+left(frac{18}{19}kS-frac{17}{19}Sright)+cdots +frac{1}{19}kS=$

$=kSleft(1+frac{18}{19}+frac{17}{19}+cdots +frac{1}{19}right)-Sleft(frac{18}{19}+frac{17}{19}+cdots +frac{1}{19}right).$

Мы сгруппировали слагаемые и вынесли общие множители за скобку. Видим, что и в первой, и во второй скобке — суммы арифметической прогрессии, у которой $a_1=frac{1}{19}$ и $d=frac{1}{19}.$

В первой скобке — сумма 19 слагаемых, во второй сумма 18 слагаемых.

По формуле сумма арифметической прогрессии, $S_n=frac{a_1+a_n}{2}cdot n.$

$frac{1}{19}+frac{2}{19}+cdots +1=frac{1}{2}left(frac{1}{19}+frac{19}{19}right)cdot 19=10;$

$frac{1}{19}+frac{2}{19}+cdots +frac{18}{19}=frac{1}{2}left(frac{1}{19}+frac{18}{19}right)cdot 18=9;$

Получим, что общая сумма выплат $Z=10kS-9S=10left(1+frac{p}{100}right)S-9S=S+frac{10p}{100}cdot S=S+Pi$ , где — величина переплаты. Эта величина показывает, на сколько общая сумма выплат больше суммы, взятой в кредит.

В нашей задаче

$Pi =frac{10p}{100}cdot S=frac{n+1}{2}cdot frac{p}{100}cdot S.$

Здесь n=19 — количество платежных периодов.

Получим:

$frac{10p}{100}cdot S=frac{30}{100}S;$

p=3.

Обратите внимание. Общая сумма выплат:

, где — величина переплаты, $Pi=Scdot frac{n+1}{2}cdot frac{p}{100}.$

В следующих задачах мы будем (если это возможно) применять удобную формулу для переплаты без вывода. Однако на экзамене вам надо будет ее вывести. Иначе решение могут не засчитать.

2. 15-го января планируется взять кредит в банке на некоторое количество месяцев. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.

На сколько месяцев можно взять кредит, если известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит.

Пусть $k=1+frac{r}{100}.$

По формуле для переплаты при выплате суммы кредита дифференцированными платежами имеем:

$Pi=frac{n+1}{200}rS$

где — искомое число месяцев, а r = 3 — величина платежной ставки в процентах. По условию, переплата равна 0,3S , тогда:

$0,3S=frac{n+1}{2}cdot 0,03S$

откуда n=19.

3. 15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.

Дата	15,01	15,02	15,03	15,04	15,05	15,06	15,07
Долг (в процентах от кредита)	100%	90%	80%	70%	60%	50%	0%

В конце каждого месяца, начиная с января, текущий долг увеличивался на , а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?

В этой задаче (как и в большинстве задач ЕГЭ) мы не сможем применить формулу для величины переплаты. Ведь погашение кредита происходит неравномерно. Первые 5 месяцев долг ежемесячно уменьшается на $frac{1}{10}$ своей величины, а в последний месяц сразу до нуля.

Запишем, чему равна каждая выплата, и найдем сумму всех выплат.

Первая выплата:

Вторая:

Следующие:

Общая сумма выплат

$Z-S=S+4,5cdot 0,05cdot S-S=4,5cdot 0,05S=45cdot frac{5}{1000}S=45cdot frac{5}{10}cdot frac{1}{100}S=22,5cdot frac{1}{100}S=22,5%S$

Pi=Z-S

— переплаты, — общая сумма выплат, — сумма кредита.

Ответ: 22,5%

4. В июле 2016 года планируется взять кредит в размере 6,6 млн. руб. Условия возврата таковы:

— каждый январь долг возрастает на по сравнению с концом предыдущего года.

— с февраля по июнь необходимо выплатить часть долга.

— в июле 2017, 2018 и 2019 годов долг остается равным 6,6 млн. руб.

— суммы выплат 2020 и 2021 годов равны.

Найдите r, если в 2021 году долг будет выплачен полностью и общие выплаты составят 12,6 млн. рублей.

S=6,6 млн.руб

Z=12,6 млн. руб

$k=1+frac{r}{100}$

— ежегодные выплаты 2020 и 2021 годов.

$X=frac{k^2S}{k+1}$

$12,6=3cdot 6,6left(k-1right)+frac{2cdot k^2cdot 6,6}{k+1}$

$126=3cdot 66left(k-1right)+frac{2cdot k^2cdot 66}{k+1}$

$42=66left(k-1right)+frac{44k^2}{k+1}$

$D={21}^2-4cdot 55cdot left(-54right)=12321={111}^2 , Longrightarrow k=frac{132}{110}=frac{12}{10}=frac{120}{100}Longrightarrow r=20%$

Ответ: 20%

В 2018 году появились, пожалуй, самая сложная задачи ЕГЭ такого типа. Вот большая статья о том, что же все-таки было на ЕГЭ-2018:

Разбор задачи №17 («Банковская», или «Экономическая») на ЕГЭ по математике 2018 года.

Подведем итоги. Соберем всё, что узнали о решении задач на кредиты по второй схеме (с дифференцированными платежами) в небольшую таблицу:

Равномерное уменьшение суммы долга (схема с дифференцированными платежами). Применяется также, когда известно, как уменьшается сумма долга.
Пусть – сумма кредита, – количество платежных периодов, – процент по кредиту, начисляемый банком. Коэффициент $k = 1+frac{p}{100}$ показывает, во сколько раз увеличивается сумма долга после начисления процентов.
Схема погашения кредита для платежных периодов. – число платежных периодов. 1 выплата: $Z_1=Scdot k-Scdot frac{n-1}{n}$ 2 выплата: $Z_2= S cdot frac{n-1}{n}cdot k-Scdot frac{n-2}{n}$ n-ная выплата: $Z_n=Scdot frac{1}{n}cdot k$ Сумма всех выплат: $=Scdot kleft (1+frac{n-1}{n}+frac{n-2}{n}+...+frac{1}{n}right )-Sleft ( frac{n-1}{n}+frac{n-2}{n}+...+frac{1}{n} right ).$ Применяем формулу суммы арифметической прогрессии. Общая сумма выплат: $Z= Scdot kcdotfrac{n+1}{2}-Scdotfrac{n-1}{2}=S+Scdotfrac{n+1}{2}cdot frac{p}{100}= S + Pi,$ , где – величина переплаты, $Pi=Scdot frac{n+1}{2}cdot frac{p}{100}.$

Равномерное уменьшение суммы долга (схема с дифференцированными платежами). Применяется также, когда известно, как уменьшается сумма долга.

Пусть

– сумма кредита,

– количество платежных периодов,

– процент по кредиту, начисляемый банком. Коэффициент $k = 1+frac{p}{100}$

показывает, во сколько раз увеличивается сумма долга после начисления процентов.

Схема погашения кредита для

платежных периодов.

– число платежных периодов.

1 выплата: $Z_1=Scdot k-Scdot frac{n-1}{n}$

2 выплата: $Z_2= S cdot frac{n-1}{n}cdot k-Scdot frac{n-2}{n}$

n-ная выплата: $Z_n=Scdot frac{1}{n}cdot k$

Сумма всех выплат:

$=Scdot kleft (1+frac{n-1}{n}+frac{n-2}{n}+...+frac{1}{n}right )-Sleft ( frac{n-1}{n}+frac{n-2}{n}+...+frac{1}{n} right ).$

Применяем формулу суммы арифметической прогрессии. Общая сумма выплат:

$Z= Scdot kcdotfrac{n+1}{2}-Scdotfrac{n-1}{2}=S+Scdotfrac{n+1}{2}cdot frac{p}{100}= S + Pi,$ , где

– величина переплаты,

$Pi=Scdot frac{n+1}{2}cdot frac{p}{100}.$

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Профильный ЕГЭ по математике. Задание № 15. Кредиты. Схема 2: известна информация об изменении суммы долга.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

4 июня 2021

В закладки

Обсудить

Жалоба

Дифференцированные платежи

Работа с заданием 17.

Задачи: zadachi.pdf
ДЗ: dz.pdf

Первое видео автора по теме

№1.

Даша взяла ипотеку 6 000 000 рублей под 12% годовых на 10 лет. Выплаты подбираются так, чтобы долг уменьшался равномерно.

1) сколько всего денег Даша отдаст банку?
2) На сколько процентов больше Даша отдаст банку по сравнению с суммой, взятой в кредит
3) Сколько процентов составляет сумма выплат по сравнению с суммой, взятой в кредит?
4) Можно ли ответить на вопросы
2) и 3) не зная, сколько денег взяли в кредит?
5) Чему равен 3й платеж?
6) Чему равен наименьший платеж? Наибольший?
7) Сколько выплатит Даша за первые 6 лет?

№2 (ЕГЭ 2016)

Сергей взял в банке кредит 1,2 млн рублей на срок 24 месяца. По договору Сергей должен возвращать в банк часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 2%, а затем уменьшается на сумму, уплаченную Сергеем банку в конце месяца. Суммы, выплачиваемые Сергеем, подбираются так, чтобы сумма долга уменьшалась равномерно, т.е. на одну и ту же величину каждый месяц. Какую сумму Сергей вернет банку в течение первого года кредитования?

№3 (ЕГЭ 2016)

Эмиль взял кредит в банке на срок 12 месяцев. По договору Эмиль должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется r % этой суммы и своим ежемесячным платежом Эмиль погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая схема называется «схемой с дифференцированными платежами»). Известно, что общая сумма, выплаченная Эмилем банку за весь срок кредитования, оказалась на 13 % больше, чем сумма, взятая им в кредит. Найдите r.

№4

В июле планируется взять кредит в банке на сумму 18 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы: — каждый январь долг возрастает на 10% по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить часть долга; — в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года. На сколько лет был взят кредит, если общая сумма выплат после полного погашения кредита составила 27 млн рублей?

№5 (ЕГЭ 2017)

15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения

Источник

Критерии проверки и оценка решений заданий №17

вариантов КИМ ЕГЭ-2016

(по материалам ФИПИ для региональных предметных комиссий)

Введение текстовых задач экономического содержания в ЕГЭ-2015 по математике есть, пожалуй, наиболее заметное изменение во всем комплексе заданий КИМ с развёрнутым ответом. Во всех заданиях С1–С5 предыдущих лет условие с самого начала формулировалось в математических терминах и отдельно не предполагало построения какой-либо математической модели (частично этот момент мог присутствовать в некоторых способах решения заданий С5 с параметром). Некоторое исключение составляло задание С6, в котором явно текстовое, сюжетное, условие задачи на начальном этапе решения предполагало некоторый перевод на математический язык. Правда, сами тексты условий чаще всего уже активно использовали математическую терминологию: числа, записанные на доске, делимость, доли и дроби, средние величины и т.п.

В заданиях №17 существенно усилена сюжетная, практико-ориентированная, составляющая условия. Относительно существования (возможностей существования) непосредственных связей этих задач с окружающей нас действительностью можно составить отдельный трактат. Авторы ограничились лишь констатацией двух положений. Во-первых, сами сюжеты не есть прямые цитаты «из жизни», они априорно уже являются некоторыми текстовыми упрощениями, моделями, реально возникающих ситуаций. Во-вторых, эти сюжеты условно можно разделить на два типа, использующих соответственно дискретные модели (проценты, погашения кредитов, …) и непрерывные модели (различные производства, протяженные во времени, объемы продукции, …). Приведем критерии оценивания выполнения заданий №17.

Содержание критерия, задание 17	Баллы
Обоснованно получен верный ответ	3
Верно построена математическая модель, решение сведено к исследованию этой модели, получен неверный ответ из-за вычислительной ошибки ИЛИ получен верный ответ, но решение недостаточно обосновано	2
Верно построена математическая модель и решение сведено к исследованию этой модели, при этом решение может быть не завершено	1
Решение не соответствует ни одному из критериев, перечисленных выше	0
Максимальный балл	3

Несколько подробнее, 1 балл можно выставлять в тех случаях, когда сюжетное условие задачи верно сведено к решению математической (вычислительной, числовой, алгебраической, функциональной, геометрической) задачи. Именно к решению, а не к отдельному равенству, набору уравнений, уравнению, задающему функцию и т.п. Грубо говоря, предъявленный текст должен включать направление, «продолжаемое» до верного решения. Оценка в 2 балла, разумеется, включает в себя условия выставления 1 балла, но существенно ближе к верному решению задачи. Здесь предполагается завершенное, практически полное решение соответствующей математической задачи. Типичные допустимые погрешности здесь – вычислительные ошибки (при наличии всех шагов решения) или недостаточно полные обоснования. Например, при отыскании экстремума решение ограничивается верным нахождением лишь критической точки, без надлежащей её проверки на экстремальность. Кратко, « 2 = 3- ».

Отмечается, что термин «математическая модель», быть может, излишне высокопарен для сравнительно простых задач экономического содержания, предлагаемых на ЕГЭ. Однако, по мнению авторов, он наиболее лаконичен, общеупотребим и достаточно ясен для того, чтобы пытаться отыскать ему адекватную замену. Следует подчеркнуть, что один и тот же сюжет может быть успешно сведен к различным математическим моделям (см. ниже задачу 2) и доведён до верного решения. По этой причине в критериях проверки нигде нет жесткого упоминания о какой-либо конкретной (алгебраической, геометрической, функциональной, …) модели.

Вообще, способов верного решения заданий этого типа никак не меньше, чем для привычных текстовых задач. Возможен и стиль, приближенный к высшей математике, и наивный подход, напоминающий арифметический способ решения текстовых задач, и метод, использующий специфические для математической экономики понятия (целевая функция, симплекс-метод и т.п.).

Примеры решения задач

Задача 1.

1 июня 2013 года Всеволод Ярославович взял в банке 900000 рублей в кредит. Схема выплаты кредита следующая: 1 числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Всеволод Ярославович переводит в банк платеж. На какое минимальное количество месяцев Всеволод Ярославович может взять кредит, чтобы ежемесячные выплаты были не более 300000 рублей?

Решение 1.1. («по-взрослому)

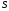
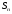
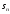
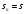
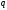
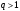
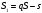
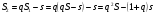
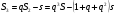
Минимизировать время выплат можно, только максимизировав сами выплаты. Решим задачу в общем виде. Пусть — сумма кредита (в тыс. руб.); — задолженность в — й месяц; — выплата в — й месяц; ; — коэффициент ежемесячного повышения, . Тогда

, , , …

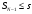
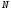
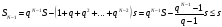
После предпоследней выплаты останется и тогда в последний, -й раз, кредит будет погашен. Значит,

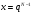
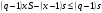
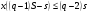
Относительно получаем неравенство

, .

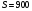
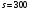
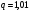
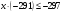
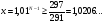
По условию, , , , т.е. , .

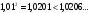
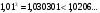
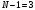
Так как , , то , .

Ответ: 4.

Решение 1.1. («по-детски»)

Если бы банк не брал процентов, то долг можно было бы вернуть за 3 месяца. Банк за 3 месяца возьмет меньше, чем 3% от первоначальной суммы в 900 тыс., т.е. меньше 27 тыс. Поэтому то, что забирает банк, точно можно будет оплатить в 4-й месяц, потратив меньше 300 тыс.

Ответ: 4.

Для следующей задачи ниже предложено три весьма разных способа решения. В первом из них используется метод вспомогательного аргумента, известный из тригонометрии. Второй использует стандартную технику применения производных, а третий основан на традиционном для задач математической экономики использовании так называемого целевого вектора.

Задача 2

Первичная информация разделяется по серверам №1 и №2 и обрабатывается на них. С сервера №1 при объеме Гбайт входящей в него информации выходит Гбайт, а с сервера №2 при объеме Гбайт входящей в него информации выходит Гбайт обработанной информации; . Каков наибольший объем выходящей информации при общем объеме входящей информации в 3364 Гбайт?

Решение 2.1. (алгебра).

Пусть на сервере №1 обрабатывается , а на сервере №2 обрабатывается Гбайт из всей первичной информации. Тогда , а обработано будет Гбайт информации. Требуется найти максимум суммы при условии

, , .

Так как , то , для некоторого угла . Так как , то

для вспомогательного угла с , . Следовательно, наибольшее значение суммы равно . Оно достигается при , , , , т.е. для значений, удовлетворяющих условиям , .

Ответ: 1682.

Решение 2.2. (матем. анализ).

Пусть на сервере №1 обрабатывается , а на сервере №2 обрабатывается Гбайт из всей первичной информации. Тогда , а обработано будет Гбайт информации. Выразим через: . Требуется найти наибольшее значение функции .

, , , , .

— единственная критическая точка и . Условия , выполнены. Если , то , и . Если , то . Поэтому — точка максимума. Значит, .

Ответ: 1682.

Решение 2.3. (геометрия).

Пусть на сервере №1 обрабатывается , а на сервере №2 обрабатывается Гбайт из всей первичной информации. Тогда , а обработано будет Гбайт информации.

Так как , то задает окружность радиуса с центром в начале координат. Проведем целевой вектор и перпендикулярную ему прямую : , проходящую через начало координат. Луч, коллинеарный вектору , пересечет окружность в точке . Прямая , проходящая через точку и перпендикулярная вектору будет касаться окружности и задаваться уравнением : со значением , наибольшим среди всех прямых, параллельных и пересекающих . Условия , для точки выполнены. Значит, .

Ответ: 1682.

Комментарий к условию задачи 2. Ограничение включено для того, чтобы объем выходящей информации был меньше выходящей информации; хватило бы ограничения . Ограничение возникает из-за условий и ; на самом деле . Отсутствие явной ссылки на справедливость неравенств , является тем недочетом, за который вряд ли разумно снижать оценку на 1 балл. Для такого снижения есть более серьезные недостатки. Например, отсутствие обоснования того, что критическая точка есть точка максимума.

Задача 3.

15 – го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.

Дата	15.01	15.02	15.03	15.04	15.05	15.06	15.07
Долг (в процентах от кредита)	100%	90%	80%	70%	60%	50%	0%

Решение. Пусть 15-го числа текущего месяца долг равен , а 15-го числа

предыдущего месяца долг равен . Тогда в конце предыдущего месяца долг равен и поэтому выплата в первой половине текущего месяца равна

Значит, в процентах от суммы кредита выплаты в феврале составили

, в марте составили , в апреле – , в мае –

, в июне – , а в июле . Следовательно, общая сумма выплат составила .

Ответ: 22,5.

Задача 4 (демоверсия)

31 декабря 2013 года Сергей взял в банке 9930000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Сергей переводит в банк определенную сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы Сергей выплатил долг тремя равными ежегодными платежами?

Решение. Пусть сумма кредита равна , ежегодный платеж равен рублей, а годовые составляют %. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент . После первой выплаты сумма долга составит: . После второй выплаты сумма долга составит: .

_{После третьей выплаты сумма долга составит:} .

По условию тремя выплатами Сергей должен погасить кредит полностью, поэтому , откуда При 9930000 и , получаем и рублей.

Ответ: 3993000.

_{Содержание критерия}	_Баллы
_{Обоснованно получен правильный ответ}	₃
_{Получено верное выражение для суммы платежа, но допущена вычислительная ошибка, приведшая к неверному ответу.}	₂
_{Получено выражение для ежегодной выплаты, но уравнение не составлено ИЛИ верный ответ найден подбором}	₁
_{Решение не соответствует ни одному из критериев, перечисленных выше.}	₀
_{Максимальный балл}	₃

Тренировочные задачи

В банк помещена сумма 3900 тысяч рублей под 50% годовых. В конце каждого из первых четырех лет хранения после начисления процентов вкладчик дополнительно вносил на счет одну и ту же фиксированную сумму. К концу пятого года после начисления процентов оказалось, что размер вклада увеличился по сравнению с первоначальным на 725%. Какую сумму вкладчик ежегодно добавлял к вкладу?

Решение. Пусть в банк была помещена сумма тысяч рублей и вкладчик дополнительно вносил ежегодно тысячрублей. Тогда после первого взноса дополнительной суммы вклад составил тысяч рублей, после второго – , после третьего –, после четвертого – .

Получаем уравнение .

. . .

Ответ: 210000.

Транснациональная компания «Amoco inc.» решила произвести недружественное поглощение компании «First Aluminum Company» (FAC) путем скупки акций миноритарных акционеров. Известно, что Amoco inc. было сделано три предложения владельцам акций FAC, при этом цена покупки одной акции каждый раз повышалась на 1/3, а общее количество приобретенных Amoco inc. акций поглощаемой компании увеличивалось на 20%. Определите величину третьего предложения и общее количество скупленных акций FAC, если начальное предложение составило $27 за одну акцию, а количество акций, выкупленных по второй цене, — 15 тысяч.

Решение. Предлагаемая цена покупки составляла соответственно $27; $36; $48. Пусть первоначально было приобретено акций, тогда ; . Итак, было приобретено соответственно 12500 , 15000 и 18000 акций.

Ответ: 48; 45500.

Два брокера купили акции одного достоинства на сумму 3640 р. Когда цена на эти акции возросла, они продали часть акций на сумму 3927 р. Первый брокер продал 75% своих акций, а второй – 80% своих. При этом сумма от продажи акций, полученная вторым брокером, на 140% превысила сумму, полученную первым брокером. На сколько процентов возросла цена одной акции?

Решение. Пусть первоначальная цена одной акции составляларублей и затем она возросла на % и стала составлять рублей. Пусть первый брокер купил акций, а второй – акций.

_{По условию}

_{; ,}

_Ответ:_37,5.

Максим хочет взять кредит 1,5 млн. рублей. Погашаться кредит должен раз в год равными суммами (кроме, может быть, последней) после начисления процентов по ставке 10% годовых. На какое максимальное количество лет может быть взят кредит, чтобы ежегодные выплаты не превосходили 350 тысяч рублей?

Решение.

Год	Долг	Остаток
0	1500000	—
1	1650000	1300000
2	1430000	1080000
3	1188000	838000
4	921800	571800
5	628980	278980
6	306878	—

Ответ: 6 лет.

31 декабря Федор взял в банке кредит 6951000 на три года. Погашаться кредит должен раз в год равными суммами после начисления процентов по ставке 10% годовых. На сколько рублей меньше Федор выплатил банку, если бы кредит был взят на два года?

Решение.

Год	Долг	Остаток
0	p	—
1	1,1p	1,1p-x
2	1,21p-1,1x	1,21p-2,1x
3	1,331p-2,31x	1,331p-3,31x

Ответ: 375100.

Требуется построить несколько одинаковых домов общей площадью . Стоимость дома площадью складываются из стоимости фундамента, пропорциональной и стоимости наземной части, пропорциональной . Известно, что при строительстве дома площадью затрат идет на фундамент. Сколько домов необходимо построить, чтобы общие затраты на строительство были наименьшими?

Алексей приобрёл ценную бумагу за 7000 рублей. Цена бумаги каждый год возрастает на 2000 рублей. В любой момент Алексей может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 10%. В течение какого года после покупки Алексей должен продать ценную бумагу, чтобы через тридцать лет после покупки этой бумаги сумма на банковском счёте была наибольшей?

Решение.

(МГУ. Эконом. ф-т, 1997) Банк планирует вложить на 1 год 40% имеющихся у него средств клиентов в проект , а остальные 60% — в проект . В зависимости от обстоятельств проект может принести прибыль в размере от 19% до 24% годовых, а проект — от 29% до 34% годовых. В конце года банк обязан вернуть деньги клиентам и выплатить им проценты по заранее установленной ставке. Определить наименьший и наибольший возможный уровень процентной ставки по вкладам, при которых чистая прибыль банка составит не менее 10% и не более 15% годовых от суммарных вложений в проекты и .

Решение. Пусть общая сумма вкладов в банк составляет 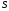рублей, тогда вложения в проекты и равны, соответственно, и . Прибыль от проекта обозначим , от проекта — . По условию, ; . Таким образом, общая прибыль находится в пределах . Чистая прибыль банка находится в пределах от до . Следовательно, возможный уровень процентной ставки по вкладам находится в пределах от 10% до 20% годовых.

Ответ: 10%, 20%.

(ЕГЭ – 26.03.15). Владимир является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно часов в неделю, то за эту неделю они производят единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно часов в неделю, то за эту неделю они производят единиц товара. За каждый час работы (на каждом из заводов) Владимир платит рабочему 500 рублей. Владимиру нужно каждую неделю производить 580 единиц товара. Какую наименьшую сумму придется тратить еженедельно на оплату труда рабочих?

Решение.

Допустим, что на заводе, расположенном в первом городе, рабочие трудятся часов, а на заводе, расположенном во втором городе, часов. Тогда в неделю будет произведено единиц товара, а затраты на оплату труда составят рублей. В этом случае нужно найти наименьшее значение при условии .

Выразим через : ; .

Значит, требуется найти наименьшее значение функции

при .

Для этого найдем производную функции

Найдем точки экстремума:

; ; ,

то есть — единственная точка экстремума, удовлетворяющая условию . Найдем значения функции в найденной точке и на концах отрезка:

, , .

Наименьшее значение равно , значит, наименьшая сумма, которую придется тратить еженедельно на оплату труда рабочих, равна рублей.

Ответ: .

(ЕГЭ – 21.04.15). Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно часов в неделю, то за эту неделю они производят единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно часов в неделю, то за эту неделю они производят единиц товара. За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей. Григорий готов выделить 5000000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?

Решение 1. (матем. анализ)

Допустим, что на заводе, расположенном в первом городе, рабочие трудятся часов, а на заводе, расположенном во втором городе, часов. Тогда в неделю будет произведено

единиц товара, а затраты на оплату труда составят рублей. В этом случае нужно найти наибольшее значение при условии

Выразим через :; ; .

Значит, нам нужно найти наибольшее значение функции

при .

Для этого найдем производную функции :

Найдем точки экстремума:

; ; ; ; ,

, , .

Наибольшее значение равно , значит, наибольшее количество единиц товара равно .

Ответ: .

Решение 2 (векторы)

Рассмотрим векторы ; .

По условию, , следовательно, . .

Согласно векторной форме неравенства Коши-Буняковского .

Следовательно, .

Ответ: .

_{Содержание критерия}	_Баллы
_{Обоснованно получен верный ответ}	₃
_{Верно построена математическая модель, решение сведено к исследованию этой модели и получен результат:} _{— неверный ответ из-за вычислительной ошибки;} _{— верный ответ, но решение недостаточно обосновано}	₂
_{Верно построена математическая модель, решение сведено к исследованию этой модели, при этом решение может быть не завершено}	₁
_{Решение не соответствует ни одному из критериев, перечисленных выше.}	₀
_{Максимальный балл}	₃

(ЕГЭ – 04.06.15). 15 – го января планируется взять кредит в банке на 19 месяцев. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;

— со 2 – го по 14 – е число каждого месяца необходимо выплатить часть долга;

— 15 – го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15 – е число предыдущего месяца.

Известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит. Найдите r.

Решение.

Пусть сумма кредита равна S. По условию, долг перед банком по состоянию на 15 – е число должен уменьшаться равномерно: 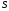, , …., , , 0.

Первого числа каждого месяца долг возрастает на r%. Пусть , тогда последовательность размеров долга на 1 – е число каждого месяца такова:

, , …., , , 0.

Следовательно, выплаты должны быть следующими:

, , … , , .

Всего следует выплатить .

Общая сумма выплат на 30% больше суммы, взятой в кредит, поэтому

; ; .

Ответ: 3.

Второе решение.

Пусть сумма кредита равна S и кредит взят на месяцев. Тогда переплата за кредит равна .

Отсюда ; .

(ЕГЭ – 04.06.15). Зависимость объема Q (в шт) купленного у фирмы товара от цены Р (в руб. за шт.) выражается формулой Q=15000-P, 1000≤P≤15000. Доход от продажи товара составляет PQ рублей. Затраты на производство Q единиц товара составляют 3000Q+5000000 рублей. Прибыль равна разности дохода от продажи товара и затрат на его производство. Стремясь привлечь внимание покупателей, фирма уменьшила цену продукции на 20%, однако ее прибыль не изменилась. На сколько процентов следует увеличить сниженную цену, чтобы добиться наибольшей прибыли?

Решение. Прибыль фирмы выражается как ,

(ЕГЭ – 21.06.15). Строительство нового завода стоит 78 млн. рублей. Затраты на производство тыс. единиц продукции на таком заводе равны млн. рублей в год. Если продукцию завода продать по цене тыс. рублей за единицу, то прибыль фирмы (в млн. рублей) за один год составит . Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении строительство завода окупится не более, чем за 3 года?

Решение. По условию, прибыль за год . Очевидно, прибыль будет наибольшей при . Таким образом, наибольшая прибыль составит или .

, , , , , .

Ответ: 10.

Источник